一类退化加性噪声驱动的随机偏微分方程的振幅方程

雷 婷， 陈光淦

（四川师范大学数学科学学院可视化计算与虚拟现实四川省重点实验室，四川成都610068）

随机偏微分方程在物理、化学等应用学科中具有重要的意义.例如，确定性的Cahn-Hilliard方程描述了材料科学中某些重要的定性特征［1-2］，随机增长模型［3-4］模拟了粗糙非晶体曲面，以及随机Kuramoto-Sivashinsky模型［5-6］刻画了地表侵蚀问题.这些模型都满足本文研究的抽象形式.

本文关心一类含退化噪声的随机偏微分方程

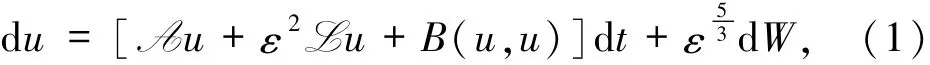
其中算子A、L、B以及扰动参数ε和噪声W的定义详见第一节.

对于方程（1），不同的噪声强度和扰动强度影响着系统最终有效行为.Blömker等研究了随机偏微分方程在扰动强度为0，噪声强度为ε-1［7］；扰动强度为0，噪声强度为情形下的有效行为.本文主要目的是推导出方程（1）的有效逼近系统——振幅方程，给出振幅方程的具体形式以及解逼近的收敛刻画.

1 预备知识

让H表示Hilbert空间，其内积和范数可表示为＜·，·＞和‖·‖.

假设1设A是H空间上自伴随的非正算子，其特征值的相反数满足0≤λ1≤λ2≤…≤λk≤…，并且对所有足够大的k，有λk≥Ckm成立.是特征向量对应的完备正交系，并且Aek＝-λkek.

令N：＝kerA，T：＝N⊥是N在空间H的正交补集，并且Pc：H→N，Ps：＝I-Pc.Ps和Pc与算子A可交换.假设N的维数为n，基为｛e1，e2，…，en｝.任给α∈R，则为H空间上的完备正交基.算子Dα为Dαek＝kαek，所以有‖u‖α＝‖Dαu‖成立.

注记2由假设1定义的算子A生成解析半群｛etA｝t≥0，进一步

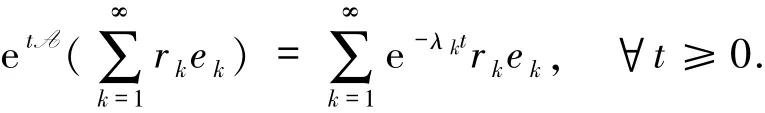
引理3［9］在假设1条件下，存在常数M＞0和K＞0，对任意的t＞0，β≤α和任意的u∈Hβ，满足

假设4（算子L） 固定α∈R，当β∈［0，m），则L：Hα→Hα-β为连续线性映射.一般而言，算子L不与Ps和Pc交换.

假设5（双线性算子B） 设α、β是假设4中的参数，B是从Hα×Hα到Hα-β的有界双线性映射，满足B（u，v）＝B（v，u），并且对任意的u∈N，满足PcB（u，u）＝0.简记符号Bs＝PsB，Bc＝PcB，其中Ps、Pc如前面定义.

为使符号简洁，令F：N→N，对任意的u∈N，有

则F是对称映射F：N3→N，特别地F（u）＝F（u，u，u）.

根据假设，可推出F是三线性的连续算子.因此，F也是有界算子.

引理6［9］非线性算子F满足

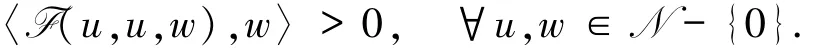
进一步，存在δ＞0，满足

和

设W是抽象完备概率空间（Ω，F，P）上的柱状Wiener过程.W的有界协方差算子为Q：H→H，其中｛αk｝k是一组有界实序列，｛f k｝k∈N是H空间上的一组正交基.

假设7假设

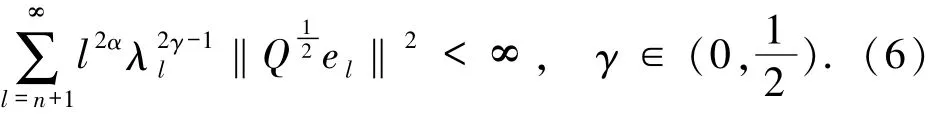
定义8定义随机卷积为

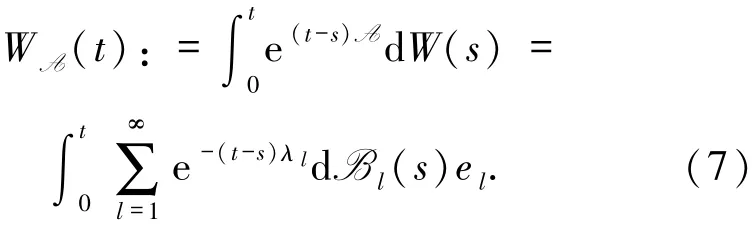
定义9（停时） 对于N×T-值随机过程（a，和时间T0＞0，定义停时

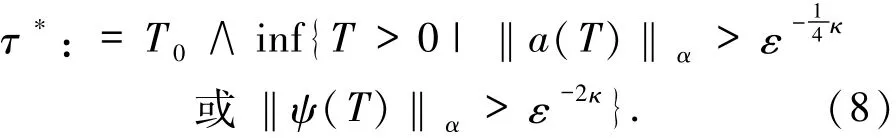
定义10对于实值随机过程构成的集合｛Xε（t）｝t≥0，若对任意的p≥1，存在常数Cp，满足

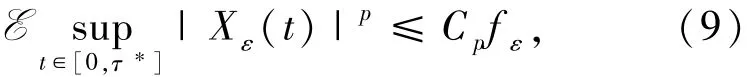
则记Xε＝O（fε），这里fε为无穷小量ε的幂函数，如

本文除特别说明外，C表示所有正的常数.

2 振幅方程

将方程（1）的解u分解为

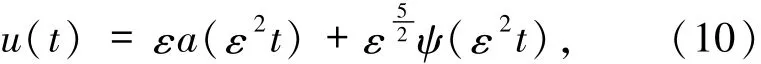
其中a∈N，ψ∈T，时间尺度变换T＝ε2t，则

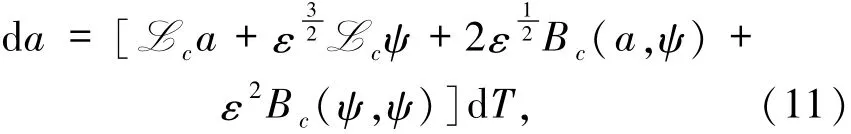
和

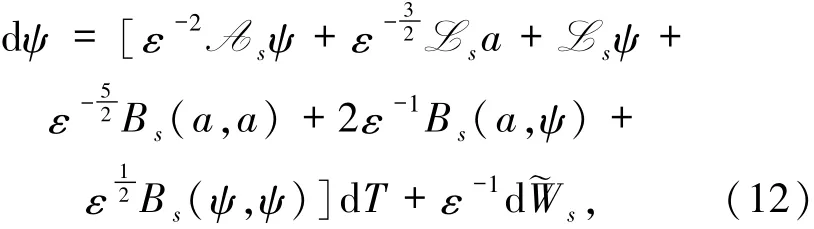
其中˜W（T）：＝εW（ε-2T）是时间尺度变化后的Wiener过程.

对Bc（a，A-1sψ）运用Itô公式，结合（11）和无穷小量ε，得到

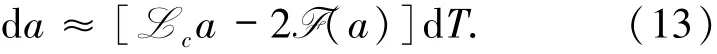
令b：［0，T0］→N是方程

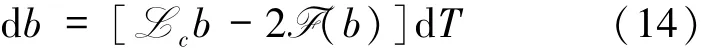
的解，则称方程（14）为方程（1）的振幅方程.当ε充分小时，它将收敛到方程（1）的解.最后将证明方程（1）的解为

若令余项R为

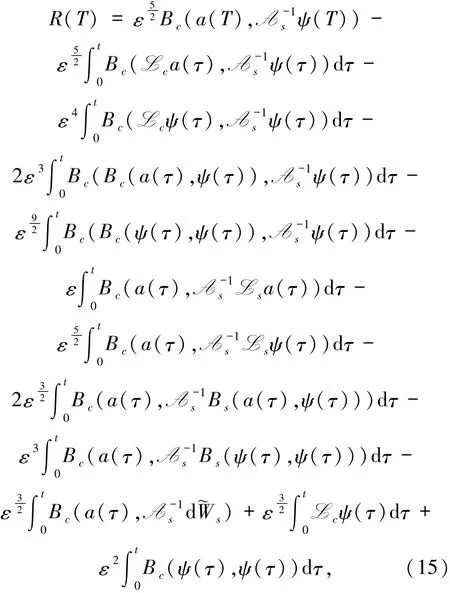
则可得到带余项的振幅方程

3 主要结论和证明

对任意的ε∈（0，1），T≤τ*，

证明考虑方程（12）则T

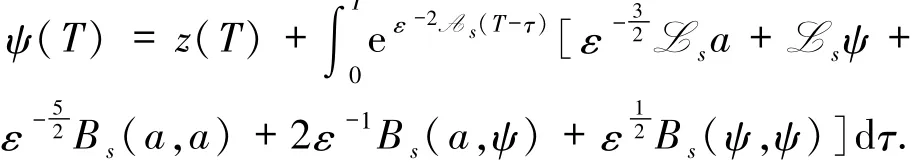
因此可得到

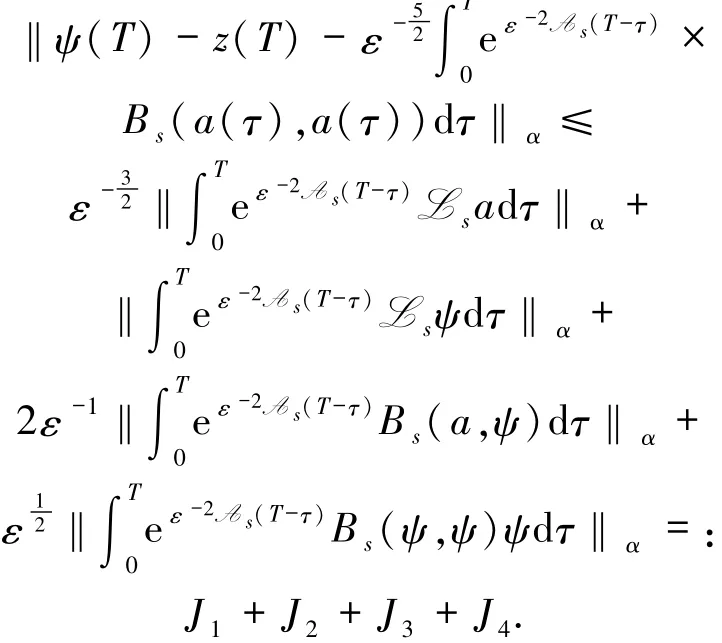
利用引理3，当0≤β＜m时，对任意的T≤τ*，满足

其中利用了τ*的定义和假设4.类似的，对任意的T≤τ*，有

结合4项的结果得到（18）式.

引理12［9］在假设1和7的条件下，‖z（0）‖α＝O（1）.对任意的κ0＞0，p＞1和T＞0，存在常数C＞0，满足

引理13在假设1和5的条件下，利用停时τ*的定义，对任意的ε∈（0，1），则

这套丛书项目由姚安县民族宗教局主持，列入云南省民族宗教委和楚雄州民族宗教委的“民族文化精品工程”。主编郭晓炜具体负责采访、收集、整理和翻译。这项工作从性质上讲，跟老版《梅葛》都属于政府的民族文化工程，但做法上则有很大不同。表现在以下几方面：

证明利用引理3和假设5，当T＜τ*时有进而（20）式得证.

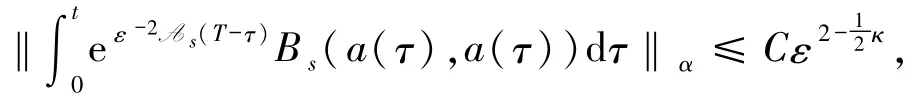
引理14设引理11、12和13成立.对任意的p≥1，存在常数C＞0，满足

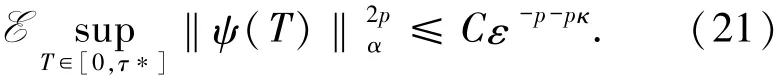
证明由（18）式，运用三角不等式和假设5，得到

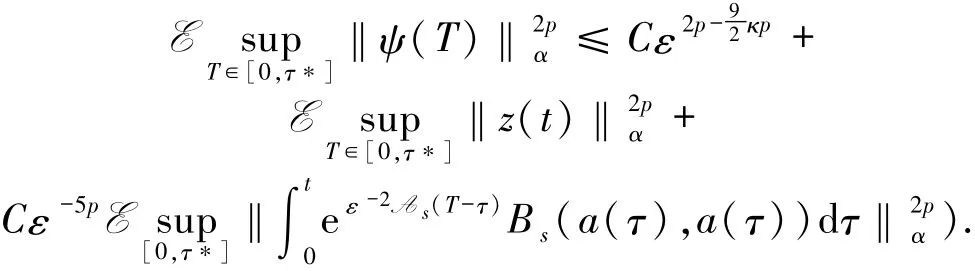
利用引理12和13，（21）式得证.

推论15在引理14的条件下，对任意的p＞1，存在一个常数C＞0，满足

证明由切比雪夫不等式

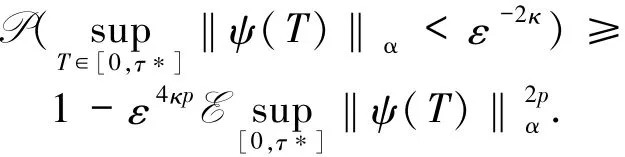
运用（21）式，完成证明.

引理16若假设1、4、5和7成立，对任意的p＞1，存在常数C＞0满足

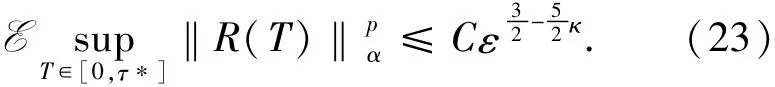
证明对于R的有界性，通过证明（15）式中右端12项各项的有界来说明.这个证明过程依赖假设5和对任意的γ∈R，δ≥0，满足‖ψ‖γ≤C‖ψ‖γ+δ.同时，因为Bc（a（τ），A-1sψ（τ））∈N和A-1s是T⊂Hα空间上的有界线性算子，所以从0到停时τ*的范围内有运用停时τ*的定义，得到

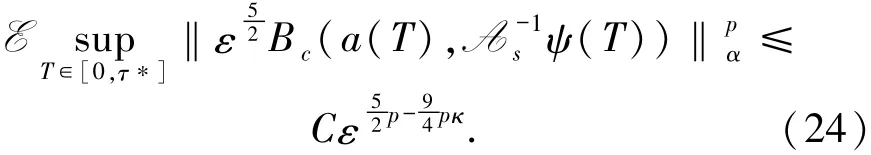
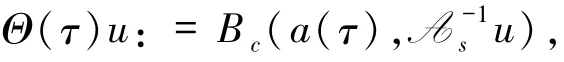
则有

由Burkholder-Davis-Gundy不等式得到

其中｛gk｝k∈N是H空间上的任意正交基，Dα由定义1给出.HS是空间H上的Hilbert-Schmidt算子空间，空间上范数为‖Ψ‖HS＝Tr［ΨΨ*］.因此，

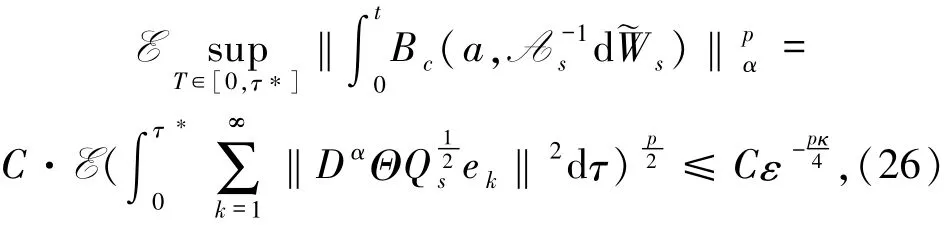
其中

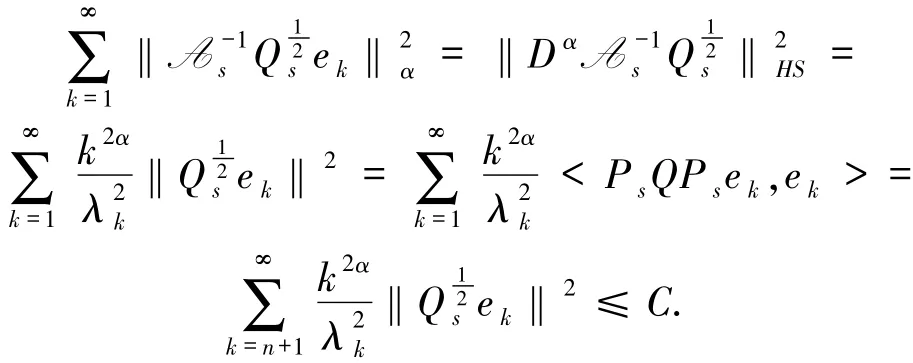
整合R中的12项，又因为在停时的定义中所以可得到结论（23）.

引理17假设1、4、5和7成立.N空间上的随机过程b（T）其初始条件是E‖b（0）‖≤C，t

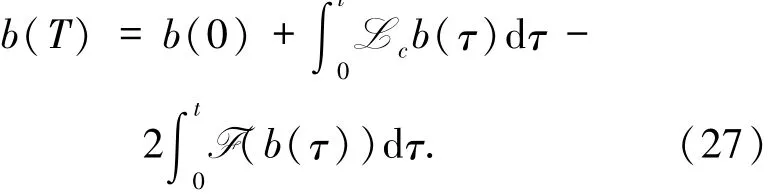
对T0＞0，存在常数C＞O，满足

证明方程（27）解的存在唯一性是成立的.下面验证（28）式，

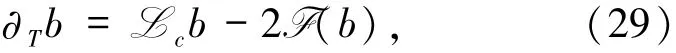
在公式（29）等号两边做内积＜·，b＞，得到利用Young不等式、Cauchy-Schwarz不等式和假设6，得到

忽略4次项，在［0，T］上积分，两边同取次，再取期望，从而得证（28）式.

定义18设空间Ω*⊂Ω，且满足

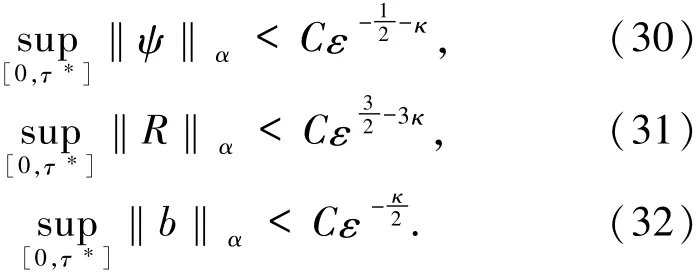
注记19集合Ω*的概率近似于1，因为

运用Chebycher不等式和引理14、16和17，当q充分大时，满足

引理20假设1、4、5、6和7成立.b为（27）式的解.a由（16）式给出定义，在空间Ω*上有若初始条件满足a（0）＝b（0），对上有

和

证明定义φ（T）为

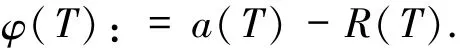
由（18）式得到义h（T）为定

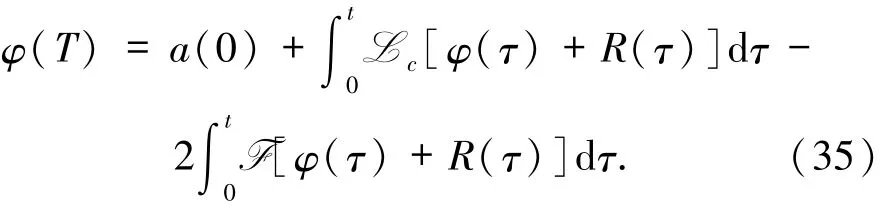
从（35）式中减去（27）式，得到

参见文献［9］引理28，得到在空间Ω*上

运用（31）和（36）式，得到第一部分的结论

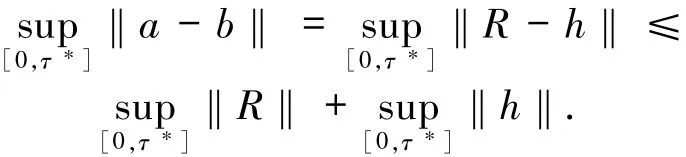
对于定理的第二部分，考虑

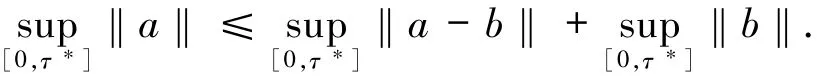
运用第一部分结论和（32）式，得出结论（34）.

定理21（逼近定理） 在假设1、4、5和7的条件下，由公式（10）定义的u为方程（1）的解，其初值条件为其中a（0）和b（0）阶数为1.设b为振幅方程（16）的解.对任意的p＞1和T0＞0，存在常数C＞0，满足

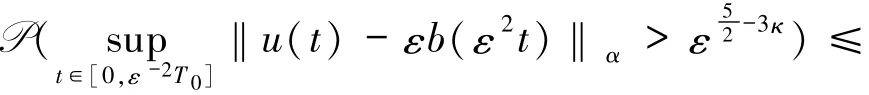
证明对于停时，注意到

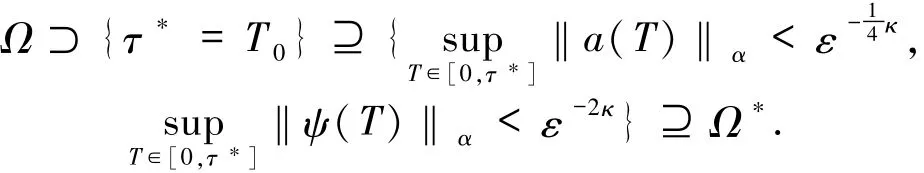
对于逼近结论，运用（11）式和三角不等式，得到

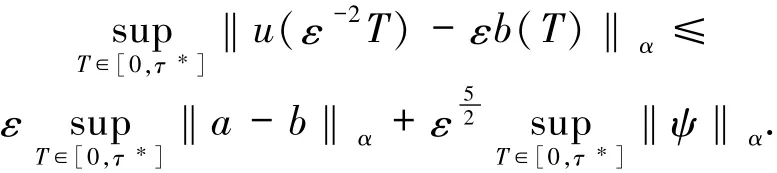
由（30）和（33）式，在空间Ω*上有