粗糙互信息的不平衡多标记特征选择算法

陈 飞，史金成

（铜陵学院数学与计算机学院，安徽铜陵244061）

多标记学习作为一种流行的机器学习方法，得到了众多学者的关注与研究[1-3]。现实世界中也有大量多标记对象，例如一副自然风景图可以标上“蓝天”、“白云”、“沙漠”、“小草”等标记，一篇新闻可以属于“经济”、“文化”和“政治”等。为了尽可能地对样本进行准确标记，就需要对大量特征进行描述。大量的特征虽然会提高描述的准确性，但特征的增多会产生冗余特征或者不相关特征，这些特征会降低分类器的精度，增加算法运行时间。因此降低多标记的特征维数有重要的意义[4]。

目前，特征降维大致有两类方法：特征提取和特征选择。特征提取方法主要是通过特征之间的映射得到一组新的特征子集，但是在映射过程中会改变原始的特征信息，从而丢失一些原始信息，如线性判别分析[5]、依赖度最大化的多标记维数约简[6]等。特征选择方法利用一定的度量关系或评价指标得出一组特征序列或者特征子集，保持了原有特征空间的信息。目前，多数学者利用信息增益（Information Gain,IG）或互信息（Mutual Information,MI）作为评价指标对特征子集进行选择，并提出了多种行之有效的算法[7-9]。

在多标记学习框架之下，标记并不是均匀分布的，有些标记出现的频率高，能描述大部分样本，称之为高密度标记；有些标记出现的频率低，只能描述少部分样本，称之为低密度标记。这些低密度标记往往是由少数特征所决定的，这些特征可能与标记空间整体的相关性不高，但却可能是某些低密度标记的关键特征，如果仅仅考量与标记空间整体的相关性，那么这些特征会被删去从而影响分类器的分类精度。若将标记空间进行划分，考虑部分标记空间甚至单个标记与特征的相关性，无疑会提高算法的有效性。

针对上述问题，本文提出了一种基于粗糙互信息的不平衡多标记特征选择算法，根据标记密度的高低划分标记空间，引入模糊熵修正传统的互信息，并以此来度量特征与标记的相关性，再对不同空间得到的特征序列进行差异性比例的采样，最终将这些特征作为特征子集进行相关训练与测试。

1 多标记学习

1.1 多标记学习框架

在多标记学习中，每个实例样本都同时拥有多个特征和多种标记，学习的目的是将未知的实例对应上尽可能多的正确标记[10]。假设F是由n个特征组成的特征集合F={f1,f2,f3,…,fn}，L是由m个标记组成的标记集合，L={l1,l2,l3,…,lm}，则含有a个样本的多标记数据集可表示成

1.2 粗糙互信息

定义1[11]设论域U、属性P对应的划分为U/P=X={x1,x2,x3,…,xn}，其中xi为等价类，则基于粗糙集等价类所表达的信息量为

其中|*|表示集合元素的基数，并且有0≤I(xi)＜1。

定义2[11]设论域U，属性P对论域U的划分为U/P=X={x1,x2,x3,…,xn}，则P的信息熵为

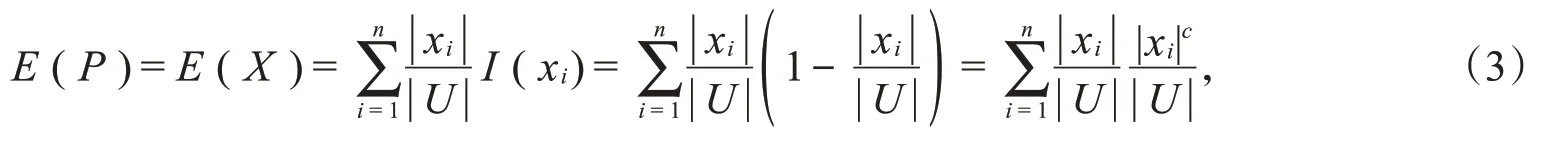
其中c表示求补，并且0≤E(X)＜1-。

定义3[11]设多标记特征空间中某个划分为X={x1,x2,x3,…,xn}，标记空间中划分为Y={y1,y2,y3,…,ym}，根据定义1，可得多标记条件下自信息量为

由特征空间和标记空间联合组成的空间记为

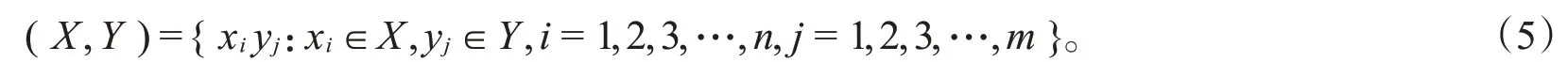
符号集(X,Y)上的条件熵[11]可以定义为

符号集(X,Y)上的每个元素(xi,yj)的联合熵[11]定义为

符号集(X,Y)上的粗糙互信息定义为

由文献[12]可知，粗糙互信息、条件熵和自信息量之间存在着如下关系：

进一步地，通过联合熵能得出如下关系：

式（10）是本文的主要计算公式。

2 粗糙互信息不平衡多标记特征选择算法

在多标记学习框架之下，标记空间中标记并不是均匀分布的。如果仅仅单一考量与标记空间整体的相关性，那么少数低密度标记的关键特征可能会被忽略掉，进而影响分类精度。因此，本文算法将标记空间进行划分，通过对不同标记空间得到的相关性特征序列进行差异化采样，并对采样的特征进行并集运算得出最终的特征子集，以此来进行训练和测试。在有效降低特征维数的前提下，既保留了对标记空间有着强相关的特征，又提高了分类器精度。具体算法步骤如下。

第一步：划分空间。根据每个标记出现的频率从高到低进行排序，前50%的标记划分为高密度空间，后50%的标记划分为低密度空间。

第二步：计算相关性。利用式（10）计算每个标记与特征的相关性，得出每个标记相应的特征序列。

第三步：差异化采样。高密度标记空间中标记取前k1个重要特征，低密度标记空间取前k2个重要特征，k1＞k2。

第四步：对得到的不同特征序列进行并集运算得出最终特征子集。

3 实验设计与结果分析

3.1 实验数据集

为了验证本文算法的有效性，选择了5个公开数据集进行对比实验，相关信息如下页表1所示，实验数据均来自http：//mulan.sourceforge.net/datasets.html。

3.2 评价指标

本文将平均查准率（AveragePrecision,AP），排位缺失（Ranking Loss,RL），海明缺失（Hamming Loss,HL）和单错误（One Error,OE）作为性能评价指标[9]，其中AP值越大表明分类效果越好，RL、HL和OE值则是越小分类效果越好。

3.3 实验结果分析

实验采样3组，采样数目分别是k1=20、k2=15（第1组），k1=30、k2=15（第2组），k1=30、k2=20（第3组）。在5个数据集上的特征选择数目见表2，分类器采用ML-kNN[13]。为了证明算法的有效性，对比了MDDM算法[6]（Multi-label Dimensionality Reduction via Dependence Maximization）和PMU算法[14]（Pairwise Multivariate Mutual Information）。MDDM算法根据映射方法又分为MDDMproj算法和MDDMspc算法。由于MDDM和PMU算法是得到一组特征序列，实验中选取前n个特征作为特征子集，n的取值与k1=30，k2=20特征数目保持一致。分类器ML-kNN的参数值设置为默认参数值。

从表2可以看出，本文算法可以大大减少特征数目，特征选择后的数目均不到原始特征数目的25%，在Rec数据集上更是减少到了原始的13.2%。

表1 数据集基本信息

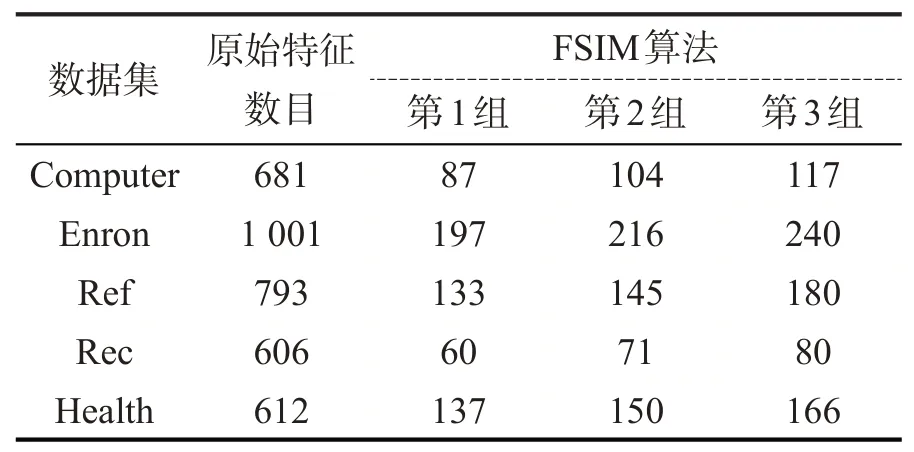
表2 FSIM算法不同采样情况的特征选择数目

表3列出了在4种不同的评价指标下，不同算法的实验结果。“↑”表示指标的取值越大越好，“↓”表示指标的取值越小越好，“Average”行数据表示的是每个算法在当前指标下的平均值，“Original”列数据表示未进行特征选择的实验结果。

表3 不同算法在四种评价指标上的结果

从表3可以看出，在5个数据集的20个结果中，仅有Computer数据集的OE指标劣于未进行特征选择的结果，其余均优于原始结果。同时，本文算法在3组实验中有17个是最优的。在k1=30，k2=20的取值条件下：RL指标中有4个数据集的结果是最优的；在Computer数据集上最优结果也为本算法；AP和HL指标中有3个数据集结果最优；OE指标中，虽然有3个数据集的最优结果不是本文算法，但在Rec和Health数据集中，本文算法在k1=30，k2=20的取值条件下与最优结果的误差不到4%；在Computer数据集中与最优结果更是仅有1%左右的误差。以上实验结果证明了本文算法的有效性。

4 总结

本文提出的基于粗糙互信息的不平衡多标记特征选择算法，用粗糙互信息代替传统互信息减少了计算复杂度，同时考虑到标记的不平衡分布对标记空间进行划分，在不改变标记空间中的标记分布的情况下，对特征进行差异化采样，保证了每个标记的重要特征不丢失。但算法仍存在问题，采样数目是人为设定的，后期将考虑如何自适应采样数目。