先进控制技术在波浪发电系统中的应用*

邱 孟,杨俊华,林汇金,谢子森,黄纬邦

(广东工业大学 自动化学院,广东 广州 510006)

0 引 言

经济的快速发展，化石燃料的生产与运输供应日趋紧张，环境污染严重，因此可持续发展的清洁新能源受到各国重视，部分国家则把发展目标转向了海洋[1]。海洋约占地球面积的71%，到达地球的能量大部分被海洋吸收，转换成波浪、潮汐、温差能等储存在海洋中。其中，波浪能分布广泛、储量丰富，以机械能的形式存在，开发和利用对环境造成的影响较小。但其存在分布不均、随时间地域变化、能量密度较低等问题[2-4]，使波浪能发电较为困难。事实上，波浪随机性会导致发电装置输出电压幅值、相位不稳定，直接影响了并网稳定性，需采用适当的控制策略改善系统输出。虽然波浪发电的关键技术较多，但目前亟需解决的问题主要有2点：最大波浪能跟踪控制和电能质量改善。

众所周知，波浪发电系统具有强非线性，在不同时间和地域呈现强随机性，无法对系统精确建模，难以实现有效控制。将先进电力电子技术、传感技术及先进控制技术引入波浪发电系统控制，可提高波能转换效率及稳定性[5]，已出现了一批有价值的研究结果。如何阐述这些成果，也是一个必须明晰的问题。根据已有相关文献分析，按照控制方法或策略进行分类，可能会更加合理和方便易行。本文介绍了6种先进控制技术在波能转换装置控制方面的应用，并结合控制技术的特点，讨论未来发展方向。

1 波能转换装置控制目标

目前已存在许多不同种类的波能转换装置，其控制方法有所不同，一般来说，波能量转换装置的控制结构图如图1所示。

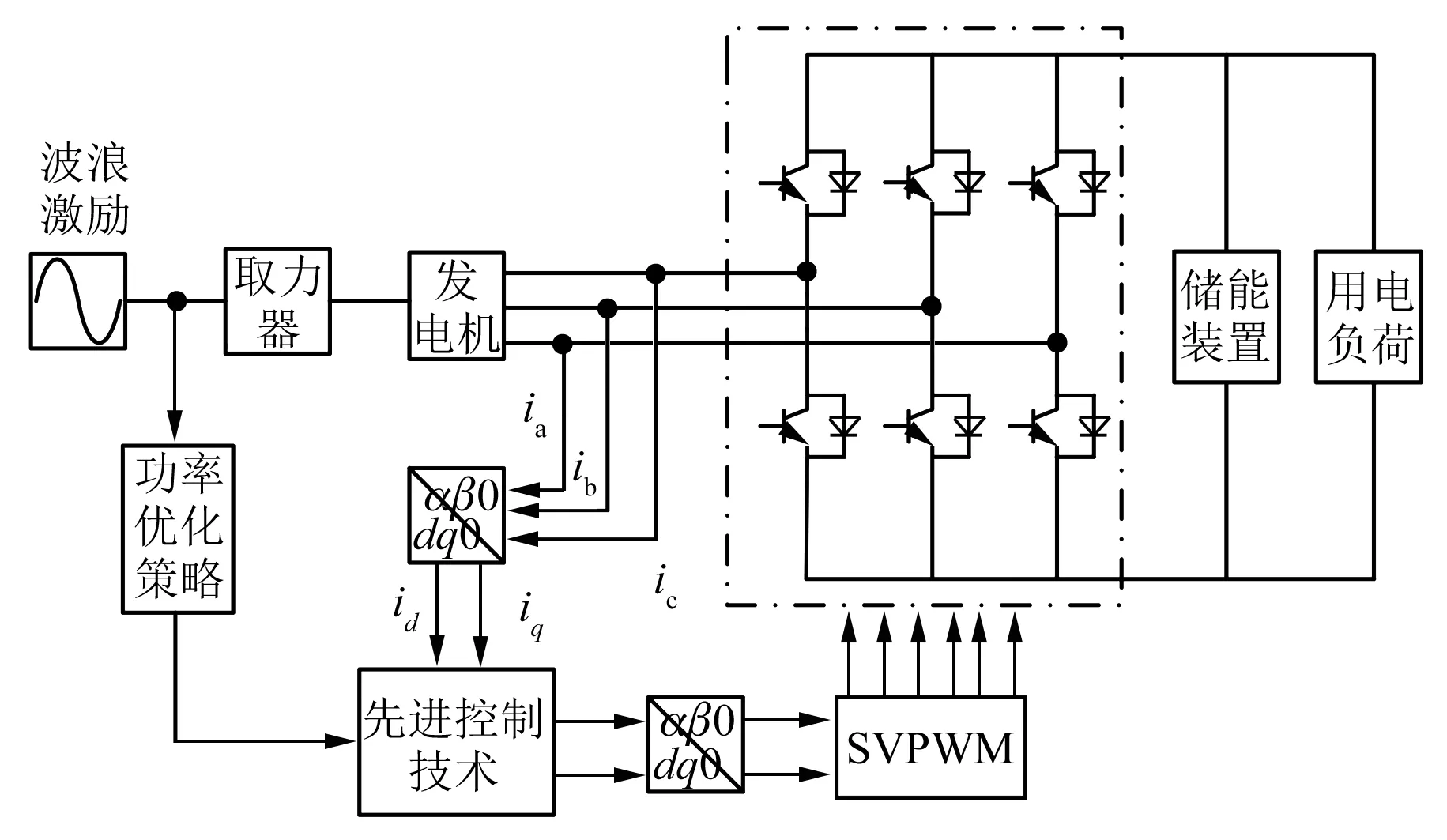
图1 波能转换转置控制结构图

波浪激励作用在与发电机直接相连的取力器(PTO)上，带动发电机运动。波能转换装置对采集到的波浪信息进行功率最优化分析，通过先进控制技术控制整流装置的开断，以此获得期望的电机动子速度和定子电流。

波能转换装置的能量最大化控制准则可表示为[6]

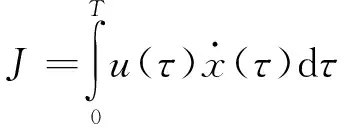
(1)

根据装置运动方程及约束条件，求取最大PTO力，控制发电机转速，跟踪最大PTO力曲线，实现最大波能捕获。

单一垂直自由度运动浮子的运动方程为[7]

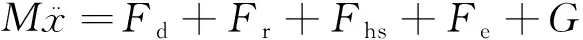
(2)

式中:Fd为入射波作用在浮子上的力；Fr为辐射力；Fhs为静浮力，假设浮子位移x=0时，Fhs=0，则Fhs=-Kx，其中K为静水恢复力刚度系数；Fe为电机反电磁力；G为浮子自身重力。

当入射波为规则波时，辐射力可表示为

(3)

式中：A为附加质量；B为附加阻尼。

反电磁力可以表示为速度与位移的线性组合：

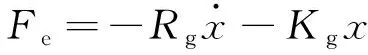
(4)

式中:Rg为阻尼系数;Kg为刚度系数。

浮子重力G为常数，只会影响系统的平衡位置。浮子运动方程可简化为

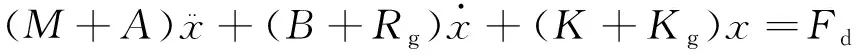
(5)

图2 浮子运动等效电路模型

等效电阻R2上捕获的功率即为发电机捕获功率，其表达式为

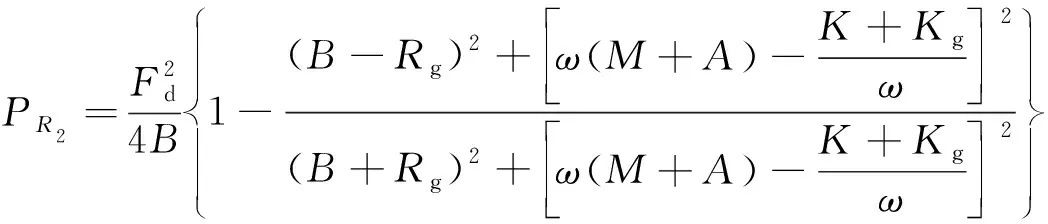
(6)

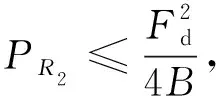
以振荡水柱式波浪发电系统为研究对象，构建气室中涡轮机的数学模型[8]：

(7)

式中:dP为涡轮两端的压降;Ca为功率系数;Ct为扭矩系数;k为涡轮常数；a为涡轮面积；r为涡轮半径，vx为气流速度；ω为涡轮角速度；b为叶片跨度；n为叶片数量；l为叶片弦长；φ为流量系数；q为流量速率；η为涡轮的效率；P为涡轮机功率。

由此可见，通过功率系数和扭矩系数可计算出涡轮机功率和扭矩。根据涡轮机的动力学特性，当气流速度超过临界值时，涡轮机性能急剧下降，称为停滞现象。φ控制Ct，存在一个特定φ*，当φ>φ*时，Ct先减小到零然后逐渐增加；当φ<φ*时，Ct持续衰减到零，该点称为停滞点。考虑到流量系数φ总是从零振荡到一个稳定值，则φ=0～φ*。通过控制涡轮机转速，跟踪气流速度，保持流量系数稳定在停滞点附近，取得最大扭矩系数及最大波能捕获。

波浪变化，导致波能转换装置输出电能、电压变化，电能质量不佳无法满足并网要求，可以通过功率变换器进行处理。直流侧的储能系统可有效改善功率波动，提高电能质量，也可通过控制电机转速实现变速恒频运行。

2 滑模变结构控制在波能转换系统应用

波能转换系统激励难以预测，波浪运动在不同地域、不同时间表现出强烈复杂性，鲁棒性强的简单结构控制器尤为必要。

滑模控制基本应用框图如图3所示。

图3 滑模控制基本应用框图

其中，r(t)为参考量，e(t)为误差量，u(t)为控制量，y(t)为输出量。本质上，滑模变结构控制是一种不连续的开关型控制，根据系统当前状态不断变化，迫使系统沿预定“滑动模态”状态轨迹进行运动。该控制器结构简单、响应快速、对参数变化及扰动不敏感，滑动模态可自行设计，且与系统参数和扰动无关。

振荡水柱式可变涡轮转速双馈波浪发电系统(DFIG)，电机定子绕组直接接入电网，转子绕组通过变频器接入电网。根据涡轮机动力学特性，当气流速度超过某阈值，涡轮机性能将急剧下降，称为停滞现象。为了避免此现象并同时捕获最大波浪能，需根据涡轮机特性曲线合理选取流量系数，跟踪理想转速。转子电流采用滑模变结构跟踪控制策略[9-10]，控制转速，系统鲁棒性好，可有效抑制外部扰动，并入电网电流波形稳定。但控制参数选择对控制器性能影响较大，大增益控制会产生严重抖振现象，导致系统轴承机构产生应力，系统不稳定；小增益控制可能不满足稳定性条件。因此，控制器增益选择采用智能优化算法[11]，可有效减少滑动模块抖动，防止系统失稳。

直驱式永磁直线波浪发电系统，当浮子运动频率等于波浪频率时，系统发生共振现象，得到自然频率ω0，波能捕获最大。为了使浮子运动频率跟踪波浪频率，采用等效滑模方法控制电机反电磁力Fe，跟踪q轴理想电流。在滑模控制切换项中植入自适应控制律[12]，可显著降低海浪波动及参数扰动对系统的影响，系统鲁棒性好。通过设计合适的滑动变量，能够有效消除系统建模误差和波浪预测误差，实现不规则波浪控制下的最优跟踪控制[13]。

点吸收式液压传动波浪发电系统输出电能稳定性好，通过调节斜盘倾斜角控制液压马达排量，实现电机转速控制。为了克服波浪变化引起的转速波动，依据Lyapunov方程设计自适应控制参数，由积分滑模控制补偿自适应律误差[14]，实现扰动状态下的稳定功率输出。

电机运行过程中存在混沌现象。随机波浪可能导致系统在某一特定状态下发生谐振，定子电流、转矩振荡产生的不规则振动及噪声会使系统进入混沌状态，影响运行稳定性。采用BP神经网络调节滑模变结构控制器参数，结合粒子群算法(PSO)确定最优控制参数，使系统脱离混沌状态同时实现最优控制策略[15]。因为PSO中适应度函数包括了系统状态变量响应时间和超调，所以经过控制器输出的电流信号响应时间快、超调小，鲁棒性好。

滑模变结构控制凭借着响应快速、鲁棒性强的特点，能够有效控制处在不确定干扰下的波浪发电系统。然而，开关函数存在的死区现象会产生一个抖振区间，影响电机性能。目前的波浪发电系统控制中，滑模变结构控制虽有应用但并不多，研究资料相对较少。将滑模控制与人工智能算法、自适应控制等其他控制方法相结合，消除滑模抖振，提高鲁棒性应是未来可行的研究方向之一。

3 自适应控制在波能转换系统的应用

应用自适应PI控制器，可控制波浪发电机组在变化波浪工况工作在最优运行点[16]。传统PI控制离线计算增益，可能导致变化海况时工作点偏移。采用无迹卡尔曼滤波估计波浪主频，计算控制器增益及控制律。试验表明，在复杂波况下该控制方法能快速响应和调整控制器参数，有较强的非线性时变系统控制能力。自适应控制基本应用框图如图4所示。

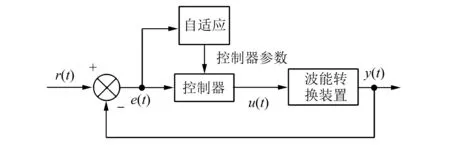
图4 自适应控制基本应用框图

真实海浪通常出现在一个频率频谱中，主导频率随时变化，波周期非共振工况下，传统线性点吸收式波能转换装置运行性能较差。与线性控制器相比，双稳态功率捕获机制控制性能更优[17]，但对低振幅激励下的波浪，可能无法越过补平衡点势垒，陷入局部势井中，吸收效率下降。若在双稳态系统中加入2个辅助弹簧，可实现自适应不平衡点势垒，在低振幅激励情况下依旧可以实现势井间振荡。通过选取适当的辅助弹簧弹性系数，能够获得较大的功率捕获宽度比。由于引入了负刚度，自适应双稳态波能转换装置峰值频率，低于线性波能转换装置。

良好的机械及控制器设计，可显著提高波能转换效率。不同海况下波能转换装置的动力学模型变化较大，采用自适应策略识别系统辐射力、激励力参数，以参数估计误差在线调整自适应律，实现指数误差收敛。将调整后的动力学模型应用非因果最优控制(LOC)策略，控制装置在最大波能捕获工作点上。所提自适应控制器能快速计算系统参数，保证系统控制性能，同时通过Lyapunov函数验证系统收敛性，为解决传统模型时变参数提供了一种有效的解决方法[18]。

基于线性模型的波能转换装置在最大波能捕获方面具有计算简单的优势，但这一类模型通常是将静止水面作为平衡点，假设运动幅度小进行计算分析，对于大幅度变化波浪来说捕获效率较低。采用自适应滚动优化伪谱控制器[19]，将波浪激励力伪谱化，以半程切比雪夫傅里叶函数为基函数，构建动力学模型，通过设计遗忘因子λ迭代计算系统运动方程参数。在最大化吸收能量J的同时，计算当前伪谱函数下的系统残差并使其归零，获得最佳运动轨迹；最后通过反步法实时跟踪最佳运动轨迹。对波能转换装置具有普适性，提高变化波况下控制器性能。与恒定控制模型相比，所产生最优运动轨迹振幅位移小，捕获能量更多。

最大功率点跟踪(MPPT)技术在太阳能、风能运用已较为成熟，但在波浪能方面文献较少。为了避免系统非线性模型建模的不确定性，导致自然频率不匹配，采用扰动观察法跟踪波浪发电系统最大功率点。 通过控制与发电机机端直接相连的DC-DC升压斩波电路占空比，调节负载两端电压，控制电机电磁力。采用自适应算法[20]，通过计算连续时间间隔内的输出功率之差来调整步长，加快跟踪过程，避免振荡。与传统固定步长扰动观察法相比，自适应步长提高了响应速度，输出电功率和纹波均有较好的性能。

自适应控制系统能够实时调整控制器参数，以适应波浪激励的变化，有效跟踪期望值。但由于参数估计方法均是在无穷处收敛，其时效性还有待考证。并且对于波浪发电系统而言，难以做到高精度的测量，这又会对系统性能产生影响。换而言之，将自适应控制与其他先进控制算法结合，提高收敛速度，同时采用无传感器对参数进行测量，将是未来的研究方向之一。

4 最优控制在波能转换系统的应用

MPPT已在风力发电和光伏发电等方面取得众多成果，将MPPT控制策略应用于波能转换装置，采用观察扰动法将当前吸收的平均功率与前一时刻的平均功率进行比较，若功率增加则MPPT控制保持不变；若功率减小则MPPT控制动作改变符号，通过设置合适步长使系统运行在最佳工作点[21]。算法无需预测波浪，对非线性系统数学模型精确度要求较低。通过循环MPPT控制算法，采用正弦波信号对负载标称值进行调制。在每个MPPT周期末端，通过归一化调制信号和输出功率P的协方差，确定下一时刻负载变化量。仿真结果表明，循环算法控制更好，能将标称负载调节到最佳值[22]。将波能转换装置与电力电子器件相连，通过控制DC-DC变换器中Boost电路IGBT导通时间控制负载电压，实现最优阻抗匹配。

最优控制的基本应用框图如图5所示。为了研究不规则波浪最优控制问题，文献[23]将基于矩的鲁棒优化控制应用到波能转换装置上。将系统原始最优控制问题映射转化为凹二次规划(QP)问题[24]，替换消除了系统状态变量，系统优化问题简化为系统控制变量优化问题，可采用先进算法求解。矩域框架可处理设备和PTO系统的物理约束，确保最佳控制输入可行，保证系统耐用性，在能量捕获与计算时间上优于模型预测控制(MPC)策略。考虑线性化模型参数的不确定性，扩展矩域框架，根据最差性能(WCP)策略更新控制率，将最优控制问题转化为最小极大值QP问题，提高系统鲁棒性[25]。实际系统参数偏差无法精确测定，如何设置参数最大偏差，仍有待研究。

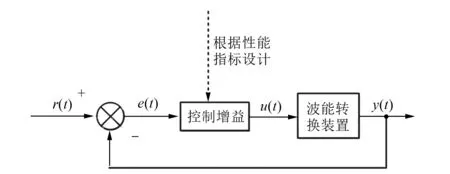
图5 最优控制基本应用框图

限于波能转换系统模型精度，基于模型的控制策略有效性欠佳，未建模的动态过程不仅会使装置控制性能下降，采用高复杂度模型描述不确定性系统会增加系统计算负担。将波能系统控制问题转换为有约束的最优控制问题，采用自适应动态规划策略进行求解，可满足性能要求[26]。系统控制目标函数被重新设计为求解哈密顿方程极值点问题，运用神经网络逼近成本函数，神经元采用含时间变量的激活函数，权重自适应调整。通过动态调整成本函数中的R参数，可有效限制电机转矩和浮子升沉运动范围，鲁棒性好。

一般会将波能转换装置简化为单一自由度系统，通过构建完全匹配的控制器捕获波能，但这种理想模型无法代表实际系统。文献[27]针对多自由度的波能转换装置WaveSub，提出一种主动控制策略，通过线性二次型调节器状态反馈控制器优化多自由度PTO系统控制率增益，实现最优速度控制。采用扩展卡尔曼滤波算法估计每个自由度的振幅和频率，同时约束速度，得到速度参考增益时变矩阵。与最佳谐振控制的无源系统相比，虽然瞬时功率平滑度下降，但平均功率增加了80%。

最优控制设计的性能指标考虑了波能转换装置的物理限制，波浪发电系统能够更加合理的实现最大功率输出。如何设计波浪发电系统性能指标会成为影响系统输出功率和稳定性的关键因素。

5 智能算法在波能转换系统的应用

智能算法一般用来解决优化问题，基本原理是搜索领域函数，找出替代原值的更优值；通过大量历史数据训练模型，控制目标函数逼近任意非线性函数，无须对象精确数学模型。智能算法基本应用框图如图6所示。

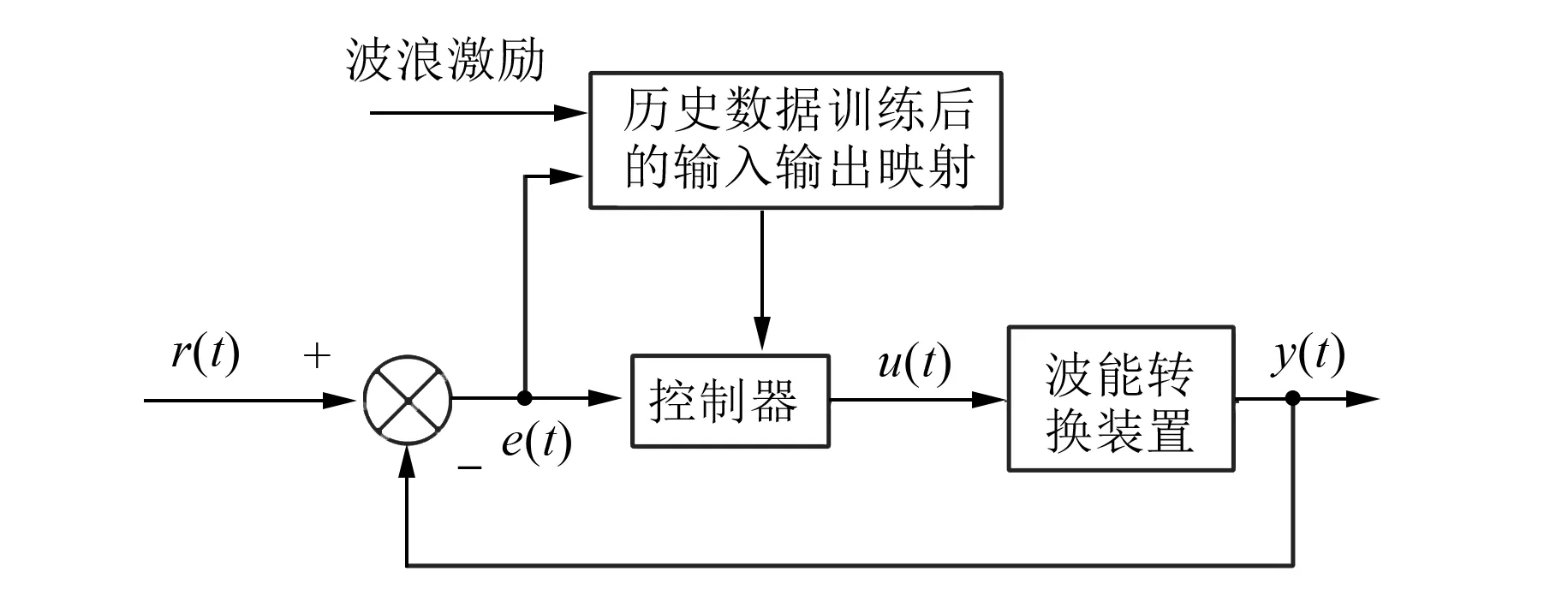
图6 智能算法基本应用框图

直驱式波浪发电装置捕获的波浪能与电机反电磁力Fe密切相关。根据共振原理，当Fe中的有功、无功阻尼系数为某一波浪频率下的特定值时，系统达到共振状态，捕获最大功率。针对传统粒子群及遗传算法存在早熟、局部收敛缺陷，文献[28]采用模拟退火粒子群算法筛选系统阻尼，利用其有一定概率暂时接受新状态的特性，避免搜索陷入局部极值。仿真表明，模拟退火粒子群算法收敛快速、全局最优。当波浪频率发生改变时，需改变系统阻尼，使波能转换装置工作在最优负载状态，捕获最大波能。为此，文献[29]采用加入混沌算子的混沌捕焰新算法，有效提高了全局搜索能力，避免陷入局部最优。仿真表明，当波浪频率发生改变，采用新算法系统依旧可以使激励力与浮子速度保持同相，捕获最大波能。

经典控制器为了跟踪最优控制律，需要了解未来波浪激励力的信息。波浪激励力的预测费用昂贵，同时预测的精确度也无法保证，当系统偏离最优控制一定范围时，捕获的功率急剧下降。为此，文献[30]使用一种新的反向传播神经网络构建出系统输入-输出的映射关系，并采用经卡尔曼滤波后的激励历史数据对模型进行训练所得到的最优反电磁力与模型预测控制、无功控制相比，捕获波能效率显著提升。

人工神经网络具有趋近任意非线性函数的能力，通过训练神经网络，并将历史训练集储存在神经元内部，以权重求和形式逼近目标函数。利用波浪在当前取样周期内的周期、幅值、阻尼系数、刚度系数与捕获功率、最大位移的映射关系，根据成本函数选出下一周期的最优阻尼、刚度系数[31]。该方法能够迅速处理设备响应的变化，对于变化的海况有良好的控制效果。针对阿基米德波浪摆，结合神经网络算法与内模控制[32]，分别以Elman及局部递归神经网络为控制器和过程模型，采用Levenberg-Marquardt算法训练神经网络，使波浪激励力与浮子速度同相位，捕获最大波浪能，能量吸收提升了160%，并可实现不同季节切换控制，改善捕获结果，仿真验证了模型鲁棒性。基于递归小波算法的Elman神经网络控制器[33]，可快速响应负荷变化引起的暂态过程；以转速误差与母线电压波动为训练集，小波函数为激活函数，扩大搜索范围，通过改进的引力搜索算法调节学习速率，减少训练时间，实现q轴电流控制。试验证明，在不同负荷干扰与故障下，控制性能优于PI控制与递归模糊神经网络(RFNN)，可更快实现转速及母线电压稳定，鲁棒性强，可靠性高。

智能优化算法通过训练历史数据，得到输入与输出的映射关系，有效地解决波浪发电系统的建模误差问题，实现了控制器参数的动态优化调整。然而由于理论研究的不足，难以保证解的最优性。

6 模糊控制在波能转换系统的应用

模糊控制以模糊集理论、模糊语言变量和模糊逻辑推理为基础，可从行为上模仿人的模糊推理和决策过程，将专家经验用于控制系统，模糊控制器基本应用框图如图7所示。

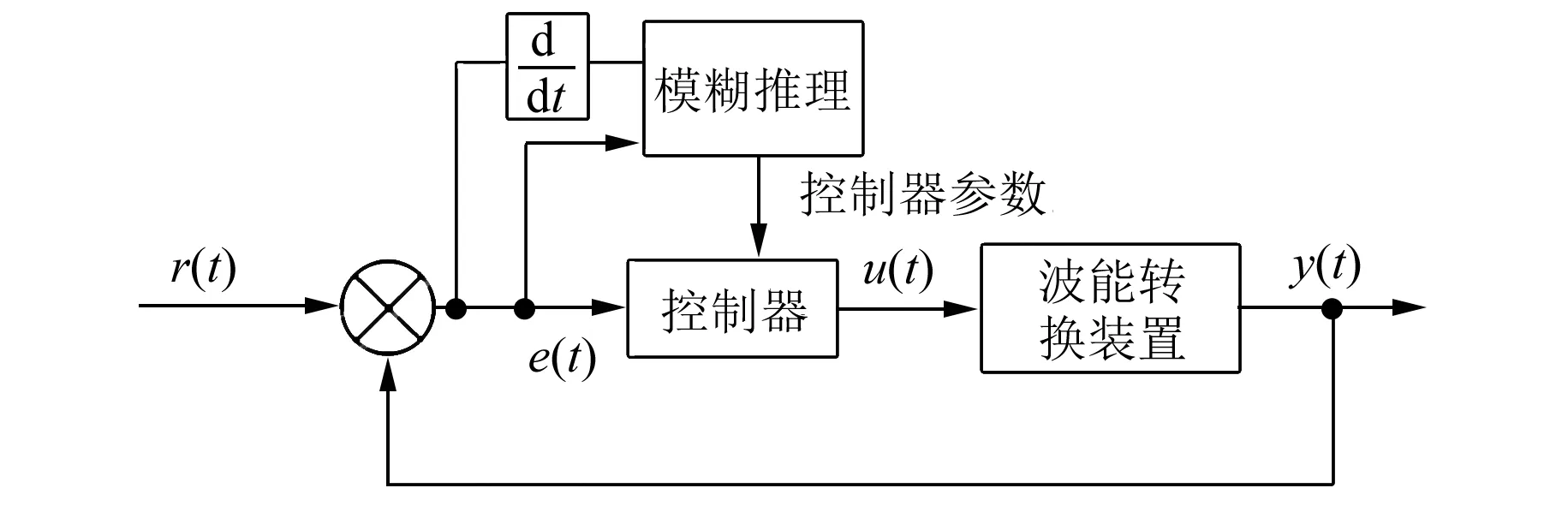
图7 模糊控制器基本应用框图

波浪能量的产生主要由地理位置和自然环境决定，是一种不确定、随机能量。由于波浪波动性较大，波浪发电输出电能使系统稳定性降低。为了提高波浪发电系统稳定性，改善电能质量，引入模糊神经元PID控制器。以系统转速误差及变化率为模糊控制策略输入，实现单神经元放大增益K自整定。采用系统误差大时K大，误差小时K小的模糊规则表，获得更快响应速度和更高稳定性能[34]。仿真表明，不规则波输入情况下，模糊神经元PID控制策略依旧能通过控制发电机转子电压变化，控制发电机转速恒定，自适应性和抗干扰能较好力。由于海水腐蚀，传统波能转换装置机械传感器可能会导致测量数据误差，采用无速度传感器控制策略[35]，通过扩张卡尔曼滤波器(EKF)在线估计系统状态，设置模糊PI控制器实现实时控制，此时的速度观测器误差仅为0.004 5 m/s，控制器鲁棒性好、精度高，能有效降低传统速度传感器维护费用。

为了实现不规则波下的最大功率捕获，采用模糊MPPT控制策略[36]，控制器输入为平均功率变化量，输出的占空比信号作用在Buck-Boost电路的电力电子器件上，获得当前波况下的最优负载。实际海况下，通过蓄电池稳定输出功率，可改善电能质量。

对于采用共振原理捕获最大波能的系统，其自然频率与波浪频率间有偏差，受波浪周期变化影响，点吸收式波能转换装置输出功率会显著降低。运用重心法Mamdani型模糊推理系统进行去模糊处理[37]，控制波浪发电系统阻尼及刚度系数，复杂波浪情况下，系统可增加14%能量捕获。为了鲁棒性更好，采用PSO选取模糊隶属函数参数[38]。通过对Gauss MF函数中标准差和均值进行寻优，动态调整隶属函数。与模糊逻辑控制器(FLC)相比，PSO-FLC有相似平均峰值比，但平均功率捕获多15%，且即使存在扰动，仍能运行在最优点附近，系统鲁棒性增强。波能转换装置存在非线性，系统动态模型识别会产生误差，导致系统整体性能下降。为了提高系统鲁棒性，设计优化控制算法，通过控制线性时不变系统参数的奇异值，优化系统参数的最小谱范数，使其远离不稳定运行状态。采用遗传算法(GA)寻找成本函数最小值，基于最小二次型(LQ)控制器设计鲁棒控制方案。结合该控制器与模糊控制器[39]，针对系统模型参数改变6%情况下，该控制器产生的能源损失为17%，远低于不加控制时的77%。但此时的GA是离线优化参数，实时性欠佳。

实际工况中，瞬时控制阻尼系数不切实际，需要高功率实现瞬时设置和精确控制,技术困难，经济性差。通过在浮标下设置8个两两对称的弹簧，通过液压缸激活，以量化方式控制阻尼系数[40]，但复杂波浪下的量化控制可能会使系统自然频率产生偏差，无法达到共振状态，为此需在浮标内加入水箱，通过FLC策略控制泵控制浮标质量，从而改变系统自然频率。仿真表明，量化策略和FLC可避免高成本和高技术需求，同时能够有效补偿由于量化效应带来的频率失配问题。

针对非线性的波浪发电系统，模糊控制因具有设计语言简单、鲁棒性强的特点得到广泛应用。但是，简单的信息处理将导致系统的动态性能变差，这不利于跟踪时刻变化的波浪激励。因此，模糊规则的制定和模糊隶属度的选取在很大程度上决定了系统的动态性能。

7 无源性控制在波能转换系统的应用

无源性控制出发点是能量控制，根据系统控制需求，按照希望方式安排能量函数分布，进而实现控制目的。无源控制器基本应用框图如图8所示。波浪发电控制本质上是一种能量传递和分布问题，应用无源性控制，能够很好地处理系统动态性能问题。

图8 无源控制器基本应用框图

应用互联-阻尼配置的无源控制器，将浮子动力学模型转换为端口受控的耗散哈密顿模型形式，得到系统互联矩阵J和阻尼矩阵R。对系统状态误差设计注入阻尼矩阵和系统能量分配矩阵，实现误差在期望点处快速收敛。根据系统能量函数He时间导数在期望处为零，构建系统控制律；采用矢量控制方案，跟踪控制dq轴电流，实现波能最大捕获[41-42],并保持复杂波况下波浪发电机组运行平稳。直驱式波浪发电系统的浮子运动到最高或最低点附近时存在过零低速区，此时发电机效率降低。根据电机效率曲线，采用无源性控制获得电磁力期望值，通过控制q轴电流实现：动子高速负载运行发电，低速空载运行进行机械储能[43]。切换过程采用微分平滑策略，保证了电机瞬时功率的平滑过渡。仿真结果证明了分段控制策略的有效性。

波能转换装置的无源性控制目前研究较少，从能量角度出发，能够对控制行为进行合理的物理解释，是连通控制理论学者和工程师的桥梁。实际运用过程中无源控制器控制效果往往受限于波能装置建模的精确度。在保证系统无源的情况下，增加控制器鲁棒性，能够极大地提高系统的稳定性。

8 结 语

各种先进控制技术方案，已或多或少地应用到波能转换装置中，但总的来看，还处于初级研究阶段。波浪的随机性、不确定性，波能转换装置参数的非线性，系统动态过程建模的准确性，均将严重干扰运行，导致系统无法稳定运行在工作点上。实际上，每种控制方法均有其优缺点，如何充分发挥优点避开不足，是控制研究的永恒课题。采用2种及2种以上的互补优化混合控制算法，提高控制的精度和速度、优化控制成本，是未来研究的主要方向。而波浪预测、多自由度运动状态分析、系统数学模型构建也是未来解决控制问题分析的基础。

波能转换系统的关键问题在于提高波能转换效率和改善电能质量。采用电路共振原理和最佳控制的策略能提高转换效率；采用自适应鲁棒控制的机组能够有效提高电能质量。由于波浪能的分散性和随机性，目前的波能转换装置多为小型机组且不接入电网，先进控制技术可提高捕获效率及并网电能质量稳定性，也是未来发展方向。