BLDCM霍尔传感器故障诊断与容错控制*

王 凯，刘细平，张 云，陈 苗

(江西理工大学 电气工程与自动化学院，江西 赣州 341000)

0 引 言

无刷直流电机(BLDCM)具有效率高、体积小、机械结构简单等优点,已逐渐成为电机调速领域的热门研究对象。通常，电机转子位置和转速多采用光电编码器、旋转变压器、磁编码器等进行采集，但因体积较大，硬件成本高及接口线路复杂等因素制约了其在低成本驱动领域的发展。BLDCM中使用成本较低及体积较小的霍尔传感器作为位置检测元件在一定程度可解决此问题，但其在恶劣情况下易受到损坏。因此，为了提高BLDCM驱动系统的安全及可靠性，开展霍尔传感器故障诊断及其容错控制的研究具有十分重要的意义。

许多专家学者针对霍尔传感器故障诊断和容错控制的方法进行了深入的研究。文献[1]通过比较相邻2个霍尔换相区的时间段来实现霍尔传感器的故障诊断，但其在诊断时需等到后一轮霍尔换相产生才能进行，故障诊断效率较低。而在容错控制时，则利用正常霍尔传感器换相时间间隔替换故障时间间隔，其主要取决于上一轮换相时间，导致容错控制出现滞后。文献[2]提出基于线电压频谱分析进行诊断的方法，但复杂的离散傅里叶变换计算，影响故障诊断效率和容错控制效果。文献[3]通过对比反电动势观测器与霍尔传感器估算的转子位置来判断当前霍尔传感器故障情况，并进行容错控制，但系统复杂和成本较高，且霍尔传感器位置估算易受机械安装偏差的影响，导致对比差值过大而使故障诊断失效。文献[4]在电机加减负载情况下,通过加入时间补偿系数，比较2个相邻霍尔换相区的时间宽度，从而判断当前霍尔传感器的状态，但时间补偿系数依赖前期调参，系数无法随系统变化，因此易导致故障诊断失效。文献[5]提出了3种容错控制方法，其中基于外插法和闭环角度观测器的容错控制均会使估算角度出现明显滞后，而利用霍尔矢量跟踪观测器时矢量变换将会增大控制器运算时间。文献[6]通过试验对比3种改进的霍尔传感器故障补偿策略，其中基于降阶观测器补偿方法测试效果最佳，能有效地削弱因霍尔位置传感器机械偏差造成电机容错时转速波动的影响。文献[7]提出基于霍尔状态序列的故障检测和容错控制方法，其故障诊断效率较低，容错控制中位置估算存在较大波动。

基于上述研究，为了提高故障诊断速率和降低因机械安装导致霍尔传感器磁极检测偏差对位置估算的影响[8]，需深入研究BLDCM霍尔传感器故障诊断方法及容错控制技术。本文通过比较最小二乘法拟合曲线与一阶泰勒算法两者估算的位置值，实时诊断霍尔传感器工作状况，有效提升诊断效率。在霍尔传感器出现故障时，利用正常霍尔传感器跳变沿的时间间隔对故障下的跳变沿时间实施重构，并重新建立坐标点及拟合曲线，利用重构后的拟合曲线对系统采取容错控制。理论分析和试验结果表明,该方法能够较好地实现BLDCM霍尔传感器的故障诊断及容错控制，有效改善故障下的系统性能。

1 BLDCM驱动系统

1.1 基于霍尔传感器BLDCM驱动系统

图1所示为BLDCM驱动系统基本结构。主要由控制器、驱动器、BLDCM及霍尔传感器等组成。BLDCM转子位置信息的采集是其实现矢量控制的关键[9]，为整个驱动系统稳定的前提条件。通过霍尔传感器只能在每个电周期内采集6个离散的位置信号，将无法实现矢量控制。因此，需研究相应算法估算矢量控制所需的转子位置信息，并将估算结果进行微分处理以获取平均速度和二次微分后的平均加速度。然而转子速度及位置估算的精度将决定BLDCM矢量控制性能的优劣，进一步影响系统的稳定性。

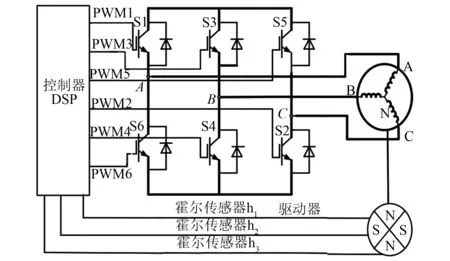
图1 BLDCM驱动系统的基本结构

1.2 基于一阶泰勒的位置估算法

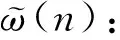
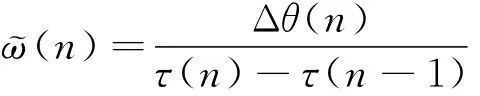
(1)

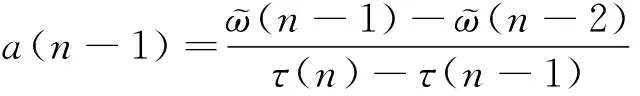
(2)

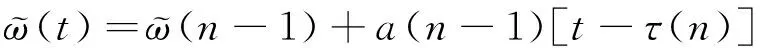
(3)

根据式(3)估算当前位置的转子速度，设转子初始位置为θe(n),则可估算当前转子位置θm(t)：

a(n-1)[t-τ(n)]2

(4)

2 霍尔传感器故障诊断

当前霍尔传感器故障诊断的方法主要有：(1)基于霍尔状态序列的故障诊断方法。其利用1个电周期内霍尔传感器固定6个状态顺序变化以实现故障诊断[11]。(2)利用霍尔跳变沿序列的故障诊断方法。霍尔的每个跳变沿均对应相应的转子位置，通过判断6个跳变沿顺序，能够判断是否存在故障。(3)相邻霍尔扇区时间间隔比较法。通过对比相邻扇区时间是否超出了误差范围，从而判定霍尔传感器当前状态。

上述霍尔传感器故障诊断方法易受因机械安装导致霍尔传感器磁极检测偏差对位置估算的影响，且需在下一轮霍尔跳变沿产生才能进行故障诊断。为了解决此问题，通过引入最小二乘法对转子位置进行拟合，能够较大程度削弱机械安装对霍尔传感器磁极检测造成的偏差。通过利用1个电周期内6个跳变沿对应的时间间隔及边界位置进行插值，可拟合成一个电机转子位置估算多项式。转子位置插值曲线如图2所示。利用最小二乘法拟合曲线作为与一阶泰勒算法的评价模型，对比两者位置估算的差值，可实现霍尔传感器实时故障诊断。

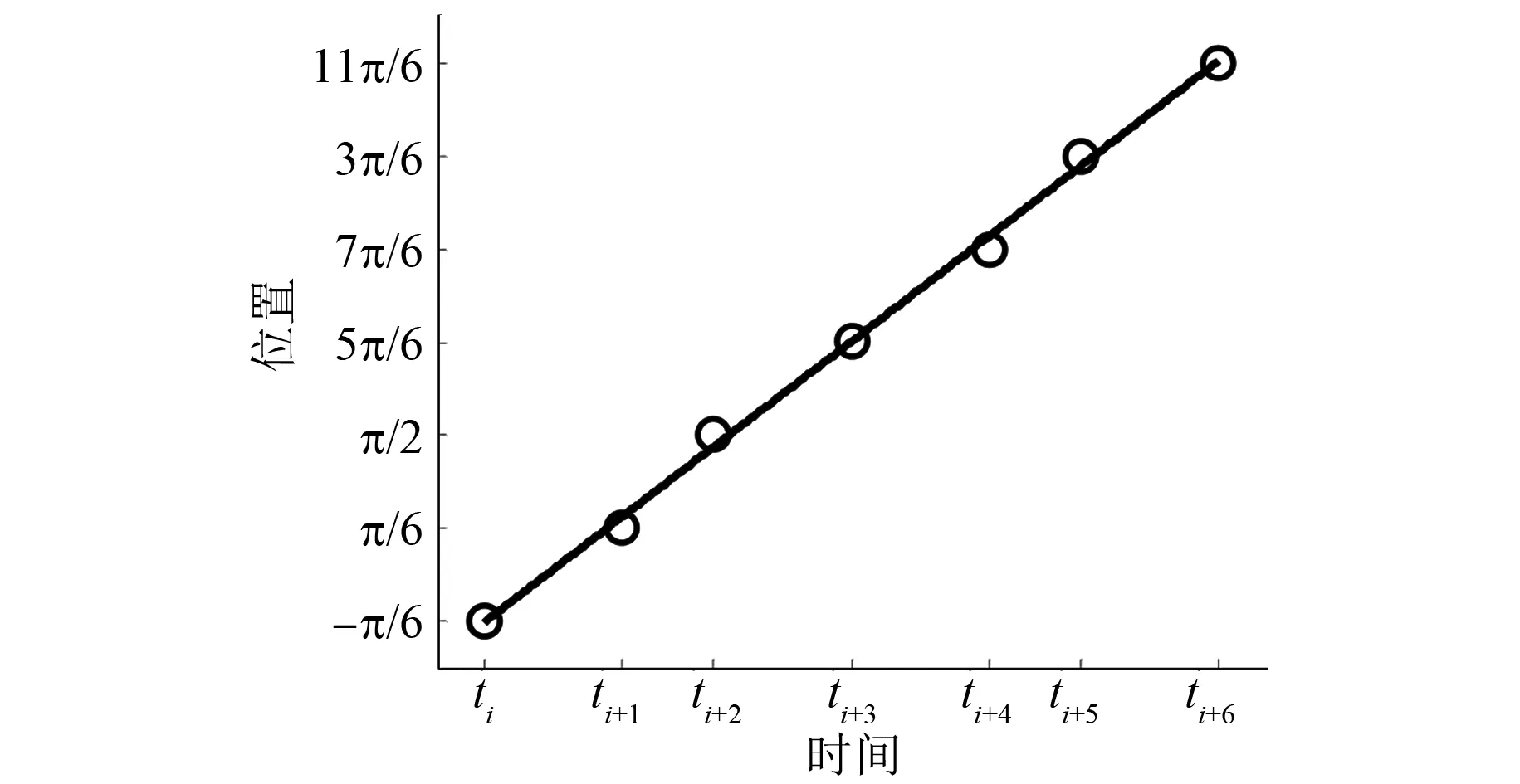
图2 转子位置插值曲线

将一阶泰勒展开式为二次多项式，为了满足同等条件，需利用最小二乘法拟合成二次多项式。根据最小二乘法二次多项式可得：

S(x)=b0x2+b1x+b2

(5)

式中：Qmin为两者残差最小平方和;S(xi)为二次多项式估算值；yi为一阶泰勒估算。

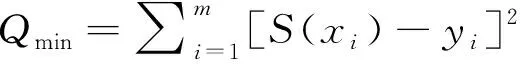
(6)

式(6)为一个求极值的问题，多元函数求极值是最小二乘法多项式必要条件，对Qmin求偏导数后，极值表示为

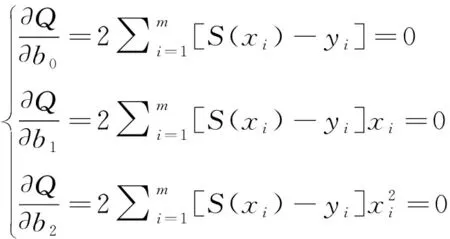
(7)

式(7)为关于b0、b1、b2的线性方程组，称为法方程[12]，用矩阵表示为

(8)

由式(8)可证明，系数矩阵为一个非奇异矩阵，必然存在唯一的解(b0、b1、b2)。通过求多元函数极值，可推导出b0、b1、b2系数为

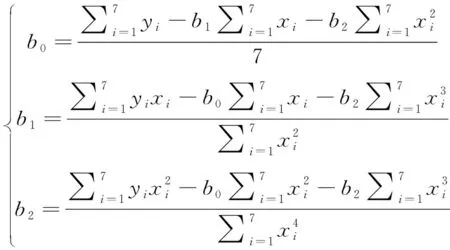
(9)

求解b0、b1、b23个系数需获取相应霍尔传感器跳变沿对应的时间间隔及边界位置，横坐标xi为霍尔跳变沿的时间间隔，记为Ti～Ti+5，yi为边界位置[13]。插值点的坐标如表1所示。

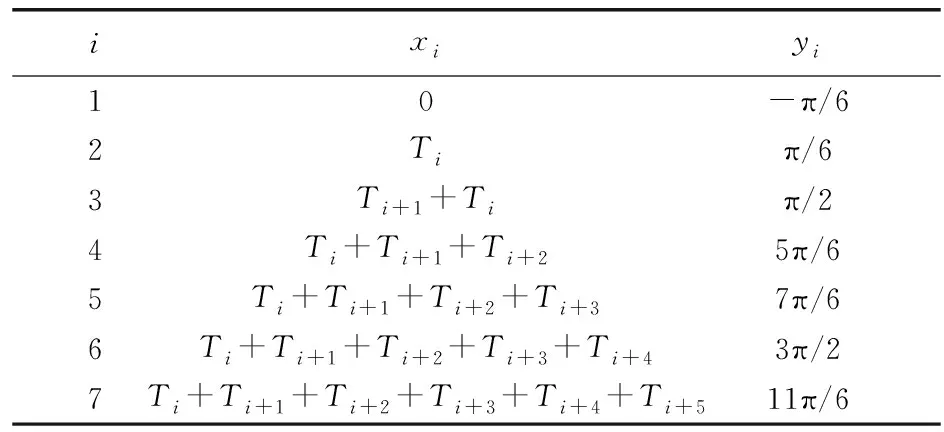
表1 插值点的坐标

每产生6个霍尔跳变沿，需对二次多项式重新拟合。设θe(t)是初始霍尔边界位置，θg(t)为当前估算的位置。可推导出最小二乘法转子位置估算方程：

θg(t)=θe(t)+b0t2+b1t2+b2

(10)

当程序触发中断时，通过寄存器获取当前时间，依次代入一阶泰勒公式式(4)与最小二乘法二次多项式(10)中，可得当前时刻估算的一阶泰勒位置值θm(t)与最小二乘法位置值θg(t)。通过预先设定差值εerr，比较2个位置θm(t)和θg(t)，判断当前霍尔传感器是否在位置估算范围内，若差值超出εerr[14]，可判定当前跳变沿的霍尔传感器出现故障。有：

|θg(n)-θm(n)|>εerr

(11)

上述分析表明，利用最小二乘法多项式作为一阶泰勒位置估算的评价模型，可削弱机械安装给霍尔传感器故障检测造成的影响，且不存在完成下一轮霍尔跳变沿才能进入故障诊断的问题，可有效提高诊断效率及准确性。

3 基于最小二乘法的容错控制

当霍尔传感器出现故障时，其输出信号将失效，并导致控制器无法获取原有相邻跳变沿时间。此时需捕获正常霍尔传感器的跳变沿时间，以便估算故障时的电机平均速度及加速度，并由此推导跳变沿丢失处及其前一个跳变沿的时间间隔，重新对最小二乘法二次多项式重构，从而实现容错控制。下面分析单霍尔和双霍尔故障情况。

单霍尔故障情况如图3所示，若h3出现故障，跳变沿将会丢失P2和P5，一个电周期内，有效霍尔跳变沿由原来的6个变成4个，Δθ(n-1)和Δθ(n+1)对应位置间隔由正常的Δθ=π/3变成Δθ=2π/3。其他2类单霍尔传感器h1、h2故障下的跳变沿丢失及位置间隔增大的情况与h3故障类似。

双霍尔故障情况如图4所示，若h2与h3发生故障，跳变沿将会丢失P2、P3、P5和P6，一个电周期内，有效跳变沿由原来的6个变成2个，Δθ(n-1)和Δθ(n+1)对应位置间隔由正常的Δθ=π/3变为Δθ=π。其他两类双霍尔传感器故障分别为h1和h2、h1和h3故障下跳变沿的丢失及位置间隔增大情况，与h2、h3故障类似。

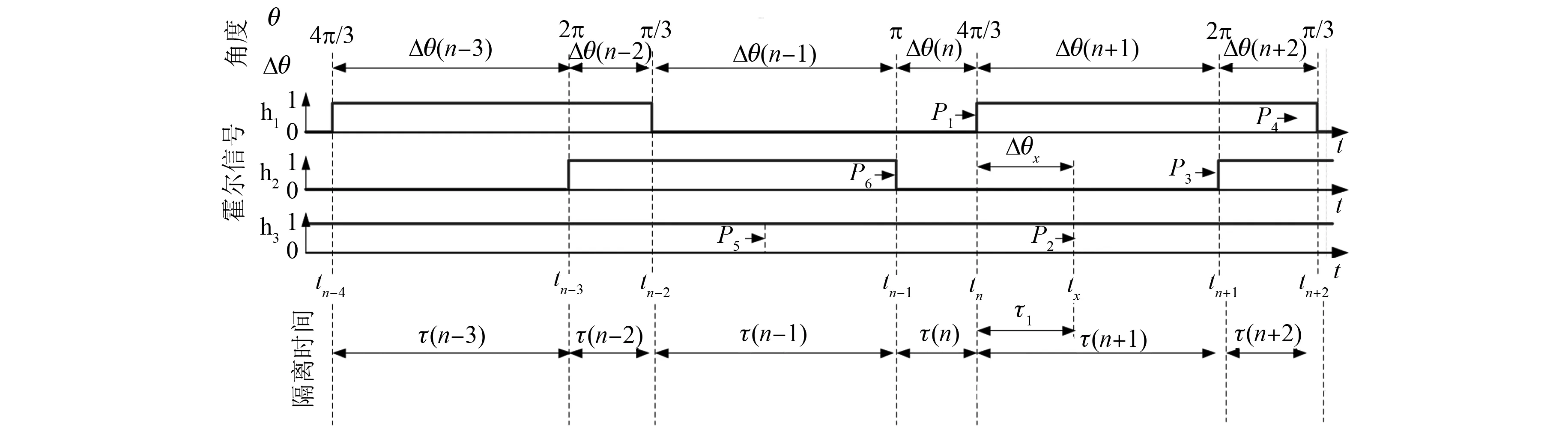
图3 单霍尔故障情况

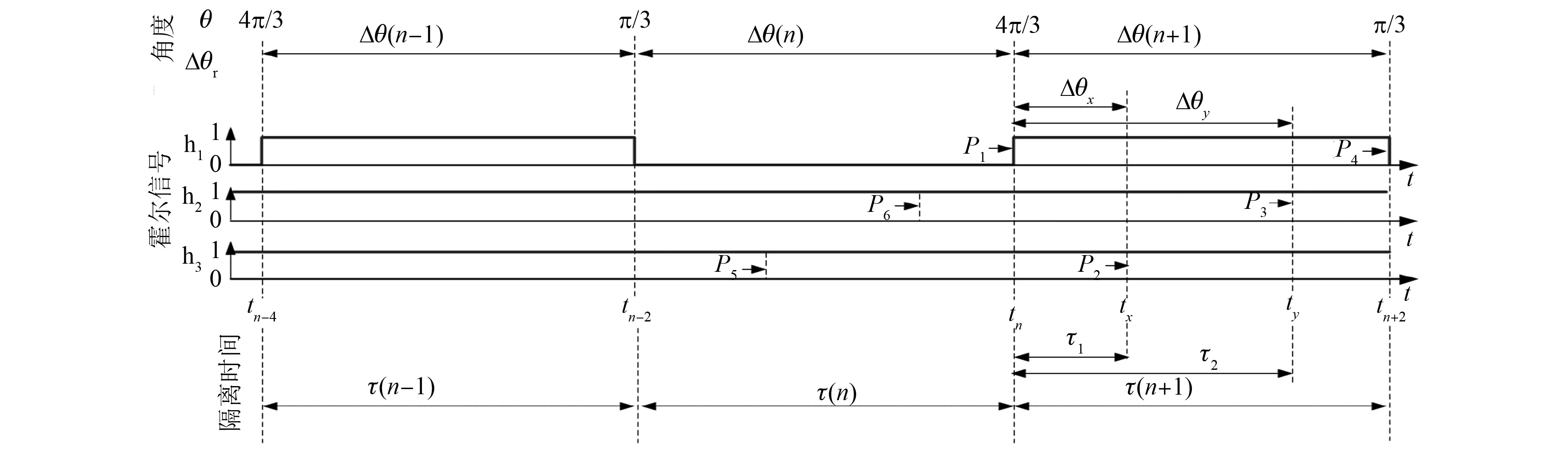
图4 双霍尔故障情况

若霍尔传感器出现故障，需在丢失跳变沿的前一个跳变沿tn处估算出与tx处丢失跳变沿之间的时间间隔，记为τx。Δθx为丢失跳变沿处与其前面相邻的跳变沿处之间的位置间隔。由式(3)和式(4)可得：

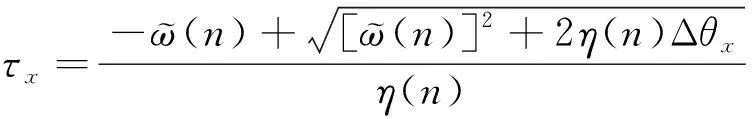
(12)

当电机加速度较小时，式(12)将导致估算的时间间隔出现较大偏差。当匀速运动时，加速度为零，时间间隔将会无穷大，这将导致程序中的寄存器溢出，需对式(12)进行转化：

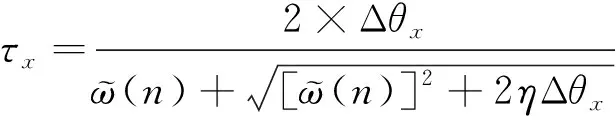
(13)

当h3发生故障时，将不会产生跳变沿信号P2，P2跳变沿处与其前面相邻的跳变沿处之间的位置间隔记为Δθx=π/3，重构后的时间间隔记为τ1。将Δθx=π/3代入式(13)，可得：

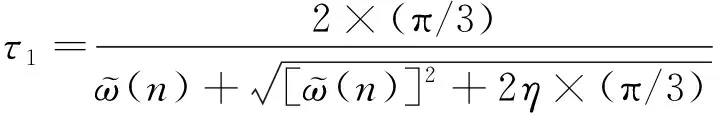
(14)

通过式(14)可估算出时间间隔τ1，重新获得单霍尔故障下的插值表，如表2所示。

表2 单霍尔故障插值坐标表

类似地，在双霍尔故障的情况下，正常的霍尔跳变沿仅有2个，与单霍尔故障相比，跳变沿丢失了一倍。若h2和h3双霍尔故障发生后，则需在丢失跳变沿的前一个跳变沿tn处分别估算出与tx和ty处丢失的2个跳变沿之间的时间间隔，分别记为τ1和τ2。时间间隔τ1对应的位置间隔仍然为Δθx=π/3，而时间间隔τ2对应的位置间隔为Δθy=2π/3，其计算式为

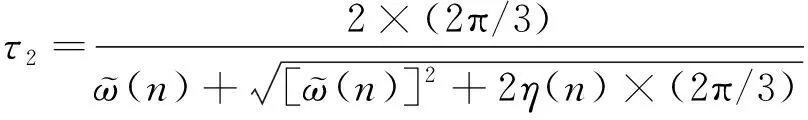
(15)

通过式(14)和式(15)可估算出时间间隔τ1和τ2，建立双霍尔故障下的插值表，如表3所示。

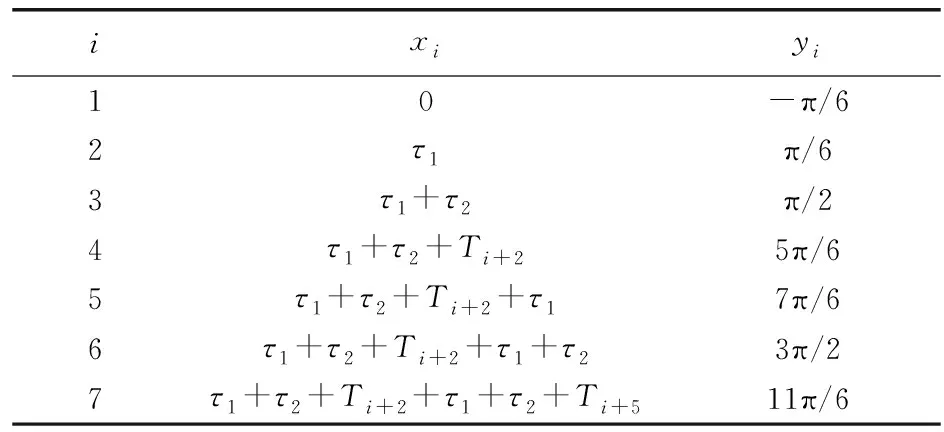
表3 双霍尔故障插值坐标表

通过控制器诊断当前霍尔传感器故障类别，利用剩余正常霍尔传感器重新建立插值坐标，重构单霍尔故障及双霍尔故障的最小二乘法二次多项式。利用该容错控制方法可缩短容错时间及削弱机械安装导致霍尔传感器磁极检测偏差对位置估算的影响。

4 试验平台搭建与试验结果分析

为了验证上文提出的霍尔传感器故障诊断方法的有效性及故障霍尔传感器容错控制的可行性，搭建了BLDCM控制系统的试验平台，由BLDCM、控制器、驱动器、直流电源及台架组成。通过TMS320F28335实现电机驱动算法、霍尔传感器故障诊断及容错控制，利用示波器和Labview开发的上位机软件进行数据采集。BLDCM主要参数如表4所示。BLDCM控制系统试验平台如图5所示。

表4 BLDCM主要参数

图5 BLDCM控制系统试验平台

图6(a)、图6(b)分别为单霍尔传感器故障及双霍尔传感器故障的波形图。由图6(a)可知，霍尔传感器h1在68 ms时出现故障，控制器对故障霍尔传感器进行诊断后，切换成容错控制，75 ms恢复至正常波形。当霍尔传感器h1和h3分别在32 ms和38 ms处出现故障时，电流波动时间比单霍尔故障持续时间更长；诊断出故障后切换至容错控制，在42 ms时A相电流波动较明显，52 ms恢复至正常波形。试验结果表明故障诊断后系统能够快速切换至容错控制，并迅速恢复至正常状态。

图6 单相及两相霍尔传感器故障

图7(a)为电机在750 r/min正常运行的转子位置曲线，未出现明显转速波动。图7(b)为霍尔传感器h1有故障的转子位置曲线，霍尔传感器h1在88 ms处出现故障，转速波动约为15 r/min，在95 ms处恢复至正常。图7(c)为霍尔传感器h1和h3故障时的转子位置曲线，2个霍尔传感器分别在82 ms及87 ms处出现故障，转速波动约为25 r/min，经过故障诊断及容错控制后，102 ms处位置曲线恢复至正常。试验结果验证了基于最小二乘法的容错控制方法能较好地克服因机械安装导致霍尔传感器磁极检测偏差对位置估算的影响。

图7 转子位置曲线

图8为电机空载情况下的相电流和线电流波形。图8中，相电流为正弦波，线电流经滤波后为马鞍波，验证了电机在矢量控制方式下能正常运行。图9(a)和图9(b)分别为霍尔传感器h1和h3在故障时的加减负载试验的相电流波形。从图9可以看出，电流波动较小，验证了转子估算位置与转子真实位置偏差较小，系统稳定性较强。

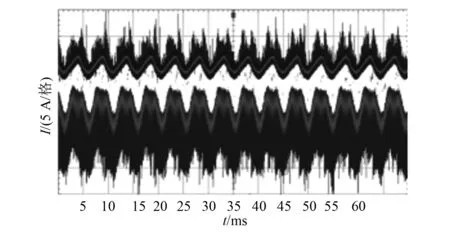
图8 电机正常运行A相相电流和AB相线电流

图9 电机加减负载相电流

5 结 语

本文提出了一种基于最小二乘法的BLDCM霍尔传感器故障诊断及容错控制的方法。在BLDCM加载平台上验证了该算法的正确性和有效性，得出以下结论：

(1) 基于最小二乘法与一阶泰勒位置估算比较的诊断方法，能够快速、有效地对霍尔传感器进行实时诊断。

(2) 基于最小二乘法的容错控制方法，对故障下丢失的跳变沿时间进行重构，重新获得最小二乘法拟合曲线，对转子位置进行估算。可以有效克服因机械安装导致霍尔传感器磁极检测偏差对位置估算的影响。

综上所述，本文提出的霍尔传感器故障诊断与容错控制策略可应用于BLDCM矢量控制系统。