既有建筑抗震鉴定可变荷载取值修正研究
2021-03-12游剑龙
游剑龙
(福建博海工程技术有限公司 福建福州 350001)
0 引言
随着我国城镇化建设的发展,大中城市市区内的新建用地已日趋减少,土地利用率逐渐饱和,可供建的建筑用地越来越少,大量既有建筑占比大幅提升[1]。我国现行抗震设计规范根据当前使用情况进行了及时修编,依据旧的抗震设计规范修建的既有建筑未必满足现行抗震鉴定标准的要求。因此,对既有建筑进行科学、合理的抗震鉴定,提出经济有效的维修、加固、改造或更新的技术对策,尤为必要。
在建筑结构设计基准期内,可变荷载取值具有较大的随机性,在荷载规范[2]中定义可变荷载取值应采用最大荷载概率分布函数进行计算。显然,可变荷载取值与建筑设计基准期有关,不同的建筑设计基准期其可变荷载取值也必然不同[3]。在鉴定标准[4]引入了后续使用年限的概念,由于该规范的局限性,并没有给出既有建筑不同后续使用年限下可变荷载取值标准,因此对既有建筑不同后续使用年限内可变荷载取值标准的研究,具有十分重要的工程实际意义。不少学者针对建筑结构可变荷载取值做过一系列研究[5-8],但对既有建筑进行抗震鉴定时,需对可变荷载取值进行修正的研究相对较少。
本文以工程常见的楼面活荷载、风荷载、雪荷载为研究对象,在荷载取值保证率一致的情况下,结合极值Ⅰ型分布及等超越概率原则,推导出不同后续使用年限内对既有建筑进行抗震鉴定时可变荷载取值修正系数。以福建某教学楼为工程实例,对比分析可变荷载按现行荷载规范取值及按推导出的修正系数取值鉴定结果的异同,为类似既有建筑抗震鉴定提供技术借鉴。
1 确立既有建筑后续使用基准期
活荷载一般以年最大值随机变量进行统计分析,从而得到活荷载的年最大值概率分布。如图1所示,T1年一遇活荷载在结构设计基准期n年内的超越概率为[9]。
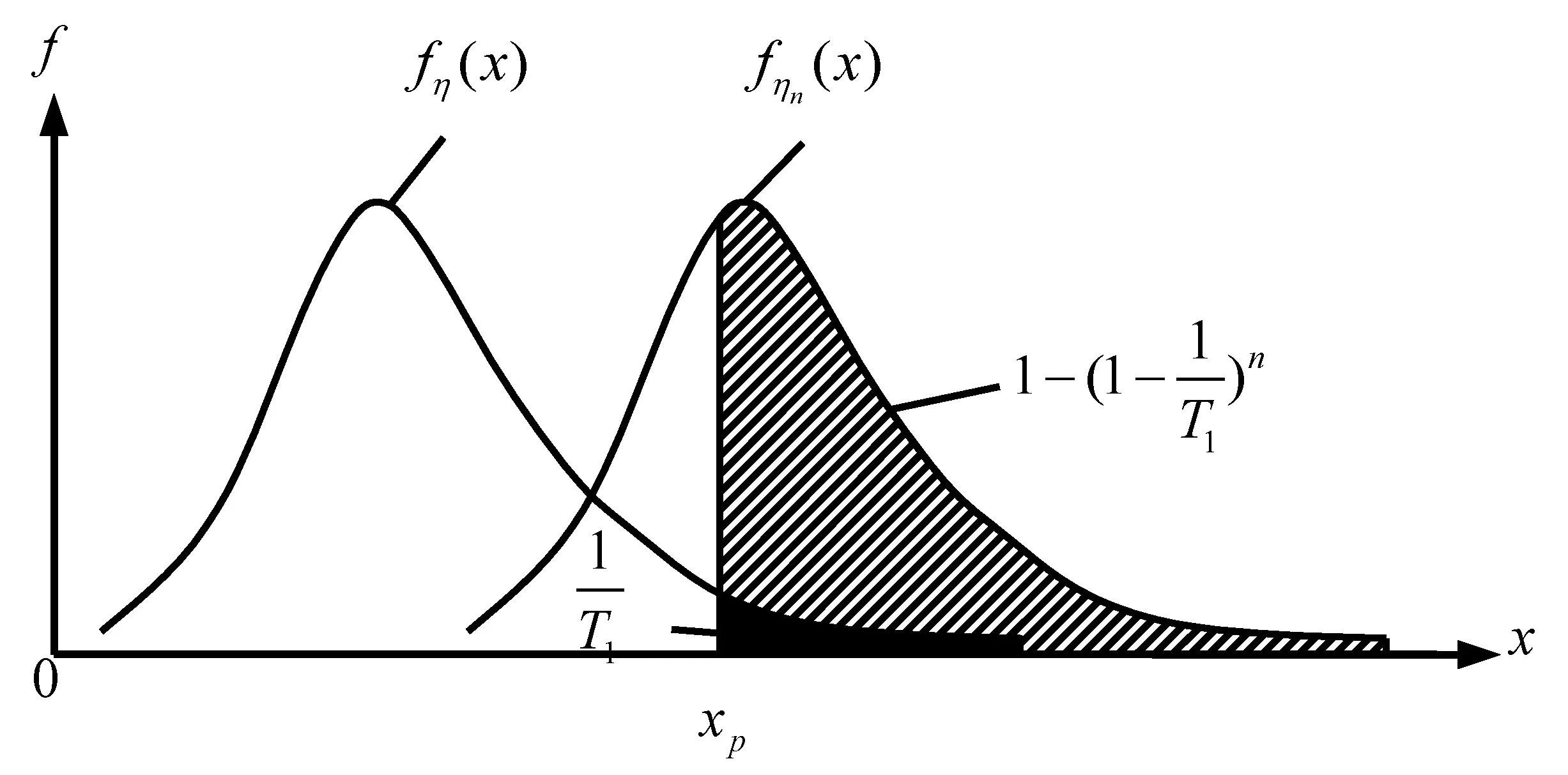
图1 T1年一遇活荷载结构设计基准期n年内超越概率

(1)
T2年一遇活荷载既有建筑后续使用年限年m年内的超越概率为:
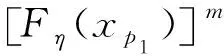
(2)
由等超越概率原则可知[9]:结构设计使用期n年内的超越设计荷载概率等于既有建筑后续使用年限m年内的超越评估荷载概率。联立式(1)及式(2)得:
(3)
将式(3)进行数学变换得:
(4)
式中:
n——结构设计使用年限;
T1——结构设计使用基准期;
m——结构后续使用年限;
T2——结构后续使用基准期。
由现行荷载规范可知,建筑结构设计使用年限n及结构设计使用基准期T1均为50年。代入式(4)可得T2≈m,即既有建筑后续使用基准期近似等于既有建筑后续使用年限。
2 既有建筑可变荷载取值修正
2.1 既有建筑楼面活荷载取值修正
我国在20世纪七八十年代,通过对楼面活荷载进行统计调查及分析,得到建筑结构楼面活荷载任意时点概率分布函数服从极值I型分布[10],因此既有建筑后续使用基准期T2内楼面活荷载概率分布函数也服从极值Ⅰ型分布。由极值I型分布的特点知:既有建筑后续使用基准期T2内活荷载L的平均值和标准差与既有建筑任意时期活荷载L分布的平均值和标准差具有式(5)及式(6)函数关系,关系示意如图2所示。
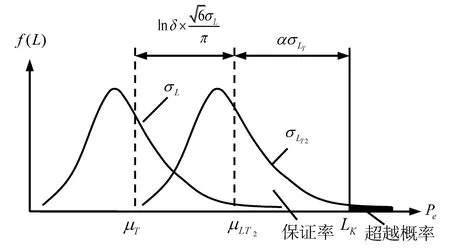
图2 任意时点最大楼面活荷载分布与后续使用基准期最大楼面活荷载分布及荷载标准值Lk之间的关系
(5)
σT2=σL
(6)
式中:
μT2——既有建筑后续使用基准期T2内活荷载L分布的平均值;
σT2——既有建筑后续使用基准期T2内活荷载L分布的标准差;
μL——既有建筑任意时期活荷载L分布的平均值;
σL——既有建筑任意时期活荷载L分布的标准差;
δ——既有建筑后续使用基准期T2内活荷载L的平均出现次数。
根据荷载规范,楼面活荷载L按其随时间变异的特点,楼面活荷载由持续性楼面活荷载Li及临时性楼面活荷载Lrs组成。表1列出了我国对楼面持续性活荷载Li和临时性活荷载Lrs的调查统计和分析的结果。表中任意时点楼面活荷载,对于办公楼、住宅系10年时段最大楼面活荷载,对于商场系1年时段最大楼面活荷载,因而不同结构后续使用基准期内活荷载的平均出现次数δ如表2所示。
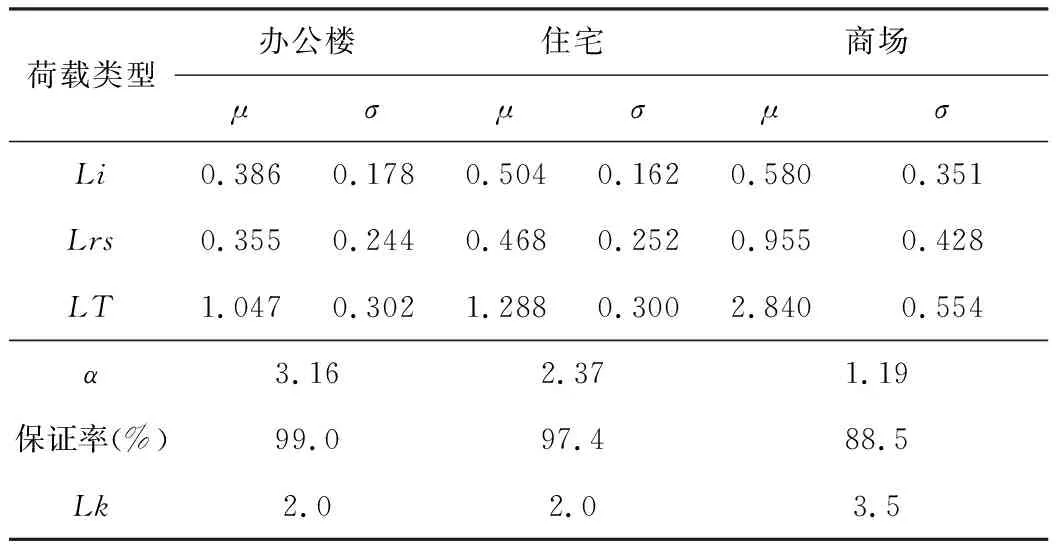
表1 楼面活荷载统计调查及分析结果 kN/m2
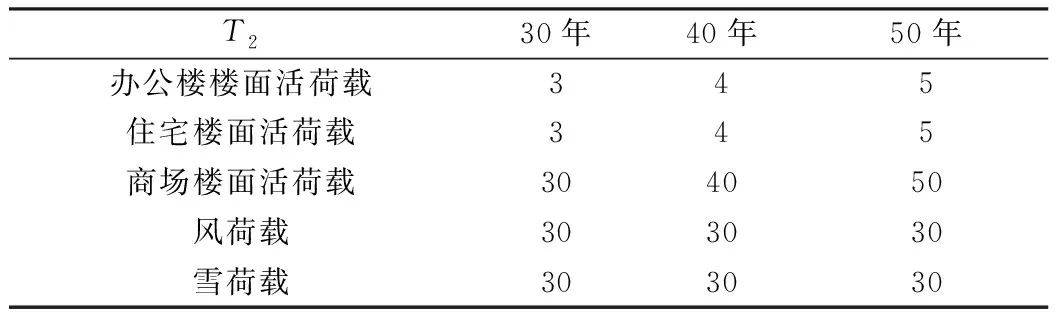
表2 后续使用基准期内活荷载的平均出现次数δ
根据Turkstra 组合规则[11],后续使用基准期T2内的最大楼面活荷载LT2,由任意时点持续性楼面活荷载LiT2与后续使用基准期T2内的最大临时性楼面活荷载LrT2相组合得到,即:
μLT2=μLiT2+μLrT2
(7)
(8)
在荷载保证率一致的情况下,由公式(5)~(8)及表1和表2可得到L30及L40楼面荷载取值如表3所示,关系示意如图3所示。

表3 既有建筑L30及L40楼面荷载取值结果(kN/m2)

图3 既有建筑不同后续使用基准期使用年限最大活荷载分布及其标准值的关系(Pe—超越概率)
令α=LT2/LK可得既有建筑不同后续使用基准期T2内楼面活荷载标准值的修正系数α,如表4所示。

表4 既有建筑楼面活荷载标准值修正系数
2.2 风荷载与雪荷载取值修正
风荷载与雪荷载是工业与民用建筑一种重要的外部荷载。由超越概率原则可知,建筑结构设计基准TS内发生超越荷载概率与既有建筑后续基准期T内发生超越荷载概率一致[3],即:
FQ,Ts(QTs,k)=FQ,T(QT,k)
(9)
式中,FQ,Ts,FQ,T分别为TS结构设计使用期及T结构后续基准期下风荷载及雪荷载最大值概率分布函数;QTs,k,QT,k分别为TS结构设计使用期及T后续基准期下风荷载与雪荷载标准值。
据年最大风荷载及雪荷载资料统计分析可得,年最大风荷载及雪荷载概率分布均可用以下极值I型分布函数表示。
pk=FQ(Qk)=exp{-exp[-α(Qk-β)]}
(10)
(11)
(12)
式中:
μQ——风荷载及雪荷载年最大值概率分布的平均值;
σQ——风荷载及雪荷载年最大值概率分布的标准差;
Qk——风荷载及雪荷载标准值;
δ——重现期。
令QTs,k/QT,k为既有建筑后续使用基准期Ts内基本风荷载及雪荷载修正系数,风荷载修正系数用β表示,雪荷载修正系数用γ表示。由式(11)、式(12)及表2,可得既有建筑不同后续使用基准期内基本风荷载及雪荷载修正系数,如表5所示。

表5 既有建筑基本风荷载及雪荷载修正系数
3 工程实例
3.1 工程概况
福建某小学教学楼为3层钢筋混凝土结构,总建筑面积约990m2,层高3.3m,楼盖及屋盖均为现浇钢筋混凝土结构,房屋总高度为10.1m,基础采用柱下条形基础。该工程地处抗震设防烈度7度区(0.1g),抗震设防类别为重点设防类(乙类),约于1985年施工建成,已投入使用31年,为了解本工程的结构安全状况,需对其进行抗震鉴定分析。经现场检查,柱尺寸为490 mm×370 mm,主梁尺寸为200 mm×500 mm,次梁尺寸为50 mm×300 mm,各层墙体均设置闭合圈梁。楼梯间设在5轴及6轴之间。项目实景图如图4所示,结构平面图如图5所示。

图4 建筑实景图
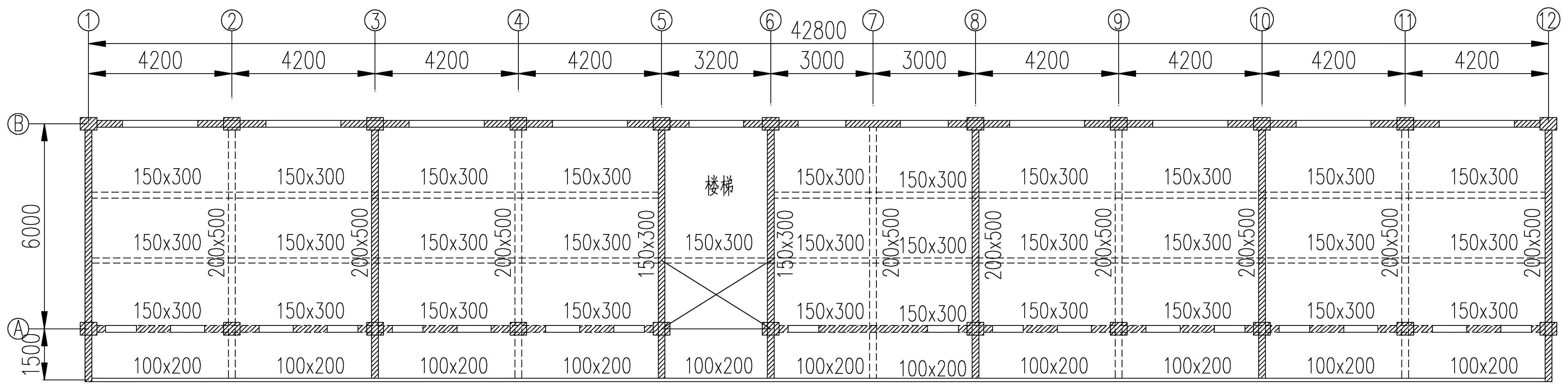
图5 建筑结构平面图
3.2 抗震鉴定
该项目抗震设防类别为重点设防类(乙类),根据鉴定标准要求,后续使用年限按30年考虑(A类建筑),该框架抗震等级为三级。
3.2.1抗震措施鉴定(第一级鉴定)
第一级鉴定结果如表6所示,房屋层数、结构体系、构件连接的可靠性、混凝土强度均满足鉴定标准要求,但部分构件纵向钢筋和横向钢筋配筋设置不满足鉴定标准要求,需要进行第二级鉴定,判定结构的抗震性能。

表6 第一级鉴定结果
3.2.2抗震承载力验算(第二级鉴定)
根据建筑现场检测数据及现场绘制布置图,本文采用MIDAS GEN进行结构承载能力验算分析,建筑计算模型如图6所示。
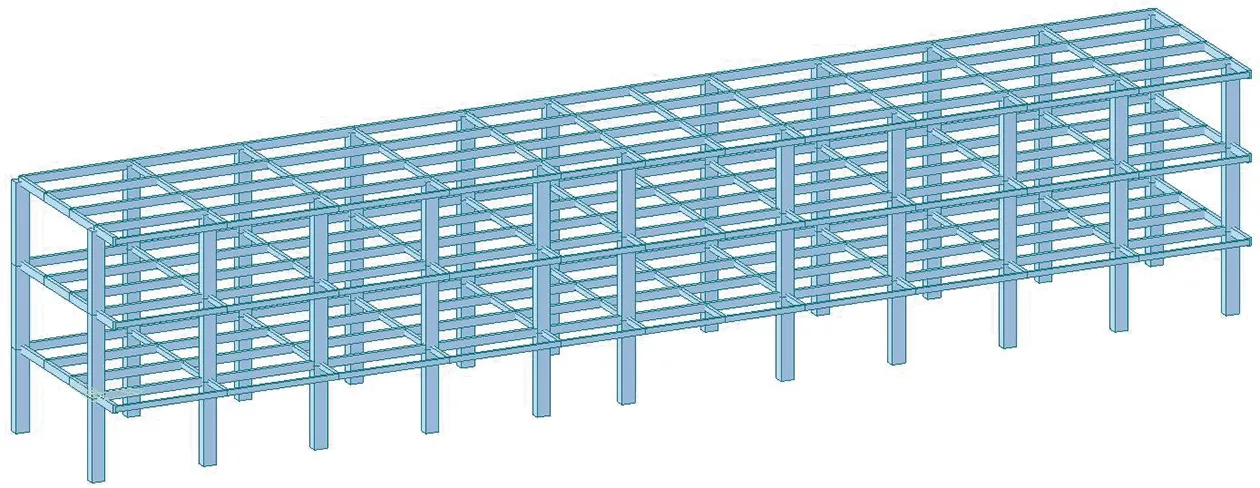
图6 建筑计算模型示意
3.2.3荷载参数取值
建筑结构安全等级取二级,结构重要性系数r0取1.0。恒载按实际板厚取值,装修荷载为1.2kN/m2。办公室活荷载为2.0kN/m2,教室及卫生间活荷载为2.5kN/m2,走廊及楼梯活荷载为3.5kN/m2,不上人屋面活荷载为0.5kN/m2。风荷载W0为0.55 kN/m2,雪荷载S0=0.20 kN/m2。
3.2.4根据推导出的修正系数取值
该项目既有建筑后续使用基准期为30年,采用表4及表5修正系数对现行规范荷载中楼面活荷载、风荷载及雪荷载进行修正。
3.2.5验算结果分析
该项目分别按现行规范荷载及推导出的修正系数,对楼面活荷载、风荷载及雪荷载取值进行抗震验算。按现行规范荷载取值计算的结果如表7所示,按按推导出的修正系数取值的计算结果如表8所示。二者计算的框架柱及抗震墙轴压比均满足现行规范要求,但按现行荷载标准取值验算的框架柱、梁配筋不足数量多于按推导出的修正系数取值验算所得的数量。因此,该类既有建筑对可变荷载取值进行修正,能更加科学、合理的反映结构的真实抗震情况,也便于业主采用最为经济可靠的维修加固对策。故,对既有建筑后续使用基准期内进行抗震鉴定时,可变荷载取值有必要按现行荷载标准结合本文推导出的修正系数进行修正。

表7 按现行规范荷载取值构件配筋不足计算结果
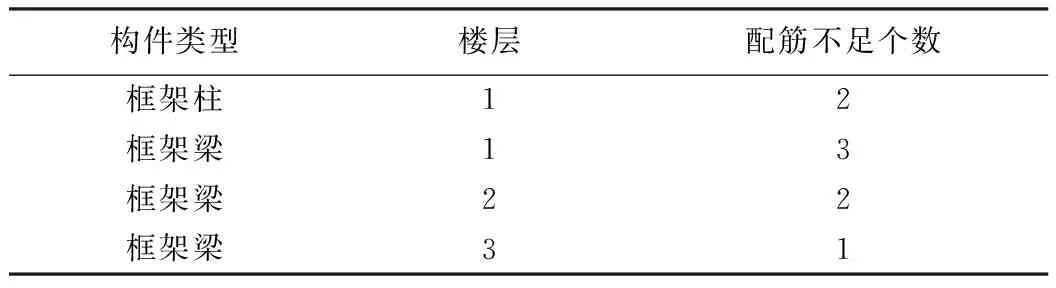
表8 按推导出的修正系数取值构件配筋不足计算结果
4 结论
本文以可变荷载作为研究对象,在荷载取值保证率一致的情况下,结合极值Ⅰ型分布及等超越概率原则,推导出不同后续使用年限内对既有建筑进行抗震鉴定时可变荷载取值修正系数。以福建某教学楼为工程实例,对比分析了可变荷载按现行荷载规范取值及按推导出的修正系数取值的鉴定结果,研究结果表明:
(1)在既有建筑与新建建筑具有相同的安全储备,及荷载取值保证率一样的情况下,可变荷载取值修正后计算的结果较未修正前,结构配筋需求量较小。
(2)相比现行规范可变荷载标准取值,利用本文推导出的可变荷载修正系数进行既有建筑抗震鉴定,能更加科学、合理地反映结构的真实抗震情况。
因此,在对既有建筑进行建筑抗震分析时,应结合项目后续使用基准期根据本文推导出的荷载修正系数进行荷载取值的修正。
