前伏不同角度富水溶洞下节理隧道最小防突层厚度研究*
2021-03-11舒佳军邓正定黄晶柱
舒佳军,邓正定,黄晶柱
(江西理工大学 土木与测绘工程学院,江西 赣州 341000)
0 引言
溶洞突水是隧道施工的主要灾害之一,2006年,由于多日降雨,宜万线马鹿箐隧道地下溶洞水压超过临界水压,围岩失稳并发生涌水,最大涌水量达到30 000 m3/h[1];奥斯陆海湾在海底施工中提前预测到前方存在突水隐患,避免事故的发生[2]。
在开挖扰动和高压水力劈裂作用下,隧道岩体中的节理尖端应力集中,使节理尖端起裂、扩展,引起溶洞水沿节理通道涌出从而造成突水事故。因此,准确预测开挖掌子面防突层安全厚度对避免隧道突水事故有重要意义。针对掌子面防突层安全厚度,近年来相关学者进行较多研究,并提出相应的计算方法。李术才等[3-4]基于断裂力学分析,针对防突层厚度提出“两带”理论并据此推导出爆破开挖扰动与水压共同作用下的岩层最小厚度公式,然后又将岩溶隧道围岩最小安全厚度分为扰动区厚度、完整岩体保护区厚度和开挖岩体破坏区厚度,并总结性地提出不同类型突水发生的条件、围岩失稳判据及最小安全厚度分析方法;郭佳奇等[5]基于弹性板理论分别探讨简支与固支下的岩层失稳临界厚度;马永昌[6]依托高铁岩溶隧道,运用GTS模拟不同工况,得出隧道安全距离与溶洞体积成正比关系;姚海波等[7]基于数值模拟方法对龙泉山隧道掌子面围岩进行分析,发现隧道掘进扰动使围岩应力产生重分布,进而对最小防突层厚度产生影响;Yang等[8]基于H-B非线性破坏准则,采用极限分析理论和上限定理,并结合变分原理,推导出岩层最小厚度的表达式。
针对防突层厚度的已有研究,多数学者将富水溶洞置于开挖隧道正前方来分析,忽视溶洞可能存在于与隧道水平轴线不同夹角处位置。综上所述,本文基于断裂力学和弹性力学,分析溶洞方位角不同时节理岩体在静水压力和开挖扰动共同作用下翼裂纹应力强度因子及扩展长度的变化关系,得到隧道围岩掌子面最小防突层厚度的计算方法,为相关隧道工程的安全施工提供借鉴。
1 节理隧道最小防突层厚度分析
1.1 含水节理翼裂纹扩展模型
文献[9]认为含水节理围岩破坏形式主要是压剪扩展破坏。在研究围岩断裂面上的应力时,常取原岩地应力作为节理面法向应力和切应力的计算依据,但由于开挖隧道引起地应力重分布,将重分布应力作为节理面法向应力和切应力的计算依据更符合实际。故做出如下2个假设:1)模型满足线弹性断裂力学;2)溶洞中水压力为恒定的静水压力。
按照弹性理论中的基尔希公式[10]可以求出围岩任意一点处应力值,如式(1)~(3)所示:
(1)
(2)
(3)
式中:σr为径向应力,MPa;σθ为周向应力,MPa;τrθ为切应力,MPa;σ1为水平方向地应力;σ3为竖直方向地应力,MPa;a为隧道开挖断面半径,m;r为隧道中心至微元体径向距离,m;φ为极坐标下自水平轴线算起的角度,(°)。
由式(1)~(3)可知,围岩各点应力值随r和φ变化而变化,使计算节理面上应力较为复杂,借鉴Mark[11]对不均匀分布裂纹的表面力求解,将节理面上各点不同应力值用平均应力来代替。据此建立节理应力计算模型,如图1所示,其中,β为裂纹倾角,(°);b为节理裂纹半长值,m。

图1 节理应力计算模型Fig.1 Calculation model of joint stress
用节理面上积分中值应力值作为其平均应力,将裂纹与溶洞相交点作为积分起点,另一端点作为积分终点进行积分,如式(4)~(6)所示:
(4)
(5)
(6)
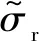
将极坐标系下的平均径向应力、平均周向应力和平均切应力转换为Cartesian坐标系下的σx,σy和τxy,如式(7)所示:
(7)
根据式(7)并考虑静水压力在节理面产生的法向力,得到斜截面上正应力σβ(取压为正)和剪应力τβ,如式(8)所示:
(8)
式中:p为溶洞静水压力,MPa。
节理断面受到压、剪复合作用时,节理面分别受到法向应力作用和剪应力作用,剪应力驱动节理面滑移,法向应力产生的摩擦力阻止滑移,故节理面有效剪应力τeff如式(9)所示:
τeff=〈τβ-μfσβ〉
(9)
式中:μf为节理面摩擦系数;符号“〈〉”表示通常的McCauley括弧,若x>0,〈x〉=x,若x<0,〈x〉=0。
较多学者对节理面压剪破坏模式进行分析和试验,文献[12]认为围岩节理面破坏多为节理端部翼裂纹的扩展贯通直至围岩失稳破坏,隧道围岩节理在开挖扰动和溶洞水压共同作用下,端部翼裂纹的应力强度因子会增大。当翼裂纹尖端应力强度因子大于围岩的断裂韧度时,翼裂纹便沿着某个方向开始起裂扩展。将处于临界状态时的翼裂纹扩展长度作为计算最小防突层厚度(即临界厚度)的依据。
1.2 翼裂纹应力强度因子变化规律
Horii和Nemat-Nasser[13-14]用复变函数得出翼裂纹的应力强度因子KI的近似解,如式(10)所示:
(10)
式中:σn′为翼裂纹扩展界面法向应力,MPa;θ为翼裂纹扩展界面起裂角,(°);l为翼裂纹扩展长度,m;l*为模拟翼裂纹未扩展时引入的当量裂纹长度,大小为0.27倍半节理长度,m。
用翼裂纹扩展界面上主应力σl和方向角θl代替σn′和θ,得到修正后的KI近似解,如式(11)所示:
(11)
式中:σl为翼裂纹扩展后的主应力值,MPa;θl为翼裂纹的扩展方向角,(°)。
当翼裂纹应力强度因子大于岩体断裂韧度时,节理端部发生扩展,随着节理端部翼裂纹扩展长度的增大,尖端应力强度因子逐渐减小,直至小于断裂韧度,翼裂纹停止扩展。借鉴文献[5]中算例的参数,节理岩体受到的远场应力σ1为40 MPa,σ3为5 MPa,节理面摩擦系数为0.35,围岩节理长度为1.35 m,节理倾角为30°。取隧洞开挖半径为4 m,富水溶洞等效半径为2 m,开挖隧洞中心至溶洞节理端部水平距离8 m,岩体断裂韧度KIC=4 MPa·m0.5。将上述参数代入式(11),得到翼裂纹尖端应力强度因子KI与溶洞方位角φ的变化规律,如图2所示。

图2 应力强度因子随溶洞方位角变化规律Fig.2 Variation of stress intensity factor with azimuth angle of karst cave
由图2可知,当溶洞方位角增大时,翼裂纹应力强度因子曲线出现2个波峰,其整体变化趋势是先增大后减小,峰值出现在溶洞方位角为30°处。观察翼裂纹扩展长l=0 m的KI-φ曲线,发现溶洞方位角为0°时节理端部翼裂纹应力强度因子为1.272 MPa·m0.5,小于开挖隧道围岩的断裂韧度,不会出现翼裂纹萌生,而溶洞方位角为10°时KI则为6.918 MPa·m0.5,节理端部会萌生翼裂纹进而发生扩展。同时发现溶洞方位角大于20°时,不同扩展长度下的翼裂纹应力强度因子离散程度很小,当方位角较大时,翼裂纹应力强度因子随扩展长度增大而减小的幅度较小,使翼裂纹有保持继续扩展的能力。
2 最小防突层厚度
2.1 掌子面最小防突层厚度的组成
文献[3]将岩溶隧道掌子面最小安全厚度划分为损伤带和水力劈裂带,通过对围岩开挖扰动的研究[15]及本文对节理端部翼裂纹扩展的分析,将防突层厚度分为2部分,第1部分为隧道施工造成的扰动带厚度,记为Le;第2部分为原生节理和节理扩展二者累加得到的节理带厚度,记为Lc。节理带厚度Lc也分为2部分:1)原生节理带厚度Lc1,由于围岩存在天然节理,周边岩体强度较低,抵抗破坏能力较弱,岩层易破碎,这种初始存在的原生节理带在工程中已经被证实,宜万线铁路八字岭隧道DK108+721~731段和齐岳山隧道DK362+060处溶洞发育,岩层发生破碎形成节理带[16];2)节理扩展带厚度为Lc2,由于开挖扰动和水力劈裂共同作用使翼裂纹不断扩展,扩展阶段节理端部岩体强度降低,致使翼裂纹易扩展贯通并导致围岩失稳破坏。最小防突层厚度组成示意如图3所示。

图3 最小防突层厚度组成示意Fig.3 Schematic diagram for composition of minimum anti-outburst layer thickness
翼裂纹处于临界状态时KI=KIC,此时翼裂纹扩展长度为扩展临界长度,将扩展临界长度记为lc,代入到式(11)得式(12):
(12)
将式(12)中等式右边第1部分用幂级数展开并取前2项,得到lc,如式(13)所示:
(13)

故节理带厚度Lc计算如式(14)所示:
Lc=Lc1+Lc2=2bcosβ+lccos(β-θl)
(14)
2.2 最小防突层厚度计算方法
由图3可知,节理隧道掌子面最小防突层由2部分共3段厚度组成,各段厚度之和最小值即为掌子面防突层临界厚度值Lmin,计算如式(15)所示:
Lmin=Le+Lc=Le+Lc1+Lc2
(15)
其中扰动带厚度Le的存在通常是由于开挖过程中爆破对前方围岩产生扰动作用造成的,文献[15]依托普济隧道3种不同爆破方法的研究发现,爆破作业对开挖掌子面前方岩体的最小扰动深度为0.87 m,最大扰动深度则为1.45 m,考虑到安全储备和经济,可适当增大扰动带厚度,故扰动带厚度Le取1.50 m;将扰动带厚度和节理带厚度代入式(15),得到围岩掌子面最小防突层厚度Lmin,如式(16)所示:
Lmin=1.5+2bcosβ+lccos(θl-β)
(16)
通过上述算例,得到掌子面防突层临界厚度与溶洞方位角(Lmin-φ)变化关系并绘制相应曲线,如图4所示。

图4 临界厚度随溶洞方位角变化曲线Fig.4 Variation of critical thickness with azimuth angle of karst cave
由图4可知,不同溶洞方位角对掌子面临界厚度的影响较大。当方位角为0~20°时临界厚度增长缓慢,当方位角继续增大,临界厚度增长迅速后又较快地减小到初始厚度值,并在30°时临界厚度达到峰值6.268 m,原因是在扰动带厚度和原生节理带厚度不变的情况下,翼裂纹扩展厚度是最小防突层厚度的决定因素;算例中溶洞方位角为30°时,节理面上有效剪应力较其他方位角下更大,其翼裂纹初始应力强度因子相对也更大,又因其随扩展长度增大而降低幅度较小,造成方位角为30°时节理端部翼裂纹扩展长度更大,因此掌子面临界厚度峰值出现在溶洞方位角为30°时。
3 最小防突层厚度参数影响分析
由式(8)、式(13)和式(16)可知,含水节理隧道开挖掌子面最小防突层厚度与节理倾角、节理长度、掌子面开挖半径等参数有关。分别研究不同参数对最小防突层厚度的影响,当讨论某项参数时,其他参数取定值,只改变此参数,并通过式(16)得到相应的防突层临界厚度随参数变化的曲线。
3.1 节理倾角对防突层厚度的影响
临界厚度随节理倾角变化曲线如图5所示。

图5 临界厚度随节理倾角变化曲线Fig.5 Variation of critical thickness with joint dip angle
由图5可知,当溶洞方位角在0~15°内增大时,不同倾角下的临界厚度变化曲线增长缓慢,当溶洞方位角大于15°时,临界厚度迅速增大到峰值后又开始减小,如倾角为0,30,60°时临界厚度出现在方位角为30°附近,倾角为90°时临界厚度出现在方位角为20°,其中节理倾角为30°的临界厚度峰值大于其他节理倾角下的峰值,故认为节理倾角的增大未改变临界厚度变化的趋势,仅改变临界厚度增长幅度,原因是倾角为30°的节理翼裂纹扩展长度与倾角为0°的扩展长度之差大于二者的原生节理长度差,而与倾角为60°的原生节理长度差大于二者的翼裂纹扩展长度差;因此倾角为30°的峰值临界厚度大于倾角为0,60,90°的情况,该观点与文献[9]得到的结论一致。
3.2 节理长度对防突层厚度的影响
临界厚度随节理长度变化曲线如图6所示。

图6 临界厚度随节理长度变化曲线Fig.6 Variation of critical thickness with joint length
由图6可知,当溶洞方位角位于0~20°内时,不同节理长度下临界厚度随溶洞方位角增大均保持平缓变化,当溶洞方位角继续增大,节理长度为1 m和1.35 m的临界厚度呈先增大后减小的变化趋势,而节理长度为1.70 m和2.05 m则出现2个明显波峰,其中节理长度为1.35,1.70,2.05 m的最大临界厚度均超过6 m,但节理长度为2.05 m的临界厚度最先开始增长,最早达到峰值临界厚度,意味着节理长度会改变临界厚度随方位角变化的范围。同时发现长节理所需的临界厚度较短节理大,此2方面厚度的累加,使节理长度越大的掌子面所需防突层安全厚度也越大。
3.3 隧道掌子面开挖半径对防突层厚度的影响
临界厚度随掌子面开挖半径变化曲线如图7所示。
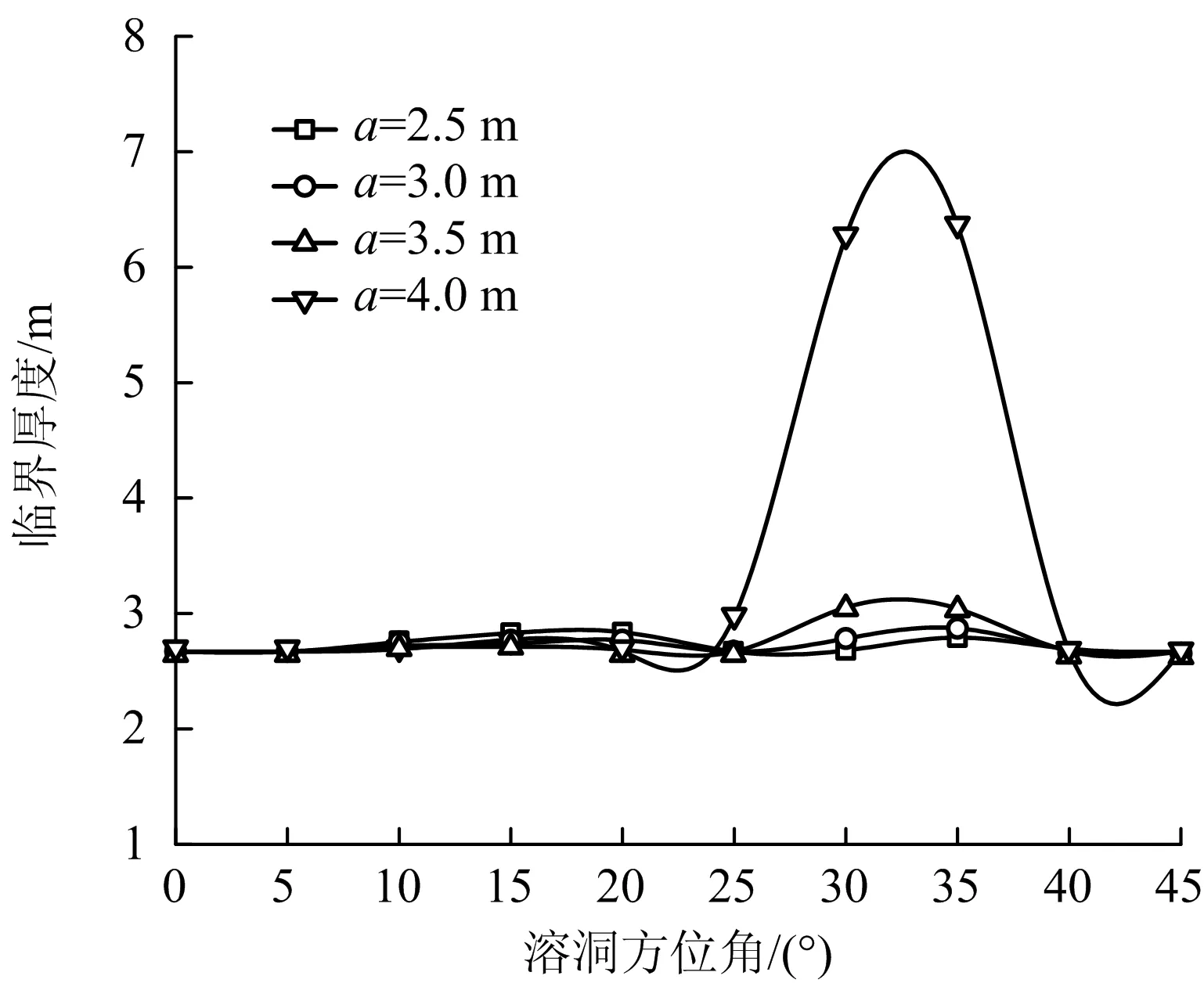
图7 临界厚度随开挖半径变化曲线Fig.7 Variation of critical thickness with excavation radius
由图7可知,当溶洞方位角在0~20°内变化时,不同开挖半径下临界厚度随方位角增大而缓慢增大,当溶洞方位角继续增大,临界厚度开始迅速增大,并在方位角为30°附近达到峰值;当方位角大于35°时,曲线开始下降。分析不同开挖半径对临界厚度影响曲线的变化规律,发现4种曲线在0~20°内高度吻合,说明在小溶洞方位角下掌子面开挖半径对临界厚度变化影响较小;而方位角为25~35°时,开挖半径对防突层厚度影响显著;随着方位角继续增大,开挖半径对临界厚度影响效果又呈减弱趋势。
4 工程实例
根据文献[17]工程资料:宜万铁路线DK245+526~245+547段为云雾山隧道,隧道处于深部孔隙带,埋深为500 m,岩层主要为含碳酸盐的灰岩层;开挖掌子面高9.8 m,宽7 m;隧道前方存在富水溶洞,静水压力实测为0.8 MPa,灰岩层中隧道围岩Ⅰ型断裂韧度为4.7 MPa·m0.5;现场测得岩层重度为26.5 kN/m3,节理倾角为15°,含水原生节理长度为1.5 m,节理面摩擦系数为0.466,围岩侧压力系数取1.5,假定开挖断面距节理端长为6 m。
由式(13)计算得翼裂纹扩展临界长度为0.293 m,将节理原生长度和开挖扰动厚度代入式(16),得到掌子面最小防突层厚度为3.235 m,而云雾山隧道现场施工现场预留岩墙厚度多为3 m。计算结果相比实际结果较为接近且增加一定的安全储备,因此本文计算方法较合理。
5 结论
1)围岩节理在溶洞高压水力作用下产生水力劈裂破坏,常表现为压剪劈裂破坏。隧道围岩节理尖端翼裂纹应力强度因子随溶洞方位角增大先增大后减小,随扩展长度的增大而减小,基于应力强度因子与断裂韧度的比较值分析围岩节理端部翼裂纹的扩展规律变化。
2)将掌子面临界厚度划分为扰动带厚度和裂隙带厚度,据此得到开挖隧道掌子面临界厚度的计算方法;初始变化阶段掌子面临界厚度随溶洞方位角增大保持缓慢增大,超过20°时临界厚度随方位角迅速增长并在30°附近达到峰值,随后临界厚度值开始减小。
3)临界厚度随节理长度的增大而增大,临界厚度随节理倾角增大初期增长缓慢,在倾角大于15°开始迅速增大,并在达到峰值厚度后开始减小;临界厚度和开挖半径的关系则取决于溶洞方位角,当方位角较大时,开挖半径对临界厚度影响显著,表现为开挖半径越大的临界厚度越大。
