城市应急物资配送路径支路限流模型研究*

宋英华，吴 坷，吕 伟

(1.武汉理工大学 中国应急管理研究中心，湖北 武汉 430070；2.武汉理工大学 安全科学与应急管理学院，湖北 武汉 430070)

0 引言

随着社会的快速发展，我国各类突发事件时有发生，对人们的正常生活产生严重的影响，可能造成重大的人员伤亡和经济损失。为最大程度地降低事故带来的人员伤亡和财产损失，灾害发生时，在规定的时间内将应急物资高效率地配送至需要的受灾点成为学者研究的重点。应急物资配送影响着整个应急环节的效率。在实际应急物资配送中，往往受到较多不确定因素的影响，比如道路的损毁，道路交通流的影响等，特别是在城市路网拥堵情况下，配送效率较容易受常态化交通的影响，故有必要研究如何保障应急物资运输的高效率。

在应急物资配送路径研究方面，国内外学者已进行大量研究，主要包括考虑需求及目标不同对应急物资配送路径影响的问题[1-5]和考虑时间约束的应急物资配送路径问题[6-9]。Hanhani[10]在研究配送网格优化时考虑时间窗的限制和多种运输方式，确定在非单一数目的应急配送中心下应对多种不同的应急资源在各受灾点之间的车辆配送路径问题；Najafi等[11]运用应急物资的目标、商品和周期等多样化的随机模型，对未服务人数、未调用车辆数和未达到的标准此3个目标函数进行分析；吕伟等[12]在研究如何提高应急物资配送效率时，建立多目标函数，以软硬时间窗为综合约束条件建立模型，最后运用遗传算法进行求解；颜瑞等[13]在研究二维装箱车辆路径问题时，考虑时间窗和多车场因素，运用量子粒子群算法和引导式局部搜索算法的混合式算法进行求解；葛显龙等[14]在研究物流配送时，针对雾霾等极端天气，引入新的碳交易机制来降低碳排放的策略，设计运用混合遗传算法来求解模型；侯玉梅等[15]以总成本最小为目标，构建带软时间窗约束的整车物流车辆路径优化问题模型，根据该模型设计对应的自适应遗传算法对该模型进行求解；王挺等[16]在研究最优应急车辆物资配送路径时，考虑震后道路车辆通行时间和道路安全性风险，将爬山算法引入遗传算法进行改进求解；杜丽敬[17]为合理地调度应急物资，研究基于多目标的单周期静态应急物资配送车辆路径问题，以“公平”为原则，以差分算法优化各个周期应急物资配送进行求解；盛虎宜等[18]考虑灾害发生初期时的资源短缺，构建单受灾点最大损失和总配送时间最少为目标的双目标应急物资配送问题，并运用二阶段混合启发式算法求解；范玉娥[19]综合考虑单车配送与多车配送的理想化情况，以运输时间与运输成本等因素建立多目标模型，综合遗传算法和爬山算法的优点来处理模型；徐浩等[20]在研究应急物资配送速度时，考虑地震对道路受损程度的影响，运用混合智能算法，验证建立在救援时的时间满意度最大和物资使用量最小的双目标优化模型。

在整个应急物资配送系统中，配送路径往往不是独立存在的，而是会受到周边相关道路的影响，其中考虑交叉口对主干路配送影响的研究较少。以往在对配送路径的研究中，缺乏考虑配送过程中多个道路的协同配送、主干配送道路间各进出口车辆限流的影响，以及配送道路实时状况不断发生变化的可能。因此，在突发事件发生后，为高效率地完成配送任务，需在短时间内考虑配送过程中支路限流对主干配送道路的影响并实时动态调整，才能更合理高效地完成配送。

本文提出的支路限流协同配送模型，是了解道路实时通行状况后，通过对道路交通交叉口支路限流的调整，快速得到1套完整的支路限流模型，使得所需的应急物资能在要求的时间窗内抵达目的地，同时保证因为路段通行管制对城市道路通行带来的影响最低。

1 问题描述

1.1 应急物资配送时间问题

应急物资配送时间指突发事件发生后，车辆按照指定配送路径完成配送任务所需要的运输时间，是评判配送路径能否满足时间窗约束的关键依据。对于某条选定的配送路径D，其运输时间T的基本计算方法如式(1) 所示:

(1)

式中:T为运输时间，h;S为路径D的长度，m;V为配送车辆的行驶速度，km/h。

此计算方法假设配送车辆沿配送路径做匀速直线运动，不符合道路交通的实际情况。

在实际道路交通流中，车辆在配送路径D上的总行驶时间(即配送时间)取决于该路径长度和车辆在该路径上的平均行驶速度和该路径的实际交通流状况，如运输道路中交叉口汇入车辆对配送道路中的交通流密度的影响等。计算方法如式(2)～(5)所示:

T=∑t

(2)

(3)

v=f(ρ)

(4)

(5)

式中：t为支路车流入口之间路段所需要的行驶时间，s；v为支路车流入口之间路段的平均行驶速度，km/h；L为支路车流入口之间路段的实际距离，km；ρ为支路车流入口之间路段上的车流密度，veh/(km·lane)；m为支路车流入口之间路段上的车道数；N为限流前支路车流入口之间路段上的车辆数；Q为支路车流入口之间路段的车辆驶出流量，veh/s；q为支路车流入口之间路段的来自主干道的车辆进入流量，veh/s；τ为支路车流入口限流的时间，s。

1.2 应急物资配送路径支路限流问题

应急物资配送路径支路限流问题是指，突发事件发生后，运输车辆在通过主干道路完成配送任务的过程中，通过对主干路所连接的各支路的限流，快速得到新的协同配送方案，使车辆完成之前在支路限流措施未干预的情况下，无法在所要求的时间内完成配送的问题。

应急物资配送示意如图1所示。在任一路网中，找到应急物资从起点P1运往终点Pn的最短路径进行配送，在整个行进过程中，共有n个道路节点，n-1段路，n-2个支路口，命名支路口为P2至Pn-1，Pc表示支路车流入口，c=1，2,…,n；Li表示支路车流入口Pc和Pc+1之间的路段的实际距离，m，i=1，2，…，n-1；Qk表示支路车流入口Pc和Pc+1之间的路段的车辆驶出流量，vel/s，k=2，…，n-1；qk表示支路车流入口Pc和Pc+1之间的路段的来自主干道的车辆进入流量，vel/s；gk表示支路车流入口的车辆进入流量，vel/s。

图1 应急物资配送示意Fig.1 Schematic diagram of emergency materials distribution

2 城市应急物资配送路径支路限流模型

2.1 模型假设

本文侧重研究突发事件下支路限流对应急物资配送路径的综合影响，考虑道路实时交通流密度对运输时间的影响，作出如下假设:

1)突发事件发生的各时间段内灾区道路状况等信息可知。

2)与主干路相连的交叉口支路双向皆可通行。

3)不考虑路口等待时间和配送往返情况。

4)物资配送车辆数目充足、运载量和单位长度运输成本一致。

5)路网完整，不存在损毁道路，且路网节点、路段距离和通达性已知。

2.2 模型构建

1)变量及符号说明

ρi表示支路车流入口Pc和Pc+1之间的路段上的车流密度，veh/(km·lane)；

mi表示支路车流入口Pc和Pc+1之间的路段上的车道数；

Ni表示限流前支路车流入口Pc和Pc+1之间的路段上的车辆数；

τk表示支路车流入口Pc限流的时间，s；

ti表示支路车流入口Pc和Pc+1之间的路段所需要的行驶时间，s；

vi表示支路车流入口Pc和Pc+1之间路段的平均行驶速度，km/h。

2)目标函数

采用谢菲尔德(Sheffield)遗传算法工具箱对上述问题进行数学建模：当突发事件发生后，首先快速收集起点至终点间的道路信息，如Pi，Li以及qk，染色体使用实数编码，染色体长度Chromlen表示限流的路口数目，染色体上每个片段对应限流的每个交叉点。对应位次的数值对应该交叉点的限流时间。

目标函数如式(6)所示：

(6)

式(6)目标函数表示限流方案影响的车辆数最小。

约束函数如式(7)～(8)所示：

(7)

(8)

式(7)表示配送车辆的总行程时间不得超过Tmax；式(8)表示任意车流入口的限流时间不得超过配送车辆行驶至该入口的花费的总时间，a为闭区间[1,n-2]上的整数。

tk，vk，ρi的计算如式(9)～(11)所示：

(9)

vk=f(ρi)

(10)

(11)

在该模型中，Li和mi是已知量，Ni，Qk，qk，gk是可观测量。

2.3 算法设计

本文通过建立城市应急物资配送路径支路限流模型，针对主干路和支干路相互协同，从而影响配送。遗传算法所采用的并行随机搜索的优化算法，能较好地解决支路与干路相互协同这一问题。

编码设计见表1。

表1 编码设计Table 1 Coding design

通过给定路段长度Li、车道数mi以及交叉路口汇入车流量gk，将交叉口限流时间赋予染色体上对应位置的数值，通过染色体的选择、交叉和变异，最后筛选适应度值Bestfit达到要求的期望值，可以得到最终随机染色体的结果，则对应的是限流时间。

使用谢菲尔德大学遗传算法工具箱，遗传操作包括选择、交叉、变异。该算法停止准则为遗传代数达到程序设置的最大迭代数，即停止运算。遗传算法流程如图2所示。

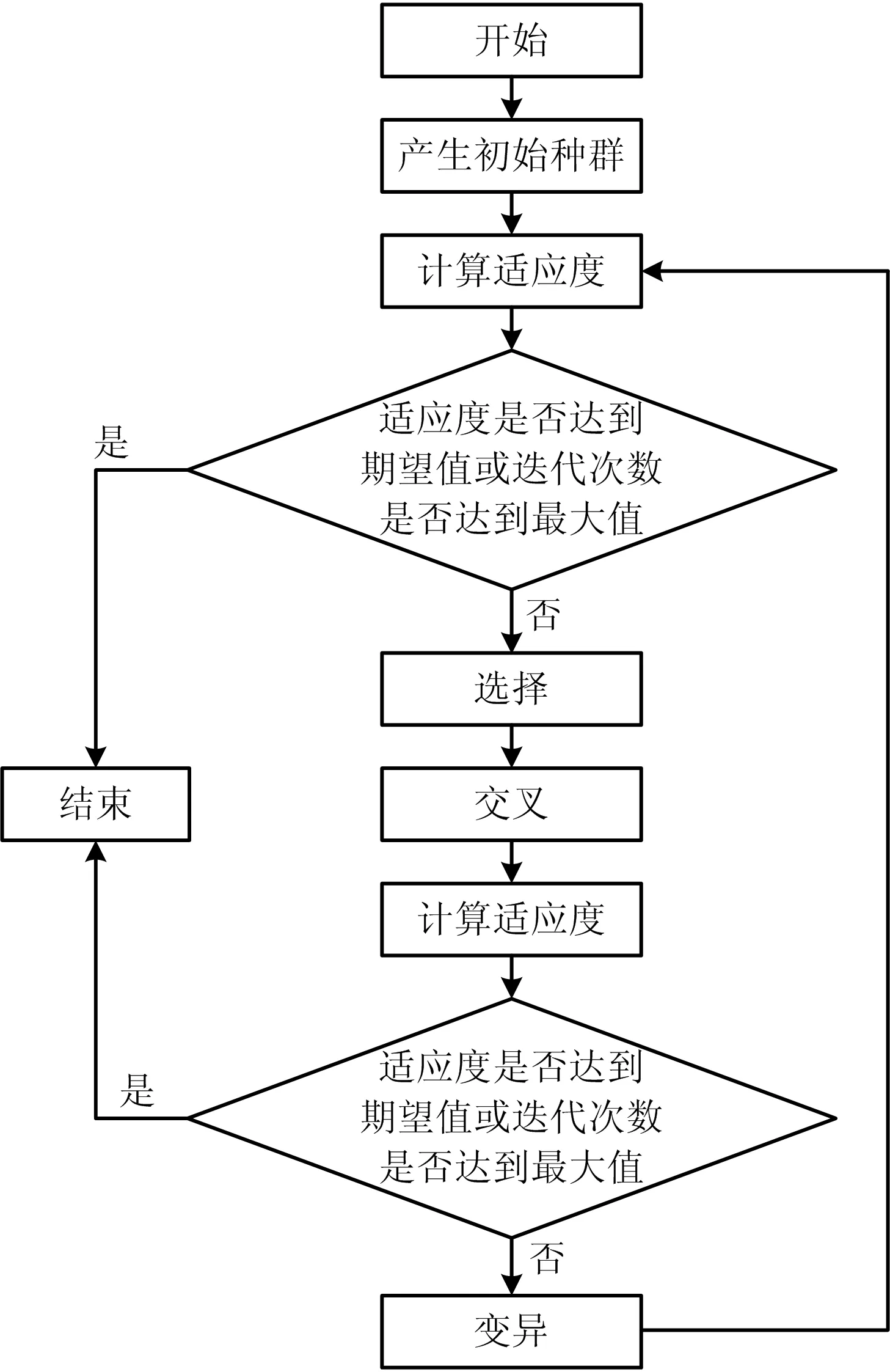
图2 遗传算法流程Fig.2 Procedure of genetic algorithm

3 情景应对分析

3.1 情景构建

假设2020年7月5日下午14∶00，因游客误食某餐厅的变质海产品，突发副溶血性弧菌食物中毒事件，需将药品尽快送达，目前有一批该类抗生素已运至某机场。突发副溶血性弧菌食物中毒情景见表2。

采用路径规划算法，可选最近主干路线进行配送。选择某机场配送至食品中毒发生餐厅的最短路线，如图3所示，然后根据该实际路网的干路和支路(匝道)信息建立拓扑图，如图4所示。

3.2 支路限流方案求解

该路段长度为24 331 m，共19个道路节点，18个路段，17个交叉口。利用测绘工具和交通部门实时监测系统，可测得每段路的实时车流量、平均通行车辆数、流入量和流出量，以及交叉路口(非主干道)的车流量。通行路段信息见表3，交叉口汇入信息见表4。

表2 副溶血性弧菌食物中毒情景简介Table 2 Brief introduction to food poisoning scenarios of Vibrio parahaemolyticus

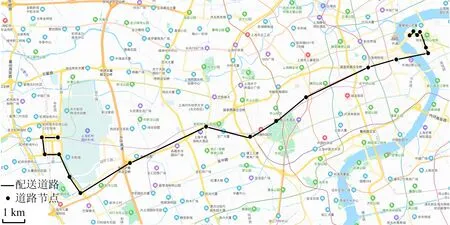
图3 实际配送路网Fig.3 Actual distribution road network

图4 干支路拓扑图Fig.4 Topology diagram of trunk road and branch road

运用MATLAB R2020a 编程进行方案求解步骤的处理，在求解目标函数时采用遗传算法(GA)进行计算，经过多次运行试验比较后设定的运行参数见表5。

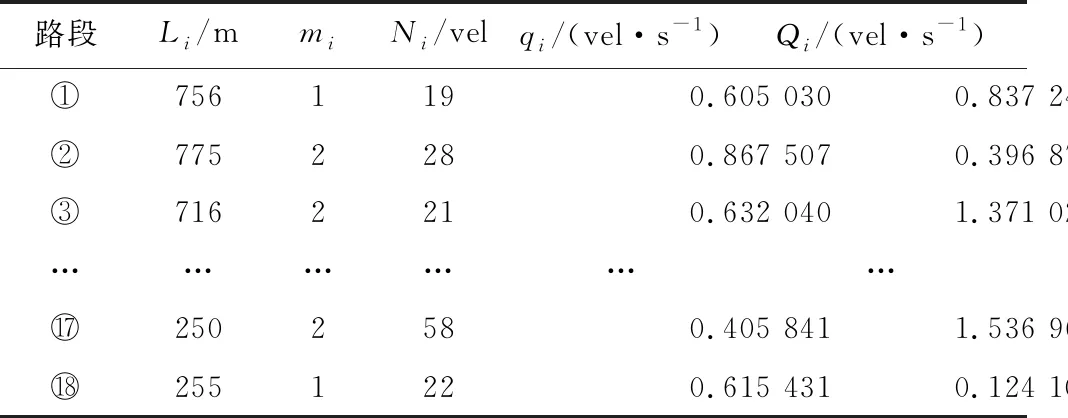
表3 通行路段信息Table 3 Information of passage road sections

迭代结果分布情况如图5所示。由图5可知，经过400次迭代后，Bestfit经过500次进化，目标函数值可收敛到最优值324，表明该结果已是稳定的最优解，即最少对城市交通324辆车产生影响，其对应的配送方案即为满足目标要求的最优配送方案，该方案显示对6号交叉口限流85 s，对10号交叉口限流95 s，限流时间见表6。

运行结果显示限流时间最少共计180 s，最少对城市交通324辆车产生影响。限流后车辆配送总时间为1 712 s，比不限流时间1 937 s节省225 s，即从约32.3 min节省到约28.5 min。运输时间达到30 min的时间窗要求。具体运行结果见表7。

表4 交叉口汇入信息Teble 4 Information of import intersection

表5 运行参数Table 5 Operating parameters

在应急物资进行配送时，通过各支路口在各时段通过限流对车辆配送路过各个路段的时间产生影响，从而得到新的车辆配送时路过各个路段的时间表，车辆通过各个路段通行时间见表8。

支路未参与限流时的配送总距离和支路参与限流时的配送总距离对比图如图6所示。由图6可知，在支路参与后，总配送距离整体比未参与限流时的距离短，可减少应急物资配送的时间成本，满足最短时间窗要求，使整个应急物流体系更加敏捷可靠且高效。

图5 迭代结果分布情况Fig.5 Distribution of iterative results

表6 交叉口限流时间Table 6 Traffic flow restriction time of intersections

表7 配送时间结果Table 7 Results of distribution time

表8 各路段通行时间Table 8 Passing time of each road section

图6 配送时间对比Fig.6 Comparison of distribution time

根据运行结果进行情景推演，得到各交叉点限流时刻和限流时间方案。结果表明车辆运输至节点5时，已用时238 s，从14∶02∶33开始对6号交叉口开始进行限流，限流85 s，结束时间为14∶03∶58，从14∶00∶00开始共计238 s；车辆运输至节点9时，已用时1 086 s，从14∶16∶31开始对10号交叉口开始进行限流，限流95 s，结束时间为14∶18∶06，从14∶00∶00开始共计1 086 s。具体方案见表9。

4 结论

1)在原有车辆路径问题基础上突破传统单目标规划对寻求最短时间路径的局限，从改变道路交通路况的角度出发，通过限制道路交叉口车辆流的方式寻求满足实际情景要求的交通管制方式和运输路线，以寻找最优可行解。

表9 交叉口限流方案Table 9 Traffic flow restriction schemes of intersections

2)将经典的LRP问题与实际道路交通通行问题相结合，从新颖的优化通行状况角度入手，摆脱传统理论模型拘泥于路径的重复选择和运输速度保持恒定的假设，更加贴近于事实情景且具有现实意义。

3)在现有的基础问题之上，将问题进一步普遍化，逐步考虑当突发事件发生时，道路实时信息不断发生变化的可能，从而将最初静态的道路交通管制问题转化为与实时信息同步变动的动态路线规划与交通管制的问题，为应急物资配送保障问题的研究提出新的思路。