基于改进模拟退火算法的社会力量救灾派遣模型*

李 莹，李 忠，张莉丽

(1.防灾科技学院 应急管理学院,河北 廊坊 065201； 2.防灾科技学院 地球科学学院,河北 廊坊 065201)

0 引言

巨大灾害的发生往往可能造成极大的人员伤亡和财产损失。但由于受灾区域自然环境、地质条件、人文生态等因素影响，导致政府救援工作出现人力短缺、救助不及时等问题[1]。随着我国经济的发展和社会的进步，越来越多的社会力量参与到灾后的救援工作中[2]。据统计,汶川地震发生后，中国红十字会征集志愿者18万人，四川各级团委登记的志愿者达到118.5万人,共向灾区派出志愿者150.85万人次[2]。但社会力量人员数量、技术能力、财物状况、位置信息等均未知，往往造成救援的无信息、无秩序、无调度、无管理的“四无”混乱状态，有时甚至“帮倒忙”。不同的灾害需要不同的救援技能，如在洪水灾害救援中，需要具备游水、高空绳索救援和操作皮划艇等能力。所以需要根据受灾情况派遣具备相应能力的社会组织，以达到救援效率最高和救援效益最大。

针对灾后救援中存在的问题，我国学者进行大量研究。其中1个重要课题是如何合理地调配救援力量，这是提高救援效率、减少人员伤亡的重要途径[3]。科学地分析灾区救援力量的需求，并合理地派遣队伍，才能以最少的救援资源达到最大程度的救援效果[4]。目前，国内外学者对此进行大量研究：Friedrich等[5]开发决策支持系统用于营救地震灾后幸存者，在该系统中可以根据灾情设计最佳搜救路线；Mike等[6]根据 Arcgis 中的路径成本矩阵分析功能，设计火灾救援调度的最优化方案；袁媛等[7]以救援任务胜任程度和时间满意度为目标函数建立模型，将双目标模型转化为单目标模型，并用匈牙利法求解得出最优派遣方案；梵治平等[8]针对突发事件应急救援人员分组问题，以救援效果为目标，构建救援人员分组模型；张雷等[9]根据灾后的需求分析，采用基于优化模型的分组算法来解决地震灾害应急救援队伍的分组问题；Sampson等[10]根据参与救援人员的意向建立模型从而求解人员派遣问题；张淑文等[11]提出灾情优先、距离优先、兼顾灾情和距离3种调度策略，并采用非支配遗传算法对模型进行求解得到最优派遣策略；李亦纲等[12]基于资源优化分配模型和算法，从救灾对象的分级、救援需求分析和基于运输问题的救援力量优化调配求解方面对地震灾区救援力量优化调配模型进行较全面的研究，给出相对完整的技术思路和初步的应用，以此来提高救援效率；李怀明等[13]以整体救援效果最佳为目标，以综合救援效益为目标函数建立救援人员分组模型，虽然该模型可以得出比较合理的派遣方案，但其未考虑经济成本这一因素。虽然上述方案可以求解出灾后救援派遣方案，但其均以专业救援队为对象建立模型，不适合社会力量此类救灾群体的情况。

所谓的社会力量是指能够参与并作用于社会发展的社会组成部分，包括非政府组织、志愿者、企业等。汶川地震以后，我国越来越多的社会力量参与灾后救援行动，大大提高救援效率。如汶川地震发生之后，各类社会组织和广大志愿者火速赶往灾区参与救援[14]。在“8·8”九寨沟地震救援中社会力量也起到积极的作用[15]。社会力量在参与灾后救援中有较多优势，主要包括多渠道筹集社会资源、及时了解各类求助群体的需求和提供更加专业化的救助等[16]。但也存在一些问题，包括贸然进入灾区导致交通拥堵、救援行动缺乏协同性等。随着我国社会力量的不断发展，为健全社会力量参与灾后救援的工作机制，促进社会力量高效有序地参与灾后救援工作，2017年12月28日，民政部发布《社会力量参与一线救灾行动指南》，指出社会力量在灾后救援中应本着“量力而行、就近就便”的原则，根据灾区需求和自身擅长的领域来开展救灾工作[17]。本文针对社会力量这一救灾群体，对灾后救援派遣模型展开研究，以提高社会力量参与灾后救援的效率。

对于救援队分配模型问题，目前我国学者已经进行大量的研究，但社会力量与专业救援队有所不同，他们分散各地，面向不一，其掌握的救援技能也各不相同[18]。鉴于此，本文针对灾后社会力量救援派遣问题，综合考虑救援效益、时间成本和经济成本3个因素建立模型，并采用改进的模拟退火算法对模型进行求解，得出最优派遣策略。

1 问题描述及数学建模

社会力量组织参加灾后救援是1个复杂的社会问题，涉及到装备、技能、位置、时间、人力、财政、交通等问题，需要进行细心规划和调度，以使得救援效益最大化。

1.1 问题描述

假设有若干个受灾地区需要救助，有多个社会力量组织参与救助工作，但每个社会组织具有的救援技能不同、所在的位置不同、到达灾区的时间不同、能够接受的最大救援成本不同，根据上述情况求解最优救援派遣方案。

这是1个多参数的社会组织救灾效益最大化的求解问题，可以通过建立数学模型进行求解。

社会力量参与灾后救援模型的建立与求解示意如图1所示。本文所需求解的问题是：在得知各社会力量救援能力和灾区情况的条件下，结合实际情况调整约束条件，根据不同的灾区救援需求计算最佳派遣方案，使得综合救援效益最大。

图1 社会力量救灾派遣模型的建立与求解示意Fig.1 Schematic diagram for establishing and solving dispatch model of social forces for disaster relief

1.2 假设条件

考虑到建立多参数优化问题数学模型的复杂性，为便于研究和求解，需要进行如下合理的假设：

1)在对社会力量评估后允许其进入灾区实施救援。

2)各社会力量到达灾区的时间可以估算。

3)各社会力量前往各地的经济成本可被估算。

4)各个受灾地的受灾情况可被估计。

1.3 符号说明

由社会力量组成的救援组织(以下简称社会组织)参与灾后救援派遣模型中相关的数学量符号含义如下：

D={D1,D2,D3,…,Dm}表示灾区Di组成的集合。

M={M1,M2,M3…,Mn}表示社会组织Mj组成的集合。

P={P1,P2,P3,…,Pl}表示本次救援所需技能种类Pk组成的集合。

T={tij|i=1,2,3,…,m,j=1,2,3,…,n}表示社会组织Mj抵达灾区Di所花费的时间tij组成的集合。

F={fi|i=1,2,3,…,m}表示灾区Di的最佳救援时间fi组成的集合。

G={gij|i=1,2,3,…,m,j=1,2,3,…,n}表示不同社会组织前往不同灾区的救援经济成本gij组成的集合。

H={hj|j=1,2,3,…,n}表示社会组织Mj的救援预算成本hj组成的集合，万元。

B={bik|i=1,2,3,…,m,k=1,2,3,…,l}表示灾区Di对救援技能Pk的需求程度bik组成的集合，分为高、中、低3个等级，分别用Ⅲ，Ⅱ，Ⅰ表示。

R={rjk|j=1,2,3,…,n,k=1,2,3,…,l}表示社会组织Mj拥有救援技能Pk的等级rjk组成的集合，每种技能可分为高、中、低3个等级，分别用3，2，1表示。

S={si|i=1,2,3,…,m}表示灾区Di对社会组织的最大需求量si组成的集合。

X={xij|i=1,2,3,…,m,j=1,2,3,…n}表示社会组织Mj是否前往受灾地Di进行援助标识xij∈{0,1}组成的集合，等于1时为前往，0为不去，根据集合结果确定分配方案。

1.4 救援匹配度

每个社会组织掌握的技能各不相同，技能水平等级有高低之分。因此，根据灾区灾情，对每个社会组织救援掌握的技能等级与灾区需求的救援技能情况进行匹配度计算，帮助社会组织匹配到最合适的灾区，提高救援效率。故救援效益最大化问题转化为最佳匹配度问题。

每个社会组织的救援技能以及等级评估，按照3级原则在日常的管理中可以完成；灾害发生后，不同灾区对救援技能以及等级需求、最佳救援时间等信息可以在灾情发生后通过快速评估获得。则灾区需要的救援技能及等级与社会组织的救援技能及等级的匹配度eij计算如式(1)所示：

(1)

式中：eij为社会组织Mj对灾区Di的匹配度，值域为[0,1]，数值越接近1，表示匹配越好，越接近0，表示匹配越差。

如某灾区对救援技能需求为城市搜救能力、高空绳索能力、山地救援能力、水上救援、医疗救助能力、后勤保障能力6种救援技能，需求程度等级对应为[Ⅲ，Ⅲ，Ⅱ，Ⅱ，Ⅲ，Ⅱ]；而某组织的救援技能对应等级为[3,2,2,1,1,1]。利用式(1)计算得到该社会组织对应于灾区的技能匹配度为0.82，说明该社会组织较适合前往此灾区进行救援，再结合抵达灾区时间和经济成本考虑是否派遣至灾区。

1.5 模型及约束条件

设目标函数为救援效益最大，即所有灾区需求技能与社会组织掌握技能的总体匹配度最高，如式(2)所示：

(2)

式中：E表示综合救援效益；xij表示社会组织Mj是否前往受灾地Di进行援助。

另外需要考虑经济成本和时间因素。前往灾区的经济成本需要根据交通工具、生活成本以及其他救援成本计算总的经济成本，使之不超过社会组织的救援预算总额；时间成本可以根据社会组织所在位置到灾区的距离以及可用的交通工具进行估算，救援组织抵达灾区的时间应不超过灾区最佳救援时间。约束条件如式(3)～(7)所示：

(3)

(4)

(5)

(6)

(7)

式(3)表示经济约束；式(4)表示时间约束；式(5)表示救援技能匹配度达到0.5以上才可考虑是否将其派遣到相应灾区；式(6)表示每个救援组织只能前往1个灾区实施救援；式(7)表示派往某灾区的社会组织数量不可超过该灾区需求的最大组织数量，灾区最大救援需求量由灾区的地区系数、季节系数、事故发生时间、受灾严重程度等确定。

2 基于改进的模拟退火算法的模型求解

模拟退火算法是模拟固体冷却的原理而设计的1种优化算法，从某一较高的温度开始，随着时间的变化，温度不断地下降，直至达到与环境温度一致，此时内能减至最小[19]。算法改进如下：

1)初始解的选择

初始解为随机生成m×n维0，1矩阵，表示社会组织Mj前往灾区Di。在生成过程中，需要考虑式(7)的约束条件，即派遣到灾区的社会组织数量不得超过该灾区需求的最大组织量。

2)目标函数及约束条件

目标函数为总救援效益最大，同时，以经济成本和抵达灾区的时间作为约束条件。

3)选择新解

在初始的分配方案上随机选择1个社会组织的救援地进行更换。

4)目标函数差

计算变换前与变换后目标函数的差值ΔE，如式(8)所示：

ΔE=E′-E

(8)

式中：E′表示新解；E表示旧解。

5)Metropolis接受准则

Metropolis接受准则是1个重要性采样函数，接受准则如公式(9)所示：

(9)

式中：P表示接受新解的概率；t表示迭代次数。

在Metropolis接受准则的基础上，新方案还需满足式(3)～(7)的约束条件。如果有1个约束条件不满足，则P=0。

6)退火策略

为提高找到全局最优解的概率，使用基于牛顿冷却定律的温度衰减函数来实现。牛顿冷却定律是在考虑周围环境温度固定的条件下，计算1个热物体温度随时间变化的规律[20]，其表达式如式(10)所示：

T(t)=Tc+(T(t0)-Tc)×e-k(t-t0)

(10)

式中：t0为初始迭代次数；T(t0)为物体的初始温度，℃；T(t)为当前时刻t的物体温度，℃；Tc为周围环境温度，℃；k为衰减系数，是1个常数；t-t0为时间差，可以用迭代次数刻画，可与公式(9)保持一致。以迭代次数作为横坐标、物体温度作为纵坐标，取初始温度为100 ℃，衰减系数为0.001，绘出温度随迭代次数的变化曲线图，如图2所示。同时将指数衰减函数画在同一个坐标系下，以便于对比。

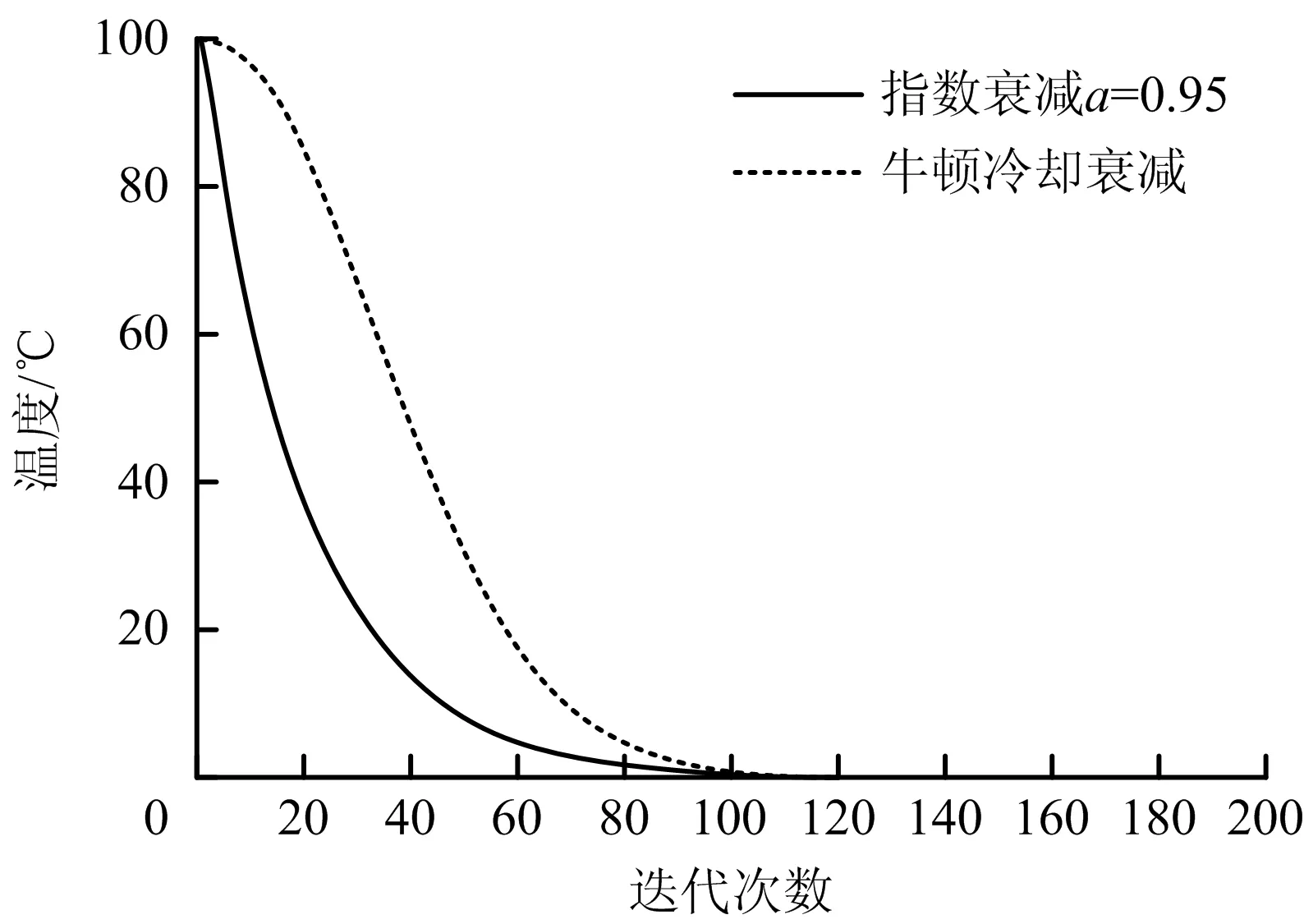
图2 不同衰减函数的温度衰减趋势Fig.2 Temperature attenuation trends of different attenuation functions

由图2可知，在相同的迭代次数下，牛顿冷却衰减函数相较于指数衰减函数温度更高，这可以在算法初期以更高的概率接受较差的解，从而提高搜索全局最优解的概率。

7)派遣方案选择

在确定社会组织情况和灾区情况之后，根据综合救援效益和时间成本、经济成本建立派遣模型，并采用改进的模拟退火算法进行求解，得到最优派遣方案。算法求解流程如图3所示。

3 实例分析

以地质灾害事件为例，利用本文所提出的模型进行计算，找出最优派遣方案。假设某地发生地质灾害，有3个受灾区，受灾程度分别为重度受灾区、中度受灾区和轻度受灾区，其中重度受灾区的人员伤亡和房屋倒塌情况比较严重，所以急需城市搜救能力和医疗救助能力较强的社会组织；轻度受灾区的人员伤亡情况较轻，对城市搜救类的组织需求不大，对后勤保障人员的需求较为迫切。针对上述情况，各灾区救援技能需求程度等级情况见表1。

现在有8个具备救援资格的社会组织请求参与本次地质灾害救援。8个社会组织的救援技能满足灾区需求的6类救援技能，技能等级分布情况见表2。

各社会组织从不同位置出发，到达灾区花费的时间见表3。3个灾区的最佳救援时间分别为5，6，7 h。并且前往救援所产生的经济成本可被估算，社会组织通往不同灾区的经济成本见表4。8个组织的救援预算成本分别为14，13，13，11，13，11，13，15万元。

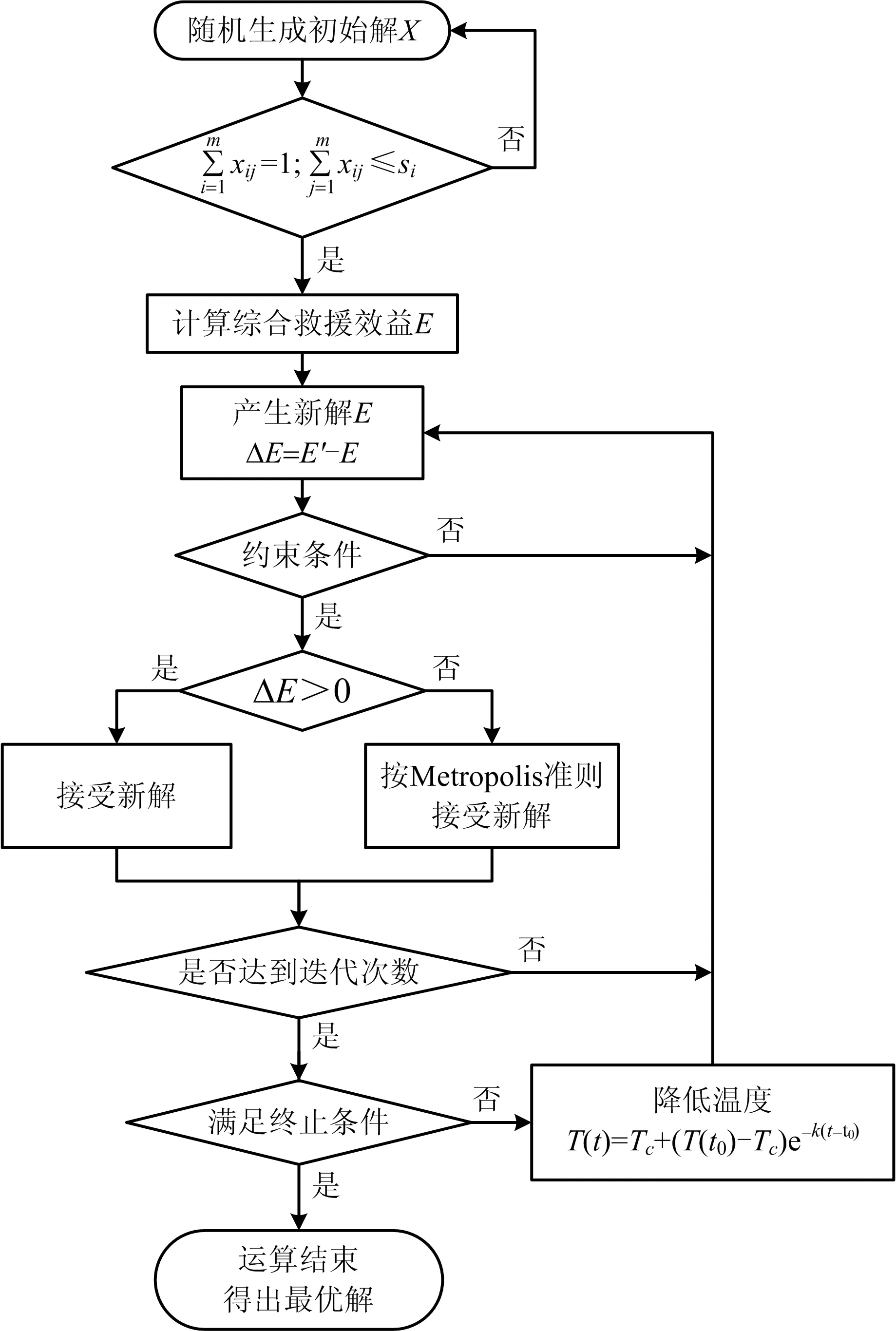
图3 基于改进模拟退火算法的模型求解流程Fig.3 Flow chart of model solving based on improved simulated annealing algorithm

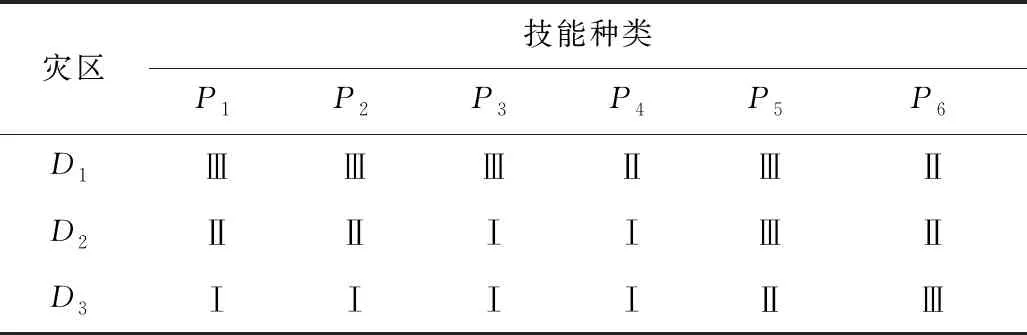
表1 各灾区救援技能需求程度的等级情况Table 1 Grades of requirement degree for rescue skills by each disaster area

根据式(1)，计算社会组织对于灾区的救援技能匹配度，计算结果见表5。匹配度数值范围为[0,1]，数值越接近于1，表示救援技能越匹配。

通过改进的模拟退火算法得出最佳派遣方案，根据是否考虑时间约束和经济约束得出4组派遣方案，见表6～9。其中，方案1考虑时间约束和经济约束；方案2不考虑时间约束、经济约束；方案3考虑时间约束、不考虑经济约束；方案4不考虑时间约束、考虑经济约束。

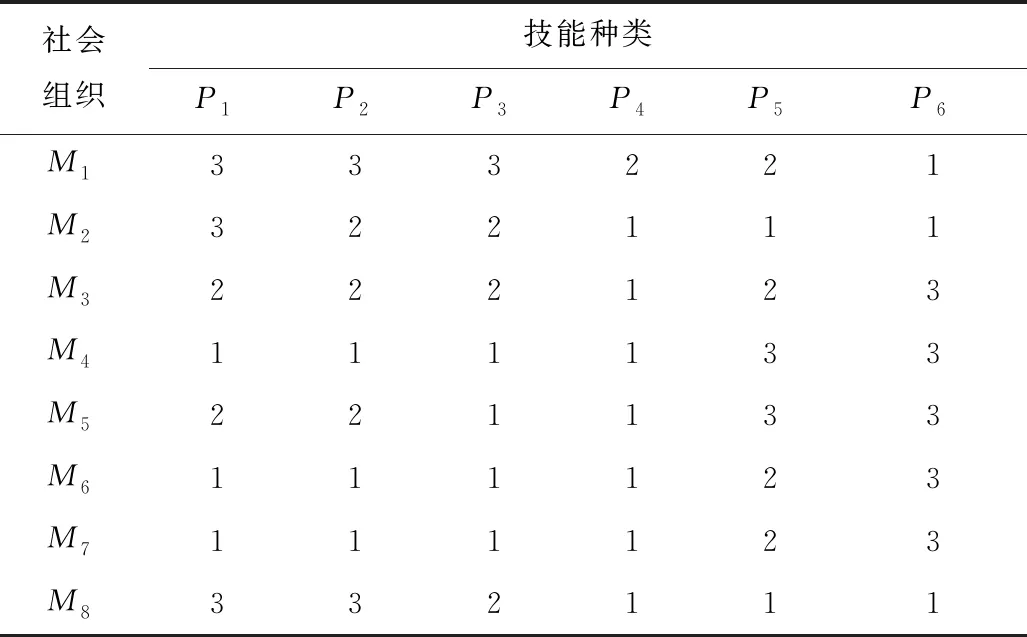
表2 社会组织救援技能等级Table 2 Rescue skills grades of social organizations

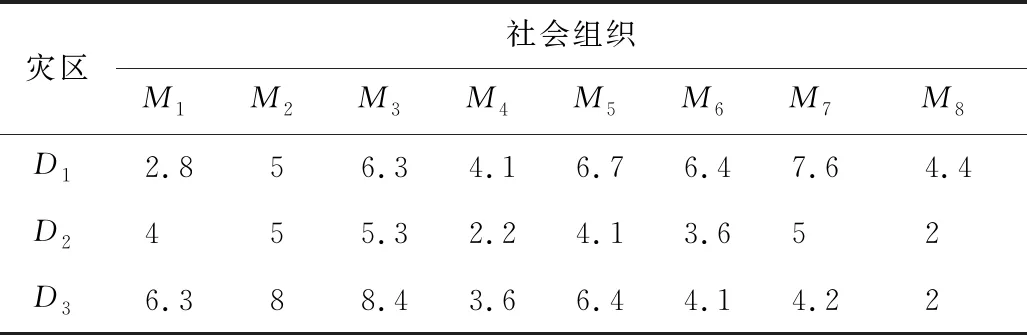
表3 社会组织抵达不同灾区花费的时间Table 3 Time for social organizations to arrive at different disaster areas h

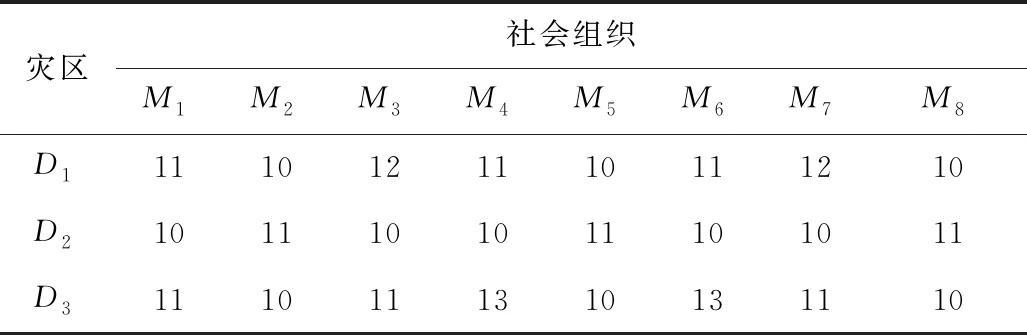
表4 社会组织通往不同灾区的经济成本Table 4 Economic costs of social organizations to different disaster areas 万元

表5 救援技能匹配度Table 5 Matching degree of rescue skills

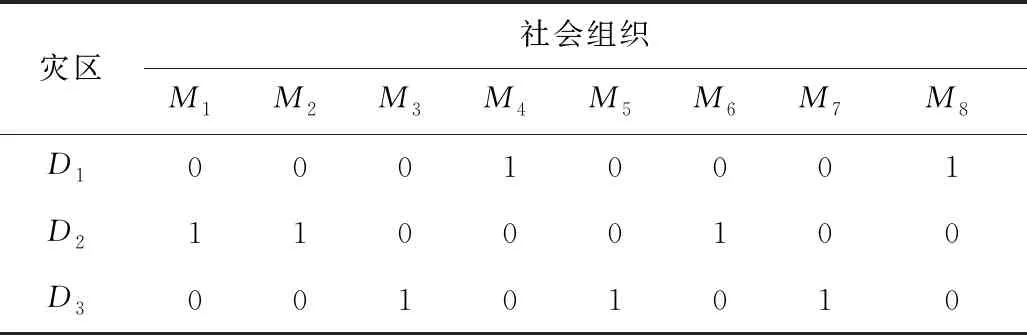
表6 模拟退火算法对模型的求解结果(方案1)Table 6 Solving results of simulated annealing algorithm to model (scheme 1)

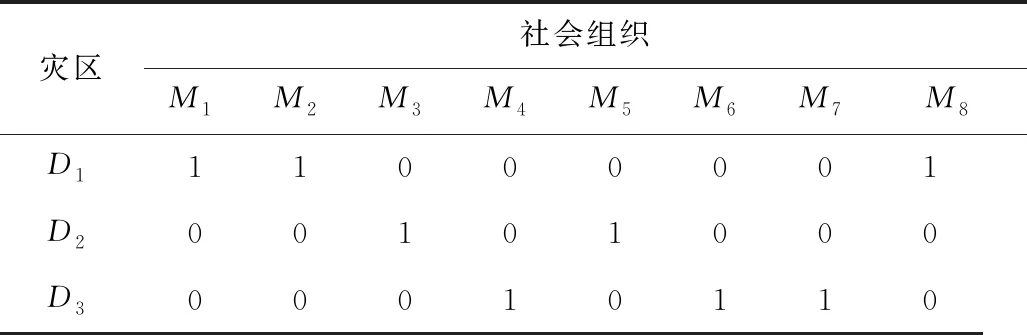
表7 模拟退火算法对模型的求解结果(方案2)Table 7 Solving results of simulated annealing algorithm to model (scheme 2)

表8 模拟退火算法对模型的求解结果(方案3)Table 8 Solving results of simulated annealing algorithm to model (scheme 3)

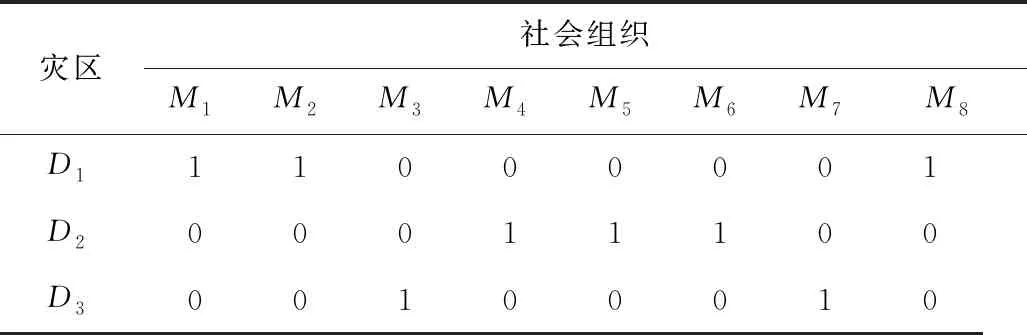
表9 模拟退火算法对模型的求解结果(方案4)Table 9 Solving results of simulated annealing algorithm to model (scheme 4)

通过计算求得4个方案的总救援效益、总花费时间和总经济成本见表10。

从结果中可以看出，考虑时间约束和不考虑时间约束的派遣结果均满足灾区最大救援需求量此约束条件。从救援效益和时间上来看，方案2的总救援效益高于方案1的总救援效益，且其总花费的时间较低，符合时间约束条件；从经济成本上看，加入经济成本约束后的派遣结果其花费更低，如方案4与方案3相比，其经济成本相差4万元。因此，不同的约束条件可以得出不同的派遣方案，可根据实际情况对时间约束进行调整，以得到最佳派遣策略。

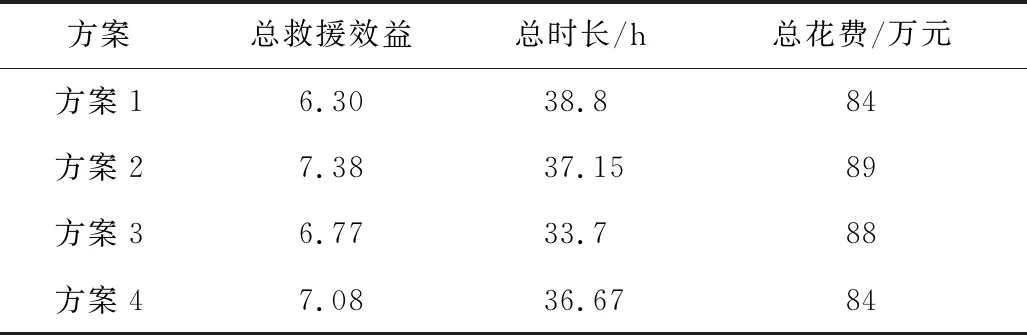
表10 总救援效益、花费时间和经济成本计算结果Table 10 Calculation results of total rescue benefits,time spent and economic costs

4 结论

1)根据“量力而行、就近就便”等原则，应综合考虑救援效益、时间成本、经济成本3个因素建立灾后救援派遣模型。

2)采用模拟退火算法对模型进行求解，根据模型改进Metropolis接受准则，并用牛顿冷却定律作为温度衰减函数。最后通过算例结果来证实该社会组织救援派遣模型的可行性，为社会组织参与灾后救援提供决策支持。

3)根据实际情况调整约束条件，可以得出符合灾区救援需求情况的派遣方案。

4)在救援派遣模型建立时，社会组织成员人数未确定，因此模型与实际情况存在一定的误差，在实际应用时需对个别参数进行修正。