椭圆曲线y2=x3+9x-26的整数点

谢甜甜, 杨 海, 罗永亮

(西安工程大学 理学院, 陕西 西安 710048)

椭圆曲线是代数几何中重要的曲线之一,至今已有100多年的历史,众多学者对找椭圆曲线整数点的问题有着浓厚的兴趣,在此期间也产生了大量的研究成果[1-5],这些成果也被广泛地应用于密码学中.但由于椭圆曲线求解的复杂性与参数的多变性,至今也没有一个系统的求解方式.目前,对于椭圆曲线

y2=(x+a)(x2-ax+b)

(1)

整数点的相关问题,主要集中在a=±2,±6,7上, 具体结果如下.

1) 当a=±2时:杜先存等[6]利用Legendre符号、同余式、Pell方程的解的性质等初等方法证明了a=-2,b=p,其中p=36s2-5时,椭圆曲线(1)仅有整数点为(-2,0);崔保军[7]利用初等方法证明了当a=-2,b=18时,椭圆曲线(1)仅有整数点(x,y)=(2,0),(106,±1 092);崔保军[8]运用同余、递归序列等初等方法证明了当a=-2,b=139时,椭圆曲线(1)仅有整数点(x,y)=(2,0),(14,±66),(284 594±151 823 364);管训贵[9]证明了当a=-2,b=m,其中m=4p-8=q+1或m=2p-8=q+1且p≡1(mod 8)(p,q为素数)时,椭圆曲线(1)上的所有整数点(x,y);赵建红[10]证明了当a=-2,b=15时,椭圆曲线(1)无正整数点;杜先存等[11]利用同余式、Legendre符号、Pell方程的解的性质等初等方法给出了当a=2,b=27时,椭圆曲线(1)无正整数点.

2) 当a=6时:过静[12]运用初等数论方法给出了当a=6,b=15时,椭圆曲线(1)无正整数点;赵建红等[13]利用唯一分解定理、同余的性质、Legendre符号的性质、奇偶数的性质、Pell方程的解的性质等初等方法证明了当a=6,b=19时,椭圆曲线(1)无正整数点;万飞等[14]证明了当a=-6,b=23时,椭圆曲线(1)无正整数点.

3) 当a=7时:董鑫等[15]利用二次剩余等初等数论方法与技巧证明了当a=7,b=19时,椭圆曲线(1)仅有整数点(x,y)=(-7,0),(-3,±14),(2,±9),(6,±13),(5 143 326,±11 664 498 677).

到目前为止,当a=2,b≡5(mod 8)为素数时,椭圆曲线(1)无相关结论.本论文将证明当a=2,b=13时,椭圆曲线(1)整数点的情况.

1 相关引理

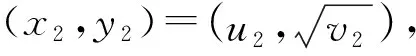
2 定理及定理的证明

定理椭圆曲线

y2=x3+9x-26

(2)

有整数点(x,y)=(2,0),(5,±12),(9,±28),(86,±798).

证明 设(x,y)是式(2)的解,由式(2)可得

y2=(x-2)(x2+2x+13).

(3)

由于x3+2x+13=(x+1)2+12>0,则从式(3)可知x≥2.当x=2时椭圆曲线(2)有整数点(x,y)=(2,0).因此以下只需考虑x>2时椭圆曲线(2)有解的情况.

因为gcd(x-2,x2+2x+13)=(x-2,21)=1,3,7,21.所以将式(3)分解成下面4种情形进行讨论.

情形Ⅰ:x-2=u2,x2+2x+13=v2,y=±uv,gcd(u,v)=1,u,v∈N+.

情形Ⅱ:x-2=3u2,x2+2x+13=3v2,y=±3uv,gcd(u,v)=1,u,v∈N+.

情形Ⅲ:x-2=7u2,x2+2x+13=7v2,y=±7uv,gcd(u,v)=1,u,v∈N+.

情形Ⅳ:x-2=21u2,x2+2x+13=21v2,y=±21uv,gcd(u,v)=1,u,v∈N+.

情形Ⅰ由第2个式子可得(x+1)2+12=v2,则有(v+x+1)(v-x-1)=12,得到仅有当v=4,x=1时,满足u,v∈N+的条件, 将x=1代入第1个式子中可得-1=u2,显然不成立,故该情形下椭圆曲线(2)无整数解.

情形Ⅱ由于x=3u2+2, 将其代入x2+2x+13=3v2中并整理可以得到

v2-3(u2+1)2=4,

(4)

从式(4)可知方程

X2-3Y2=4

(5)

有解

(X,Y)=(v,u2+1).

(6)

由于方程

s2-3t2=4,

(7)

的基本解为(s,t)=(4,2),由式(5)与式(7)知,如果(X,Y)是式(5)的解,则式(7)必有解为(s,t)=(X,Y),则根据引理1可知,式(4)的全部正整数解满足

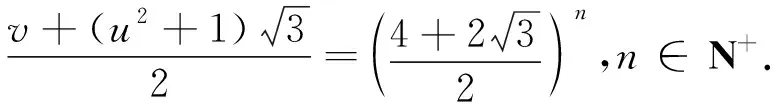
(8)

当n=1,u=1,v=4时式(8)成立,即从式(8)可知式(5)仅有1组解(X,Y)=(4,2).当u=1,v=4时,由x=3u2+2=5,y=±3uv=±12,可得椭圆曲线(2)有整数点(x,y)=(5,±12).

情形Ⅲ因为x=7u2+2,将其代入x2+2x+13=7v2中并整理可得

4u4+3(u2+1)2=v2.

(9)

当u=1,v=4时式(9)有解,由x=7u2+2=9,y=±7uv=±28可得椭圆曲线(2)有整数点(x,y)=(9,±28).

情形Ⅳ因为x=21u2+2,将其代入x2+2x+13=21v2中并整理可得

3(u2+1)2+18u4=v2.

(10)

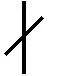
u=2w,w∈Z+,

(11)

此时x=21u2+2为x=84w2+2,将其代入x2+2x+13=21v2中并整理可得

(12w2+1)2+192w4=v2.

(12)

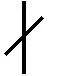
又因gcd(12w2+1,192w4)=gcd(12w2+1,26×3w4)=gcd(12w2+1,26×3)=1,即gcd(v+12w2+1,v-12w2-1)=2.因为192=26×3,则可以将式(12)分解为

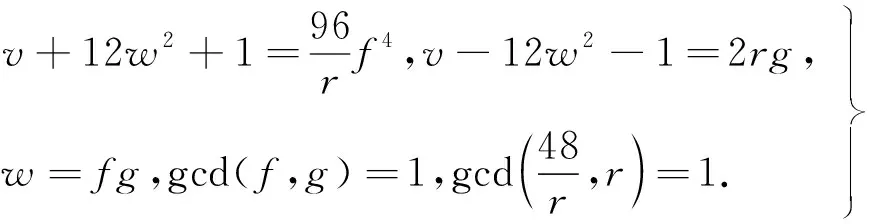
(13)

式中r=1,3,16,48.

由式(13)的前2式得

(14)

对式(14)两边分别取模3可得

(15)

对(14)式两边分别取模4可得

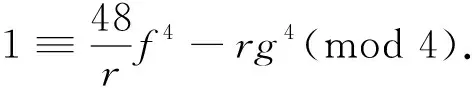
(16)

当r=1时,式(15)为

1≡-g4(mod 3).

(17)

当r=3时,式(14)为

12w2+1=16f4-3g4,

(18)

将式(18)整理可得

28f4-3(g2+2f2)2=1,

(19)

令s=2f2,t=g2+2f2,则式(19)为

7s2-3t2=1.

(20)

设式(20)有正整数解(s,t),而Pell方程(20)的基本解为(2,3),则式(20)的全部解可以被表示为

即式(19)的全部解表示为

(21)

当f=1,g=1时,式(21)成立,即从式(21)可知式(20)仅有一组解,由式(11)、式(13)可知w=1,u=2,v=19,故此时椭圆方程(2)有整数点(x,y)=(86,±798).

当r=16时,式(16)为

1≡3f4(mod 4).

(22)

由于f2≡1(mod 4),则f4≡1(mod 4),即3f4≡3(mod 4),故1≡3(mod 4),因此式(22)不成立,即当r=16时,式(13)不成立,故情形Ⅳ不成立.

当r=48时,式(14)为

12w2+1=f4-48g4,

(23)

将式(23)配方可得

(f2-6g2)2-84g4=1,

(24)

令u=f2-6g2,v=2g2,则式(24)为

u2-21v2=1,

(25)

若式(25)有正整数解(u,v),而Pell方程(25)的基本解为(55,12),则式(25)的全部正整数解可表示为

(26)

由此可知,式(24)的全部正整数解可表示为

(27)

令sn=f2-6g2,rn=2g2,n∈Z+,可以验证式(28)成立,

rn+2=110rn+1-rn;r0=0,r1=12.

(28)

对递归序列(28)取模11,得到周期为2的剩余类0,1,0,1,…,并且在n≡1(mod 2)时,有rn≡1(mod 12);n≡0(mod 2)时,有rn≡0(mod 12).由于rn=2g2,则rn为偶数,故当n≡0(mod 2)时,式(27)才能成立.

解得f2-6g2=6 049,g2=660,显然无正整数解,即当r=48时,式(13)不成立,故情形Ⅳ不成立.

综上定理得证.

3 结 论

本文得到了当a=2,b=13时,椭圆曲线y2=(x+a)(x2-ax+b)仅有整数点(x,y)=(2,0),(5,±12),(9,±28),(86,±798).研究结果对于研究当a,b∈Z时椭圆曲线y2=(x+a)(x2-ax+b)的求解有一定的借鉴作用.