广义渐近伪非扩张半群不动点Cesro平均黏滞迭代逼近

张树义, 张芯语

(渤海大学 数理学院, 辽宁 锦州 121013)

式中:{αn}、{βn}是[0,1]中的实数列;f:H→H是压缩映象;α∈(0,1)是强正有界线性算子;I是恒等映象;T={T(t):t∈R+}是渐近非扩张半群类(广义渐近伪非扩张半群,广义渐近非扩张半群,渐近非扩张半群)并在一定条件下,在Hilbert空间中建立了广义渐近伪非扩张半群不动点的Cesro平均黏滞迭代序列式(1)的强收敛性定理,从而推广和改进了相关文献中的结果.

1 预备知识

定义1 设C是Banach空间E的非空闭凸子集.

1) 映象f:C→C称为压缩的,若存在α(0<α<1),对∀x,y∈C,有‖f(x)-f(y)‖≤α‖x-y‖.

定义3 设C是Banach空间E的非空闭凸子集,R+表示非负实数集.一族映象T={T(t):t∈R+}:C→C被称为渐近非扩张半群,如果满足下列条件:

1)T(0)x=x,∀x∈C;

2)T(s+t)x=T(s)T(t)x,∀x∈C和∀s,t∈R+;

3) ∀x∈C,映象tT(t)x对t∈R+是连续的;

‖(T(t))nx-(T(t))ny‖≤(1+hn)‖x-y‖,∀t≥0.

在上面定义中如果条件4)被下列条件代替:

‖(T(t))nx-(T(t))ny‖≤(1+hn)‖x-y‖+ξn,∀t≥0,

则称T为广义渐近非扩张半群.

在上面定义中如果F(T)非空,条件4)被下列条件代替:

‖(T(t))nx-(T(t))ny‖≤(1+hn)‖x-y‖+ξn,∀t≥0,

则称T为广义渐近伪非扩张半群,其中F(T)表示半群T的公共不动点集,即

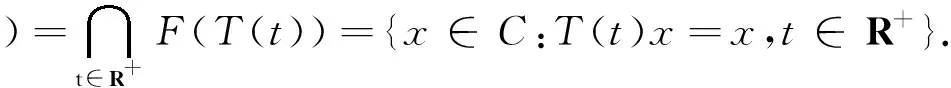
注1 易知具有不动点的渐近非扩张半群,广义渐近非扩张半群一定是广义渐近伪非扩张半群,但反之一般不成立.

定义4 一非线性半群T={T(t):t∈R+}:C→C称为Lipschitz的,若存在L≥1,使得∀x,y∈C,有‖(T(t))x-(T(t))y‖≤L‖x-y‖.

注2 易知T={T(t):t∈R+}:C→C是渐近非扩张半群,则T一定是Lipschitz的,其中L=1+h1.

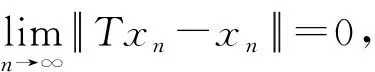
引理2 设H是实Hilbert空间,则对∀x,y∈H,有‖x+y‖2≤‖x‖2+2〈y,x+y〉.

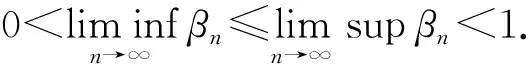
2 主要结果

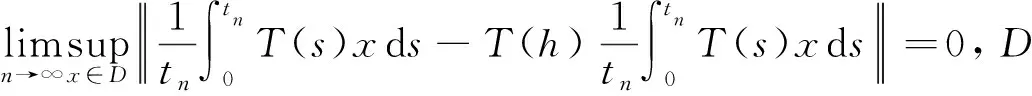
〈(γf-A)q,z-q〉≤0, ∀z∈F(T).

(2)

下面证明{xn}有界,∀p∈F(T),由式(1),∀n>N,有

因此{xn}有界,从而

也有界.由式(1)

下面证明‖xn-T(t)xn‖→0(n→∞).设

其中p∈F(T),则D是C的非空有界闭凸子集{xn}⊂D,并且T是D上广义渐近伪非扩张半群,于是

据此有

又因{xn}有界,所以存在子列{xnj}⊂{xn},使得{xnj}弱收敛于q.由引理1知,对每一t>0,q=T(t)q,故q∈F(T).

容易证明满足变分不等式(2)的解是唯一的.最后证明xn→q(n→∞),由式(1)和引理2,有

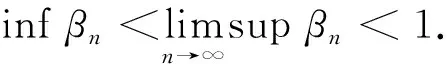
式中D是C的有界子集,则式(1)定义的广义渐近非扩张半群Cesro平均黏滞迭代序列{xn}强收敛于广义渐近非扩张半群T的公共不动点q∈F(T),且q是下列变分不等式的解:

〈(γf-A)q,z-q〉≤0, ∀z∈F(T).

从而

注意到

在定理2中取ξn≡0,便得渐近非扩张半群Cesro平均黏滞迭代序列的强收敛定理.

3 结 论

广义渐近伪非扩张半群是一类比较广泛的非线性映象, 它以非扩张半群、 渐近非扩张半群和渐近伪非扩张半群为特例. 而广义渐近伪非扩张半群是渐近伪非扩张半群的推广, 因此研究其迭代逼近问题是非常有意义的. 本文引入了广义渐近伪非扩张半群Cesro平均黏滞迭代算法, 在一定条件下,在Hilbert空间建立了广义渐近伪非扩张半群不动点Cesro平均黏滞迭代序列的强收敛性定理, 推广和改进了一些文献中的相关结果.