内啮合弧面凸轮机构压力角的计算方法

2021-03-10

包装与食品机械 2021年1期

（陕西科技大学机电工程学院，西安 710021）

0 引言

弧面凸轮机构由于其良好的工作特性，在高速重载的分度机构中广泛应用，近年来，尤其是在各类食品包装机械中受到越来越多的重视［1-4］。国内外学者对其运动［5-7］、动力学特性和设计制造等方面进行了广泛的研究［8-10］。这些研究成果推动了弧面凸轮机构的发展，但均针对外啮合这一传动方式，本文提出内啮合弧面凸轮机构这一新的传动形式。

虽然内啮合和外啮合空间曲面啮合理论相同，针对外啮合情况下机构的建模［11］、压力角［12］、凸轮曲线设计等多个方面已取得了一些研究成果［13］，但内啮合时上述这些方面均会发生变化。由于压力角是影响机构运动特性和受力情况的重要参数，本文以多年来课题组对弧面凸轮机构的研究为基础，以内啮合弧面凸轮机构为研究对象，利用空间坐标系回转张量变换的方法，建立了内啮合时压力角的计算公式，并分析了压力角的影响因素，完善了弧面凸轮机构的设计理论。

1 凸轮轮廓曲面方程

内啮合弧面凸轮机构由弧面凸轮、从动盘和向内辐射的滚子组成。相比于外啮合形式，其结构更加紧凑，分度数更多。

1.1 建立坐标系

建立空间坐标系，如图1所示。4个坐标系分别为：固定坐标系o-xyz：z轴与从动盘回转轴线重合，x轴是凸轮回转轴与从动盘回转轴的公垂线，x轴与z轴的交点为原点o，y轴与凸轮回转轴y1平行。凸轮坐标系o1-x1y1z1与凸轮固结，y1轴为凸轮的回转轴，原点o1为凸轮曲面的基准点。从动件坐标系o2-x2y2z2与从动盘固结，原点o2与o重合，z2为从动盘回转轴，x2轴与从动盘回转臂中心线o2o3重合。滚子坐标系o3-x3y3z3与从动件固结，原点为滚子的基准点o3，x3y3z3分别与x2y2z2平行。

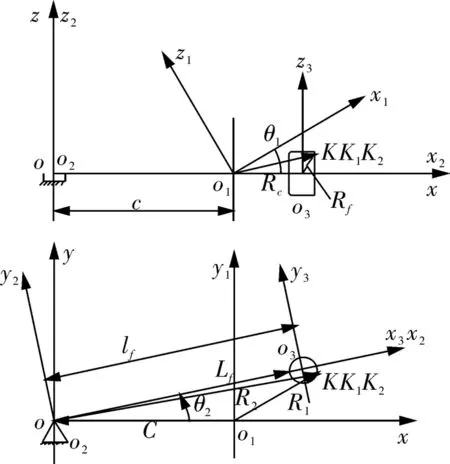
图1 内啮合弧面凸轮机构矢量关系图Fig.1 Vector diagram of the internal meshing globoidal cam mechanism

某一瞬时，凸轮曲面上的K1点与从动盘滚子曲面上的K2点啮合于固定坐标系上的K点，各矢量关系如图2所示。凸轮轮廓曲面的几何形状矢量函数为，滚子的几何形状矢量函数为，滚子中心o3在从动件坐标系中的位置矢量为，其中 i=［1，0，0］T，lf为从动盘回转半径。在固定坐标系中，R1、R2分别是啮合点K相对于o1、o2点的位置矢量，C为中心距矢量，分别表示为：，三者之间的关系为：

1.2 凸轮轮廓曲面方程

利用回转变换张量［14］，将 Rc、Rf转换为固定坐标系中的矢量R1、R2，即可得到凸轮曲面矢量方程：

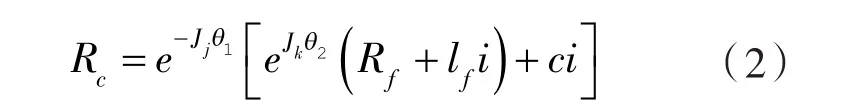
式中 θ1——凸轮在凸轮坐标系中的角位移；

θ2——从动盘在从动件坐标系中的角位移。

根据空间曲面啮合条件［14］：

式中 n ——两曲面在K点处的公共法矢量，

V21——K点在公切面上的相对滑动速度；

由此可求得内啮合弧面凸轮轮廓曲面方程组：

圆柱滚子坐标参数如图2所示。δf表示母线方向参数，这里指滚子宽度的一半。βf表示圆周方向参数。rf表示滚子半径。

图2 圆柱滚子坐标参数图Fig.2 Coordinate parameter diagram of cylindrical roller

在滚子坐标系中，滚子曲面矢量Rf和法向单位矢量nf分别表示如下。

结果显示，βf与滚子半径rf无关。

因此，圆柱滚子内啮合弧面凸轮轮廓曲面矢量函数为：

2 压力角的计算

2.1 压力角的计算公式

内啮合弧面凸轮机构的压力角α，如图3所示，是指从动盘滚子曲面上接触点K2处所受的驱动力方向（-nf）与该点速度方向（tf）之间所夹的锐角。把从动曲面在接触点处法线方向的反方向作为凸轮驱动力的方向，接触点处的法线方向为nf，它与K2点处滚子矢量函数Rf的方向一致；忽略摩擦力，取滚子中心o3的速度方向作为接触点处的速度方向tf，可得内啮合弧面凸轮机构的压力角α为：

图3 压力角Fig.3 Pressure angle

2.2 凸轮几何尺寸与压力角的关系

凸轮基圆半径与压力角的关系见下式，凸轮节圆轮廓各点的压力角近似为：

式中 V2——从动件运动规律的无因次化速度；

R1——凸轮基圆半径，mm；

φ2——从动盘的分度角；

φ1——凸轮动程角。

凸轮基圆半径与中心距的关系如图4所示。

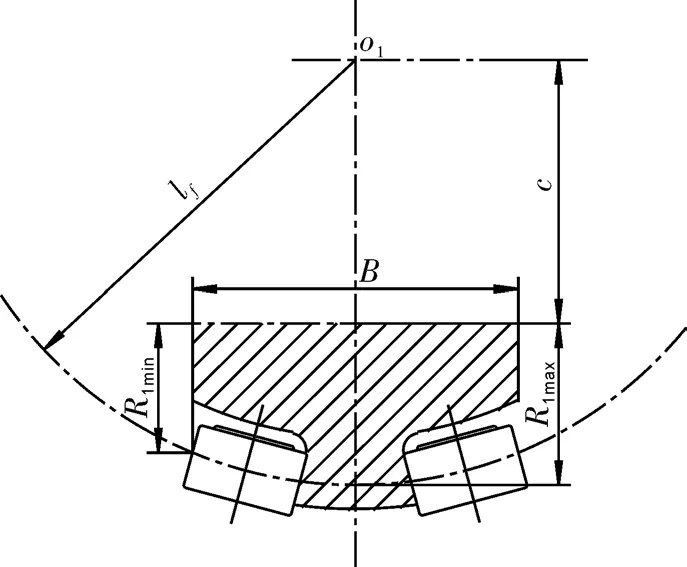
图4 凸轮基圆半径的确定Fig.4 Base circle radius of cam

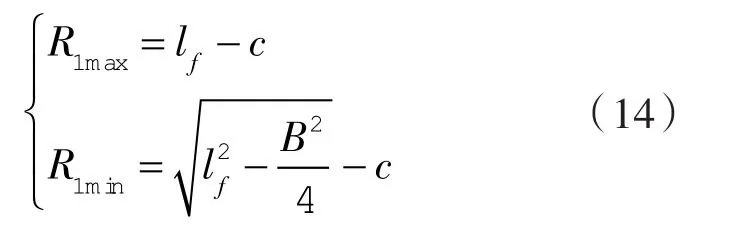
式中 B ——凸轮宽度，mm。

3 压力角的影响因素

从式（12）和式（13）可以看出，凸轮机构压力角与中心距c、从动盘回转半径lf、滚子宽度的一半δf、从动盘角位移 θ2、凸轮基圆半径及凸轮和从动件的运动规律有关。以某一包装机械分度盘的凸轮分割器为例，凸轮匀速转动，从动盘作正弦加速度运动，分度数24，中心距100 mm，从动盘回转半径145 mm，滚子宽度11 mm，分度角7.5°，凸轮动程角42°，上述各参数代入式（12）和式（13），从动件运动规律以无因次化形式代入。

机构压力角变化趋势如图5所示。

图5 不同时刻机构的压力角Fig.5 Pressure angle of the mechanism at different time

任意时刻，从动件上的机构压力角随凸轮转角的变化而变化，呈对称分布，最大压力角出现在T=0.5时刻，两种计算方法的最大值分别为50.38和50.96，结果相近。

下面分析上述各因素对压力角的影响［14-15］。滚子相关尺寸的选择参照凸轮随动器尺寸。

滚子宽度分别为 8、9、11、12、14 时，机构压力角的最大值分别为 50.26、50.3、50.38、50.41、50.49，如图6所示，随滚子宽度增大，压力角略有增加，影响甚小。

图6 滚子宽度对压力角的影响Fig.6 Influence of roller width on pressure angle

当取滚子宽度11 mm，图7显示了滚子宽度不变，不同啮合点时压力角的变化规律。相对于凸轮转角，压力角仍呈对称分布，最大压力角仍发生在T=0.5时刻，沿滚子母线方向看，越靠近滚子顶端，压力角越小，越靠近滚子根部，压力角越大，这是由于在实际啮合过程中，接触线在圆柱滚子表面是一曲线，各啮合点处δf不同，压力角也不同。

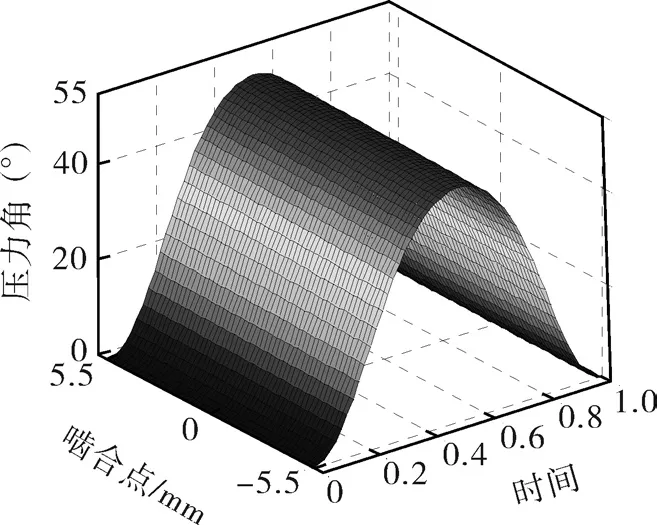
图7 啮合点对压力角的影响Fig.7 Influence of meshing point on pressure angle

当分度数不变，滚子直径df分别选取13、16、19、22时，同时增大从动盘节圆半径，节圆半径对压力角的影响如图8所示。随滚子半径增加，压力角最大值分别为：45.79、48.42、50.39、51.91，即从动盘回转半径越大，压力角越大；从上述分析可以看出，随机构尺寸的增加，压力角略有增大，机构尺寸越小，影响越明显。

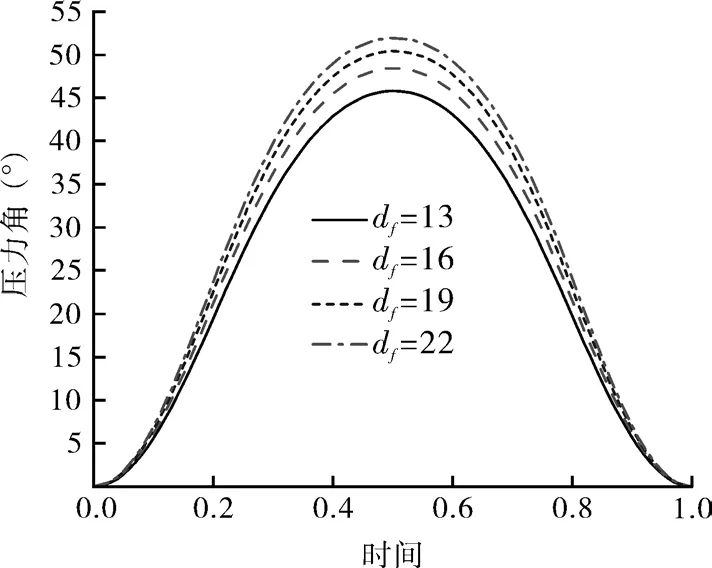
图8 节圆半径对压力角的影响Fig.8 Influence of pitch radius on pressure angle

中心距与机构压力角的关系，单由式（12）可得，中心距越大，压力角越小，如图9（a）实线所示。但由式（13）和式（14）可得，中心距越大，基圆半径越小，压力角越大，如图9（a）虚线所示。综合（12）～（14）式，可以看出，中心距的变化所引起凸轮基圆半径的变化对压力角的影响，远大于中心距变化本身对压力角的影响，因此，中心距越小，基圆半径越大，压力角越小。将原机构中中心距100分别减小为95和90，压力角的最大值分别减小到47.77和44.88，结果如图9（b）所示。

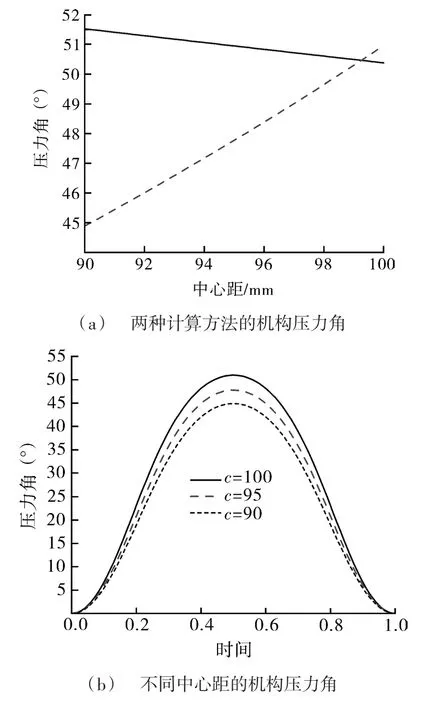
图9 中心距对压力角的影响Fig.9 Influence of center distance on pressure angle

由压力角的计算公式可以看出，从动件运动规律的选择会影响压力角的大小，图10所示为选择5种不同运动规律时机构压力角的大小。5种运动规律按照压力角的最大值从大到小分别为：正弦加速度运动规律50.38，5次多项式运动规律48.55，修正正弦运动规律46.74，余弦加速度运动规律43.49，修正等速运动规律38.71。由此可以看出，从动件运动规律对压力角的影响明显。