基于响应面分析法的粮食搬运RGV抓手优化设计

（河南工业大学 机电工程学院，郑州 450001）

0 引言

成品粮的仓储是关系到国计民生的重要问题。近年来，成品粮自动化立体仓库逐渐成为主流的发展趋势。夹抱式粮食搬运RGV（Rail Guided Vehicle，有轨引导小车）是成品粮自动化立体仓库中的关键主机设备如图1所示，主要完成粮食的存取与搬运，在粮食仓储设备中占有非常重要的地位。

图1 夹抱式粮食搬运RGVFig.1 Clamping grain handling RGV

取货抓手是夹抱式粮食搬运RGV的重要装置，在工作过程中，承受着较大和交变的工作载荷，极易发生结构变形和疲劳破坏，而且其尺寸受到车体实际结构空间的限制，给设计工作带来很大麻烦。如果抓手的结构及尺寸设计不合理，则会严重影响抓手的结构强度和刚度，降低存取货物的效率［1-2］。

针对粮食搬运RGV抓手的结构设计问题，本文以CLJ2106型夹抱式粮食搬运RGV为对象，利用ANSYS软件，并结合响应面分析法，对RGV抓手进行尺寸优化设计，使抓手在满足强度和刚度要求的同时，结构更加轻量化。

ANSYS/Workbench具有强大的优化设计功能，其中的优化工具Design Exploration，不仅可以基于常见的CAD建模平台对三维模型进行参数化定义，而且可以进行实验设计和响应面分析，从而实现对设计参数的准确把握［3-4］。

响应面分析法是通过确定性的试验来拟合一个响应面，进而模拟真实的极限状态，它是一种近似拟合方法，Workbench软件中的Response Surface分析工具就采用了这种分析方法［5］。

将参数化建模方法和响应面分析方法应用于抓手尺寸优化设计中，能够保证抓手结构的力学性能，显著缩短设计周期，降低设计成本，对提高粮食搬运RGV作业效率具有重要的意义。

1 粮食搬运RGV抓手结构与工况分析

在成品粮自动化立体仓库中，粮袋通常是以托盘形式承载并码垛成型，RGV主要依靠伸缩臂及其抓手完成托盘货物的存取。本文RGV抓手装置的主要常规尺寸为：长162.5 mm、宽25 mm、厚10 mm，整个抓手采用45钢，材料的性能参数如表1所示。

表1 45钢的性能参数Table 1 Performance parameters of 45 steel

RGV取货时，连接在车体上的抓手臂可以进行伸缩往复运动，其内侧的驱动电机轴旋转，带动抓手旋转到与抓手臂垂直的位置，此时，为了便于定位，抓手的两侧正好嵌入到抓手臂部的卡槽中，抓手在抓手臂的支撑和带动作用下，将货物拉至车体上。其工作原理如图2所示。

图2 抓手工作原理图Fig.2 Working principle diagram of gripper

取货时，RGV抓手主要承受的载荷有：货物施加给抓手的正压力F1（均布载荷）、抓手臂部的卡槽对抓手的支撑力F2和F3，抓手承受的载荷如表2所示。

表2 抓手承受的载荷Table 2 Load of gripper

抓手的载荷分布情况如图3所示。

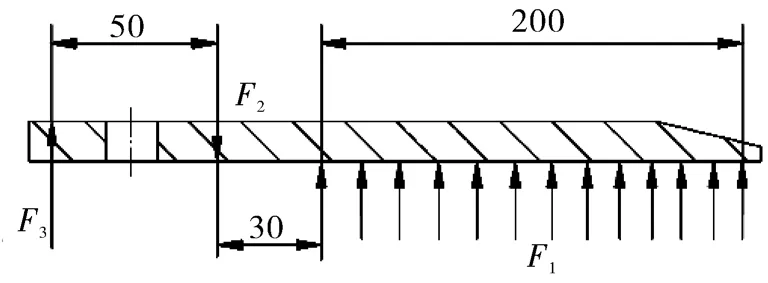
图3 抓手的载荷分布情况Fig.3 Load distribution of gripper

2 基于ANSYS的零件尺寸优化设计方法

基于ANSYS/Workbench进行零件尺寸优化设计的具体步骤为：

（1）参数化建模：在三维建模软件中建立优化对象的参数化模型，使该模型的设计参数可以被Workbench识别。

（2）静力学分析与求解：采用Workbench中的Static Structural模块对参数化模型进行静力学分析，建立静力学分析模型，定义工程材料数据、划分网格并添加载荷和约束。借助ANSYS软件强大的分析求解功能，依据强度理论分析零件的失效和变形情况，求解出力学模型的最大等效应力、最大变形、安全系数等各个性能参数。

（3）确定约束条件和优化目标：求解完成之后根据设计需求设置需要优化的输出参数，在Workbench中调用Design Exploration中的优化模块，采用响应面优化分析方法，设置所要优化的输入参数及变化范围，设置实验类型，更新和计算设计点，创建响应面等［6］。

（4）参数优化评估：迭代计算完成后，Workbench软件重新更新了设计点，并在DM中重建几何尺寸，通过静力学分析求解，判断目标函数在该设计点是否可以取得最小值，若取得最小值，则表示已经到达最优解，迭代完成；否则将继续循环迭代，直至到达最优解为止。

零件尺寸优化设计流程如图4所示。

图4 零件尺寸优化设计流程图Fig.4 Flow chart of parts size optimization design

3 粮食搬运RGV抓手尺寸优化设计

3.1 参数化模型的建立

采用SolidWorks对RGV抓手结构进行三维建模，由于Workbench软件里面不能分辨设计变量，所以要实现模型的参数化设计，首要任务是将SolidWorks与Workbench进行软件间的无缝连接，使参数可以被Workbench软件识别，其次在实际建模时，将所要绘制的零件草图中设计变量的名称前加上“DS_”的前缀，而当一些特征尺寸为设计变量时，需要先添加一个全局变量，在变量名称前同样加上“DS_”的前缀，并给定初始值，以确保模型导入后会被Workbench软件识别［7］。在Solidworks中建立的抓手参数化模型，如图5所示。

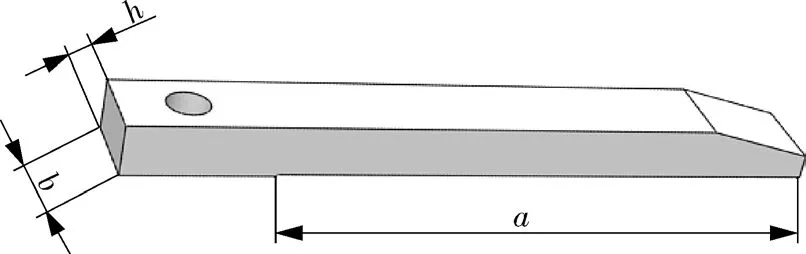
图5 RGV抓手参数化模型Fig.5 Parametric model of RGV gripper

3.2 静力学分析与求解

在Workbench中，建立RGV抓手的静力学分析模型，定义工程材料数据、划分网格并添加载荷和约束，除此之外，分别设置最大等效应力、最大变形、安全系数等作为RGV抓手静力学分析的性能参数。静力学分析过程如图6所示。

图6 静力学分析过程Fig.6 Statics analysis process

3.3 设计变量与目标函数的确定

对RGV抓手进行尺寸优化设计时，以其产生最小变形为优化目标，通过改变抓手的尺寸参数，添加固定的约束和压力载荷，分析其产生的应力应变情况，从而对其结构尺寸进行改进优化。

首先在Solidworks中将需要优化的抓手尺寸变量进行参数化处理，然后在Workbench中分别设置抓手设计参数的范围［8］，如表3所示。其中P1、P2、P3分别为抓手与货物接触面的长度a、宽度b、厚度h，将它们设置为输入参数，输出参数为模型的变形量P4、最大等效应力P5，设定各参数的边界范围对抓手的性能不产生影响。

表3 各优化参数的初始值和变化范围Table 3 Initial values and variation ranges of optimization parameters

RGV抓手尺寸优化是在其满足整体的刚度和强度基础之上进行的，因此抓手进行结构优化时需要对其进行应变分析，使其满足承载需要。之后，根据抓手机械结构的空间尺寸限制，给定设计变量的范围［9］。

本文采用DOE实验设计法来设置样本的数目和设计参数的范围，由此生成了一个设计空间，之后计算出每个样本点对应的输出参数值，多个采样点的输入参数和对应的输出参数就可以构造出一个响应面，该响应面通过三维曲面反映了所建模型的驱动反馈结果，可以通过分析响应面信息来实现对抓手结构的尺寸优化。图7为采用DOE搭建的抓手结构优化设计项目流程图。

图7 RGV抓手结构优化设计项目流程图Fig.7 Flow chart of structural optimization design project of RGV gripper

设计优化实验时，首先要明确与设计参数相关的约束条件和目标函数［10］，如图8所示。

图8 约束条件和目标函数设置Fig.8 Settings of constraints and objective function

3.4 响应面分析

在Design Exploration优化工具中，运用实验设计法设计多组样本实验，不仅能反映输入参数与输出参数之间的动态联系，而且可以分析其他参数对目标参数的影响程度，从而实现对设计参数变量的准确把握。在Workbench中设置了设计变量以及目标函数之后，软件会根据约束条件对其进行迭代计算［11］。通过实验得到的响应优化参数，如表4所示。

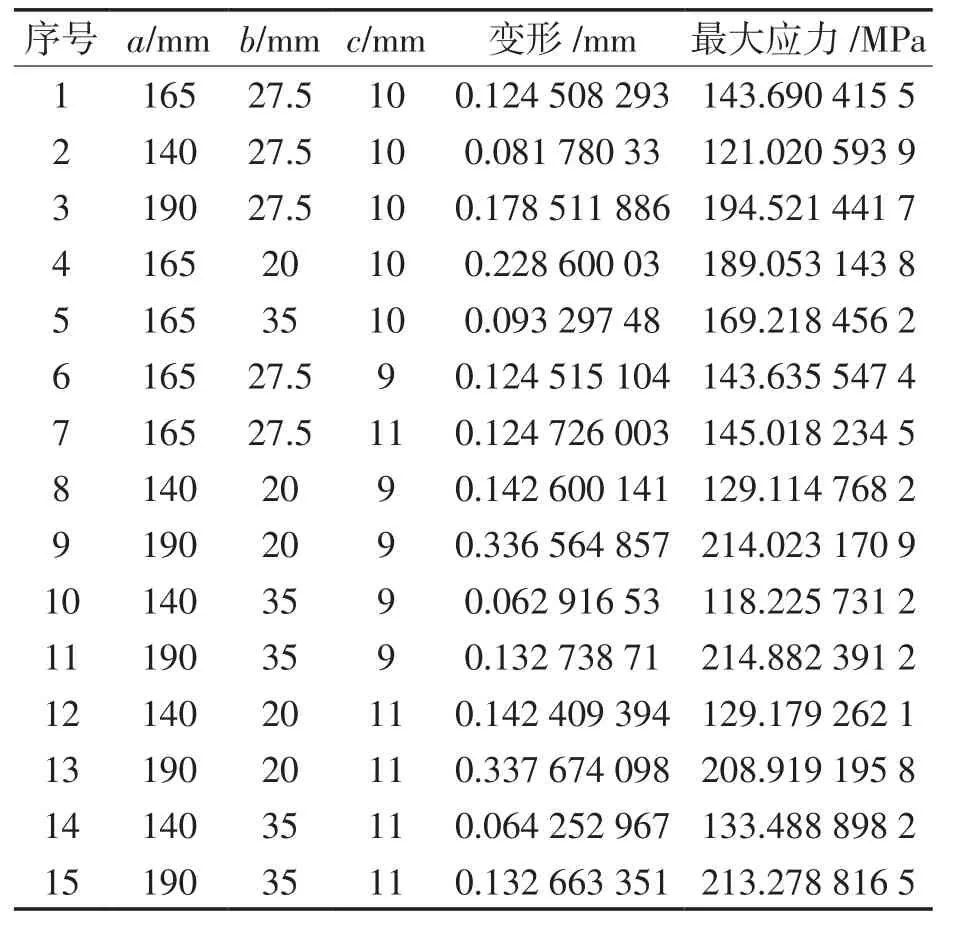
表4 实验得到的响应优化参数Table 4 Response optimization parameters obtained by experiments

在Response Surface Optimization工具中选择DOE模块并设置实验类型为Central Composite Design，样本点设计类型设置为Face-Centered，模型类别设为Standard，更新设计点获得15个样本点，其中，P1、P2、P3、P4、P5分别为抓手的长度、宽度、厚度、变形和最大等效应力。

各输入与输出变量之间的关联均可以通过响应曲线进行描述，P1与P2共同作用时分别对P4和P5的影响、P2与P3共同作用时分别对P4和P5的影响、P1与P3共同作用时分别对P4和P5的影响等，均可以通过响应面表示出来。其中，抓手长度P1与宽度P2共同作用时分别对整体变形量P4和等效应力P5的响应曲线，如图9，图10所示。

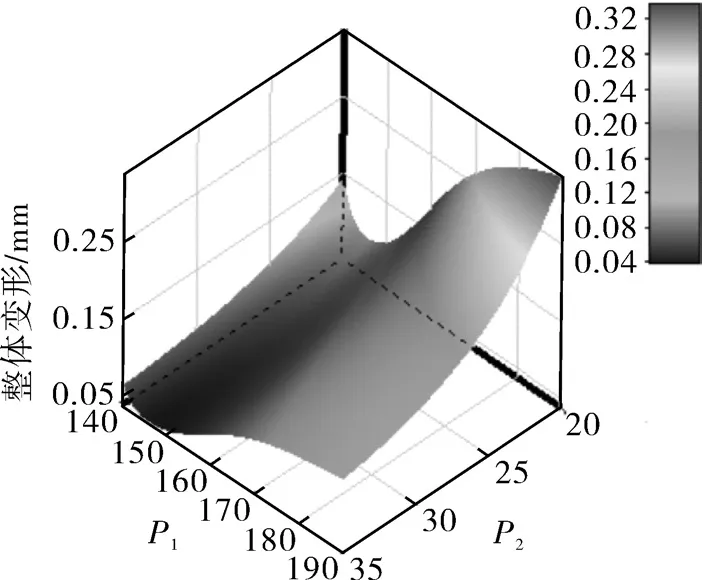
图9 P1与P2共同作用于P4的响应曲线Fig.9 Response curve of P1 and P2 jointly acting on P4

图10 P1与P2共同作用于P5的响应曲线Fig.10 Response curve of P1 and P2 jointly acting on P5

由设计点可知：最小变形为0.062 916 53 mm，最大变形为0.337 674 098 mm，最小等效应力为118.225 731 2 MPa，最大等效应力为214.882 391 2 MPa。

3.5 最优方案选择

由Workbench软件计算各设计点的变形和等效应力，得到如表5所示的三组候选设计方案。由表5可知，相对于方案C，方案A和方案B的等效应力值更小，结果更优。而在满足强度应力条件下，方案B的整体变形量更小，故本文选择方案B作为最优设计方案。

表5 候选方案Table 5 Candidate schemes

将方案B作为最优设计点插入，更新设计点之后，分别对照原模型和现模型的等效应力和整体变形情况，以此来验证优化结果。RGV抓手优化前后的整体变形和最大等效应力云图，如图11所示。

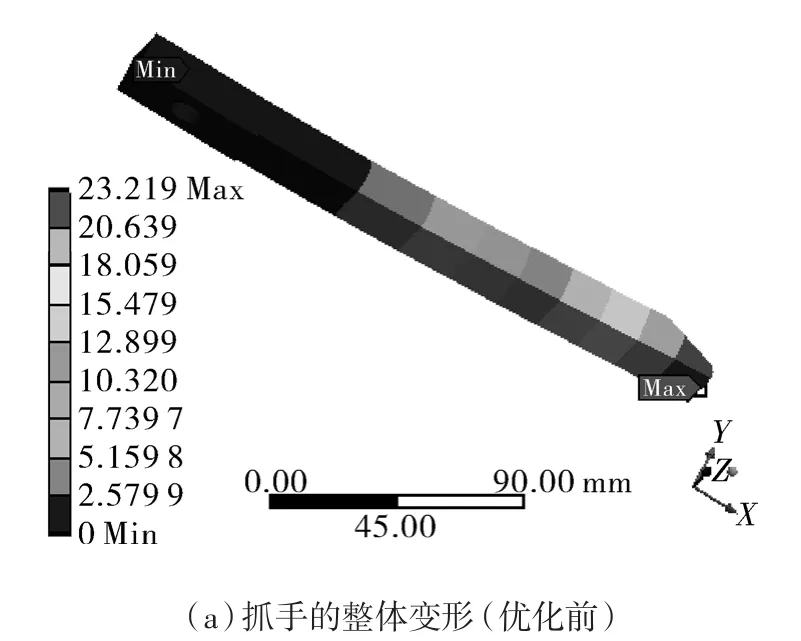
图11 RGV抓手优化前后对比云图Fig.11 Contrast cloud maps before and after optimization of RGV gripper

由云图可知：相较于优化前，优化后的RGV抓手结构参数和性能有了明显的改善，优化前后各参数的对比情况，如表6所示。

表6 优化前后各参数对比Table 6 Comparison of parameters before and after optimization

分析表6可知：优化后抓手的变形量降低了0.287 mm，等效应力减小了93.82 MPa。结果表明：相同承载情况下，优化后抓手的整体变形量和等效应力都有显著的降低，不仅满足了强度和刚度要求，而且使抓手结构尺寸参数更加合理。

4 结语

本文运用ANSYS软件的优化工具Design Exploration，以抓手的关键尺寸为设计变量，以降低抓手的最大等效应力、减小整体变形为优化目标，对取货抓手进行尺寸优化设计，经过分析响应面曲线，得到了抓手关键尺寸与最大等效应力和整体变形之间的关系，从而得到了最佳设计方案。最后，运用ANSYS软件设计实验，将最优方案与初始方案进行对比，结果表明最优方案中抓手的等效应力和整体变形都有显著降低，且抓手的尺寸更加合理。