一种有效降维的特征选择方法及其在水声目标识别中的应用

郭 政，赵 梅，胡长青

(1. 中国科学院声学研究所东海研究站，上海201815；2. 中国科学院大学，北京100049)

0 引 言

在水声目标的识别问题中，提取更多的特征是提高目标识别率的主要方法之一。较高的特征维度包含更为丰富的信息量，可以提高问题描述的准确性。但与此同时，高维特征的冗余信息会影响算法的速度，甚至有可能降低目标识别准确率。因此，根据所需识别数据特性对特征进行选择以降低特征维度是有必要的。

遍历所有特征空间得到最优特征子集的穷举搜索方法是最基础的特征选择算法。但穷举方法效率低下，在面对高维特征向量时计算量巨大。因此需要采取更高效的算法进行特征选择。

通常，特征选择算法可分为过滤式(Filter)算法与封装式(Wrapper)两类算法[1]，两者主要区别为，Filter方法独立于分类识别算法，其优点在于以较小计算量的代价减少特征维数，但并不能保证结果用于分类识别的准确率[2]；Wrapper方法则以分类识别算法的准确率来评价算法性能，虽然计算量较大但准确率较高[3]。在水声目标识别应用中，Wrapper方法作为基础的特征选择算法更为适合。

Wrapper方法中一个关键问题是如何生成待检验特征子集。近年来，学界对此进行了大量研究，例如遗传算法、差分进化算法、粒子群算法、蚁群算法以及模拟其他生物种群行为算法等均可应用于生成、搜索特征子集。Lin等[4]将猫群算法(Cat Swarm Optimization, CSO)应用于参数优化与特征选择。张震等[1]将改进的粒子群算法与禁忌搜索结合应用于入侵检测系统特征选择。Guyon等[5]在应用基因选择研究癌症时提出支持向量机递归特征消除(Support Vector Machine Recursive Feature Elimination, SVM-RFE)算法。Yan等[6]、叶小泉等[7]将其分别与聚类方法等结合应用于特征选择。但各种算法也存在其固有局限性。遗传算法局部搜索性能较差[8]，差分进化算法难以处理噪声问题[9]，粒子群算法在算法后期易于陷入局部最优解[10]，蚁群算法复杂度较高[11]，同属 Wrapper方法的 SVM-RFE能以一定规则对特征进行排序和选择，实现特征降维，但难以有效识别冗余特征，因而只能有限度地提高目标识别准确率[5]。

本文提出一种结合SVM-RFE和CSO的特征选择方法，即SVM-RFE-CSO方法。猫群算法是在粒子群算法(Particle Swarm Optimization, PSO)的基础上发展而来的，将种群分为跟踪及搜寻两种行为模式，通过多次迭代进行寻优。CSO的两种工作模式利用变异算子对自身位置周围进行搜索，并根据最优解位置不断更新猫的当前位置，以跳出局部最优进而得到全局最优解[12]，适合弥补SVM-RFE难以有效识别冗余特征的局限性。因此，将 CSO与SVM-RFE进行结合，并将其应用于水声目标识别的特征选择中，可取得较好的效果。

1 基本算法原理

1.1 支持向量机递归特征消除(SVM-RFE)算法

Guyon等[5]对SVM进行综合考察，在此基础上提出对特征进行排序的SVM-RFE特征选择算法。SVM核心思想是建立一个决策曲面[13]：

以最大化分类间隔。在非线性情况下，引入松弛变量，目标函数可表示为

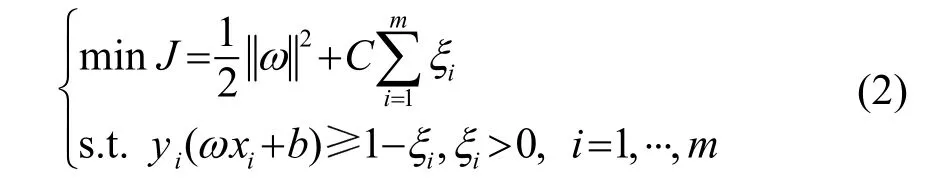
若移除第i个特征，对目标函数的影响根据泰勒展开有：

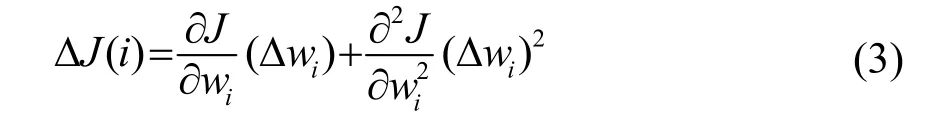
则对于目标函数J的最优解，可只考虑二阶，因此有：

故在决策函数中特征的权值w大小表示了其包含信息量的多少，在SVM-RFE中则以w2表示特征的重要程度，作为特征排序的依据。SVM-RFE算法的流程如图1所示。

图1 SVM-RFE算法流程图Fig.1 Flow chart of the SVM-RFE algorithm

图1中，S表示当前特征列表索引序列，R表示执行完毕后输出的特征排序列表索引序列，∅表示空集。R中特征权值依次递减，根据特征重要性对其进行排序。本文在此基础上做进一步处理，根据R定义一组特征子集F1,··,Fm，其中前一个子集含于后一个子集中，且第m个子集包含权值最高的m个特征，即F1包含最重要的特征参数，F2包含最重要及次重要的特征参数，以此类推。之后综合考虑识别准确率及对特征维数的需求选出特征子集，完成特征选择。在目标识别中，本文采用SVM作为目标识别分类器，将特征选择后确定维度的特征向量由原始空间映射到高维空间，并在高维空间构造决策函数，以RBF核函数替代内积来简化运算。

SVM-REF特征选择算法以特征对分类器的作用为依据计算特征权重，但对特征本身是否冗余欠缺考量[14]。在实际应用中，存在经过SVM-REF选择后的M维非连续特征较N维连续特征的目标识别率没有提升的情况(M＜N，且特征按重要性由高至低选取)。因此，SVM-REF特征选择算法在降低特征维数和选择较高识别率的特征子集方面均有所局限，并不能给出最优解，需加以改进。

1.2 猫群算法(CSO)

猫群算法通过模仿自然界中猫群的行为，将其行为模式分为跟踪模式及搜寻模式，通过定义两者的比例关系(Mixture Ratio, MR)确定猫的分配模式进行寻优[15]。算法流程如图2所示。

图2 猫群算法流程图Fig.2 Flow chart of the CSO algorithm

图2中，搜寻模式设定4个基本要素：记忆池(Seeking Memory Pool, SMP)、搜寻维度范围(Seeking Range of the Selected Dimension, SDR)、维度改变量(Counts of Dimension to Change, CDC)、自身位置判断(Self Position Consideration, SPC)。首先创建N=PSM个当前猫的位置副本，根据SPC值确定SMP中保留的候选位置，再由CDC值对每个副本加或减，根据 SDR以一定比例确定增减值以替换其位置值，并根据式(5)计算待选位置可能性，之后据此选择位置点替换当前猫的位置。

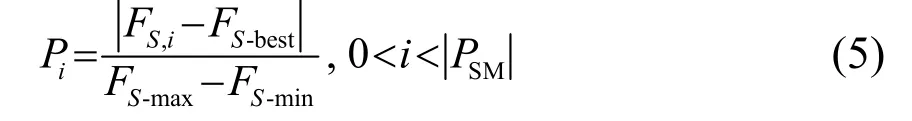
式中，Pi为待选位置可能性；FS,i为适应度；FS-best为最优适应度；PSM为记忆池个数。

根据MR确定分配模式后，对分配搜寻模式的个体标志位置 1。跟踪模式则是根据全局最优位置更新猫当前速度，然后根据新的速度确定猫的当前位置。速度及位置更新方法如式(6)、(7)所示：

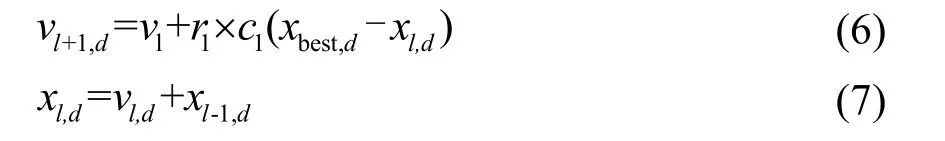
式(6)、(7)中：xl,d表示猫l第d维的当前位置，xbest,d表示猫群中最大适应度第d维的对应的位置点，r1为常量，c1表示通常取值范围为[0, 1]的变量，猫群总维度为D，d≤D。

2 SVM-RFE-CSO算法

SVM-RFE算法在实现有效降维的同时存在一个缺陷，即难以较好地利用冗余特征，因而最后筛选出的特征子集未必是最优性能特征子集。本文利用CSO搜索最优解的能力，对SVM-RFE加以改进。改进后算法流程如图3所示。

图3 SVM-RFE-CSO算法流程图Fig.3 Flow chart of the SVM-RFE-CSO algorithm

SVM-RFE-CSO算法实际分两步进行特征选择。首先进行 SVM-RFE，筛选出部分优秀特征子集作为部分初始种群，并加入随机生成种群个体作为初始种群，而后应用 CSO 进行迭代计算，选出最优特征子集，完成特征选择。

在判断每次迭代生成的新的个体是否更优时，可应用适应度函数对其进行评价。通常适应度函数ffit由目标识别准确率与特征维数两个变量来确定：

式(8)中：ffit表示适应度函数，Rauc表示目标识别准确率，ddim表示特征选择后的特征维数，A、B分别为目标识别准确率和特征维数的权重参数。在评价迭代后的个体时，目标识别准确率与特征维数并非两个孤立的变量，因而为保证两者关联性，将式(8)修正为式(9)：

本文进行特征选择的目的为在保证目标识别准确率的基础上对特征降维，以选出最佳特征子集作为目标识别的特征向量，故在参考其他工作[1]的基础上选取A=0.95进行计算。

3 算例验证

为直观说明SVM-RFE算法及CSO算法在本文算法中所起到的作用，以罗德岛大学等机构公开的“Discovery of Sound in the Sea-Anthropogenic Sounds”数据[16]为例，分别应用 SVM-RFE、CSO及SVM-RFE-CSO方法进行特征选择，将得到的特征向量应用于目标识别，并对比识别结果。

所使用的数据集包括4类共170个样本，样本特征向量维数m=10。图4为应用SVM-RFE进行特征选择的结果，对应维数的识别准确率表示经SVM-RFE处理后由排序靠前的m个特征组成的特征子集识别准确率。当m=6时，准确率为90.70%，达到最高值。可见SVM-RFE能快速得出优秀的特征子集，起到特征降维效果。图5为应用CSO及SVM-RFE-CSO进行特征选择的结果。由图5可知，两者识别准确率均随迭代次数上升而升高，CSO 方法依次达到 86.05%、88.37%和 90.70%，SVM-RFE-CSO方法快速达到 90.70%后即不再升高。可见 CSO能起到跳出局部最优值继续寻优的作用，SVM-RFE-CSO相比CSO可更快达到最优值。此外，数据集原始特征维数较低会使计算过程更简单，这也说明SVM-RFE-CSO在特征维数较高、计算过程更复杂的情况下才具有更明显的优势，在第4节中将重点分析该种情况。

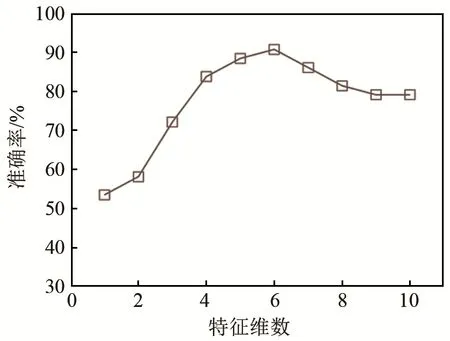
图4 识别准确率随特征维数变化(处理数据取自文献[16])Fig.4 The variation of recognition accuracy with the dimension of feature vectors (processed data from Ref. [16])

图5 识别准确率随迭代次数变化(处理数据取自文献[16])Fig.5 The variation of recognition accuracy with the number of iterations (processed data from Ref. [16])

此外，在寻优计算过程中对适应度函数中权重系数A的取值进行了验证，取A=1时可保证特征选择后识别准确率达最高值 90.70%，因此在后续的计算中取A=1。

4 水声目标识别实验

4.1 实验数据获取

为验证算法在水声目标识别中的应用效果，选取2018年6月某次取的6种舰船辐射噪声信号进行目标识别。

4.2 目标特征提取

首先进行样本的特征提取。信号采样频率为32 kHz，6种不同水声目标均取100段时长为 s的信号作为样本。数据集具体信息如表1所示。

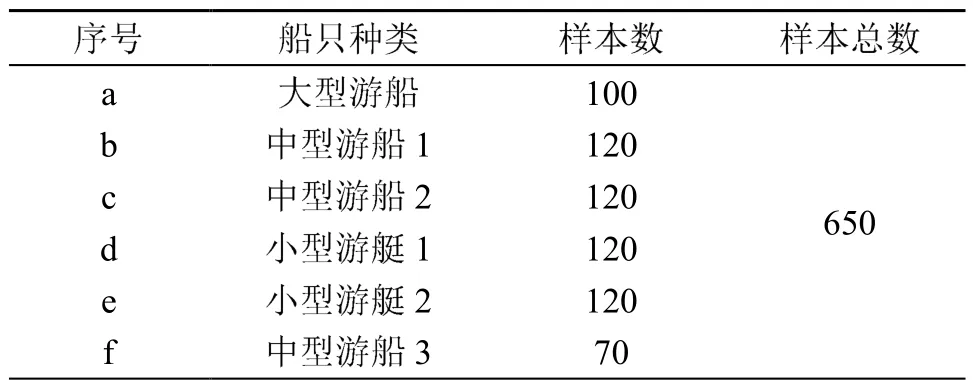
表1 水声目标(船只)辐射噪声样本信息Table 1 Sample information of radiation noise from underwater acoustic targets (ships)

梅尔频率倒谱系数(Mel-Frequency Cepstral MFCC)是一种基于人耳听觉特性的目标特征参数，其在频域上以Mel频谱为标度，模拟了人耳听觉对频率识别的非线性特点，并描述了目标辐射噪声在不同频段上的声学特性[17]。

MFCC的提取首先要经过数据预处理，将信号分帧加窗，而后经 FFT计算出每帧数据的频谱参数，并将每帧频谱参数通过数量为M的三角带通滤波器组成的Mel频率滤波器组，之后对每个滤波器输出取对数，得到M个对数能量参数S(m)，m= 1 ,2,···,M。最后对这些参数做离散余弦变换，即得到目标的MFCC，如式(10)所示[18]：

图6所示即为不同水声目标辐射噪声的MFCC计算结果，其中图6(a)～6(f)分别对应表1中不同的水声目标。可见，不同种类水声目标的MFCC存在差异，可作为目标识别的依据。将MFCC按帧数求平均，结果如图7所示。对比图7(a)～7(f)可见不同种类水声目标的 MFCC求帧数平均后依然保持了较好的区分度，因此，计算水声目标辐射噪声的30维MFCC帧数平均作为特征向量，用于特征选择及目标分类识别实验。

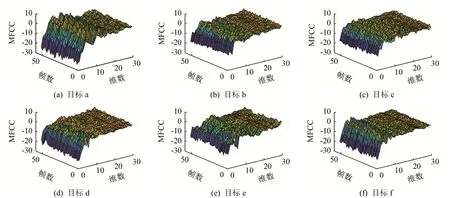
图6 不同水声目标辐射噪声的MFCCFig.6 MFCC of different underwater acoustic targets

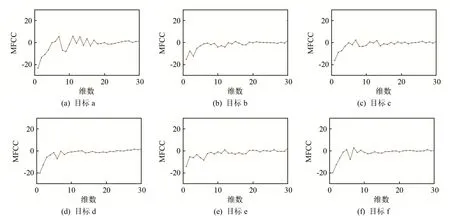
图7 不同水声目标辐射噪声的MFCC帧数平均Fig.7 MFCCs’ frame average of different underwater acoustic targets

4.3 数据分析与结果

在水声目标识别的实际应用场景中，通常在进行由原始信号提取目标信号的处理后也难以完全消除本底噪声干扰。通过控制信噪比RSN对信号添加背景噪声来模拟这种情况：

式(11)中：vnoise表示噪声时域幅值，vsignal表示信号时域幅值。在后续处理过程中，对舰船辐射噪声样本添加高斯噪声至RSN=0 dB。

经SVM-RFE特征选择后，输出最优特征子集维度的选择对下一步特征选择及分类结果有一定影响[14]。为分析经SVM-RFE特征选择后得出的特征子集对算法结果的影响，分别应用 SVM-RFE、CSO、SVM-RFE-CSO算法进行特征选择，结果如图8、9所示。

图8 高斯噪声背景下水声目标识别准确率随特征维数变化Fig.8 The variation of underwater acoustic target recognition accuracy with the dimension of feature vectors under Gaussian noise background

由图8可见，目标识别准确率与经SVM-RFE特征选择后的特征子集维度m大致呈正相关，但并非特征子集维度越大目标识别准确率越高。m＜16时目标识别准确率随特征子集维度m的增加而升高，当m=16时准确率即达到最大值，而m＞16时准确率随特征子集维度m的增加而呈降低趋势。据此可判定前 16维特征中包含了可用于目标识别的大部分有效信息，但不排除另外14维特征中也包含对准确识别目标有正向作用的有效信息。因此，在SVM-RFE特征选择后续处理中特征子集最高维度可由此确定，并剔除排序靠后的特征。

图9为CSO算法与SVM-RFE-CSO算法进行特征选择过程中每一代最优特征子集的目标识别准确率。可见经过相同次数的迭代，SVM-RFE-CSO算法相比 CSO算法，因初始特征子集更优而达到了更高的目标识别准确率。

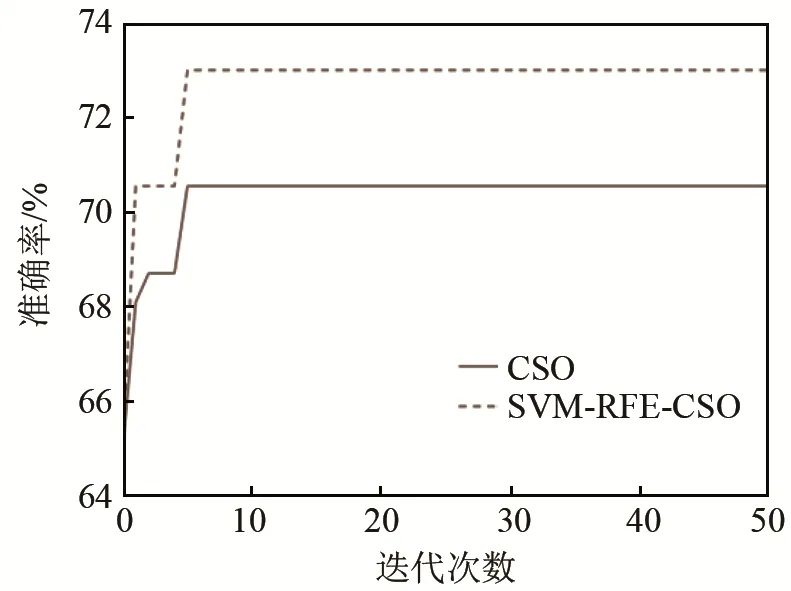
图9 高斯噪声背景下水声目标识别准确率随迭代次数变化Fig.9 The variation of underwater acoustic target recognition accuracy with the number of iterations under Gaussian noise background

为了说明 SVM-RFE-CSO算法性能是否有改进，在Intel i5-9330H CPU、8G RAM的计算机环境下，取每一代个体数N=20、迭代次数I=50作为参数组合1，取N=5、I=30作为参数组合2，分别重复10次特征选择实验，结果如表2所示。由表2中的结果可见，经SVM-RFE处理及参数组合1、2情况下CSO算法处理后得出的10次平均准确率分别提高了5.52、5.71和3.13个百分点，最优子集维数分别下降了14、15.6和15.8；参数组合1情况下SVM-RFE-CSO处理后得出的 10次平均准确率相比SVM-RFE算法及CSO算法分别提高了1.17、0.98个百分点；参数组合2情况下SVM-RFE-CSO处理后得出的10次平均准确率相比 SVM-RFE算法及CSO算法分别提高了21.48、3.87个百分点，最优子集维数分别下降3.5、1.9和0.6、-1.2，而参数组合1、2情况下SVM-RFE-CSO算法10次平均用时为121.62 s和17.50 s，相比CSO算法10次平均用时118.60 s和17.67 s差距很小。综合考虑两种参数组合，对比本文提出的方法和分别单独使用SVM-RFE方法及CSO方法，文中提出的方法在平均特征维数降低 8%的基础上，平均目标识别率提高了1.88%。在排除了随机性的前提下，算法性能得到了提升。对比两种参数组合情况可知，通过调整参数，可改变SVM-RFE-CSO特征算法的降维效果、选出特征子集的识别准确率和计算时长，其综合性能优于单一CSO算法和SVM-RFE算法。

表2 未经选择全部特征及不同处理方法10次平均结果对比Table 2 Comparison of 10-time average results of all features and different processing methods

5 结 论

本文在分析SVM-RFE算法及CSO算法的基础上，针对SVM-RFE特征选择方法难以有效识别冗余特征的局限性，提出了一种结合两者优势的特征选择算法。

文中提出的算法利用 CSO算法的寻找全局最优的特点，解决SVM-REF算法中特征维数降低及目标识别准确率提高有限的问题，在保证目标识别准确率的前提下，实现有效降维。此外，通过水声目标识别实验进行了验证，改进后的 SVM-REFCSO特征选择算法相比于单一 SVM-RFE算法及CSO算法，均提高了目标识别准确率，且相比CSO算法并未大幅提高运算时长。最后，本文提出的特征选择算法除有效降低特征向量维度、提高目标识别准确率外，在验证用于目标识别的新特征的性能时，对于判断该特征是否适合用于此场景下目标识别也有一定应用价值。下一步还需进行最优参数选取的研究，以充分发挥算法性能。