基于广义局部曲率模态信息熵和BP神经网络的结构损伤识别方法

项长生, 原 子, 周 宇

(1. 兰州理工大学 土木工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心, 甘肃 兰州 730050; 3. 安徽建筑大学 土木工程学院, 安徽 合肥 230601)

近年来在桥梁损伤识别领域,国内外学者做了大量的研究.桥梁结构损伤识别的方法可以归纳为以下几种：模型修正法[1]、动力指纹识别法[2]、拟静力法[3]、基于信号处理的损伤识别法(如信息熵[4-5]、小波变换法[6]等)以及神经网络法[7]等.

熵是混乱程度的相对量度,通常,它用于描述系统复杂性.近年来有学者采用信息熵来进行损伤识别,Li[4]将信息熵与柔度矩阵等指标相结合,通过遗传神经网络和D-S证据理论对一斜拉桥进行损伤识别.Yang[8]定义了基于位移的广义局部信息熵的概念,将损伤处局部损伤“放大”从而取得了良好的识别效果.毛福超[9]利用基于位移的广义局部信息熵识别了一简支梁桥的相对损伤位置和相对损伤程度,但没有定量地识别损伤.信息熵因其计算简单、对环境噪声不敏感等优点[10]在桥梁损伤识别中得到了广泛的应用,然而目前基于广义局部信息熵的损伤识别方法在桥梁损伤识别中应用较少.

桥梁结构中的损伤定位和损伤定量可以被视为“模式匹配”一类的问题.神经网络本身所具备的非线性映射及联想扩展的能力,使得其适用于这种模式匹配类的问题.同时,神经网络的输入参数决定了损伤识别的精度和效果[11].其中,曲率模态在结构损伤识别中是一个优良的指标,其优点在于不需要无损状态下的信息就可以准确判别损伤位置,但同样不能定量地确定损伤程度[12-13].有些学者[14-16]将曲率模态作为神经网络的输入参数识别损伤并发现当损伤位置接近结构某阶振型的节点时,该阶曲率模态振型便难以对损伤状态做出正确的判断.

因此,针对曲率模态在振型节点处识别精度不足及无法进行准确损伤定量的问题,本次基于广义局部曲率模态信息熵和神经网络对简支梁进行损伤识别,并对该指标的有效性进行研究.

1 曲率模态基本理论

曲率模态这一概念由Pandy[17]在1991年提出.根据振动理论,梁的横向无阻尼自由振动微分方程为

(1)

式中：y(x,t)为t时刻梁轴线任意一截面x处的横向振动位移；EI(x)为梁的抗弯刚度；m(x)为梁的单位长度质量.根据模态理论,式(1)的解可以表达为模态叠加的形式：

y(x,t)=∑φi(x)qi(t)

(2)

式中：φi(x)和qi(t)分别为位移模态振型和模态坐标.

根据材料力学理论中弹性梁弯曲变形曲线的曲率与位移的关系,可得任意截面x处结构弯曲振动曲线的曲率变化函数为

(3)

由式(3)可见,曲率变化函数v(x)与曲率模态振型φ″i(x)幅值成正比.对于梁结构,承弯结构曲率变化函数与其力学参数的基本关系为

(4)

式中:下标i为截面位置；vi为曲率；Mi为弯矩；EiIi为梁的弯曲刚度.

从式(4)中可以看出,梁的弯曲刚度与对应点的曲率成反比,即曲率能够反映刚度的变化.曲率模态在试验中不能获得,但可以通过对位移模态进行适当变化得到.根据数学曲率公式对位移进行差分可得

(5)

式中：yi为i点的模态位移;h为测点间距.

2 广义局部曲率模态信息熵的推导

信息熵这一概念最早由Shannon[18]提出,并给出了信息熵的公式：

H=-pilnpi

(6)

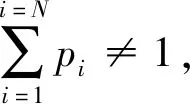
(7)

则i点的广义局部曲率模态信息熵可以由下式表示：

Hgvi=-pilnpi

(8)

式(7)中因N取值越大,则计算中靠近支座处由于数据不完整而导致无法计算的节点越多,因此取N=3.则可以得到

(9)

将pi带入式(8)则得到广义局部曲率模态信息熵的计算公式：

(10)

即利用式(10)计算广义局部曲率模态信息熵并以此指标对结构进行损伤识别.

将式(9)代入式(8),绘制曲线如图1所示,其中横坐标为局部概率pi,纵坐标为相应熵值.由式(9)可知,局部概率pi的取值范围为pi∈[0.1],且当pi>1/e时Hgvi为减函数；pi<1/e时Hgvi为增函数.本例中pimax≈0.35<1/e,因此式(9)在[0,pimax]单调递增.利用差分法计算广义局部曲率模态信息熵时,在损伤附近节点的相对信息量会有不同的增减幅波动,在pi由0→pimax的过程中指标Hgvi的斜率不断减小,这导致在[0,pimax]内,指标熵减特征更为明显,且随着损伤程度的增加,损伤处附近节点的相对信息量增减幅值更为明显.基于指标在定义域的以上几点特性,利用该指标对损伤位置和程度进行判别是可行的.

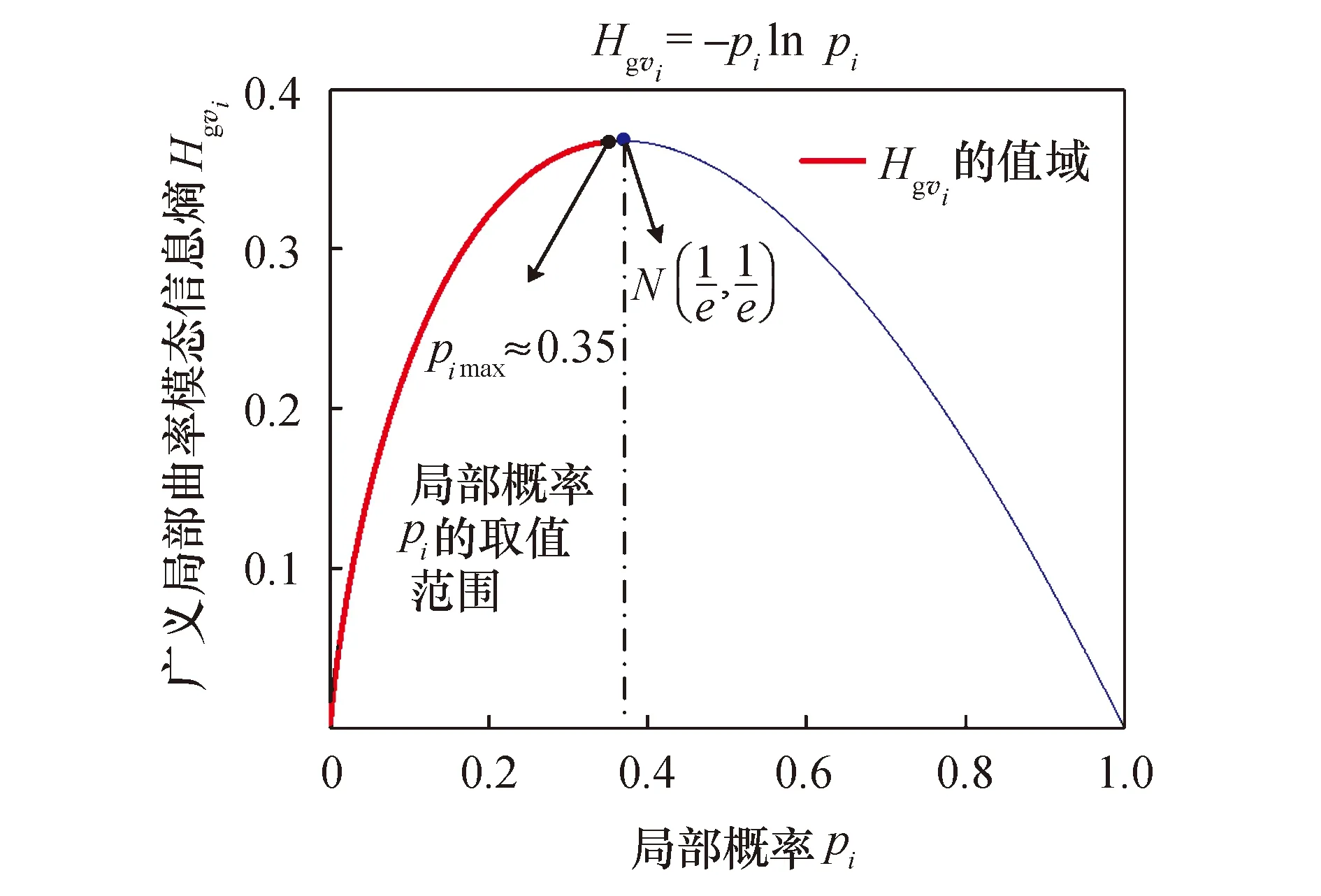
图1 指标的定义域和值域Fig.1 The domain and value range for the indicator

3 基于广义局部曲率模态信息熵对简支梁桥的损伤识别

3.1 模型建立

以一简支梁为例,该梁的全长L=32 m,设计截面为箱梁截面,见图2.简支梁主梁采用C50混凝土,材料属性：弹性模量E= 3.4500×107kN/m2;泊松比为0.2.利用有限元软件Midas civil建立简支梁有限元模型如图3所示.该简支梁沿长度方向划分为等长的32个单元,每个单元长度为1 m.

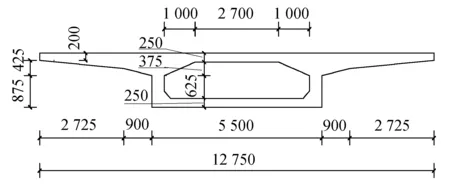
图2 箱梁横截面(mm)Fig.2 The cross section of the girder (mm)

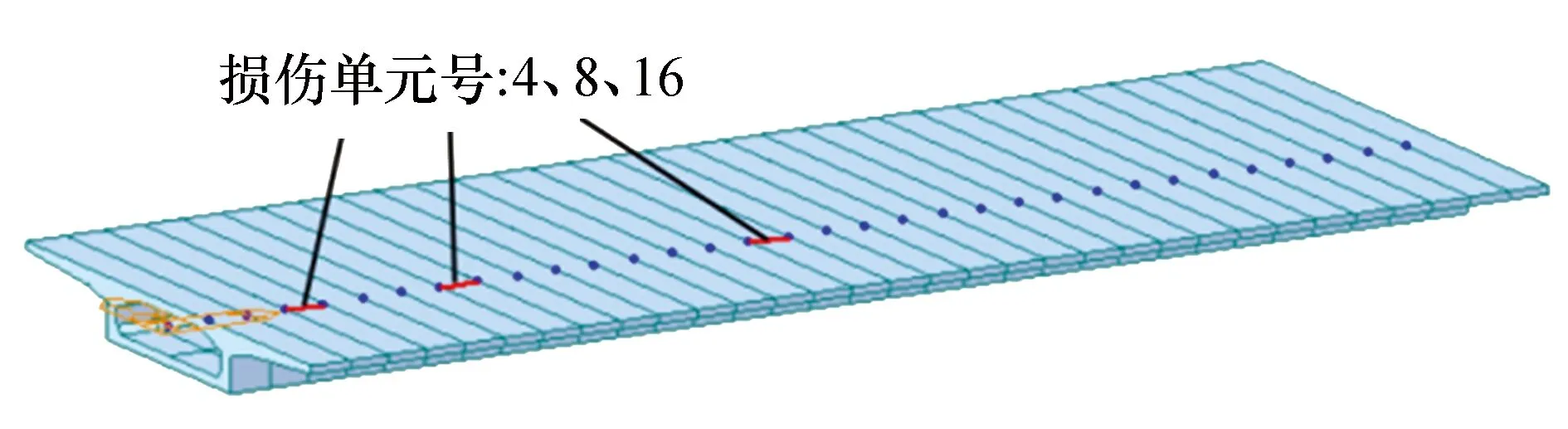
图3 简支梁及模拟损伤位置Fig.3 The simply supported beam and damage locations for simulation

3.2 损伤工况

利用刚度折减法[19],通过弹性模量E的下降来模拟损伤,其中损伤位置分为跨中、1/4跨和1/8跨3种情况,对应的损伤单元号为4、8、16；每处损伤位置对应的损伤程度分别为30%、25%、20%、15%、10%五种情况.15种损伤工况见表1.

表1 损伤工况模拟Tab.1 Cases for damage simulation

4 BP神经网络损伤识别结果

在实际工程中,由于建筑材料的非线性与工程结构的复杂性等因素,导致动静力特性的变化与结构损伤或者外界作用之间的关系很难用严格的数学表达式表达出来[20].对于这类模式匹配来解决损伤识别的问题,BP神经网络应用较为广泛.其工作机理为：给定误差阈值后,将未达到阈值的误差反向传播,并不断调整优化各个神经元之间的连接权值,以期最后达到识别精度从而进行损伤识别.已有研究表明,任何一个连续函数都可以用一个3层的BP神经网络来表达.

4.1 神经网络的构建及损伤位置识别结果

采用3层BP神经网络,将除工况三、八、十三外的其余工况下结构各个节点的曲率模态和广义局部曲率模态信息熵作为神经网络的训练样本,其中,神经网络训练函数采用trainlm函数,2个神经网络经三分法[21]确定隐含层节点数最优为11,以归一化识别结果为输出参数,若输出结果为[1,0,…,0,0],则代表第一点有损伤,且输出节点为32维.基于以上方式,以曲率模态为输入参数的神经网络构造为31-11-32；基于广义局部曲率模态熵的输入参数因式(7)中N=3,输入参数为30维,因此网络构造为30-11-32.训练最大迭代步数均为50,训练精度均为10-7.

以上述2种指标作为神经网络输入参数的识别结果见表2、表3.

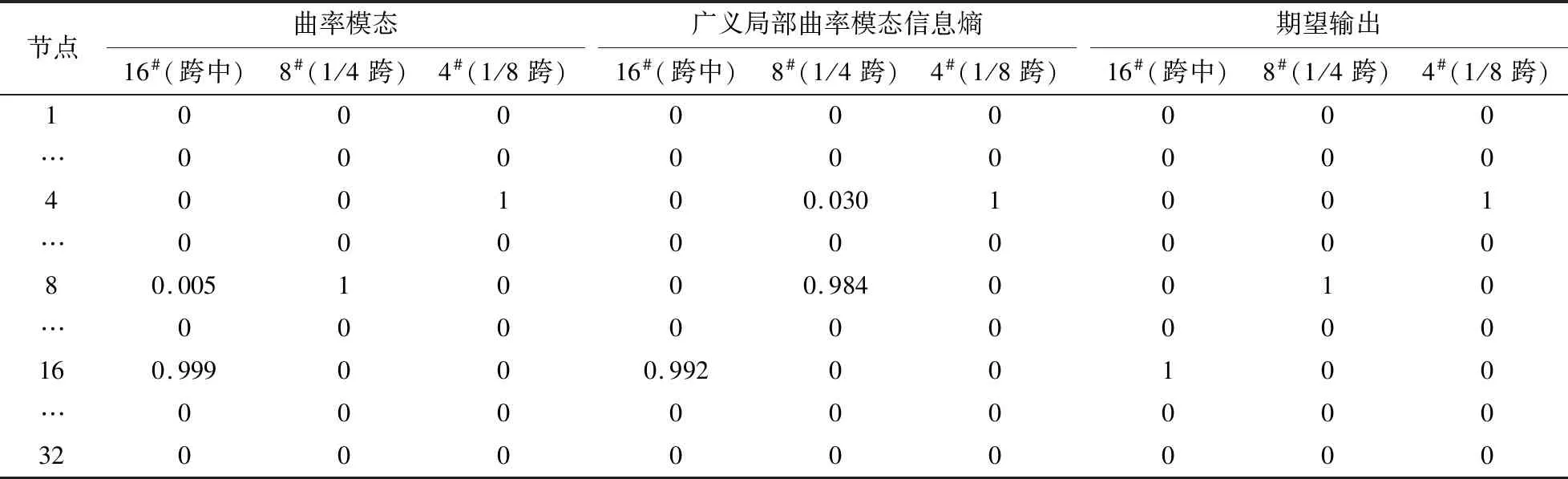
表2 损伤位置识别结果Tab.2 Identified results of damage location

表3 损伤程度识别结果Tab.3 Identified results of damage degree

由表2可知,曲率模态精度略高于广义局部曲率模态信息熵,广义局部曲率模态信息熵最大误差仅为1.6%.因此2种指标均能较好地识别损伤位置.

4.2 神经网络的构建及损伤程度识别结果

损伤定量时采用3层BP神经网络,在损伤定位的识别结果基础上,损伤位置处及其前后两节点的曲率模态和广义局部曲率模态信息熵作为神经网络的输入参数,将损伤后残余刚度作为输出参数.根据三分法试算该神经网络的最优隐含层节点数为5,因此神经网络的构造为2-5-1,且训练最大迭代步数均为50,训练精度为10-7.得到的训练结果见表3.

神经网络的识别结果取3位有效数字.根据表3可以看出,在同样的神经网络构造及训练参数下:

1) 广义局部曲率模态信息熵的总体识别结果要优于曲率模态：曲率模态的平均误差为5%,广义局部曲率模态信息熵的平均误差为2.8%；

2) 曲率模态识别损伤程度的精度随着损伤位置靠近振型节点(支座处)而降低：曲率模态指标在跨中部位的绝对误差为1.88%,优于广义局部曲率模态信息熵的2.88%,但在靠近振型节点处的1/4跨和1/8跨处,损伤识别的相对误差达到了4.88%和8.25%；

3) 广义局部曲率模态信息熵在靠近支座处的损伤识别精度要优于曲率模态的识别精度：在1/4跨和1/8跨处,识别的相对误差仅为1.38%和4.13%,优于曲率模态指标；由于该指标体现“局部”特征的特性,其对于局部损伤有“放大”效果,因此损伤的位置对其识别效果的影响不明显.

5 测点数量对广义局部曲率模态信息熵识别效果的影响

为了研究测点数量对广义局部曲率模态信息熵识别效果的影响,将单元数目扩展为64和128,并提取各个节点的参数,损伤工况不变.将3种测点数量下损伤识别结果绘制如图4～12所示.

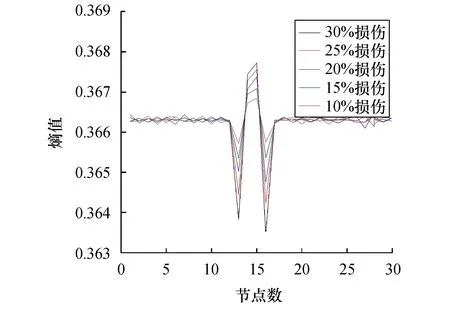
图4 测点数为33时跨中损伤识别结果Fig.4 Identified results out of 33 measuring points at mid-span

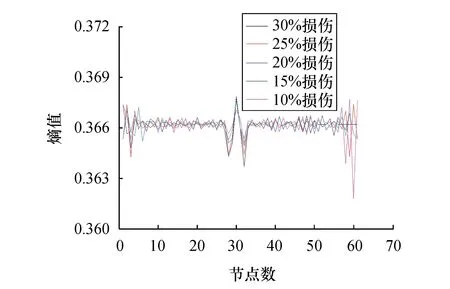
图5 测点数为65时跨中损伤识别结果Fig.5 Identifying results out of 65 measuring points at mid-span

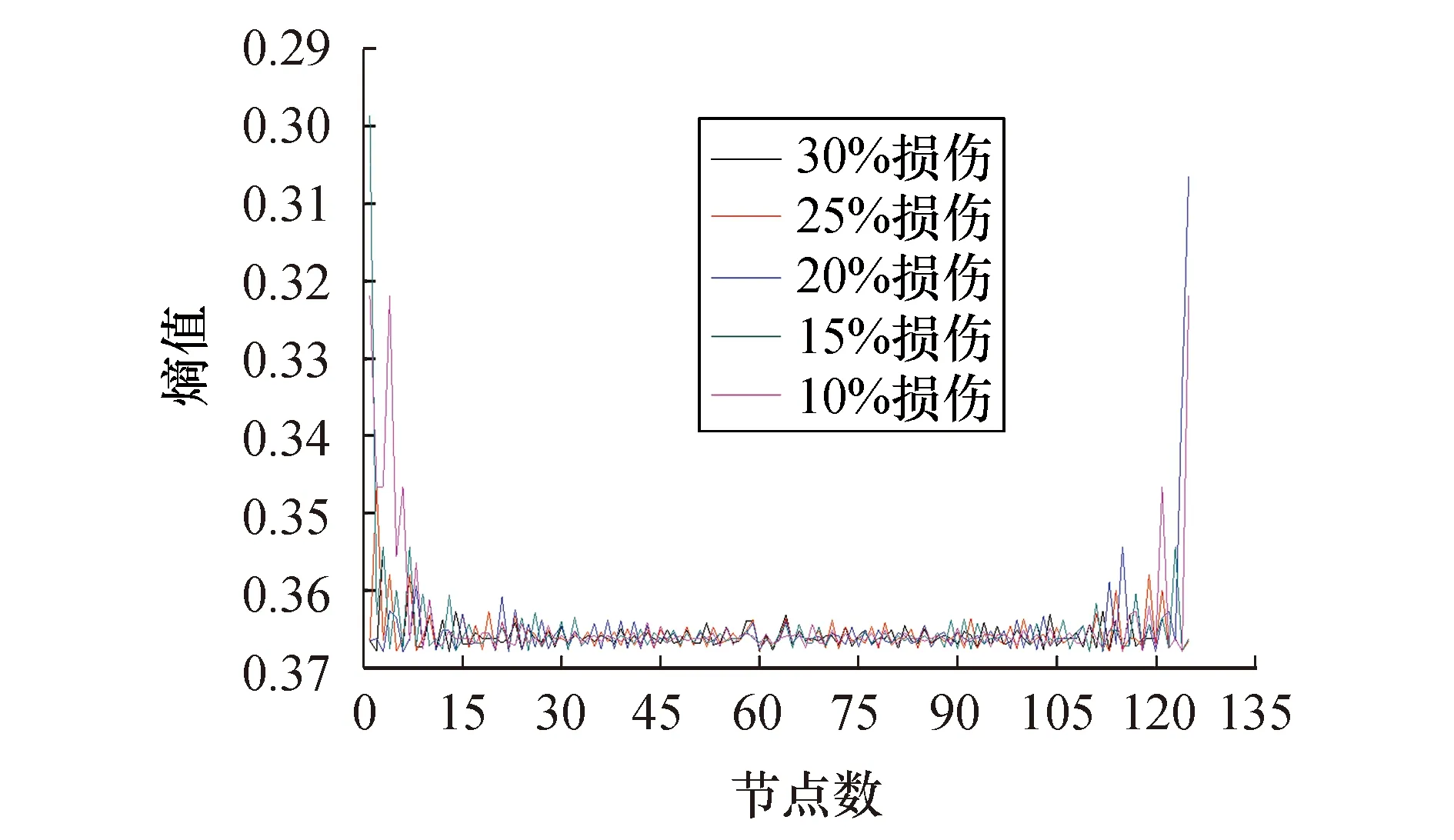
图6 测点数为129时跨中损伤识别结果Fig.6 Identified results out of 129 measuring points at mid-span

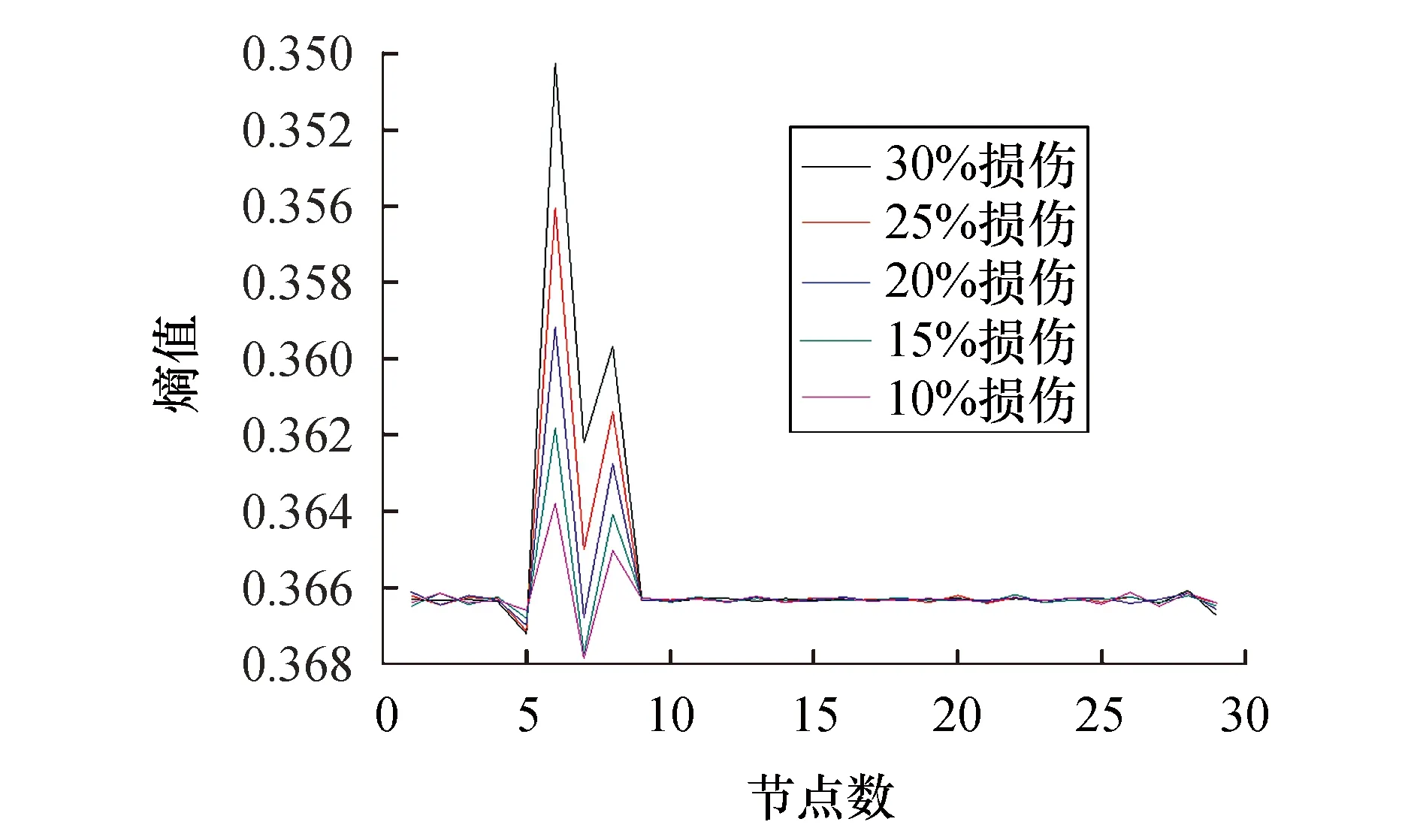
图7 测点数为33时1/4跨损伤识别结果Fig.7 Identified results out of 33 measuring points at 1/4 span

图8 测点数为65时1/4跨损伤识别结果Fig.8 Identified results out of 65 measuring points at 1/4 span

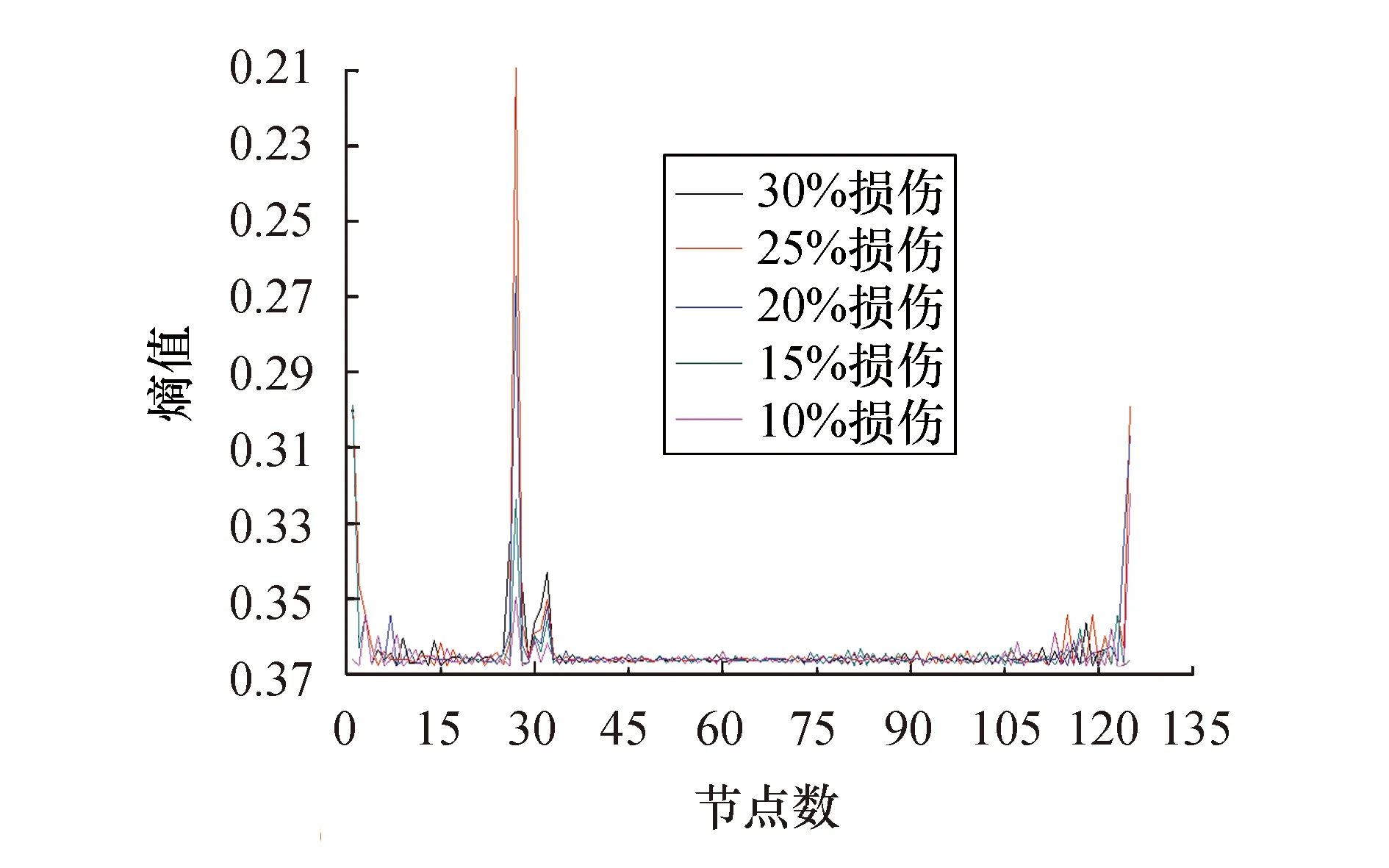
图9 测点数为129时1/4跨损伤识别结果Fig.9 Identified results out of 129 measuring points at 1/4 span

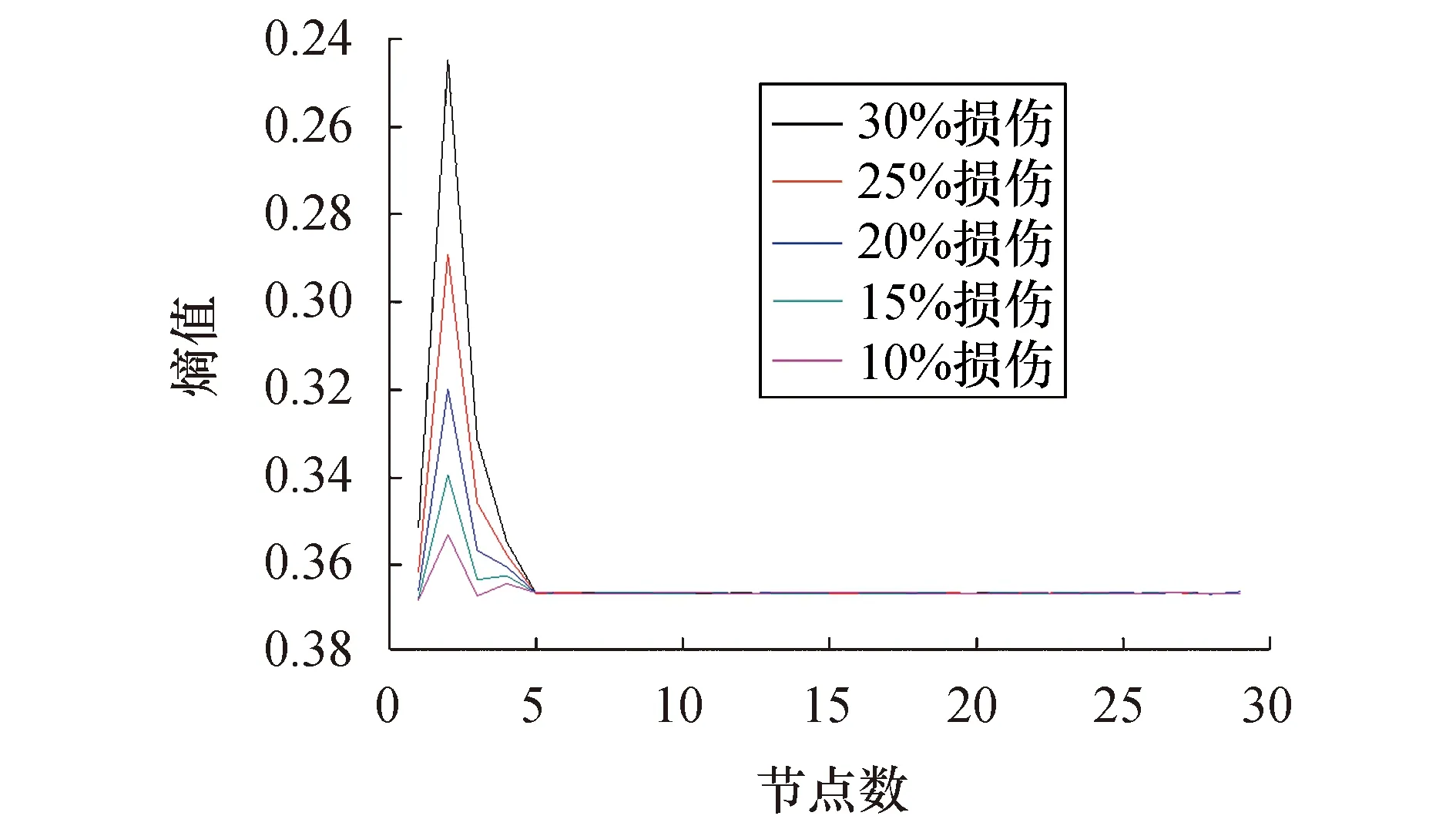
图10 10测点数为33时1/8跨损伤识别结果Fig.10 Identified results out of 33 measuring points at 1/8 span

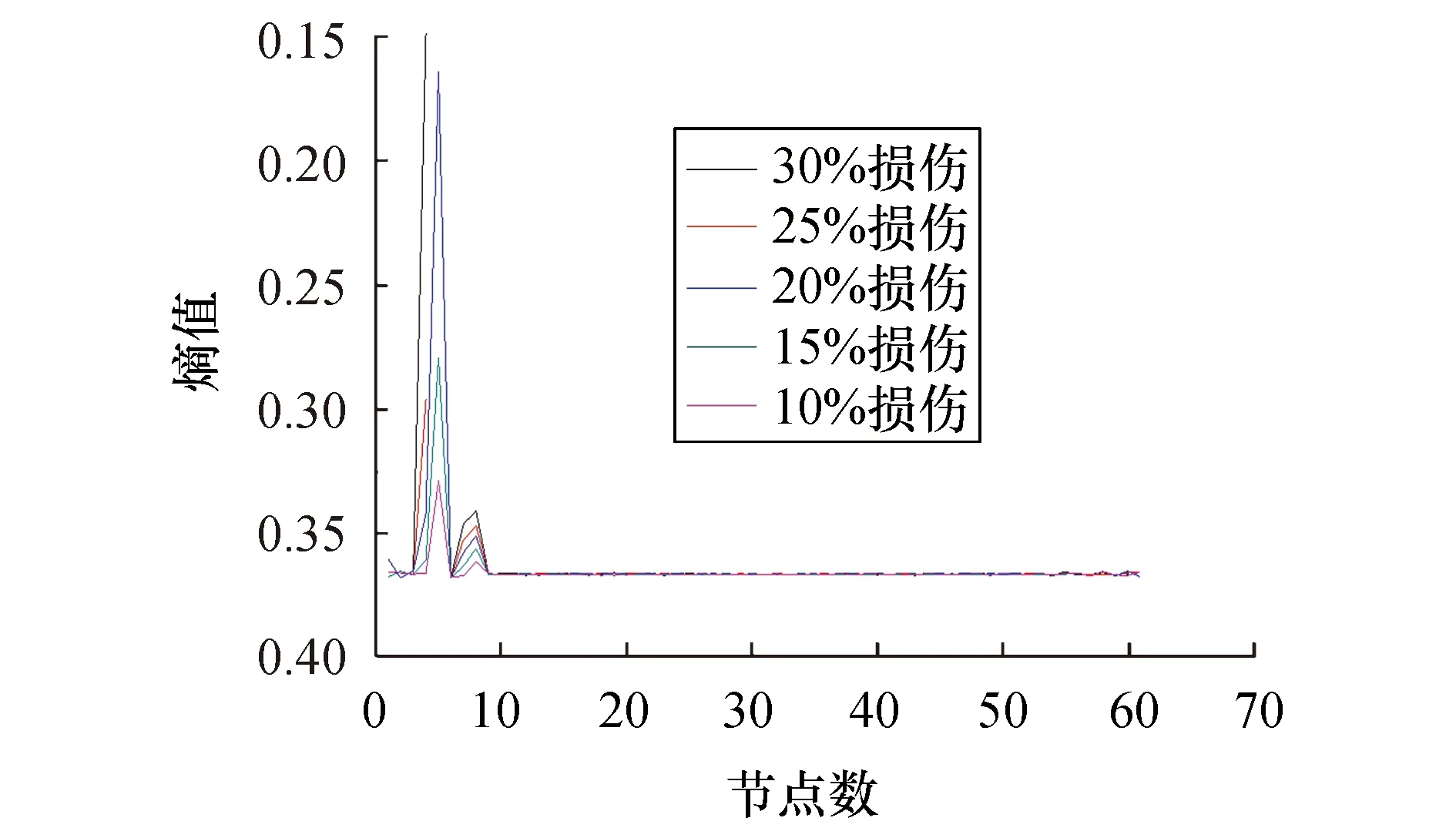
图11 测点数为65时1/8跨损伤识别结果Fig.11 Identified results out of 65 measuring points at 1/8 span

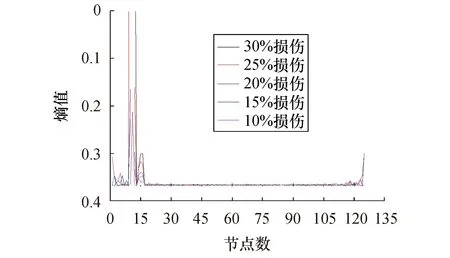
图12 测点数为129时1/8跨损伤识别结果Fig.12 Identified results out of 129 measuring points at 1/8 span

对比图4～12可以看出：

1) 不同损伤位置下,在节点数量为33时损伤位置和损伤程度总体效果最好,在损伤处指标峰值较为明显且随着损伤程度增加其熵值减小并呈一定规律；

2) 在测点数量为65和129时,损伤处有超出指标值域或无法计算的峰值,峰值处相差较大且指标不连续,同时损伤程度并不呈现一定的规律性,这对利用神经网络判定其损伤程度是不利的；

3) 跨中处该指标对于测点数量改变的影响尤为敏感：随着节点数量增加至129,该损伤指标渐渐被湮没,无法进行损伤定位和损伤定量；1/4跨、1/8跨处随着节点数量的增加,支座或损伤处有误导峰值的出现,不能精确定位损伤；由于指标在损伤处的不连续,无法进行定量损伤.综上所述,本例中测点数为33时识别效果最佳.

6 损伤识别实施方案

梁体出现裂缝、受力钢筋锈蚀锈断、局部截面受到车船或漂泊物撞击时,均会导致结构发生损伤,其表征为结构局部刚度的下降.在实际工程中,为了确定损伤的发生,除了对结构外观的普查,刚度的减小从模态特性方面同时表现为较明显的频率下降,可以此作为判断损伤是否发生的依据.确定损伤发生后,采集结构的模态信息,提取一阶竖向振型分量,处理并得到本文提出的指标.同时,提取有限元模型中模拟损伤后不同工况下的模态信息,以此作为训练样本,结合实际结构中的实测振型得到损伤的位置和程度,从而实现损伤定位和损伤定量.具体技术路线如图13所示.

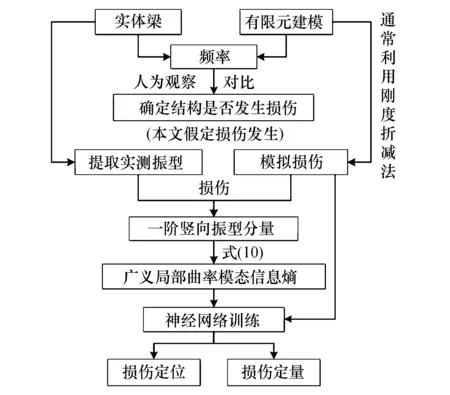
图13 本文识别方法技术路线Fig.13 The technical route for the identification method proposed in this paper

7 结论

通过曲率模态构造广义局部曲率模态信息熵指标,并结合神经网络分别判定一简支梁的损伤位置和损伤程度,最后探讨测点个数与指标精确度之间的关系,结果表明：

1) 广义局部曲率模态信息熵指标和曲率模态指标均可以对弹性范围内简支梁进行损伤位置识别,前者对损伤位置识别的精度略低于后者,但对识别结果没有太大的影响.

2) 与曲率模态指标相同,单独的广义局部曲率模态信息熵指标并不能定量损伤,但其结合神经网络算法可以确定其损伤程度.由于该指标主要呈现“局部”损伤的特性,损伤的位置对其损伤程度的识别效果没有影响,因此具有较好的全局稳定性.在靠近振型节点处,该指标通过神经网络算法对损伤程度的识别结果要优于曲率模态指标.综合结论1),该指标在损伤定位和损伤定量中具有一定的可行性.

3) 广义局部曲率模态信息熵在适当的测点数时能够准确地定位损伤；结合神经网络方法后能够准确识别损伤程度.因此，在实际工程测量中,为了确保损伤位置和损伤程度的准确识别,测点不应布置过于密集.

4) 本文简支梁模型为理想化模型,由于实际工程中存在的不确定性因素,利用本文方法进行损伤识别应进一步进行抗噪性研究和现场试验.此外,现有的损伤识别方法与结构承载力能力评估出现了一定的脱节现象,建立两者的内在联系同样是一个必要的课题.