Mn(c)×R1中具有三个不同特征值的伪平行类空超曲面

戴忠柱, 姜蕴芝, 初裴裴

(营口理工学院 基础部, 辽宁 营口 115014)

众所周知,Lorenzian空间中超曲面的研究在广义相对论中起着很重要的作用.超曲面是余维数为1的子流形,作为子流形的代表得到了广泛研究.1982年,Thurston[1]给出了空间中关于几何化猜想的八个模型以来,许多数学工作者对与该结论相关的乘积空间中子流形问题进行了深入研究,并将其推广到Lorenzian乘积空间中的超曲面问题,关于刻画Lorenzian乘积空间中超曲面的相关几何问题,近几年逐渐成为一个活跃的研究课题之一,见文献[2-3].

伪平行超曲面是半平行超曲面的自然推广,是几何弦理论的模型空间,因此刻画伪平行超曲面的特征具有一定意义.对于空间形式及黎曼乘积空间中的伪平行超曲面的分类已经得到许多深刻的结果[4].关于伪黎曼空间形式中伪平行超曲面还没有完全分类结果,但也得到了许多深刻的结论,Magid[5]研究了Lorenzian空间中平行及半平行超曲面并给出了相应的分类结果,刘建成等[6]研究伪黎曼空间形式中伪平行类空子流形,将黎曼空间形式中伪平行,半平行概念推广到伪黎曼空间形式中,刻画了伪平行超曲面的存在性及几何特征.类比黎曼乘积空间中研究伪平行超曲面的方法,本文研究高维Lorenzian乘积空间Mn(c)×R1中伪平行超曲面存在的充要条件及基本的结论.

1 预备知识

设Mn(c)×R1是Lorenzian乘积空间,其度量为〈,〉=〈,〉Mn-dt2.其中Mn(c)是n维单连通黎曼流形,具有诱导度量〈,〉Mn.光滑浸入f:Σn→Mn(c)×R1是类空超曲面,记

为外围空间Mn(c)×R1的单位类时向量场.对于任意η∈T⊥Σn,T∈TΣn

∂t=f*T+〈η,∂t〉η=T+〈η,∂t〉η

假设η和∂t具有相同的时间定向

其中:θ是η与∂t所成的双曲角.

式中:X,Y∈TΣn,A：TΣn→TΣn为Σn限制到高斯映照N上的形状算子或第二基本形式.

Σn上的曲率算子R定义为

R(X,Y)Z=[X,Y]Z-[X,Y]Z

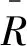
(3)

式中：X,Y,Z∈T(Mn(c)×R1),X*为X在Mn(c)上的投影,且X*=X+〈X,∂t〉∂t，ε=±1.

Gauss方程和Codazzi方程分别为

式中：X,Y,Z∈TΣn；V∈T⊥Σn.

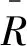
(6)

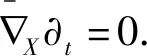
定义1设f:Σn→Mn(c)×R1是等距浸入,若对于任意的X,Y∈TΣn,存在Σn上的实值光滑函数φ,使得

R(X,Y)·B=φ(X∧Y)·B

则称f是伪平行浸入.

若对于任意的X,Y,Z,W∈TΣn,特别地,当φ=0时,f是半平行浸入.由此可见,伪平行浸入是半平行浸入的一个推广.

定义2设H是Σn在Mn(c)×R1中的平均曲率向量场,如果R⊥(X,Y)H=0,则称f是H-平行浸入.

2 主要定理及证明

定理1设f:Σn→Mn(c)×R1是等距浸入,f是伪平行浸入当且仅当

(λj-λi)(c-cε|Tj|2-cε|Ti|2+ελiλj+φ)=0

(9)

或

cεTjTk(λi-λk)=0,(k≠i,j)

(10)

式中:T□=〈T,e□〉,λi,λj,λk是Σn的主曲率.

证明令{e1,e2,…,en}为Σn上局部正交标架场,由伪平行的定义有

另一方面,由Gauss方程(6)及B(ei,ei)=〈Aηei,ei〉η=λiη

将上述两式代入

由伪平行的定义有

φ(λi-λj)=(λj-λi)(c-cε|Tj|2-

cε|Ti|2+ελiλj)η

(λj-λi)(c-cε|Tj|2-cε|Ti|2+ελiλj+φ)=0

同理

R(ei,ej)ek=-εTjTkei+εTiTkej

由伪平行的定义

定理得证.

定理2设f:Σn→Mn(c)×R1是伪平行浸入,则f是H-平行浸入.

证明f:Σn→Mn(c)×R1是伪平行浸入,对任意法向量场η∈T⊥Σn,选取Σn的切标架场{e1,e2,…,en}使得Aηei=λiei,i=1,2,…,n,则对于任意X,Y∈TΣn

另一方面

2〈B(R(X,Y)ei,ei),η〉}=

n〈R⊥(X,Y)H,η〉

结合两式有

R⊥(X,Y)H=0

定理得证.

定理3令f:Σn→Mn(c)×R1是至少具有三个特征值的伪平行类空超曲面,则形状算子Aη有如下表示:

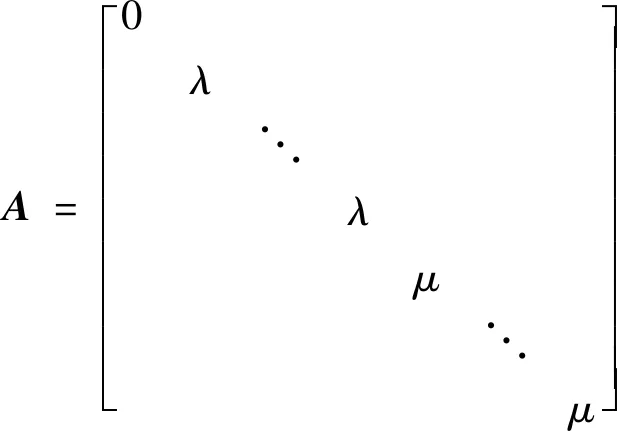
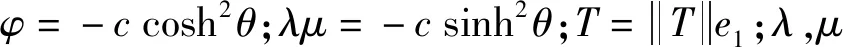
证明令{e1,e2,…,en}为Σn上局部正交标架场,满足:

Aηei=λiei,∀i∈{1,2,…,n}

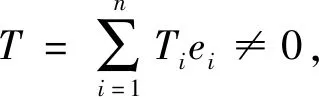
情形1:T∉span{ei,ej},则存在k∈{1,…,n}-{i,j}使得Tk≠0.由方程(10)可知Ti=Tj=0,即T⊥{ei,ej},根据方程(9)得到λiλj=c+φ;

情形2:T∈span{ei,ej},根据方程(11)得到λiλj=ccosh2θ+φ;

由以上讨论,假设Aη的三个特征值为ν,μ,λ,对应特征向量的下标组成的集合分别记为A,B,C.则λμ,λν,νμ∈{c+φ,ccosh2θ+φ},说明三个乘积之间至少有两个相等,不妨假设λν=μν,若ν≠0,则λ=μ,与假设至少有三个特征值矛盾,于是令ν=0,即λν=μν=0,λμ≠0∈{c+φ,ccosh2θ+φ}.

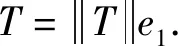
2) 当c+φ=0时,λμ=μν=0=c+φ,由情形1,T⊥span{ei,ej},∀j∈B∪C,∀i∈A,说明T=0与假设矛盾.即λμ=-csinh2θ.定理得证.

说明:由定理3可知,φ=-ccosh2θ≠0对于Lorentzian乘积空间Mn(c)×R1中具有三个不同主曲率的类空超曲面,不可能是半平行类空超曲面.

推论1令f:Σn→Mn(c)×R1是至少具有三个特征值的为平行类空超曲面,则Σn是常角超曲面.

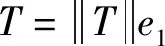
X(coshθ)=-〈AηX,T〉=0

说明coshθ是常数.