储能用多孔铝硅酸盐陶瓷基热物性的研究*

2021-03-08官云许杨启容何卓亚王力伟

功能材料 2021年2期

官云许，杨启容，何卓亚，刘亭，王力伟，赵康

(青岛大学机电工程学院，山东青岛 266000)

0 引言

热能储存(TES)作为一种被广泛研究的技术，具有无穷的潜力，可以通过提高效率来促进可再生能源、化石燃料和核能发电的高效利用，同时使电网兼容性更高。例如，热能储存可以用于集中式太阳能发电(CSP)、核能发电、化石燃料系统发电、地热发电以及风力涡轮机发电在峰值水平运行期间储存过剩能源，减少能源浪费[1-5]。热能储存分为潜热储能[6]和显热储能[7]两种形式，其中潜热储能因其具有较高的储能密度[8]，是最可取的储能方法，在相变过程中温度保持不变，以潜热的形式将能量储存在相变材料中[9]。目前国内外集中式太阳能发电站用来储热的相变材料多为熔融盐中的混合硝酸盐，主要为Hitec熔盐和Solar Salt熔盐[10]。其中Hitec熔盐具有相对较低的熔点，其工作温度为142～535 ℃，熔点为147.2 ℃，分解温度为534.2 ℃，融化潜热为81.14 J/g，平均热导率为0.625 W/(m·K)[11]，其导热率虽然比Solar Salt熔盐导热率0.55 W/(m·K)要高一些，但是相比于单组分硝酸盐和其他相变材料导热率还是较低，在使用时易产生局部过热，因此许多人开始采用各种方法来提高Hitec、Solar Salt等熔盐的导热率和其它热物性。王义豪等[12]采用水法技术制备了熔盐纳米复合材料，研究不同颗粒直径、不同添加量的TiO2对Hitec熔盐比热、导热系数和热稳定性的影响；发现25 nm粒径添加质量分数为0.0625%的TiO2对Hitec熔盐的比热容和导热系数增强效果最佳。武延泽等[13]使用了纳米金属粒子、纳米金属氧化物、纳米碳材料和其他无机纳米材料作为添加剂掺杂到硝酸熔盐体系中进行改性研究。

由于相变材料在相变过程中需要发生相态的变化(一般由固体转换为流体)，造成这些纳米高导热材料添加到融盐中形成的改性相变材料性能不稳定，容易使纳米高导热材料团聚造成改性失败，同时相变材料还存在易泄露、易挥发等问题。为此一些人采用高孔隙的多孔陶瓷[14-15]作为基体来吸附相变材料以制备复合相变储能材料[16]，既达对相变材料改性的目的，又可以对其进行封装。Chuan等[17]以混合碳酸盐作为相变材料、MgO作为陶瓷骨架材料和石墨片为导热增强材料通过混合压片、烧制以制备复合相变材料，并通过对比实验来研究石墨片对复合相变储能材料的导热性影响，当石墨含量达到20%，总体导热率可达到5 W/(m·K)，相较于未添加前的导热率有很大提升。

Lao等[18]采用SiCW/Al2O3蜂窝陶瓷作为显热封装材料，将Al-Si合金(潜热材料)封装在蜂窝孔中，得到具有高温太阳能蓄热能力的合金/陶瓷复合材料；陶瓷孔隙率为51.86%，陶瓷比热容随着温度升高而增大，其中六角孔SiCW/Al2O3蜂窝陶瓷[19]导热率在室温下最高为8.96 W/(m·K)。Feng等[20]综述了纳米孔ssPCMs(形状稳定的PCMs)的研究现状，从制备、结构和热性能等方面进行了综合分析，并对提高纳米孔ssPCMs的热性能提出了解决方案。同时通过总结多孔结构分子动力学(MD)建模来获取直接影响吸附剂-吸附质相互作用的可控参数。

除了上述几种封装材料外，铝硅酸盐陶瓷也是一种很好的封装材料，铝硅酸盐陶瓷[21]是在二氧化硅(SiO2)中加入氧化铝(Al2O3)、氢氧化铝粉(Al(OH)3)混合烧结而成，有的还需要加入氧化钙(CaO)、氧化镁(MgO)等其他材料。因其烧结的温度和材料比例不同会有各种各样的用途，可用作耐火材料、高温工程材料、电子封装材料和光学材料等[22]。且它具有膨胀均匀、热震稳定性极好、荷重软化点高、高温蠕变值小、硬度大、抗化学腐蚀性好等特点[23]，若将其制作成具有定向孔[24]的多孔材料，会较高的导热性能，因而是一种性能优良的封装材料。

综上，复合相变储能材料可以解决相变材料泄露、改性失败等问题，但是在制备复合相变储能材料过程中还存在着骨架材料导热率低、比热容小、孔隙率低等各种物性问题。针对骨架材料存在的这些物性问题，本文采用实验和分子动力学模拟相结合的方法，对多孔铝硅酸盐陶瓷作为复合相变储能材料的骨架材料进行研究。先以刚玉粉(Al2O3)和硅藻土(SiO2)为原材料，通过高温烧结得到多孔铝硅酸盐陶瓷封装材料，并观察其内部结构特征，以期用于吸附Hitec融盐来制备CPCMs。

接着使用Materials Studio(MS)软件建立储能用多孔铝硅酸盐陶瓷基模型，并计算其热物性参数。考虑到多孔铝硅酸盐陶瓷模型中SiO2：Al2O3分子比例不同可能会使陶瓷定压比热容、密度、导热系数以及孔隙率和比表面积等物性发生变化，采用SiO2：Al2O3分子比例为3∶1、2∶1、3∶2、1∶1、2∶3、1∶2、1∶3来建立模型以研究分子比例不同对储能用多孔铝硅酸盐陶瓷基的影响。同时将实验制得的陶瓷材料使用场发射扫描电子显微镜(场发射扫描电镜、SEM)观察其结构变化，研究刚玉粉和硅藻土比例对多孔铝硅酸盐陶瓷基结构的影响。

1 模拟

1.1 模型建立

多孔铝硅酸盐陶瓷的模型基体为Al2O3和SiO2单晶胞，两个基体有不同的晶体结构，Al2O3为六角晶体，空间群为R-3C，晶格参数a=b=0.4761 nm、c=1.2996 nm，α=β=90°、γ=120°；SiO2是四方晶体，空间群为P4122，晶格参数a=b=1.2470 nm、c=2.6331 nm，α=β=γ=90°，结构如图1。在MS软件中去对称后运用Amorphous Cell模块的Construction，温度设为300 K来建立模型，加入Al2O3和SiO2构建基体模型。通过适当增减Al2O3和SiO2晶胞数和晶胞内两种分子的数量来建立Al2O3和SiO2不同比例的多孔铝硅酸盐陶瓷模型，模型的大小保持在2 800个原子左右。图2为结构稳定的SiO2∶Al2O3=3∶1多孔铝硅酸盐陶瓷模型。

图1 Al2O3单晶胞(右)和SiO2单晶胞(左)

图2 多孔铝硅酸盐陶瓷

1.2 模拟方法

本文采用的力场为通用力场(UFF)，在UFF力场中，范德瓦尔力是由 Lennard-Jones(L-J)势能来表示，静电相互作用力由原子单极和屏蔽(距离相关)库仑项描述。其公式为

(1)

其中，Xab是不同分子a和b中的原子间的距离，D和R分别是分子中不同原子间的L-J势能的能量参数和尺度参数，单位分别为Kcal/mol和0.1 nm。q是分子中各原子所带的部分电荷,ε0是自由介电常数，e是电荷的单位。下标a、b分别代表不同分子中的原子对。

建成的模型使用Forcite模块的Geometry Optimization任务进行几何优化，算法为Smart，计算力场为UFF，静电相互作用力和范德瓦尔力分别选用Ewald和Atom based。

然后继续使用该模块当中的Dynamic任务，对非键范德瓦尔力采用截断半径法，截断半径小于立方晶格边长的一半，长程静电相互作用力修正则采用Ewald加和法计算，压力设定在0.1 GPa由Berendsen方法控制，温度设定在1 523 K(1250 ℃，与实验烧结温度一致)下由nose方法控制。在等温等压系综(NPT)下，时间步长为1 fs运行100 ps，使体系达到平衡，接着在正则系统(NVT)条件下运算70 ps达到平衡，最后通过分析得到多孔铝硅酸盐陶瓷模型的各种物理性质。

2 SEM观察并分析

扫描电子显微镜[25]是一种观测样品表面形态的大型电子设备，理论依据是电子和物质的相互作用，即用极狭窄的电子束去扫描样品，通过电子束与样品的相互作用产生各种效应，主要是利用二次电子信号成像来观察样品的表面形态。通过观测可以获取被测物体本身的各种物理和化学的信息，比如晶体结构、组成物质、形貌及电子结构等。本文用SEM观察多孔铝硅酸盐陶瓷内部孔隙形貌和分布情况，以分析多孔铝硅酸盐陶瓷模型的分子动力学模拟孔隙结构的优劣。

表1 主要材料纯度及实验仪器信息

本实验将刚玉粉、硅藻土按照质量比为1∶1.799、1∶1.180、1∶0.882、1∶0.591、1∶0.390、1∶0.290、1∶0.191(SiO2∶Al2O3分子比例换算成质量比例)的比例进行配比，加入可溶性淀粉,每组可溶性淀粉占比皆为10%(质量分数)，使用磁力搅拌器混合分散均匀后加入一定比例明胶溶液和柠檬酸溶液分别作为粘结剂和分散剂，使用压片机压制成陶瓷胚体后在80 ℃下干燥并在1 250 ℃下烧制成多孔陶瓷，然后取出部分陶瓷后进行SEM观察，研究其结构变化。

3 结果与分析

3.1 铝硅酸盐陶瓷模型的导热性能

本文主要研究孔铝硅酸盐陶瓷骨架的导热率，故先从多孔铝硅酸盐陶瓷模型上取出没有孔隙的部分铝硅酸盐陶瓷骨架作为此陶瓷模型的测量目标，用反向非平衡动力学(RNEMD)的方法，通过将冷层中最热的粒子和热层中最冷的粒子的动能进行能量交换，强加一个能量通量jz于模型z方向上，待系统达到稳态时，可得到模型z方向上的温度梯度，复合材料的导热系数λ(W/(m·K))可以通过能量通量jz和模型z方向上温度梯度dT/dz进行计算，计算公式为：

(2)

能量通量jz(W/m2)的计算公式为：

(3)

其中，t表示能量交换的时间，A表示能量通量方向上的截面积，m表示参与能量交换的原子的总质量，vh表示模型中热域原子的速度，vc表示模型中冷域原子的速度。

如图3所示随着Al2O3加入比例增加，铝硅酸盐陶瓷的导热率增速较大，且呈现出分段线性增加趋势，在SiO2∶Al2O3分子为1∶1之前增速较慢，之后则增速加快，当SiO2∶Al2O3分子为3∶1和1∶1时导热率分别是2.025 W/(m·K)和4.179 W/(m·K)，而SiO2∶Al2O3分子为1∶3时达到最高值8.34 W/(m·K)，这与其他高导热硅铝酸盐陶瓷的导热率[26-27]相差无几，是混合硝酸盐导热率0.5 ～1.0 W/(m·K)的8～16倍，因而是一种优异的高导热陶瓷骨架材料。

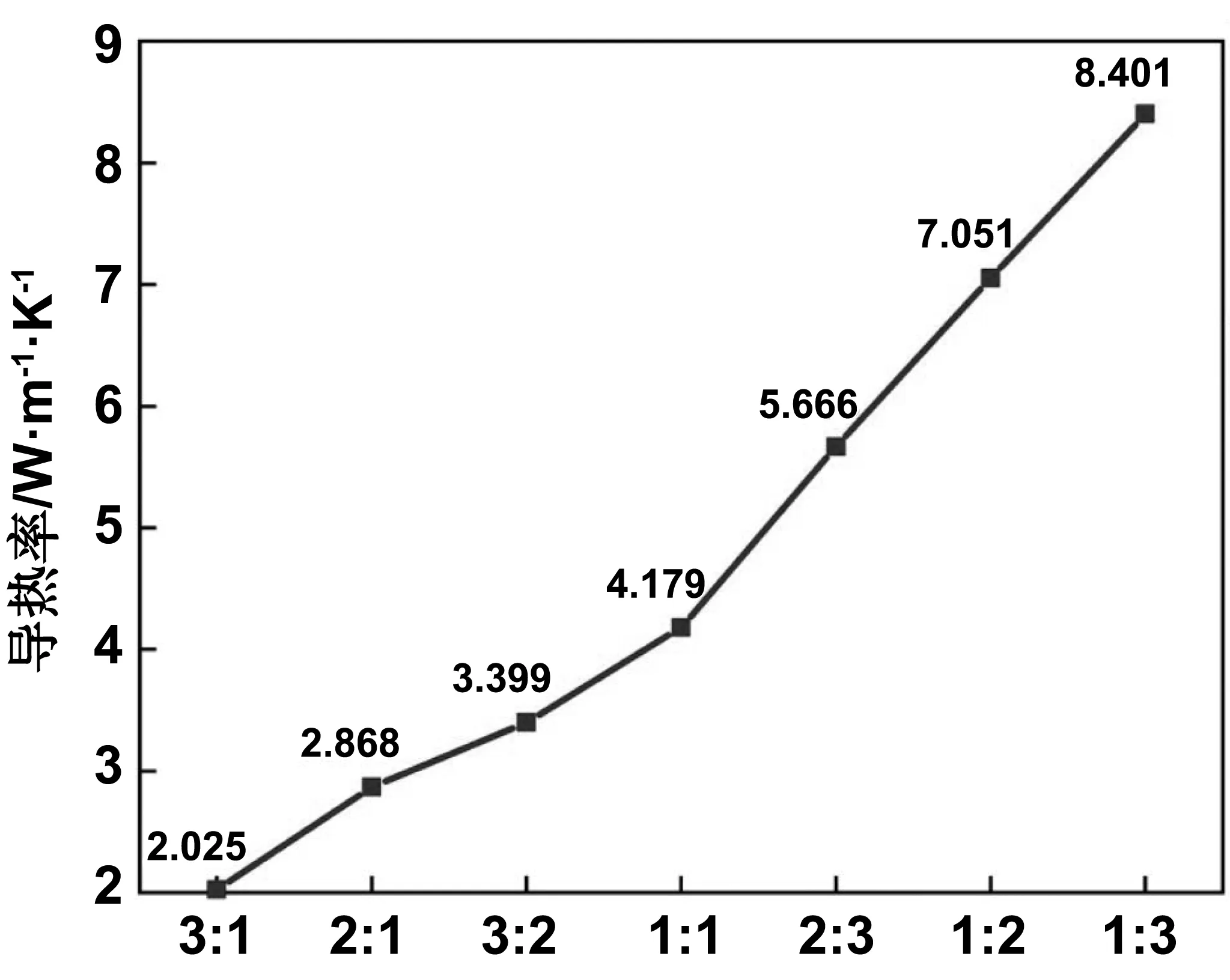
图3 铝硅酸盐陶瓷导热率

3.2 多孔铝硅酸盐陶瓷模型的密度

模型的密度可用以下公式计算：

(4)

其中N是原子数，M是摩尔质量，Vall是模拟盒的平衡体积，NA是Avogadro常数。

多孔陶瓷密度如图4所示，从整体上看多孔陶瓷随着Al2O3添加量增加其密度逐渐变大，由最初的SiO2∶Al2O3分子为3∶1密度为1.38 g·cm-3提升到SiO2∶Al2O3分子为1∶3密度为1.76 g·cm-3，提升速度较为缓慢。

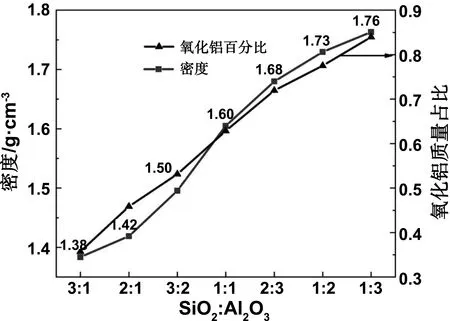
图4 多孔铝硅酸盐陶瓷密度

同时密度增大会影响储热密度，即随着Al2O3添加量增加将导致多孔陶瓷吸附相变材料后形成的CPCMs储热密度下降。

3.3 多孔铝硅酸盐陶瓷模型的定压比热容

计算铝硅酸盐陶瓷定压比热容的方法有两种，一是采用能量波动方式，另一个则是利用焓变来计算热容，这两种方式都要在等温等压系综(NPT)条件下进行计算并达到平衡。本文采用的方法是从能量的波动中计算它热容的变化，其公式为：

(5)

(δE2)=(E2)-(E2)

(6)

E是总能量(势能和动能之和)。kB是Boltzmann常数，T是温度。

对于硅藻土和刚玉粉矿物的定压比热容，需要通过比热容与温度的关系式来计算理论数值，其公式为：

Cp=A1+A2×10-3T+A3×105T-2+A4×10-6T2+A5×108T-3

(7)

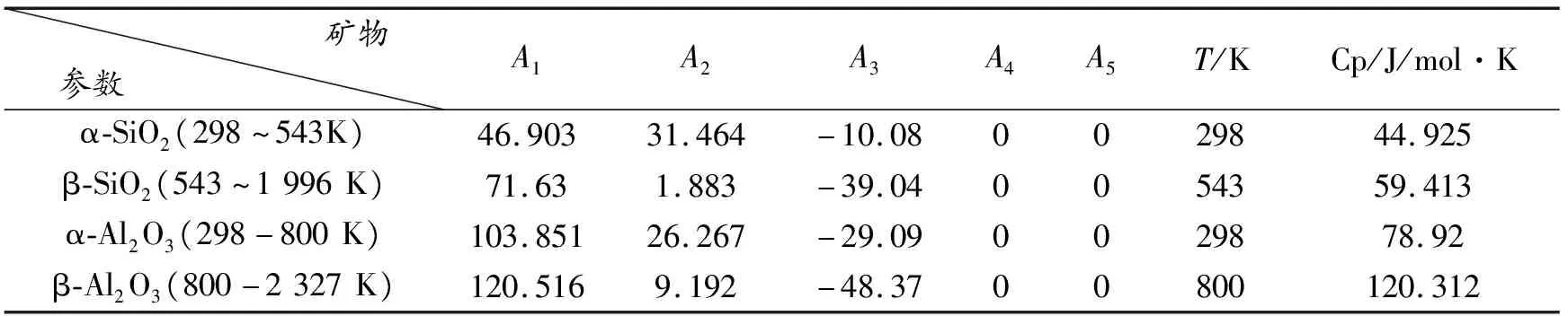
表2 式7中A1～A5的值

图5是在不同温度下多孔铝硅酸盐陶瓷定压比热容的变化，其中最上部曲线和最下部曲线分别是矿盐硅藻土(SiO2)和刚玉粉(Al2O3)的理论定压比热容曲线，图7和是SiO2和Al2O3理论Cp和模拟Cp关系，图8是SiO2和Al2O3理论Cp和模拟Cp关系，可以看出理论和模拟数值基本一致且变化相同，同时从图5可以看出多孔铝硅酸盐陶瓷在相同温度下比例为SiO2∶Al2O3分子为1∶3时Cp最大，在300和900 K时Cp分别为74.81和104.80 J/(mol·K)；在SiO2∶Al2O3分子为3∶1时定压比热容最小，300和900K时分别为57.85和81.72 J/(mol·K)。

图5 不同温度下多孔陶瓷定压比热容

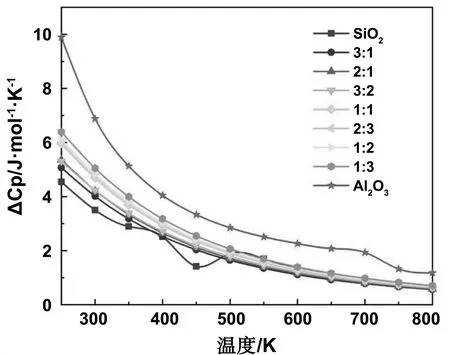
图6 相邻温度多孔陶瓷定压比热容差值

图7 SiO2和Al2O3理论与模拟定压比热容

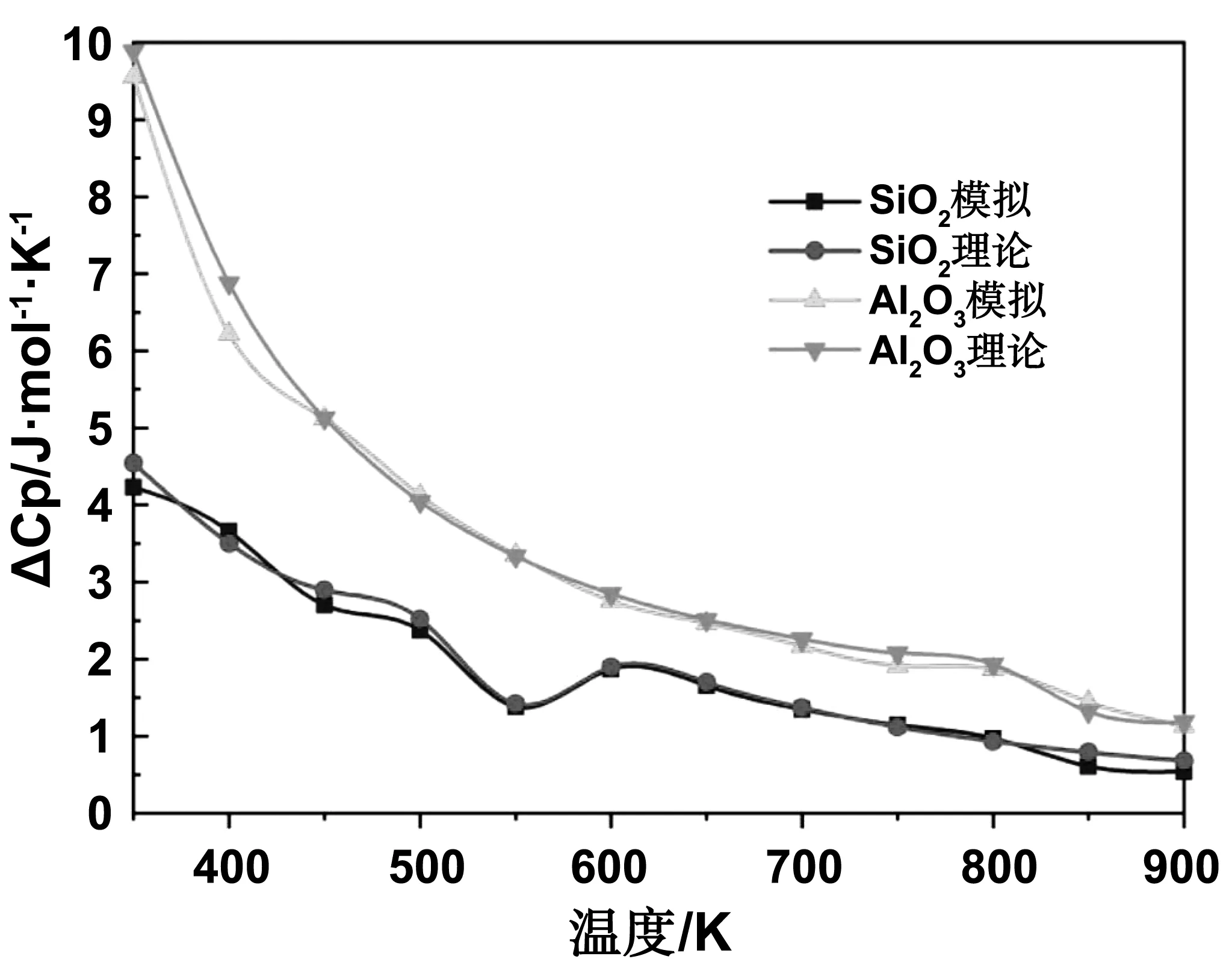
图8 SiO2和Al2O3理论与模拟定压比热容差值

由于Al2O3的定压比热容比SiO2大，多孔铝硅酸盐陶瓷随着Al2O3含量增加，其定压比热容逐渐增加，当Al2O3含量恒定时，多孔铝硅酸盐陶瓷定压比热容随着温度的升高逐渐升高。

由图6知随着温度的升高，无论是理论还是模拟的结果，多孔铝硅酸盐陶瓷Cp逐渐降低且整体上小于Al2O3的Cp，大于SiO2的Cp，结合着孔铝硅酸盐陶瓷定压比热容随着温度的升高逐渐升高这一结论，可知多孔铝硅酸盐的定压比热容及其差值介于 SiO2和Al2O3之间，且定压比热容与Al2O3含量和温度呈正相关，比热容差值与温度呈负相关、与Al2O3含量呈正相关。

3.4 多孔铝硅酸盐陶瓷模型的孔隙率比表面积

多孔材料的孔隙率又被人称之为孔率、孔隙度或者气孔率，指的是多孔材料中孔隙所占的体积与总体积之比，其公式为

(8)

其中Vpore表示单个孔隙的体积，Vall为总体积。孔隙率的多少和孔隙的好坏决定着多孔材料导热性、导电性、力学性能、光学性能等。

比表面积固体物质单位质量所具有的表面积，分为内表面积和外表面积，但是本文中所说的比表面积特指比内表面积。公式表达为

(9)

其中Sin表示内表面积，ρ为材料密度，Vall是总体积。比表面积越高，材料的热学性质、吸附能力、化学稳定性越好；对于多孔铝硅酸盐来说，比表面积越高，吸附的相变材料越多，吸附后稳定性越好，复合相变储能材料的热力学性质越好。想要得到孔隙总体积和内表面积，需要用Atom Volumes&Surfaces工具来创建多孔铝硅酸盐陶瓷内表面，如图9。同时将得到的孔隙总体积和内表面积进行计算得到多孔铝硅酸盐陶瓷孔隙率和比表面积。

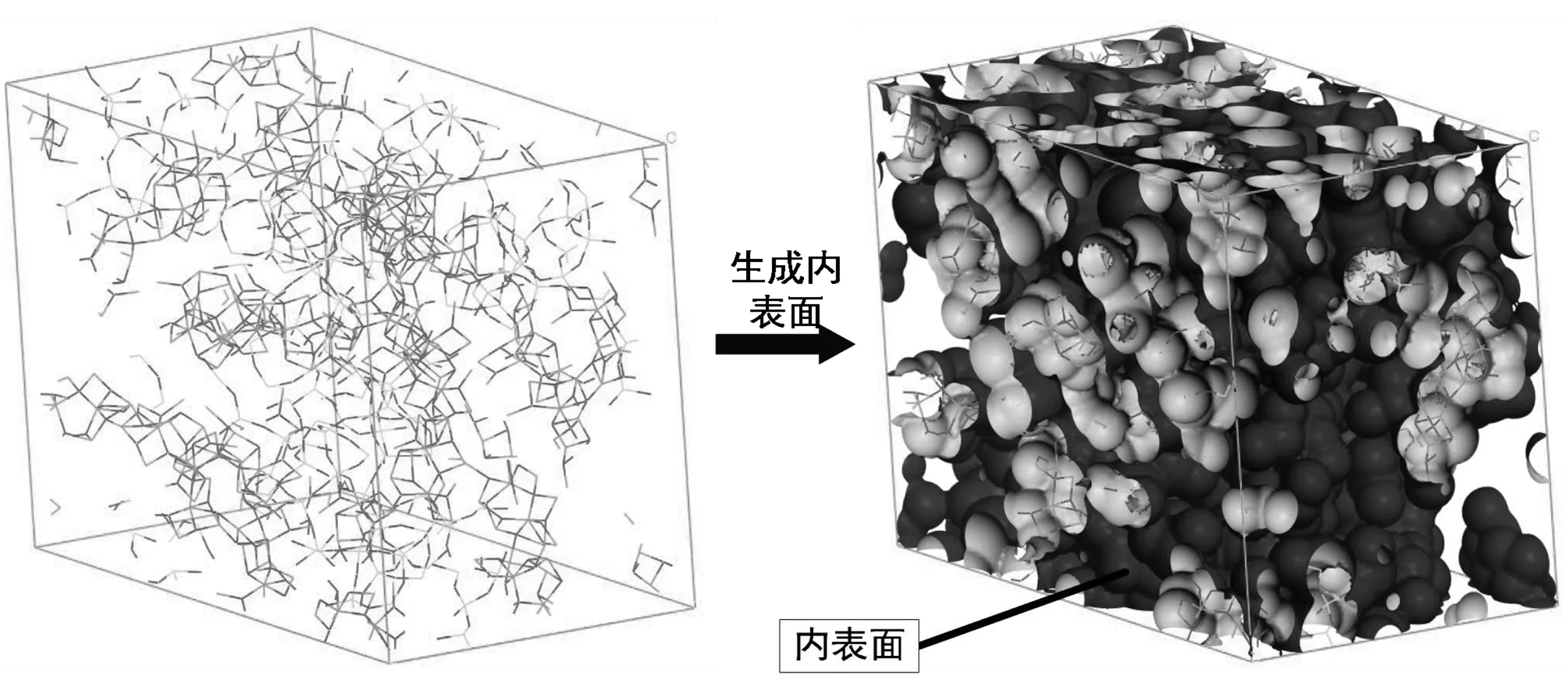
图9 Al2O3∶SiO2=1∶2多孔铝硅酸盐陶瓷创建内表面

如图10所示，在本次模拟研究中多孔铝硅酸盐陶瓷当SiO2∶Al2O3分子为3∶1时孔隙率最小，为42.66%，此时比表面积也是最小，为118.58 m2/g；在SiO2∶Al2O3分子为1∶3时孔隙率为57.42%，此时比表面积为469.81 m2/g。多孔铝硅酸盐陶瓷中SiO2∶Al2O3分子为1∶3相较于SiO2∶Al2O3分子为3∶1，孔隙率提高14.76%，比表面积提高296.20%。实验孔隙率与模拟孔隙率数据变化一致，孔隙率最小为41.60%，最大为56.02%；由图10 可知所有比例下实验孔隙率比模拟孔隙率都要小，这是由于模拟中可把一些闭孔的孔隙计算出来，而实验却无法测量。

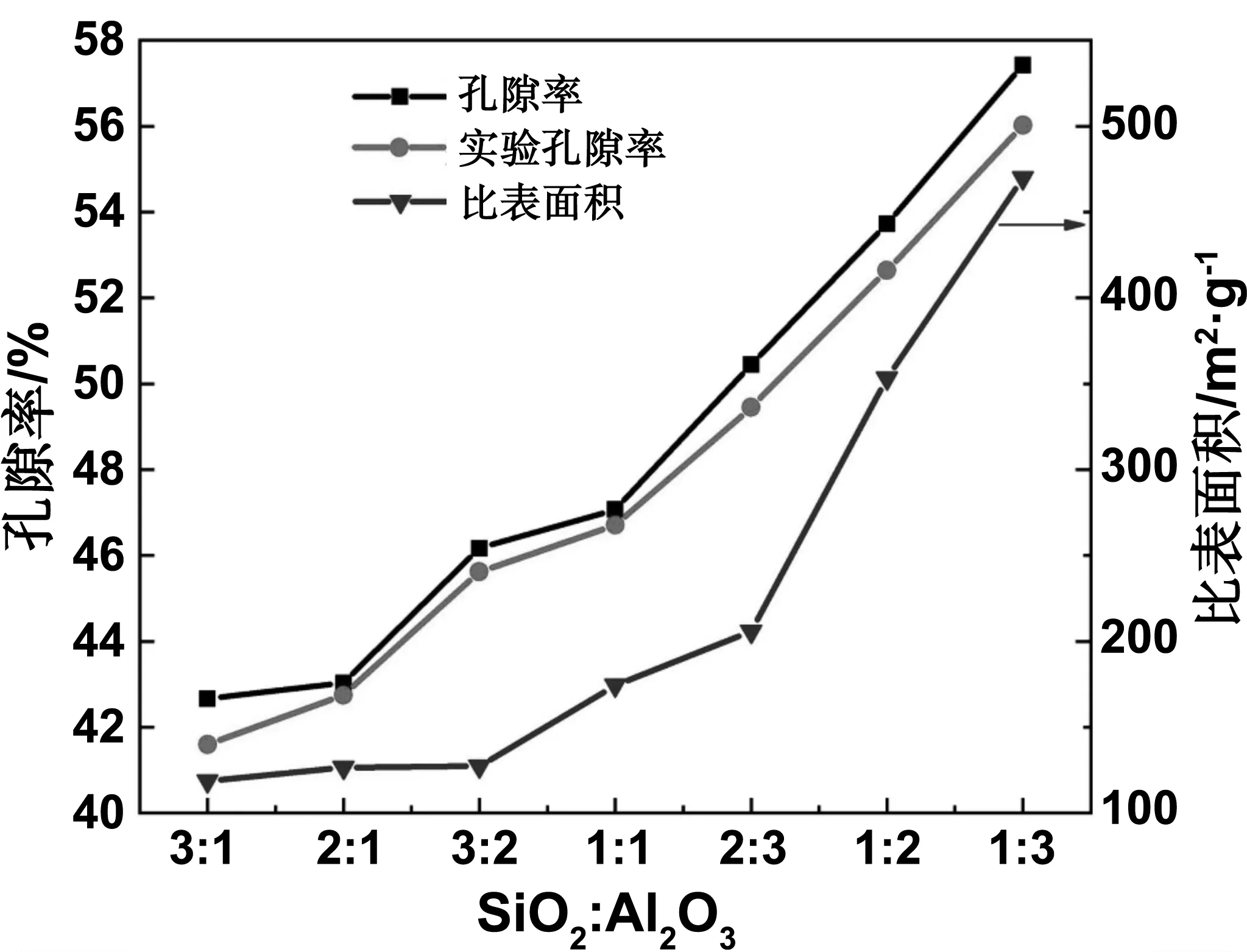
图10 多孔铝硅酸盐陶瓷孔隙率和比表面积

由图4中可以看出氧化铝重量占比总体提升48.23%，而密度总体提升27.54%，而图10模拟孔隙率最大提高14.76%，说明氧化铝占比提升较大，不但可使密度变大，还可以提高陶瓷的孔隙率；同时密度的提升幅度小于氧化铝占比的提升，孔隙率提高幅度小于密度提升幅度。

由图10知多孔铝硅酸盐孔隙率和比表面积的虽然变化趋势是一致的，但是变化幅度不相同，这是由于陶瓷内部孔隙的微孔、中孔、大孔的比例不一样造成的，即孔隙率一定，微孔越多，比表面积越大，反之亦然；而且微孔、中孔、大孔构成三维网状结构[28]，有助于形成有效的传热网络，从而有助于改善吸收Hitec盐后CPCMs的传热效率。

3.5 SEM实验分析

图11中a～g依次是从SiO2∶Al2O3分子为3∶1至SiO2∶Al2O3分子为1∶3比例区间内的多孔铝硅酸盐陶瓷SEM图像，由此可以看出，随着Al2O3的比例逐渐上升，陶瓷结构发生变化:对比图(a～d)中孔隙中间出现较多的颗粒且不规则的粒状结构，从图(e)开始到图(g)其孔隙更加的分散，是分布更加均匀的片状结构[29]，且此片状结构多数都平行于观察的平面，这种片状结构属于多孔铝硅酸盐陶瓷中的定向孔结构的一种，有助于提高多孔铝硅酸盐陶瓷的导热性能[30]，这与前文3.1中导热率在SiO2∶Al2O3分子为1∶1后快速增加的结论相互验证。层层片状结构相比之前的粒状结构在相同体积下比表面积会有很大提高，可以说明多孔铝硅酸盐陶瓷模型中孔隙率和比表面积为何在SiO2∶Al2O3分子为2∶3后的比例快速增加。