便携式机箱内部PCB间微带线的耦合特性分析

吴其霖，谭康伯，路宏敏

(西安电子科技大学 电子工程学院，陕西 西安 710071)

随着便携式机箱内电子系统向着高速度、高密度的趋势发展，机箱内部模块布局越来越紧凑，模块印刷电路板(Printed Circuit Board，PCB)上传输信号的微带线也越来越密集。此时在同一块PCB上甚至相邻PCB上微带线间存在复杂的电磁耦合，将对设备的工作性能产生极大的负面影响[1-5]。因此研究机箱内微带线间的耦合特性对解决机箱内部EMC问题有重要的贡献作用。

文献[6]通过HFSS仿真软件仿真和实物测试对两条无关的微带线之间串扰问题进行了研究，分析了受扰线近端、远端串扰强度在不同频率远端串扰强度以及在不同频率、间距、线长、反射条件下的分布特性。文献[7]以某DDR4驱动模型和板级嵌入式应用为研究对象， 建立多线打扰模型， 从时域角度仿真分析布线间距、打扰源相位、数据速率、耦合传输线长对带状线传输串扰的影响。文献[8]对平行平面曲折传输线的串扰降低进行了详细研究和分析。讨论了不同弯曲角度的微带线的传输特性，反射特性和串扰特性，以了解PCB设计中的串扰设计。上述文献对同一块PCB上微带线间的串扰问题进行了较为详细的研究，但是对于同一个设备机箱内的不同子系统中不同PCB上的微带线之间的耦合、辐射等高频效应涉及较少。本文将通过对机箱、PCB和信号的电磁建模，研究在设备机箱内不同PCB上微带线之间的电磁耦合特性。

1 理论分析和模型建立

在微带贴片表面存在着微带电流产生的切向散射电磁场Es和入射电磁场Ei(激励场)。外部入射电磁场会在传输线导体上感应出电流和电荷。由于电磁之间的相互关系，这些电流和电荷又会形成散射场，感应的散射电磁场和入射电磁场共同满足传输线导体表面的边界条件。基于电磁场理论[9-10]，在微带贴片的表面存在含电流面密度J的方程

Es+Et=ZsJs(ρ)

(1)

其中，Zs是微带结构的表面阻抗，决定了微带贴片的欧姆损耗。贴片是理想导体的情况下，可以得出如下结论

Es=-Et

(2)

根据麦克斯韦旋度方程[11]，可得下列等式

Es=-jωA-φ

(3)

其中，

A(r)=∬SGA(r，r′)J(r′)dr′

(4)

φ(r)=∬Gq(r，r′)qs(r′)dr′

(5)

且J和qs满足连续性方程×J=-jωqs，GA是空域矢量位并矢格林函数，Gq是空域标量位格林函数。 切向电场分量则可表示为

(6)

(7)

其中，“*”表示空域卷积；J是导电贴片上的表面电流密度。由式(2)～式(5)可知Z=0上的切向场量

(8)

(9)

由此可计算微带线的辐射电磁场以及耦合电压。

本文所研究的某型号机箱如图1所示，其外壳为铝合金材质，在外壳上开有大面积的散热孔，在箱体内部中间横置着背板，该背板为便携式设备模块间信号交换的总通路。本文所研究的微带线位于该背板以及工作时插入使用的模块上。

图1 某型号机箱实物图

实际建模后模型如图2所示。

图2 某型号机箱模型图

使用该精细模型计算可以获得较为精确的结果，但是由于微小结构众多，必然会导致电磁仿真模型网格数目急剧增多，使模型变得复杂，造成计算量的增加，占用极大的计算资源[12]，甚至由于计算机资源的限制而无法完成仿真分析工作。为了兼顾计算结果的准确性和计算能力，根据微绕理论[13-15]，对屏蔽机箱谐振频率和场强分布没有影响的零件结构，本研究采用零件类型的模型简化方法进行处理。针对机箱壁金属微扰，本文则提出了基于电磁微扰理论的模型简化方法，并给出了屏蔽体内受介质微扰时微小介质材料可以忽略的条件，如式(9)所示。

(9)

其中，E1、H1为受扰动后屏蔽体内的电场和磁场；εr1为微扰介质材料的介电常数；ε0和μ0分别为空气的介电常数和磁导率；W0为屏蔽体内部空间存储的总电磁能；ξ为误差常数，工程中常取0<ξ<0.01。此外，实际工作中机箱前部还会加上防护片。综上所述，化简后的模型如图3所示。

图3 化简后某型号机箱模型图

由傅里叶变换可知，时域中周期性的信号仅有谐波频率成分。也就是在其频谱中，仅在周期信号频率整数倍的频率处有成分，其他频率没有任何频谱成分，这种频谱称为离散的。而时域中非周期性的信号，其频谱成分分布在所有频率上，这种频谱称为连续的。时钟信号是一种周期信号，它的能量主要集中在某些频点上，造成的辐射干扰也相对更强，是PCB上主要的干扰源之一[16]。因此本文主要研究时钟信号造成的干扰。

该机箱所使用的时钟信号是一个周期为10 ns，电压幅值为3.3 V，上升下降时延为0.6 ns的信号。其时域波形和频域频谱分别如图4和图5所示。

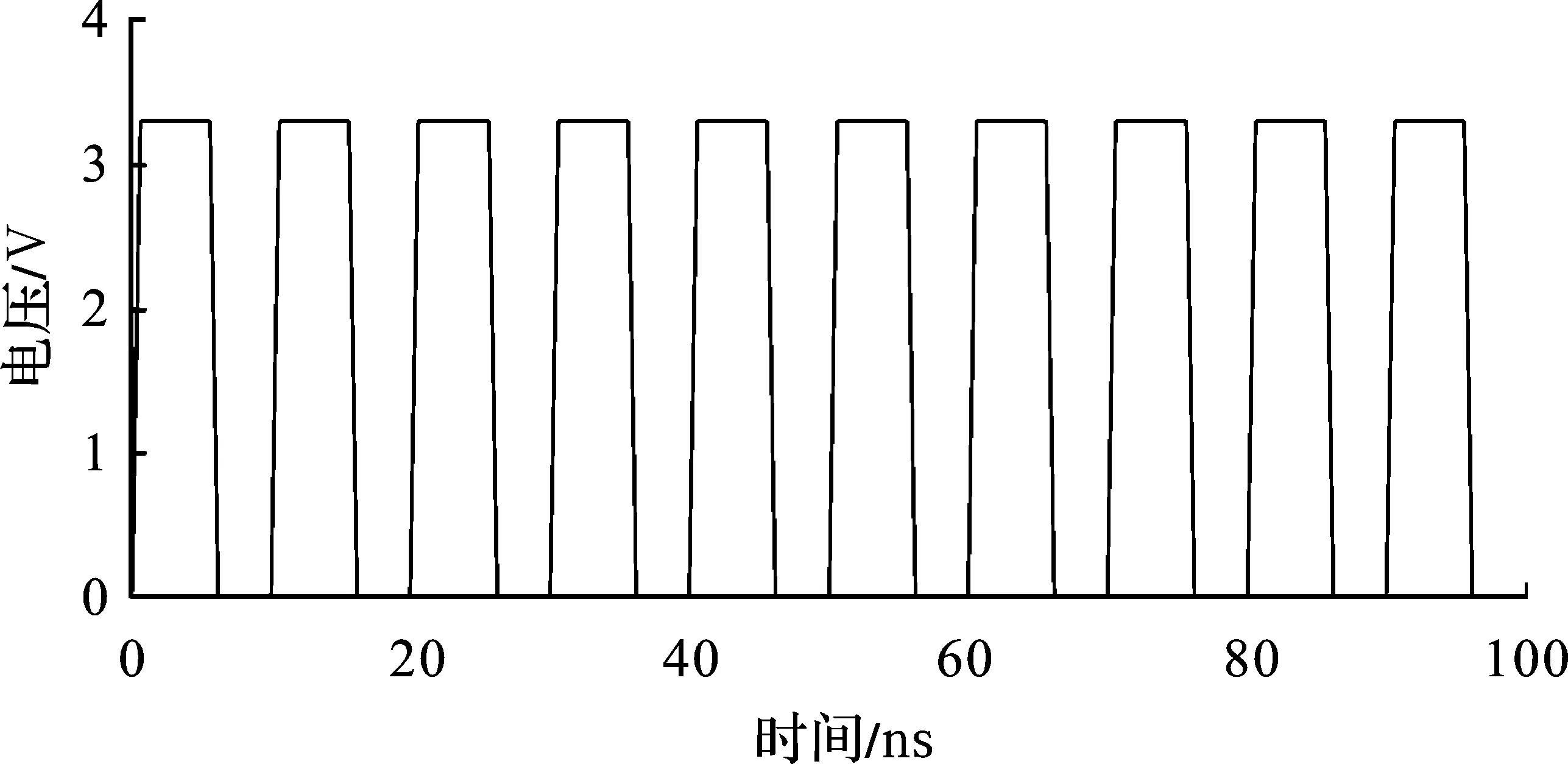
图4 时钟信号

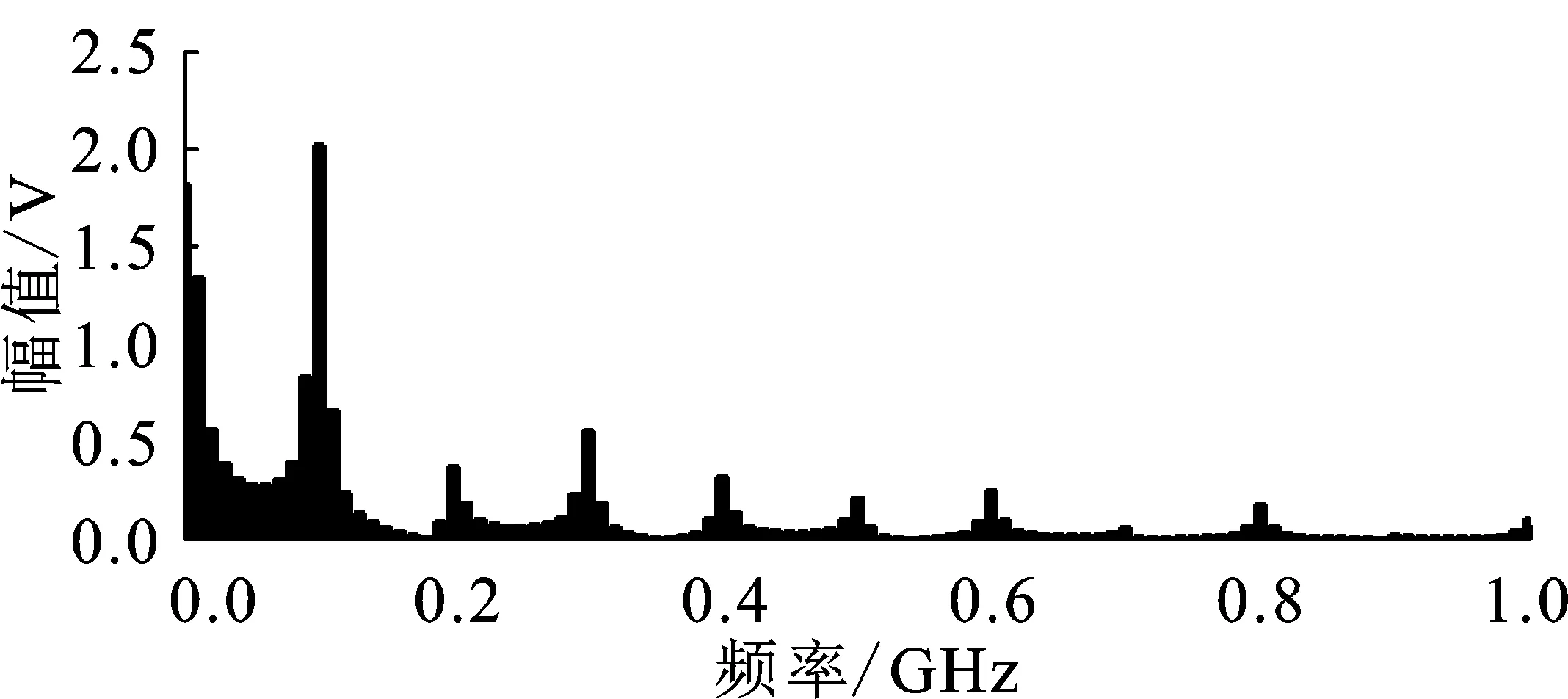
图5 时钟信号频谱

2 仿真分析

本文研究的微带线介质层为FR4，相对介电常数εr=4.4，厚度h=0.8 mm，微带线宽w=1.5 mm，长度l=112 mm，特征阻抗为50 Ω。其一端接50 Ω匹配负载，一端接时钟信号，模式如图6所示。

图6 时钟信号线模型

在该微带线上方3 mm处的电场和磁场辐射分别如图7和图8所示。

图7 电场辐射强度，峰值为780 V·m-1

图8 磁场辐射强度，峰值为1.6 A·m-1

其电场和磁场辐射强度较大区域均在微带线附近，因此空间位置与时钟信号线靠近的微带线需要优先考虑，特别是和时钟信号线平行的微带线耦合情况。

根据该设备机箱内部实际工作情况，背板位于机箱中部，各模块垂直背板插入机箱使用，其中控制器模块位于两块垂直背板的平行PCB中左侧部分。本文研究中的时钟信号线也位于该部分，其他PCB上的微带线考虑空间位置最接近时钟信号线的部分。各模块和背板之间PCB的相对位置及微带线如图9所示。

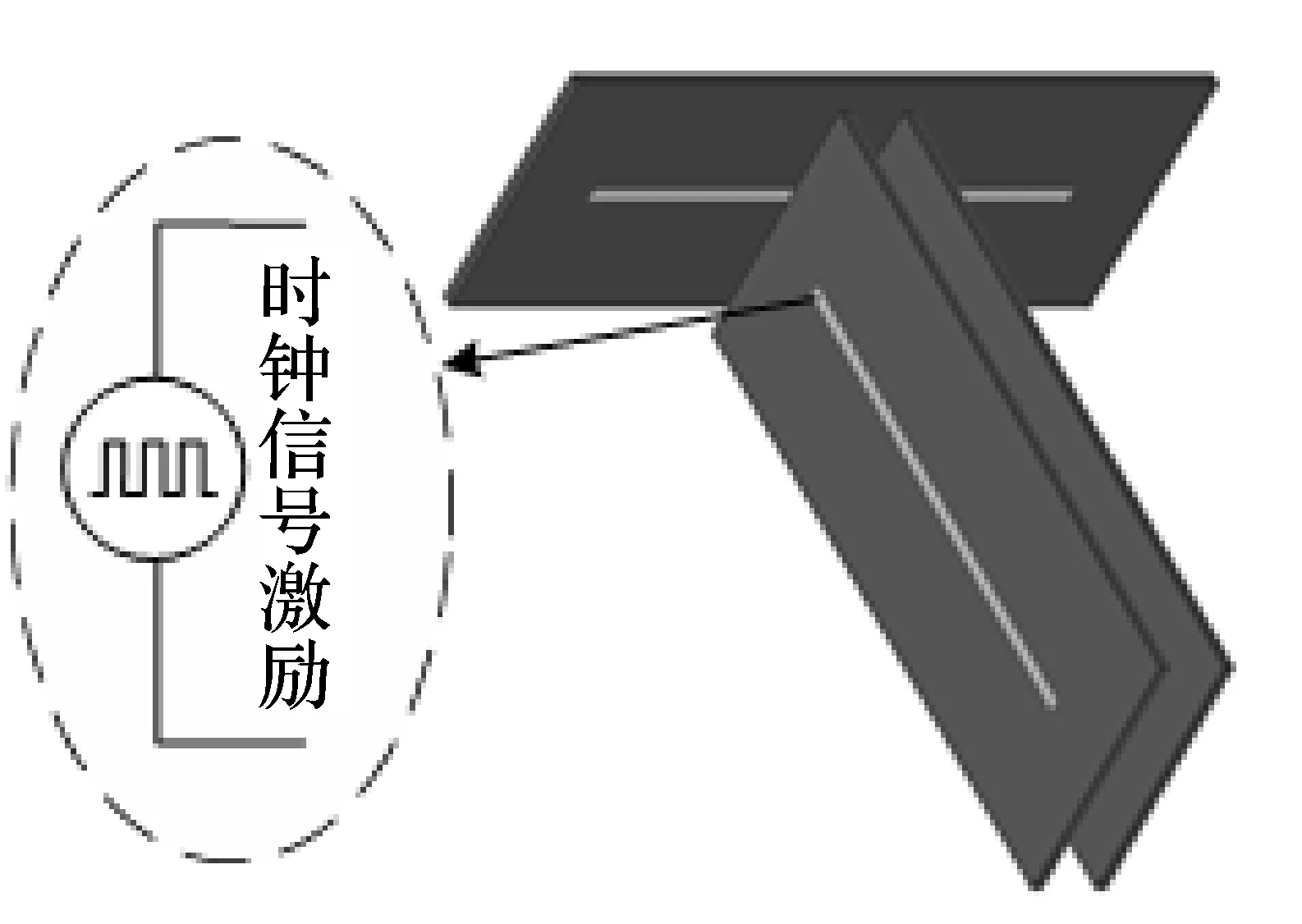
图9 PCB相对空间位置

首先将其置于自由空间中，与时钟信号所在PCB平行和垂直的PCB上微带线的耦合电压分别如图10和图11所示。

图10 平行PCB上微带线的耦合电压

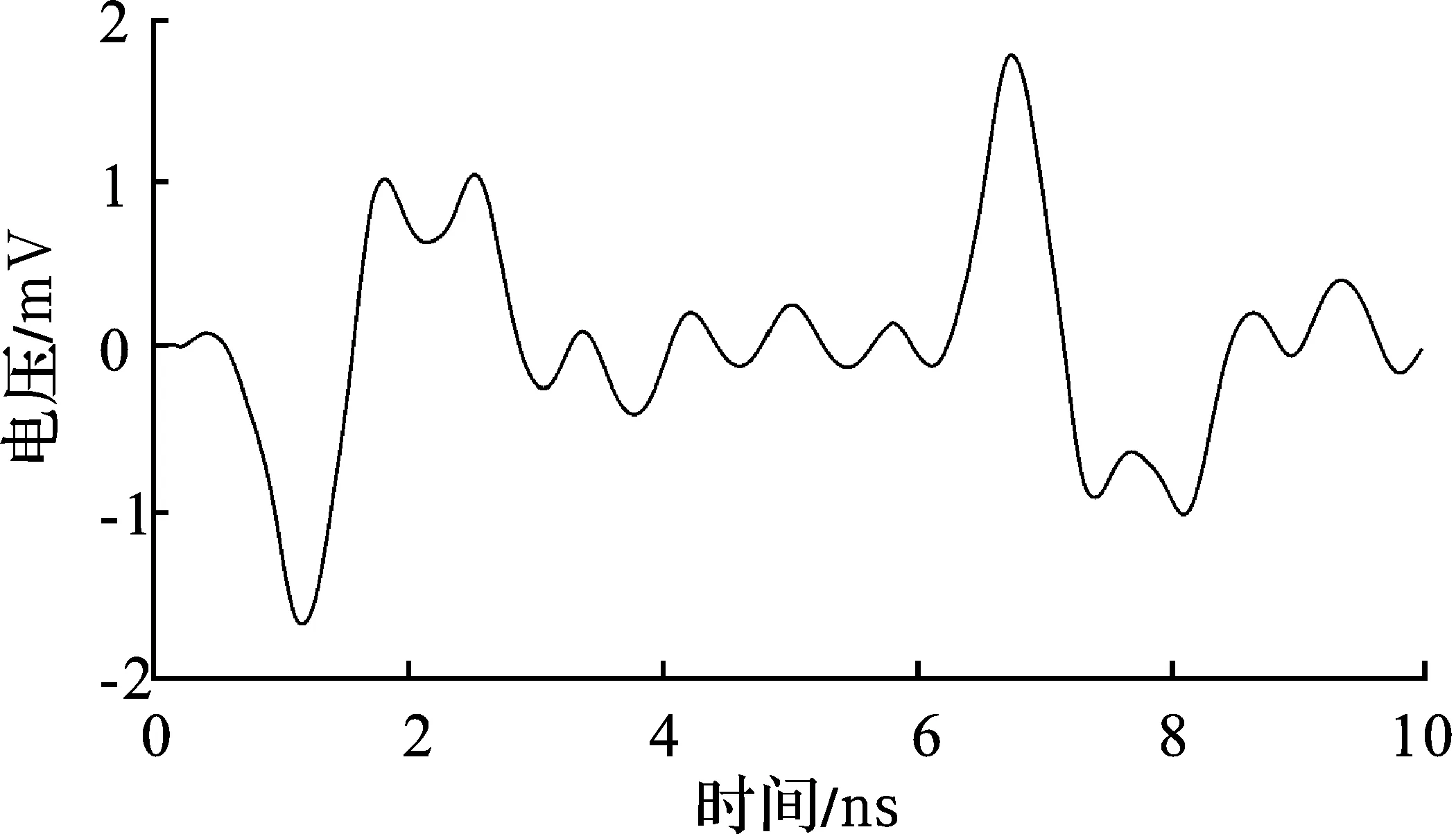
图11 垂直PCB上微带线的耦合电压

由图10和图11可知，平行PCB微带线上的耦合电压和垂直PCB上微带线的耦合电压峰值几乎一致，约为1.8 mV。平行PCB微带线上的耦合电压起伏情况与时钟信号的上升下降沿一致。在时钟信号上升时，平行PCB微带线上的耦合电压出现并快速达到峰值；在时钟信号幅值为3.3 V时，耦合电压相对较为缓慢地下降，并伴随较小的起伏，直到0 mV。垂直PCB微带线上的耦合电压起伏情况与时钟信号的上升下降沿相反，并且在时钟信号幅值为3.3 V时，快速上升到1 mV，随后再次下降到0 mV附近，也伴随着较小的电压波动。上述结果表明，平行PCB上微带线的耦合电压响应趋势与时钟信号上升下降沿紧密相关，呈正相关关系，垂直PCB上微带线的耦合电压响应趋势呈负相关，且在达到峰值之后，下降时会产生类似过冲的现象，最后电压才在0 mV附近波动。

将上述PCB置于简化后的箱体内部，示意图如图12所示。

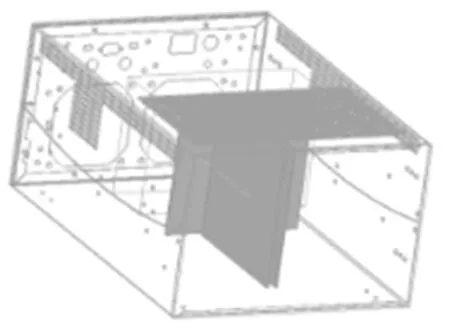
图12 PCB置于箱体内部

其与时钟信号所在PCB是平行和垂直关系的PCB上微带线的耦合电压分别如图13和图14所示。

图13 平行PCB上微带线的耦合电压

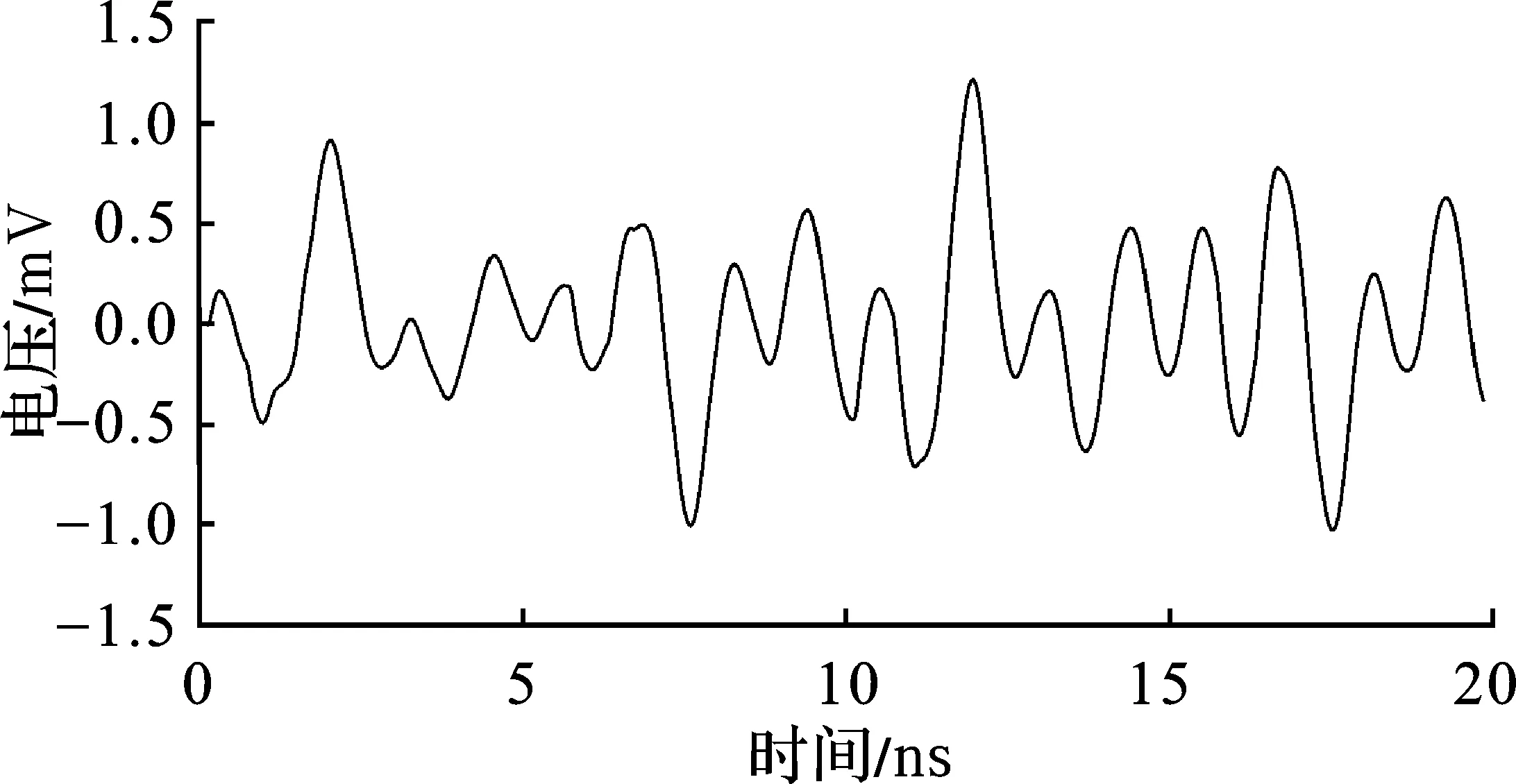
图14 垂直PCB上微带线的耦合电压

由图13图14可知，此时平行PCB微带线上的耦合电压的峰值要小于垂直PCB上微带线的耦合电压峰值，且都比在自由空间中的小，说明在机箱内平行PCB微带线上的耦合电压受到的抑制影响较大。平行PCB微带线的耦合电压整体起伏趋势仍和在自由空间中的保持一致，但是其电压波动较为剧烈。垂直PCB微带线仍有比较明显的在一个时钟上升或下降沿时，耦合电压出现一次波谷和波峰，最后在0 mV附近波动的情况。但是相较于自由空间的耦合电压波形，其波谷电压降低程度要大于波峰电压，以至于由自由空间中的大于关系变成了小于关系。

综上可知，与时钟信号线所在PCB平行的PCB上微带线的耦合电压峰值在自由空间时为1.8 mV，在机箱内峰值有明显的下降，约为0.5 mV。另外在机箱内和在自由空间时，耦合电压整体的起伏趋势都和时钟信号上升沿和下降沿呈正相关，只是在机箱内耦合电压曲线波动更加激烈。而与时钟信号线所在PCB垂直的PCB上微带线的耦合电压峰值在自由空间时也约为1.8 mV。但在机箱内的耦合电压峰值为1.25 mV，下降幅度要小于平行的情况。另外耦合电压整体的起伏趋势虽然都和时钟信号上升沿和下降沿有关，但是在时钟信号的上升沿时，耦合电压先是出现负的峰值，然后迅速上升为正的峰值，下降沿时反之。无论何种情况，在时钟信号的上升和下降沿，耦合电压的变化是最大的。在箱体内部时，整体的耦合电压都有明显下降，且耦合电压整体的波动性变得更加剧烈，比时钟信号线所在PCB平行的微带线耦合电压的下降程度更大。所以在这种情况下，垂直PCB上的微带线耦合电压情况更值得关注。

3 结束语

本文对机箱内不同PCB上的微带线之间的耦合特性进行了研究，得到了在机箱内和在自由空间中与时钟信号线所在PCB平行或者垂直的PCB上微带线的电压耦合特性。在机箱内部设计系统时，各模块的相对距离应尽可能地远以减小耦合；在有限空间内，PCB间的空间位置应优先考虑平行布置；对于时钟信号，其位置应尽量远离其他容易受扰的微带线，或采取屏蔽手段以提高机箱的整体电磁兼容性。