一类不稳定时滞对象的两自由度控制器设计

朱景秀，张 伟，王亚刚

(上海理工大学 光电信息与计算机工程学院，上海 200093)

在实际生活中，不稳定系统和积分系统的调节技术要比稳定系统复杂和困难得多，在加上时延后，研究难度更高。近几年，为了稳定时滞不稳定系统，研究人员将重点放在了PID(Proportional-Integral-Derivative)控制器的设计上[1-9]。文献[1]针对一类二阶不稳定系统，提出了一种改进史密斯预测器的设计方案。该方案基于直接综合法将设定值追踪控制器和扰动控制器分别设计为PID形式和带超前滞后滤波器的PID形式，并且加入设定值加权来减小超调。文献[2]提出了一种直接综合法来设计积分系统的PID控制器参数，其整定方法基于特征方程与期望方程的比较。文献[3]提出了一种并行控制结构(Parallel Cascade Control Structure，PCCS)，该结构特点是将设定值追踪响应和抑制扰动响应解耦，可以更加灵活地提高系统性能。一阶不稳定系统的稳定方法如下：文献[4]提出双倍两自由度(Two Degree of Freedom，2DOF)的内模控制(Internal Model Control，IMC)结构，该结构实现了系统性能的提高。但是其控制器的数目众多，参数设计复杂并且未能给出系统的调参规则。文献[5]将直接综合法和帕德(Pade)近似法相结合来分析调优规则的表达式，该设计方法简单，但是系统响应的超调量大。文献[6～7]均提出两自由度结构的改进方案，控制器的设计方案都是先处理不稳定过程，再分别设计设定值追踪控制器和扰动控制器。文献[8]针对一阶不稳定系统提出一种两自由度解析方案。文献[9]提出一种对PID控制器进行参数优化的改进算法。该算法的优点是提高了参数整定精度，但其缺点是计算量大、过程复杂，且不能普遍应用于工业和化学工厂中。由以上文献可以看出，虽然经典PID的研究已很成熟，但是系统响应超调量大，不能在提高系统性能的同时提高鲁棒稳定性。因此，不稳定系统的系统性能以及鲁棒稳定性仍然有提高的空间。

本文结合原方案[6]的两自由度结构提出一种控制器的改进方案。该方案是利用该结构能将设定值追踪响应和抑制扰动响应解耦的结构特点，将控制器分开设计，其中设定值追踪控制器和稳定不稳定过程的控制器分别选用比例积分(Proportional Integral)和比例(Proportional)的控制器形式，扰动控制器选用带超前滞后滤波器的PID控制器形式[10-15]。本文算法是保持原方案中设定值追踪响应的控制器设计方案不变，基于直接综合法得到扰动控制器的解析形式，并根据最大灵敏度函数来选择扰动控制器的参数。该方案不仅保留了原方案中设定值响应迅速的优点，又提高了抑制扰动性能和鲁棒稳定性。最后的仿真结果则体现出了该方案的优势。

1 两自由度控制结构

典型一阶时滞不稳定系统

(1)

本文所涉及到原结构[6]的结构图如图1所示。图中，Gc=Kc为比例控制器，Gc1为设定值追踪控制器，Gc2为扰动控制器。

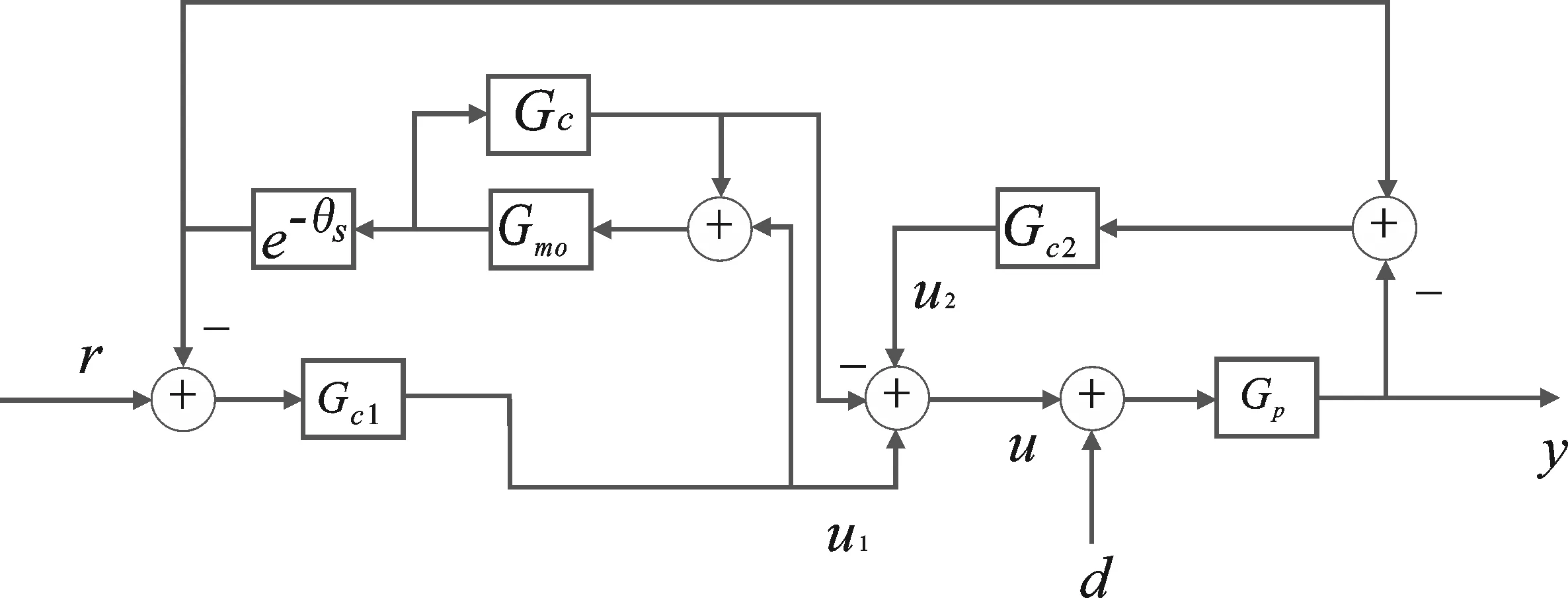
图1 两自由度控制结构图

该结构中的r、y、d、Gmo分别代表控制系统的输入、控制系统的输出、在不稳定对象输入端的扰动和为不加时滞的不稳定对象。在标称情况下(Gm=Gp)，其闭环响应为

(2)

2 控制器设计

2.1 设定值追踪控制器Gc1设计

Gc1被考虑为比例积分控制器，其形式如下

Gc1=Kpi(1+(1/Ti1s))

(3)

将式(1)和式(3)带入式(2)中，可得

(4)

将分母中的e-θs用(1-0.5θs)(1+0.5θs)替换，可得

建立多元供应体系，大力推进煤炭清洁高效利用，着力发展非煤能源，形成煤、气、油、可再生能源多轮驱动的能源供应体系。

y=

(5)

期望方程如下

CE=(λs+1)3

(6)

将期望方程式(6)与式(5)中分母对应项相等，可推导出Gc1的控制器参数

(7)

(8)

(9)

2.2 扰动控制器Gc2设计

控制系统的输出端与在对象输入端的干扰信号(在标称情况下)之间的传递函数为

(10)

扰动控制器的控制器形式为

(11)

将式(1)和式(11)带入式(10)中，可得

(12)

对分母中延迟部分使用一阶Pade近似，将等式(12)改写成等式(13)，如下

(13)

期望方程如下

CE=s4+d3s3+d2s2+d1s+d0

(14)

从式(13)可以看出，由于时滞部分的Pade近似引入了一个零点，为了防止系统产生超调，期望方程由一个4/θ的极点及3个-λd的极点构造

(15)

由式(15)和式(16)可推出扰动控制器的控制器参数

α=θ/4

(16a)

(16b)

(16c)

(16d)

(16e)

2.3 λd和λs以及设定点权重参数选择

2.3.1 可调参数λs的选值

λs越小意味着设定值追踪性能越快，但是在过程不确定性存在时，响应曲线会产生振荡。相反的，λs越大意味着在过程不确定性存在时，响应曲线会相对平稳，但是设定值追踪性能越慢。根据原方案[6]可得λs=θ为最合适的值。

λs=θ

(17)

2.3.2 可调参数λd的选值

在文献[10]中提到，在实现所要求的性能时，MS的值往往都比2大。那是因为当不稳定系统带有时滞时，不可能实现更低的灵敏度函数值。由图2和图3可知，θ/τ的值越低，挑选λd的值更加自由，反之则相反。根据相对于每个MS所对应的θ/τ值，采用曲线拟合工具生成了以下关系

(18)

图2 当θ/τ=0.2，λdτ与MS的关系图

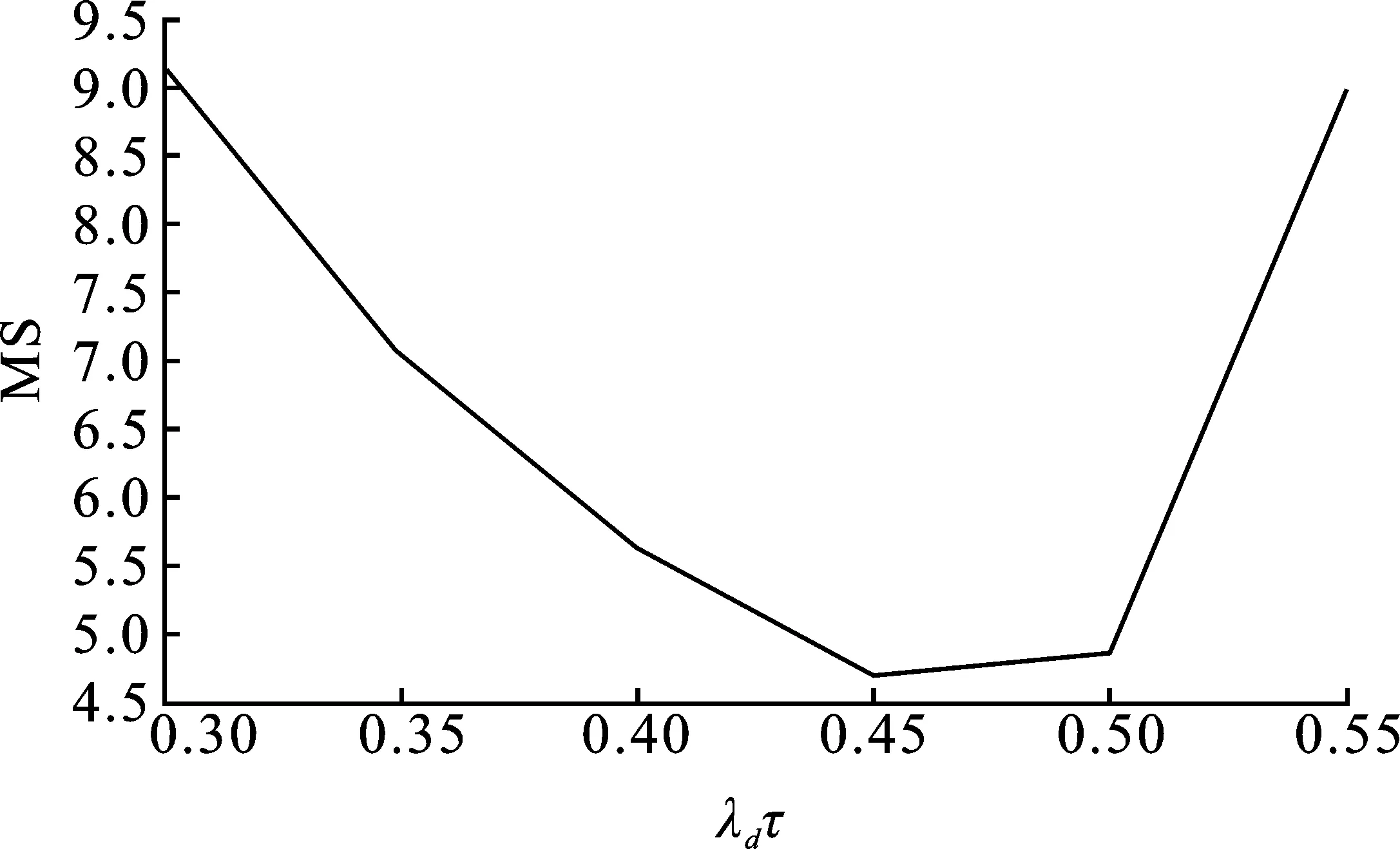
图3 当θ/τ=1，λdτ与MS的关系图

3 鲁棒稳定性分析

因为控制器参数是根据真实动力学模型的近似模型设计的，所以闭环系统不确定性的鲁棒稳定性分析显得尤为重要。根据文献[3]可知，该闭环系统鲁棒稳定性的充要条件为

‖Δm(jω)Td(jω)‖<1，∀ω(-，+)

(19)

其中，Δm为实际被控过程的乘性不确定界；Td是补灵敏度函数。

Td的表达式如下

(20)

(21)

将式(1)、式(3)和式(11)以及对时滞部分的Pade近似带入式(20)，有

(22)

当不确定性存在于过程时滞中，λd的取值应该满足的条件为

(23)

‖Td‖

(24)

同理，当不确定性存在于过程增益中，λd取值应该满足的条件为

‖Td‖

(25)

同理，当不确定性存在于时间常数，λd的取值应该满足的条件为

‖Td‖

(26)

4 仿真实验

本文通过对绝对误差积分(Integral Absolute Error，IAE)、平方误差积分(Integral Absolute Error，ISE)、全变差(Total Variation，TV)和稳定时间ts(Settling time)进行数据对比来比较系统的闭环性能。

4.1 实验1

文献[6]提出一个增益为4的比例控制器来稳定不稳定时滞对象G=e-0.5s/(s-1)，Gc1= 0.5+2/s，Gc2=1.788 7(1+(1/4.989 5s))(1+0.25s)/(0.098 4s+1)分别为设定值追踪控制器和扰动控制器。Padula and Visioli[11]的控制器Gc1=2.101 1 (1+(1/1.933 4s)) ((1+0.277 2s)/(1+0.0277 2s))和Gc2=2.093 8(1+(1/1.391 1s)) ((1+0.307 5s)(1+0.030 75s))分别负责设定值追踪和抑制扰动的作用。文献[12]提出将一个增益为1.268的比例控制器置于内环，一个比例积分微分控制器GPID=0.353 3(1+(1/1.504 6s)+0.516 6s)和时间常数为0.4设定值滤波器置于外环。本文根据式(17)和式(18)可得调参值为λs=0.5，λd=1.1。为了得到更好的控制器性能，将λd上调为1.3。因此，控制器参数为kc=4，kp1=0.5，Ti1=0.25，Kd=2.007 8，τ1=0.196 2，τd=0.201 1，α=0.125，β=0.089 7。为了增强仿真数据的说服力，本文在以下两种情况下对系统性能进行比较：在伺服情况下，当t=0时，给系统一个数值为1的设定值输入。当t=15时，在对象输入端加一个扰动值为-1的扰动信号；在摄动情况下，当t=0时，给系统一个数值为1的设定值输入。当t=35时，在对象输入端加一个扰动值为-1的扰动信号。图6为摄动情况下的系统输出，系统所给的摄动条件为假设时滞项增加20%，时间常数减小10%。由于Padula and Visioli[11]在摄动条件下不能稳定不稳定系统，因此，Padula and Visioli 这条线并不在图5中。

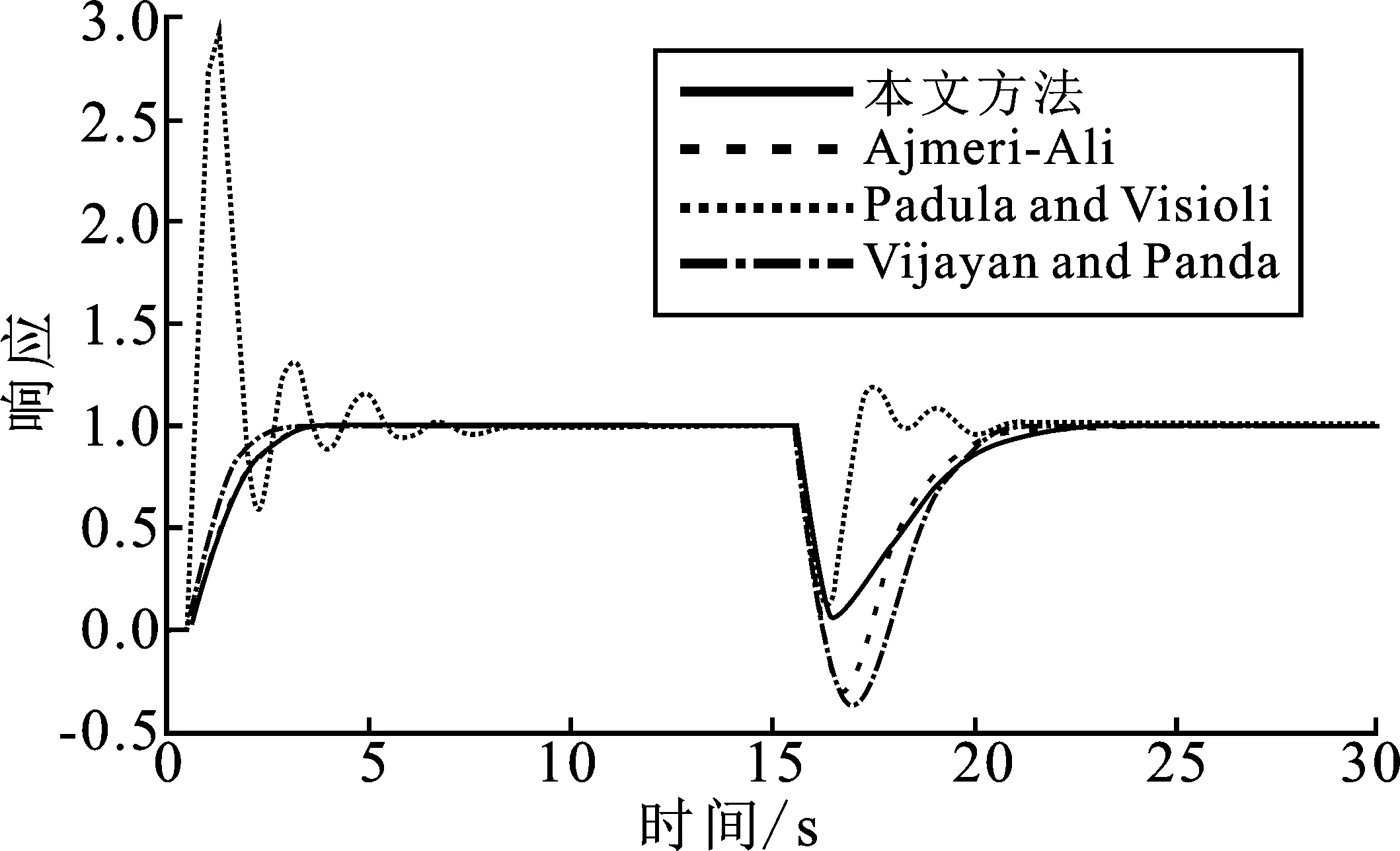
图4 标称情况下的阶跃响应

图5 摄动情况下的阶跃响应

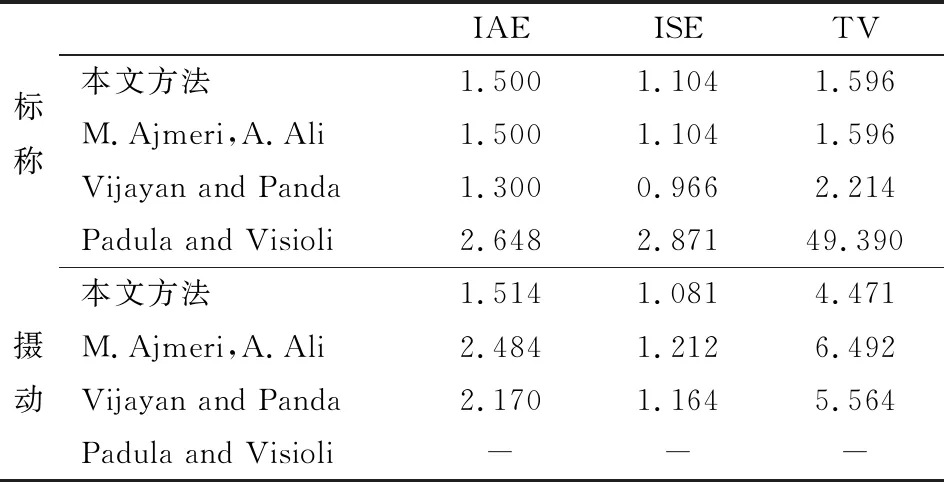
表1 设定值追踪性能比较

由图4、表1和表2中标称情况下的性能指标对比可知，在标称情况下，Vijayan and Panda[12]与其他方案对比，其设定值的追踪性能更加优越；Padula and Visioli[11]与其他方案对比，其抑制扰动性能更加优越。又由图5、表1和表2中摄动情况下的性能指标对比可知，摄动情况下所提方案IAE、ISE、TV都比其它方案小，表明所提方案的鲁棒稳定性比其他方案优越。又因为Padula and Visioli[11]在摄动情况下不能稳定不稳定系统，并且文献[6]中指出在许多控制应用中抑制扰动性能比设定值追踪性能更加重要。因此，可以认为本文所提改进方案最佳。

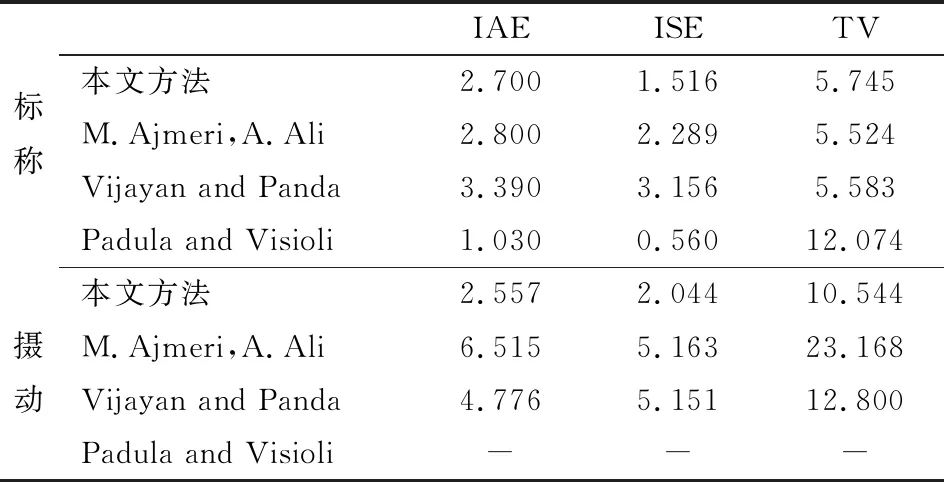
表2 抑制负载干扰性能比较

4.2 实验2

一个具有多个稳态解的等温化学反应器的数学模型为[8]

(26)

其中，Q为进口流量；Cf为进口浓度。操作参数值如下：Q=0.033 33 L·s-1，V=1 L，k1=10 L·s-1，k2=10 L·mol-1[8]。线性操作变量C=1.316的传递函数为3.433/(103.1s-1)。文献[6]中的控制器参数设置为kc=2.543 7，kp1=0.375 4，Ti1=10，kp2=1.066 5，Ti2=121.066 3，α=10，β=5.155 6。所提控制结构的调参选值为λs=20，λd=0.037。其控制器参数设置为kc=2.543 7，kp1=0.375 4，Ti1=10，kd=1.331 7，τi=0.008 6，τd=7.730 8，α=5，β=3.754 4。在t=0时，设置设定值大小为1.316～5，在t=1 000时给不稳定对象输入端加扰动值大小为0.4，摄动条件为假设时滞项增加20%。标称系统响应图和摄动系统响应图分别为图6和图7。从图6可知，本方案抑制扰动性能效果比文献[6]中的模型好。由图7可知，本方案稳定时间短、振幅小。因此，所提控制结构鲁棒稳定性和抗扰动性能更加优越。

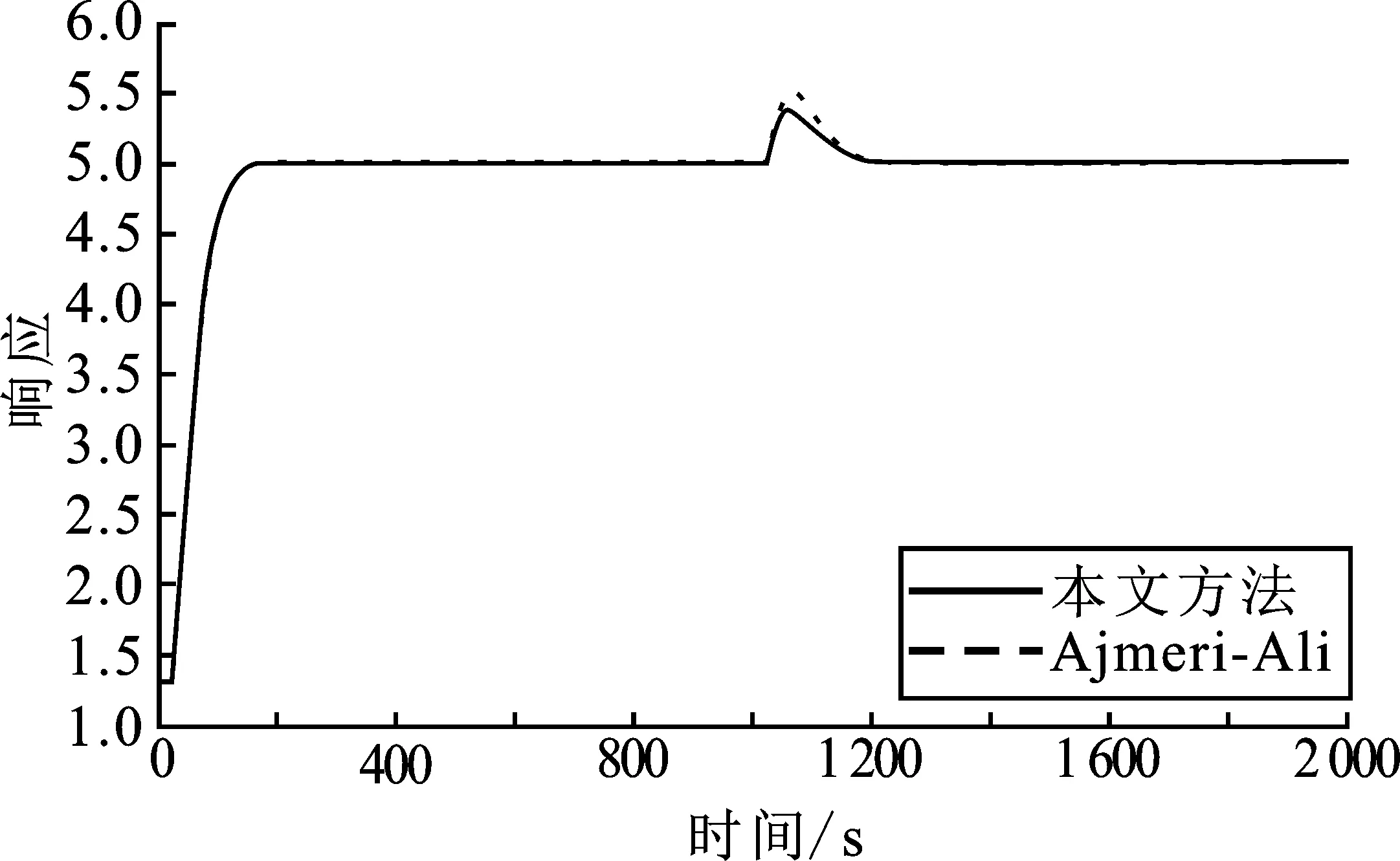
图6 标称情况下的阶跃响应

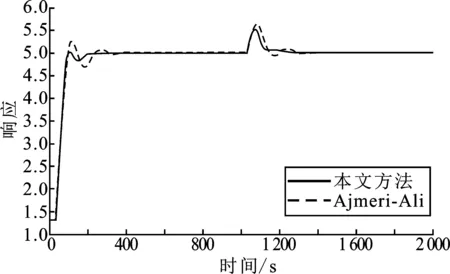
图7 摄动条件下的阶跃响应

5 结束语

本文采用文献[6]中所提出的结构，将扰动控制器改为带超前滞后项的PID形式。从仿真结果可以看出，该策略能够提高原结构的抑制扰动性能和鲁棒稳定性，解决了在工业和化学实践中带时滞一阶不稳定系统难以控制的问题。当然，本文也有不足和需要改进的地方，例如只考虑了带时滞的一阶不稳定系统。从目前来看，虽然经典PID的研究已渐成熟，但是系统性能和鲁棒稳定性仍然有提高的空间。