基于离散元与有限元耦合的有砟道床沉降特性研究

王 桐，王立华，陈佳明，栗先增

(昆明理工大学 机电工程学院，云南 昆明 650500)

铁路作为我国的重要基础设施，在交通运输体系中占据重要地位，也是目前应用最广泛的运载方式之一，对我国的经济建设和发展有着十分重大的意义。由于我国铁路近几年发展迅速，且与各个领域之间的交叉融合越来越多，所以对于铁路方面的研究也愈加深入。有砟铁路作为我国铁路运载的重要组成部分，是铁路发展的基础，对其深入的研究就显得尤为重要。有砟轨道道床质量对于保障列车运行稳定安全方面具有重要意义。

在对有砟铁路进行研究时，由于组成道床的道砟属于离散体颗粒，而道床上部轨枕属于连续体，所以在对二者进行分析时不能使用单一的方法。有限元法只能从宏观上反应轨枕与道床的整体特性。Ishikawa[1]等通过室内试验研究有砟道床在定点载荷和移动载荷作用下的力学行为。其结果表明，在移动载荷作用下有砟道床产生的塑性变形比定点位移作用下的大。Mc Dowell[2-4]等基于真实颗粒外形的最小半径离散单元数值模型的构造方法，用所生成的组合球单元对复杂外形的道砟颗粒进行了模拟，并对比分析了组合单元颗粒与球形单元颗粒在荷载作用下的力学特性。井国庆[5]等基于二维离散单元法颗粒软件Particle Flow Code 2D(PFC 2D)，建立了道砟轨枕离散单元模型，研究了列车循环荷载作用下道砟颗粒破碎与轨枕沉降的关系。Shaer[6]等采用等比例缩减尺寸的铁轨-枕木-道床-路基模型得到整体道床的沉降与枕木和道砟的振动加速度密切相关。高亮等[7-8]利用离散单元法，分别建立球形道砟颗粒和颗粒簇形成道砟颗粒的轨枕与散体道床的离散元模型，对比分析了两种不同模型在循环荷载下的力学性能，并利用离散元颗粒数值模型构造道砟颗粒模型。同时，在此基础上建立了循环荷载道砟箱数值模型，研究在列车高速及重载线路条件下，道砟级配对散体道床沉降力学特性的影响情况，并从细观角度分析了散体道床的沉降原理。但若要同时从宏观和微观方面对有砟道床进行分析，就需要引入有限元和离散元耦合的方法。

针对离散元与有限元耦合方法的研究，冯春[9]将对有限元模型进行加载达到临界状态时，把有限元替换为离散元研究。严颖等[10-12]在离散元与有限元的接触面处提出一种新的接触算法，实现有砟铁路轨道的离散元-有限元耦合法的研究分析，又通过镶嵌单元模拟来达到耦合的方式并通过Fortran语言编程计算有限元与离散元的耦合结果。严颖等依据接触面上的能量守恒原理，确定两种介质间的接触力实现离散元-有限元单元区间力子参数传递。尹超[13]利用MATLAB编制程序接口，通过间接计算实现离散元软件与有限元软件的数据计算与传递。

上述文献都是基于耦合方法研究轨枕与散体道砟颗粒的相互作用力，需要通过外部程序来进行有限元和离散元颗粒之间的数据传递。为简化数据之间传递的繁琐过程，本文采用有限元软件得到轨枕网格坐标，导入离散元中用离散元颗粒以及键连接构造轨枕模型。后采用球颗粒组合模型构造非规则道砟，得到缩小比例工程尺度的枕木-道床离散元模型。本研究通过对轨枕施加循环正弦激振，研究了轨枕和散体道砟颗粒的相互作用和轨枕的受力、变形情况。此外，本文还研究了不同激振频率对有砟道床力学性质的影响，得到道床的沉降规律并探究了道床累积沉降的内在机理。

1 有砟道床的离散元模型

1.1 典型形状道砟模型构建

离散单元法(Discrete Element Method，DEM)主要用于离散颗粒物料研究领域。非规则形状颗粒建模耗费大量时间，且模型精度对颗粒间的动力学响应特性有较大影响，故本文采用离散单元法构建道床模型，旨在提高非规则形状颗粒建模效率及精度。在有限元软件中建立轨枕模型并划分网格，同时获取网格单元坐标信息，并在离散元软件中设置接触半径及物理半径，然后通过工程离散单元法(Engineering Discrete Element Method，EDEM)中的应用程序编程接口实现多球快速聚合颗粒建模。道砟颗粒的形态会对散体道床的动力特性产生显著的影响，构成簇颗粒的球单元越多，其对道砟形态的描述就越真实。利用以上构造方法可以对任意形态的道砟进行构造。考虑到离散元计算效率，本文采用4～10颗小球颗粒组成的簇颗粒单元对不规则道砟颗粒进行近似构造，模型示意图如图1所示。组成簇颗粒的球颗粒之间存在很大的重叠量，且保证了道砟内部不存在孔隙。颗粒簇在离散元模拟计算中不考虑其破碎，每个颗粒簇在运动过程中被视为一个整体，颗粒簇之间采用线性接触模型去模拟颗粒之间的接触行为。

图1 不同形状的铁路道砟颗粒簇模型

正常工作的有砟铁路使用的道砟颗粒尺寸一般在37～54 mm之间，如上图所示粒径范围分别在表1道砟级配中的30～45 mm、45～60 mm、>60 mm这3个范围内选取。

表1 道砟级配

道砟与道砟之间，道砟与构成轨枕的离散元颗粒间的接触参数如表2所示

表2 道砟间的接触参数

1.2 节点坐标提取与离散元软件颗粒的替换

在离散元中将分析对象视为充分数量的离散介质进行计算，其将每个离散颗粒作为一个单元，然后求解出每一时刻中颗粒的相互作用、接触力及离散单元的运动状态。随后，通过引入时间步长的方式，依次求解出离散单元体的运动形态。离散单元体一般使用球形颗粒，根据实际问题的不同，将颗粒模型分为软球模型和硬球模型两种，本文所采用的是软球模型。

利用离散元软件EDEM所提供的应用程序编译外接口(Application Programing Interface，API)编写插件来自定义接触模型、颗粒生成、外部耦合及颗粒模型[14]。轨枕颗粒建模仿真实验中利用Visual Studio编程软件创建的颗粒工厂动态链接库文件，得到颗粒ID、颗粒三维坐标、颗粒实际物理半径，颗粒接触半径等所需的模板颗粒信息，并对颗粒进行替换。考虑到颗粒替换得到的模型与颗粒之间的粘结键及仿真所需要的计算时间，文中将组成轨枕的颗粒小球实际物理半径设置为1.25 cm，颗粒接触半径设置为1.6 cm。由离散元颗粒替换构成的轨枕模型如图2所示。

图2 离散元颗粒替换构成的轨枕

1.3 轨枕-散体道床耦合模型的建立

将道砟颗粒模型建模后，根据已有相关研究[15]和道砟颗粒模型的尺寸建立道砟箱模型。当道砟容器的尺寸大于颗粒平均粒径的8倍时，容器的边界效应可以被忽略。本文建立的道砟颗粒模型的平均粒径不超过45 mm，容器最小要求尺寸为340 mm，建立铁路道砟箱三维模型，其中道砟箱的尺寸为1 000 mm×700 mm×600 mm(长×宽×高)。考虑到仿真所面临的时间和内存问题，本文仅建立由一根轨枕和有砟道床组成的离散元模型。简化模型中有砟道床及轨枕的尺寸与实际道床及轨枕的尺寸比例为1∶8，轨枕由简单的长方体简化代替。

在有限元软件中对节点数据进行处理后，在离散元软件中，设置单独母体小球，在到达需要放置的轨枕位置后，通过颗粒替换将离散元颗粒按照轨枕网格划分坐标在离散元软件中排布组合成新轨枕。建立符合要求的有砟道床离散元模型，如图3所示。

图3 轨枕与道床的三维离散元模型

完成轨枕与道床的离散元模型建立后，为其添加接触参数，确定轨枕颗粒和道砟颗粒运动边界条件。由于对道砟颗粒的研究需要确定颗粒间准确的接触力变化情况，且暂不考虑颗粒破碎的情况，因此采用Hertz-Mindlin(no slip)无滑动接触模型。由于轨枕由散体颗粒构成，需要设置bond键来连接各个离散元颗粒以达到整体作为轨枕的效果。轨枕采用Hertz-Mindlin with bonding基础模型。用于模拟破碎、断裂等问题时，则采用小颗粒粘结成大块物料。外力作用下颗粒间粘结力会发生破坏，从而产生破碎及断裂效果，但本文不考虑轨枕的劣化和破损问题，故bond键强度设置较大。最终所确定的道砟颗粒与颗粒，颗粒与轨枕间的恢复系数、静摩擦系数和动摩擦系数如表3所示。

表3 轨枕粘结模型物理参数

由于无法直接对轨枕施加激振载荷，因此需要将作用在轨枕上的载荷转化为不同的形式施加在轨枕上。将轨枕所受到的激振力转化成位移的形式输入到轨枕上，即在仿真过程中通过在轨枕两侧施加激振源，对激振源设置位移函数，水平激振力属于正弦激振力，存在频率和幅值。因此将水平激振力转化成频率和位移幅值的形式施加在轨枕上，并通过改变激振频率来对不同激振频率下轨枕的沉降状态进行研究。对轨枕施加激振，完成稳定过程仿真，以离散元软件为主体来实现耦合过程。

2 稳定作用下轨枕受力及道床动力特性分析

2.1 轨枕下方不同区域的速度变化趋势

在轨枕下方的道砟在稳定作用下，道砟的移动方向整体向下，其中以轨枕下方的道砟颗粒尤为明显。为了直观分析不同载荷频率对道床的冲击程度，如图4所示，给出了载荷频率为36 Hz时枕木受到稳定作用，道床中间厚度1 cm垂向截面区域内所有道砟颗粒的速度分布图。可看出枕木两侧道砟颗粒的速度均较小，说明稳定载荷对轨枕下方道砟起主要作用。道砟颗粒的速度幅值呈现近似扇形的衰减，且轨枕下方道砟颗粒具有更加明显的垂直向下运动趋势，越靠近轨枕中心的道砟颗粒，其垂向速度响应越大。

轨枕在受到激振时，向左右两侧产生微小位移，在轨枕向左向右移动时，砟肩部分的道砟随着轨枕产生同向位移。由于轨枕下方道砟颗粒始终为向下移动，所以在激振影响中，道砟不断向下移动，达到重新排布效果。整个过程中，轨枕下方道砟不断下沉，使上方轨枕下沉。

2.2 轨枕的力学特性分析

选取轨枕底部颗粒，提取该颗粒在稳定过程中的位移量来得到轨枕整体的沉降量，如图5所示，颗粒在稳定过程中的沉降量为20 mm左右。由图中可以看出，在对不同激振频率下道床稳定作业过程的仿真中，随着稳定作业的进行道床轨枕沉降量逐渐增大，并且随着激振频率的增加轨枕总沉降量逐渐增大，在36 Hz时达到最大值；当激振频率继续增大时，沉降量又逐渐减小。

图5 轨枕沉降量与时间的关系

3 设计道砟箱试验与模型验证

3.1 道砟箱试验的设计

根据前文轨枕和道砟颗粒的选型设计搭建试验平台，如图6所示，建立与仿真同比例的道砟箱试验。文中所使用的箱体尺寸(长×宽×高)为1 000 mm×700 mm×550 mm，所用材料为3 mm厚钢板。通过安装偏心振动电机在水泥轨枕上部来模拟稳定过程，并使用调频器达到不同激振频率的效果。该振动电机可以提供水平方向的激振力，在垂直下压力方面只考虑轨枕和振动电机的质量。

图6 道砟箱试验

为研究试验中模拟稳定作业轨枕沉降量的变化规律，通过激光测距仪可以准确地得出动力稳定作业过程中道床的垂向位移和轨枕的水平激振幅值以及水平激振频率与轨枕沉降的关系。将激光测距仪安装在轨枕正上方距离3 cm处，同时避免与道砟箱接触，防止振动对测量产生影响。在进行测量时，测距仪的激光照射到轨枕的振动电机安装钢板上，当模拟稳定作业过程开始时，激光测距仪发出红外线照射到轨枕上方的平滑钢板上进行数据采集，得到每一个时刻轨枕与激光发射口的距离大小。将初始位置设置为零点，即可得到轨枕的沉降量。

图7 激光测距仪实物图

动力稳定车在对劣化道床进行稳定作业的过程中，水平激振频率的工作频率范围是0～45 Hz，刘畅[16]得到的动力稳定作业过程中最优激振频率为30 Hz；项永志[17]通过仿真得到动力稳定作业最优激振频率为31～33 Hz。本文建立的试验平台为小型道砟箱试验平台，由于激振电机的频率限制，激振频率在30 Hz以下的激振作用振动比较微弱，所对应的稳定效果不明显，因此最终选择设置梯度递增的激振频率，分别为30 Hz、32 Hz、34 Hz、36 Hz、38 Hz和40 Hz，共6组。由于偏心振动电机的额定频率为50 Hz，无法直接改变其频率，因此通过变频器来调节电机的频率，达到本文对于不同频率的试验要求。

3.2 数据的提取与验证

在比例缩小模型实验中，使用激光测距仪测量轨枕下沉量，与上文中的轨枕下沉量进行对比分析。为方便统计数据和计算，在仿真模拟中选取如图8所示轨枕底面小球颗粒编号11 316作为分析对象，提取此处颗粒在稳定过程中的位移来进行数据对比分析。

图8 道砟颗粒选取位置

提取此位置道砟颗粒在稳定过程中的位移即轨枕的沉降量，如图9所示得到仿真过程中轨枕颗粒的位移情况，可以发现在稳定过程中，轨枕的沉降量随着激振频率的增加而增大，当激振频率为36 Hz时达到最大值，之后随着频率的增加逐渐减小。

由图9可知激振频率不变时，动力稳定作业下道床沉降趋势与循环载荷作用产生的道床沉降趋势基本相同。由于道砟颗粒相互接触时具有一定的弹性，因此道床沉降过程具有一定的反复，试验结果和文献[16]中动力稳定下的道床沉降趋势基本相同。这是因为道床初期比较松散，密实度低，稳定作业下道砟颗粒之间迅速密实，沉降急剧增大，随着稳定作业的进行，道床逐渐密实，稳定性逐渐提高，道床沉降量逐渐变缓；当激振频率增加时，道床沉降量呈现先增大后减小的趋势，在36 Hz时达到最大，其道床的沉降稳定效果最好。

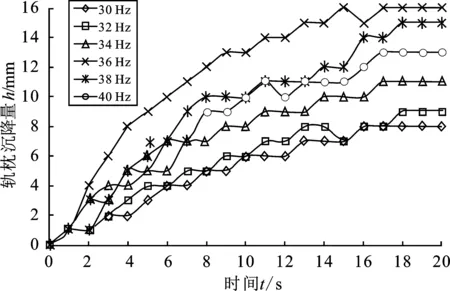
图9 道床沉降趋势图

将实验得到的轨枕随时间变化的沉降量变化情况绘制成轨枕沉降量相对于时间变化关系图像，并绘制经过仿真得出的轨枕沉降与时间关系图像对比实验及仿真结果。如图10所示，将离散元有限元耦合建模与试验获取的数据结果进行对比可知，试验获得的轨枕沉降曲线由于在道砟箱堆放道砟时道砟颗粒之间空隙较大堆叠稀松，所以在激振在初期沉降量上升较快。试验与仿真的沉降趋势基本一致，说明本文建立的有砟道床仿真分析模型是可靠的，所选取的参数正确，所确定的边界条件合理，仿真分析结果有效。

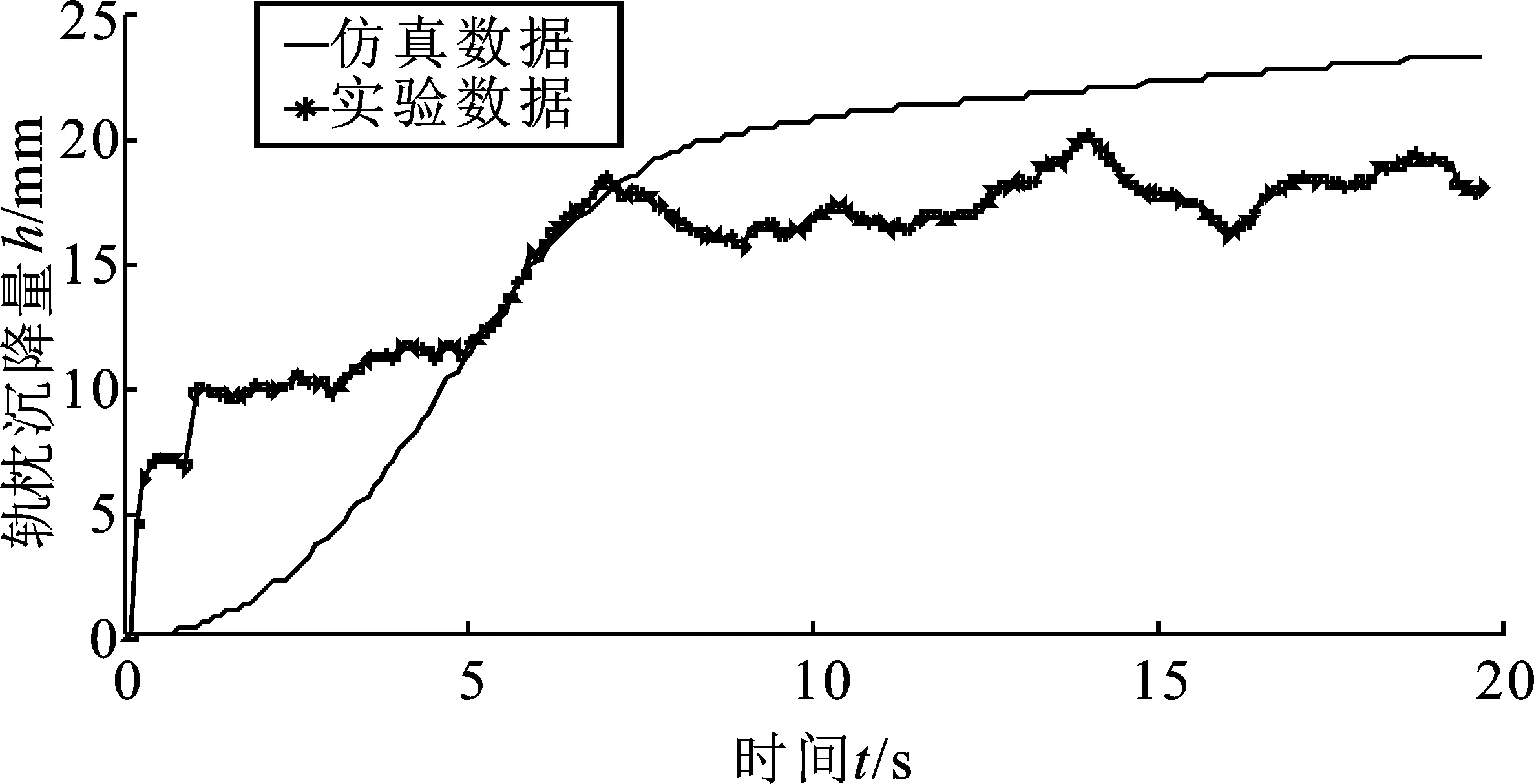
图10 实验与仿真对比图

经过对轨枕在36 Hz激振力作用下仿真得到的轨枕沉降量与时间变化可看出其趋势变化规律形如指数函数。为了方便研究轨枕沉降量变化规律并得到普遍性结论，文中对仿真得到的轨枕沉降量变化趋势进行指数函数拟合，指数函数阶数为2，拟合结果如图11所示，则36 Hz激振力影响下轨枕沉降量与时间的演化规律大致服从图中拟合过后得到的曲线发展规律。

分析处理得到道床累计下沉量随时间变化的函数模型方程为

f(x)=-106×e-0.006 388x+106×e-0.000 638 7x

(1)

式中选取的常数项为最佳数值，即拟合度最高的沉降量计算式。当常数项在符合要求的区间时，可对相应的激振频率进行拟合，可靠率达95%。

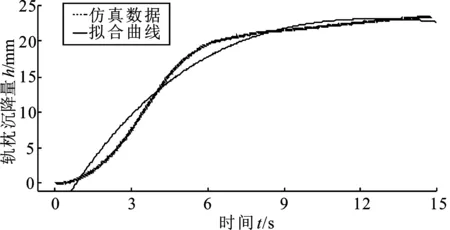
图11 拟合曲线与仿真曲线对比图

4 结束语

文中通过有限元软件建立了缩小尺寸轨枕模型，得到网格划分后的节点坐标，在离散元软件中通过颗粒替换将轨枕单元颗粒按照节点坐标排列，得到有砟轨道结构的三维离散元模型。建立相应道砟箱模型，分析在稳定载荷下轨枕对道砟颗粒的作用情况、轨枕的受力情况和应力分布情况。

本研究根据仿真模型搭建了试验平台，综合分析离散单元法在仿真道床实际状态的优势和特点，通过将模拟仿真分析结果与实际试验数据对比，验证了此耦合方法在稳定作业过程中仿真道床实际状态的可行性和有效性，并利用离散单元法进一步深入研究。本研究发现轨枕在钢轨与道床之间，上部稳定车传递过来的激振效果通过轨枕来影响道床，且与下部结构散体道砟颗粒直接接触。轨枕正下方道砟颗粒振动速度均随着道床深度的增加呈扇形迅速衰减，且随着稳定作业的进行，轨枕下方道砟颗粒不断向下移动，当激振频率为36 Hz时，道床沉降量最大。利用EDEM软件进行了作业过程的模拟仿真并提取了相关数据，得到了不同作业工况下任意时刻道床下沉量等相关数值，并给出了沉量随时间变化的函数模型方程。