盘形锻件等效应力分析及神经网络预测

初红艳，赵凯林，程 强

(1.先进制造技术北京市重点实验室，北京 100124； 2.北京工业大学先进制造与智能技术研究所，北京 100124)

钛合金是航空零部件的主要材料，具有强度高、耐热性好、耐蚀性好、抗氧化能力强等特点[1]. 航空盘形锻件，如端盖、密封件和紧固件等均由钛合金制造[2]. 端盖作为发动机上典型的盘形锻件，在使用过程中残余的等效应力会降低疲劳性能，并且对航空发动机的使用性能、可靠性和寿命等产生负面影响. 等效应力分布及特性从根本上影响着微观组织状态、力学性能、缺陷等. Xu等[3]采用实验的方法，研究了盘型锻件表面及心部的应力分布规律，并分析了应力与位错、动态再结晶的关系；惠媛媛[4]采用实验及数值模拟的方法，研究了圆环镦粗过程的内部应力场分布规律；Lin等[5]采用离散位错模拟方法，研究了在均匀温度下残余应力和热位错对金属基材料的力学性能影响；张盛明等[6]采用交互积分法，分析了热应力对双材料表里面裂纹的应力强度因子的影响；Stern等[7]提出用于分离二维复合型应力强度因子的方法，从能量角度出发，不用考虑裂纹前沿复杂的应力情况，被广泛用于分离二维双材料界面裂纹应力强度因子研究中；孙宇幸等[8]研究了不同应力集中系数和应力比与疲劳强度之间的关系，分析了疲劳裂纹和韧窝的微观形貌.

上述研究大多从单一节点或单一因素来分析应力对锻件质量的影响，较少从整体上分析应力对锻件质量的影响；同时，实际生产中实现在线应力综合评价预测及工艺评价的研究较少. 本文利用DEFORM-3D软件对钛合金盘形锻件进行锻造过程模拟并进行了实验验证，分析了盘形锻件等效应力分布规律. 基于仿真模型设计正交实验，建立盘形锻件应力综合指标模型，并应用反向传播(back propagation,BP)神经网络实现生产中在线预测盘形锻件应力综合评价值，以期达到通过工艺参数可直接实现分析盘形锻件应力状况的效果，并间接通过应力综合评价值实现锻件工艺过程评价分析. 实现锻件综合质量的智能预测、质量控制，为后续锻造工艺改进提供依据.

1 盘形锻件有限元模型建立与仿真实验分析

1.1 有限元模型建立

采用DEFORM-3D软件建立盘形锻件的有限元仿真模型，结合弹塑性有限元分析方法进行热力学耦合仿真，考虑坯料和环境、坯料和模具、模具和环境之间的热传导过程，同时考虑坯料和模具之间，在锻造过程中摩擦及锻造速度变化产生的温升效应[9]. 坯料材料为Ti-13C11Cr3Al，模具材料为4Cr5MoSiV1；坯料尺寸为φ60 mm×45 mm，锻件最大直径为122 mm，最小直径为65 mm，锻件高度为35 mm，最大圆角为12 mm，最小圆角为8 mm，侧表面均匀分布6处支撑；在锻造过程中定义模具为刚体，坯料为弹塑性体；应用整体划分法对坯料进行网格划分，设置最小网格单元为0.8 mm，尺寸比率为3. 图1、2为坯料温度930 ℃、模具温度300 ℃、下压速度60 mm/s、室温25 ℃、模具摩擦因数0.3的航空盘形模锻件的仿真结果.

由弹性矢量叠加原理分析得，温度应力、组织应力、残余应力以等效应力[10]的形式表现出来. 图1为加载完成后等效应力分布图，图2为卸载后等效应力分布图. 由图1看出加载完成后锻件侧表面等效应力为734.38～881.26 MPa，上表面等效应力为587.57～734.38 MPa，心部等效应力为146.88～293.75 MPa. 锻造生产过程中产生的等效应力会对锻件性能及质量造成较大影响，须及时预警并改进工艺.

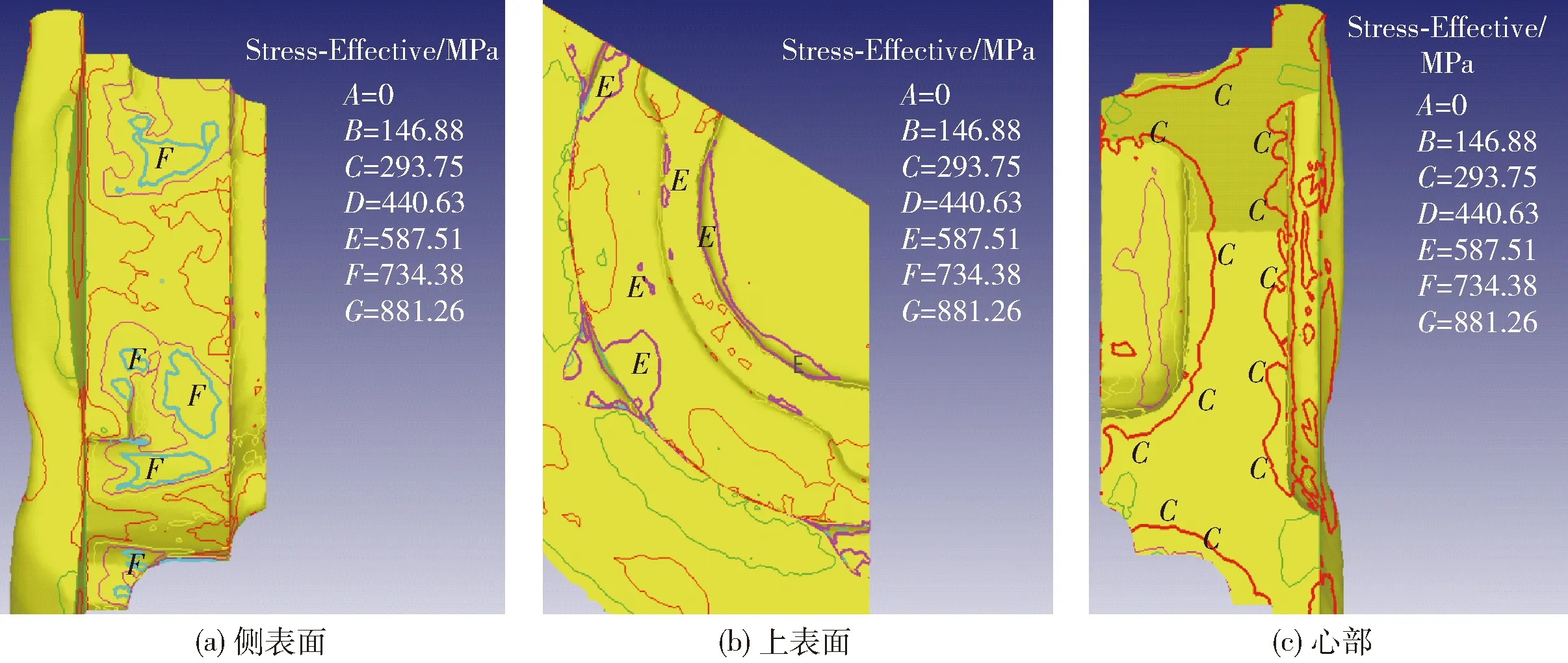
图1 加载完成等效应力分布图Fig.1 Load complete equivalent stress distribution diagram

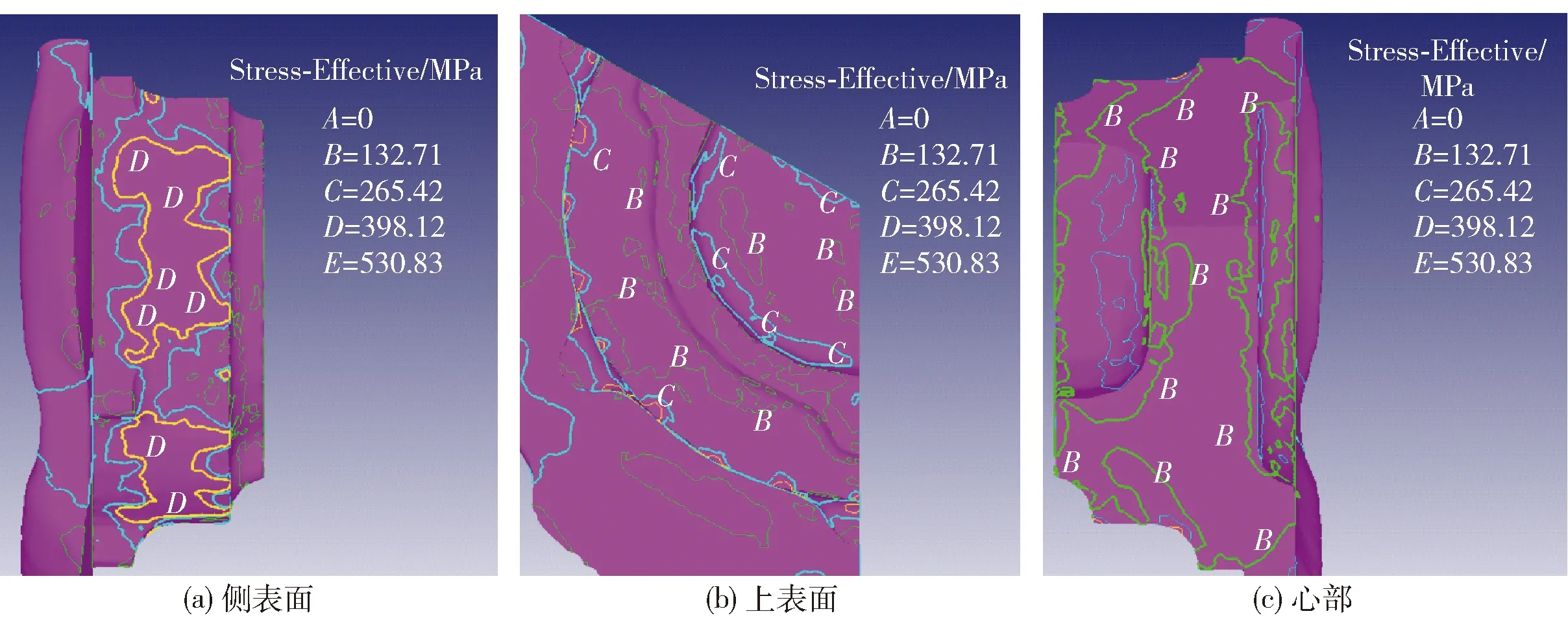
图2 卸载后等效应力分布图Fig.2 Equivalent stress distribution after unloading

1.2 实验验证

为验证仿真的正确性，本文进行了应力测试实验. 锻造过程在某航空企业进行，实验材料选用Ti-13C11Cr3Al钛合金. 本文测试方法采用X射线衍射法，根据钛合金材料选择Co靶材，选择比靶材原子序数小1或2的滤波片.

根据GB/T 7704—2008《无损检测X射线应力测定方法》，本次实验采用测点法[11]对锻件几个关键位置进行应力测试. 图3(a)为锻件实物图，图3(b)(c)所示为锻件测点示意图，将锻件分成3个部分A、B、C，每个部分测点位置相同.

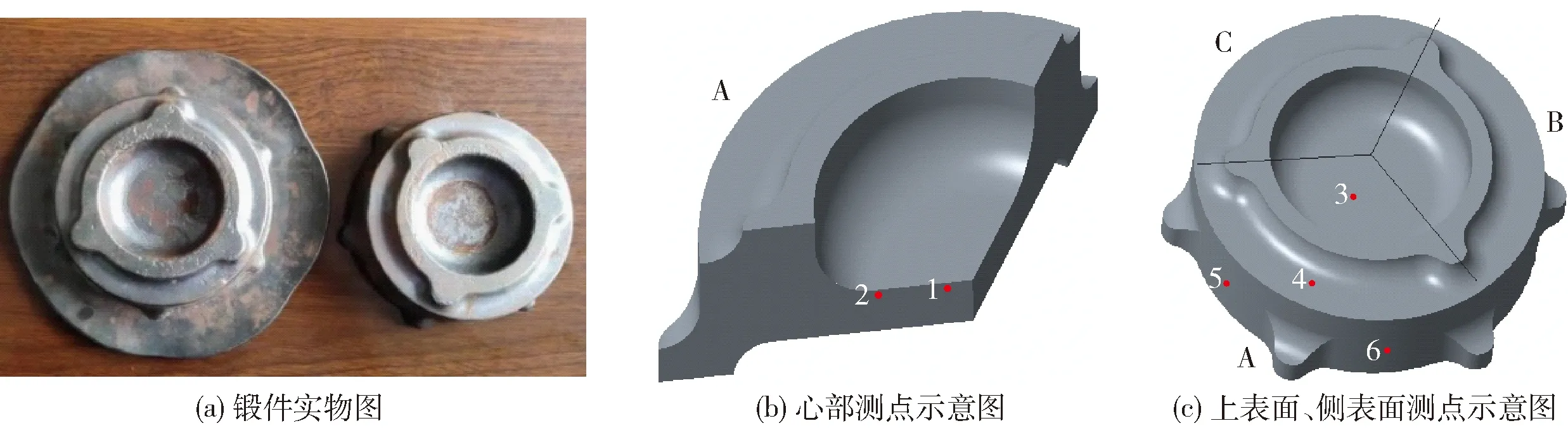
图3 锻件、测点示意图Fig.3 Schematic diagram of forging and measuring point

测试取点如图3所示，表1为应用X射线衍射法测试锻件卸载后等效应力结果；表2为实验与仿真测得卸载后等效应力平均值的对比结果，经过实验结果与Deform仿真对比发现误差相差不大，应力平均值最大相对误差未超过10%，说明了Deform仿真的结果与实验结果较为一致，验证了仿真的正确性.

表1 盘形锻件应力实验结果

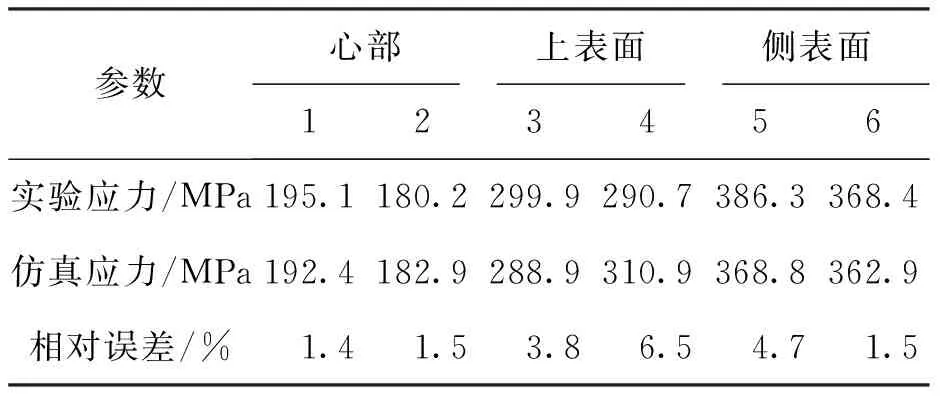
表2 盘形锻件实验与仿真结果对比

1.3 正交实验设计与分析

锻造生产过程中等效应力会对锻件力学性能等质量造成较大影响. 分析得锻造加载完成后等效应力较大，通过分析加载完成后等效应力为后续在线等效应力综合评价模型建立做准备，既可实现等效应力综合评价预测，又可根据预测值间接实现在线工艺评价.

因仿真数据较为准确，为了节省时间及生产成本，通过仿真数据进行正交实验设计，获取建立综合应力指标及建立BP神经网络的数据. 分别以锻件侧表面等效应力M1、上表面等效应力M2、心部等效应力M3为目标，以坯料温度T1、模具温度T2、下压速度V、室温T3、摩擦因数μ为实验因素，每个因子选取4个水平进行实验，即选取L16(45)的正交表. 由钛合金相变温度及钛合金锻造工艺[12-13]分析,确定T1在930 ℃附近取值、T2在300 ℃附近取值、V在60 mm/s附近取值、T3在30 ℃附近取值、μ在0.4附近取值，在仿真过程中假设了热传导系数、空气对流系数、热交换系数固定，方案及实验结果如表3、4所示.

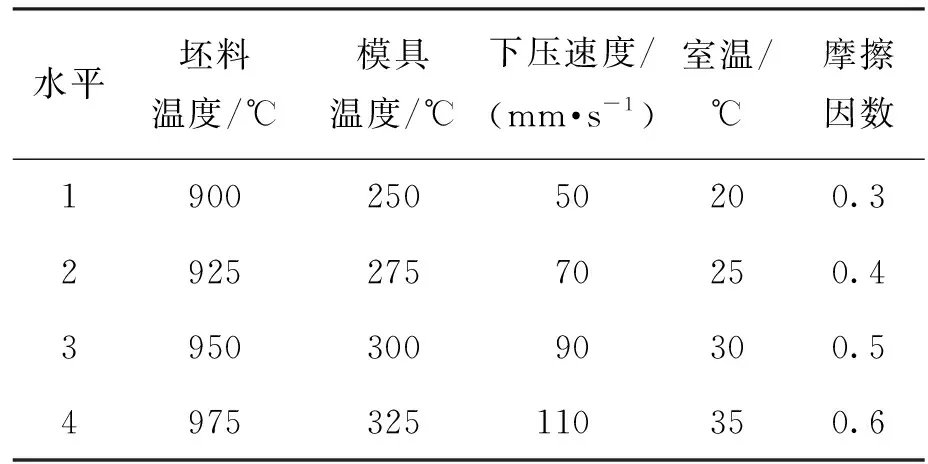
表3 因素水平正交实验设计

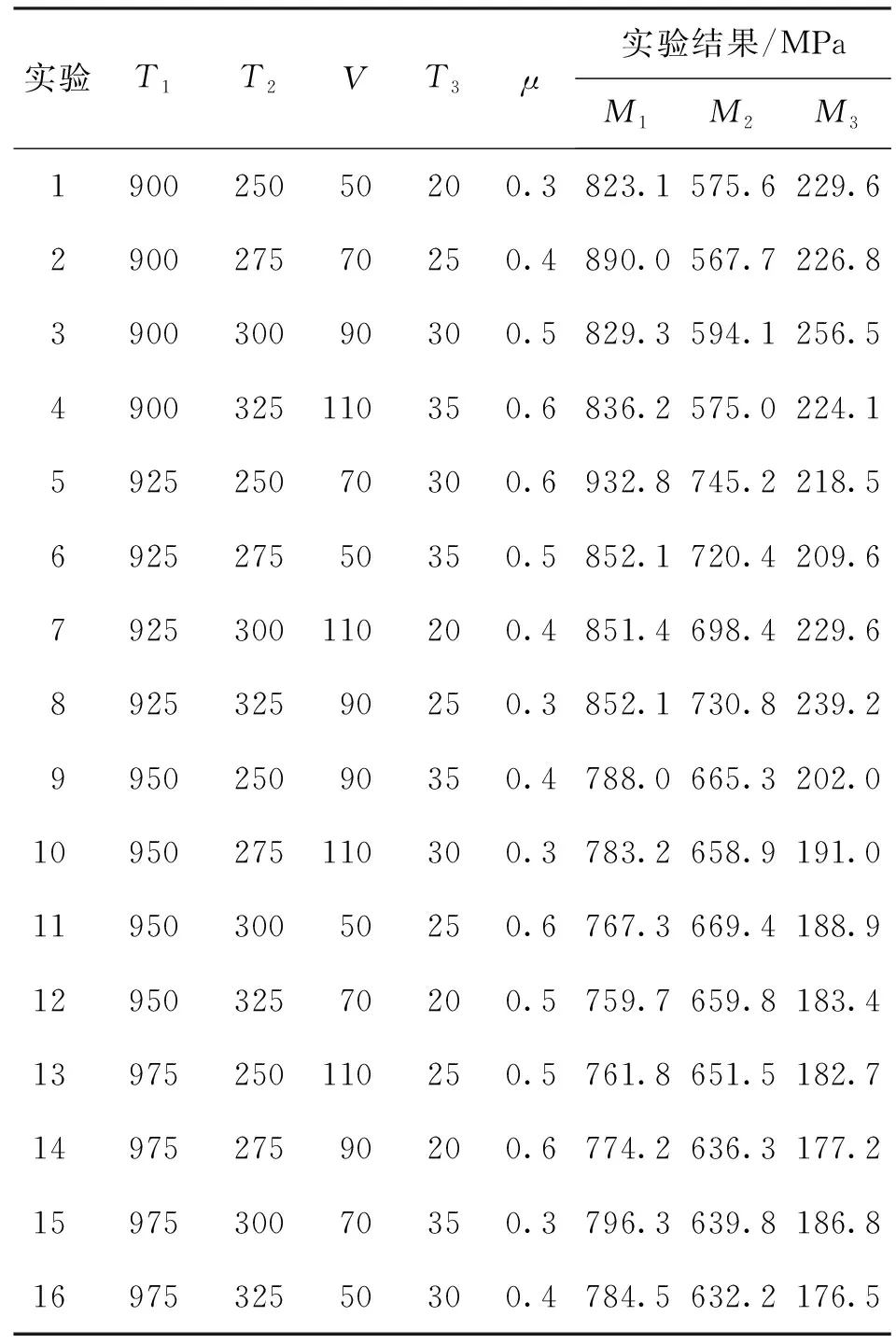
表4 实验方案及部分实验结果

1.3.1 基于灰关联分析法的因素影响程度分析

为了定量分析仿真过程中影响因素对应力的关联程度，采用灰关联法对实验结果进行分析，建立如下计算步骤.

1) 归一化，以影响因素X为比较序列，应力M为母序列，分别对序列进行归一化：

(1)

(2)

式中：X*为归一化后比较序列，M*为归一化后的母序列.

2) 求应力关联系数，i=1,2,…,n；j=1,2,…,p. 其中n为样本个数，p为特征个数，由文献[14]可知计算公式如下：

(3)

应用上述公式分别求影响因素对不同位置应力的关联系数，式中：Δji(k)=|mj(k)*-xi(k)*|,为mj(k)*和xi(k)*的偏差序列，xi(k)*为第i类影响因素对应的第k个数据，mj(k)*为第j类应力对应的第k个数据；ξij(k)为关联系数，且0<ξij(k)<1；ρ∈[0,1],ρ为分辨率，通常ρ取0.5.

3) 求关联程度Γij，分别求每个因素对各位置应力的关联程度，其中：j=1,2,…,p.

(4)

4) 求综合关联程度ξi，即每个因素与应力的关联程度：

ξi=φ1Γi1+φ2Γi2+φ3Γi3…φpΓip

(5)

式中：i=1,2,…,n;φ1,φ2,…φp由综合指标模型贡献率确定，贡献率公式见第2章.

1.3.2 结果分析

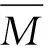
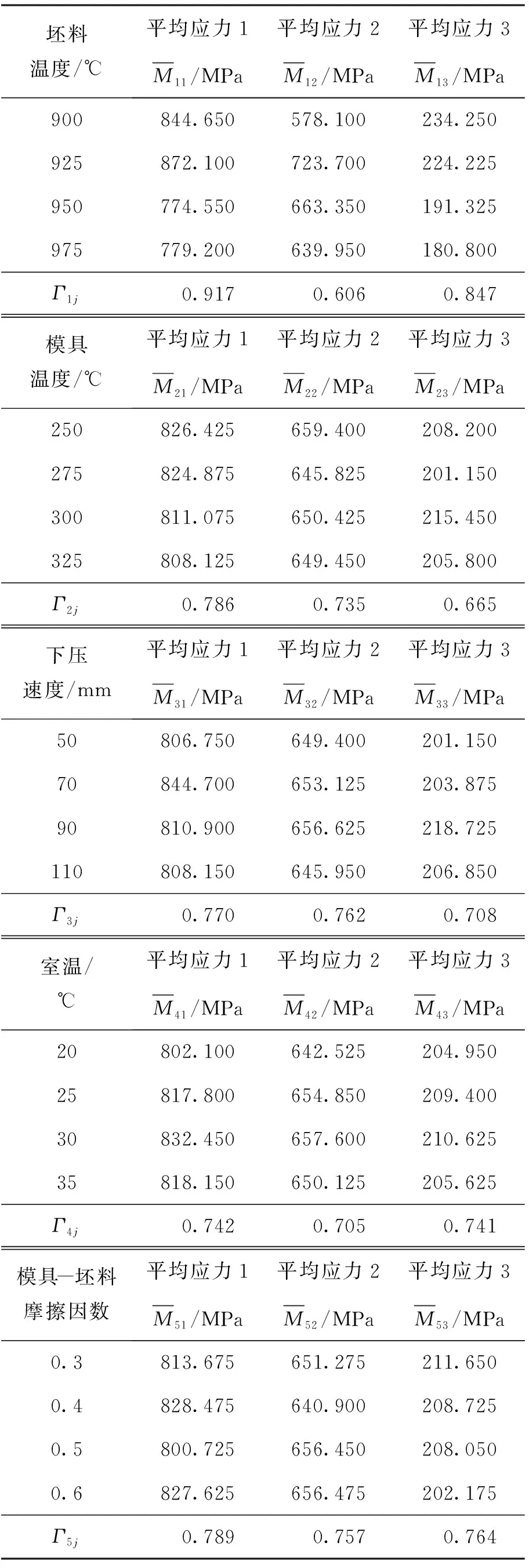
表5 因素灰关联度结果

分析结果如表6所示，综合考虑灰关联程度后发现ξ1>ξ5>ξ3>ξ2>ξ4，所以在锻造过程中坯料初始温度对锻件应力影响较大. 当锻件等效应力较大时可以依次考虑调整坯料温度、模具- 坯料摩擦、下压速度、模具温度、室温，实现质量控制.

表6 相关系数表

2 基于主成分分析方法的等效应力综合评价模型建立

为综合考虑锻件的等效应力情况，应用主成分分析法对应力指标进行综合评价模型建立. 主成分分析方法是多指标综合评价的方法，为降低数据运算量且保存数据信息，将高维指标数据进行降维处理转化实现数据信息简化，再经过方差分析确定权重得到综合评价函数[15-16]. 主成分应力综合指标模型建立步骤如下.

1) 设应力矩阵M=(mij)n×p(i=1,2,3,…,n;j=1,2,3,…p)，其中有n个样本，p类应力指标，对原始应力数据进行标准化处理:

(6)

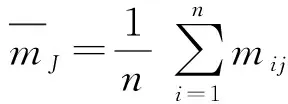
2) 计算应力指标相关系数矩阵R=(rqj)p×p，标准化后的协方差矩阵：

(7)

式中：q=1,2,3…,p;j=1,2,3,…,p.

3) 求相关系数矩阵R特征向量和特征值，由|λE-R|=0计算得到p个特征值，λ1、λ2…,λp，特征值是主成分的方差，特征向量即为载荷因子Lj=(l1j,l2j,…,lpj)T(j=1,2,3,…,p)，各主成分可由载荷因子表示：

(8)

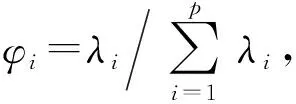
F*=w1Z1+w2Z2+…wkZk

(9)

式中：F*为等效应力综合评价值；w1,w2,…,wk为主成分权重.

表7和表8分别为应力主成分分析结果和载荷因子计算结果. 由表7可以看出M1、M2、M3的贡献率分别为55.62%、35.14%、8.23%，经过降维处理得到Z1、Z2，且新主成分中并未丢失数据信息，同时得到评价模型，基于主成分分析法确定权重分别为0.613、0.387，得到综合指标模型为F*=0.613Z1+0.387Z2.

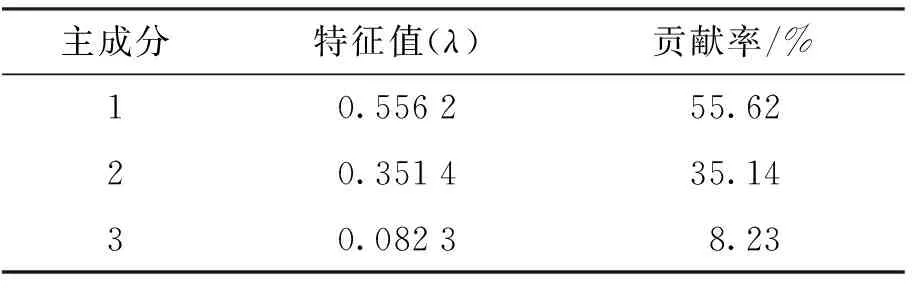
表7 应力主成分分析结果

表8 载荷因子表

当等效应力综合评价值越小时，说明该工件等效应力分布越好.

3 基于BP算法的等效应力预测模型建立与分析

为实现锻造生产过程中锻件质量的综合评价及质量控制，采用前馈误差BP网络，建立综合等效应力评价值与影响因素之间的模型. BP算法通过信息正向传播与信息反向传播不断迭代得到最佳权值、阈值，最终建立输入与输出的映射关系.

BP算法的优势在于能够自适应、自主学习，拥有较强的非线性映射关系，采用非常严谨的链式法则进行误差反向传播过程推导，具有较强的泛化能力[17].

3.1 BP网络模型结构设计

在BP神经网络模型运算过程中，输入层样本向量与权值相乘，输入到隐含层节点中，经过传递函数计算出隐含层向量，再经过输出层激活函数得到输出层各节点的向量组合，最终形成输出向量.

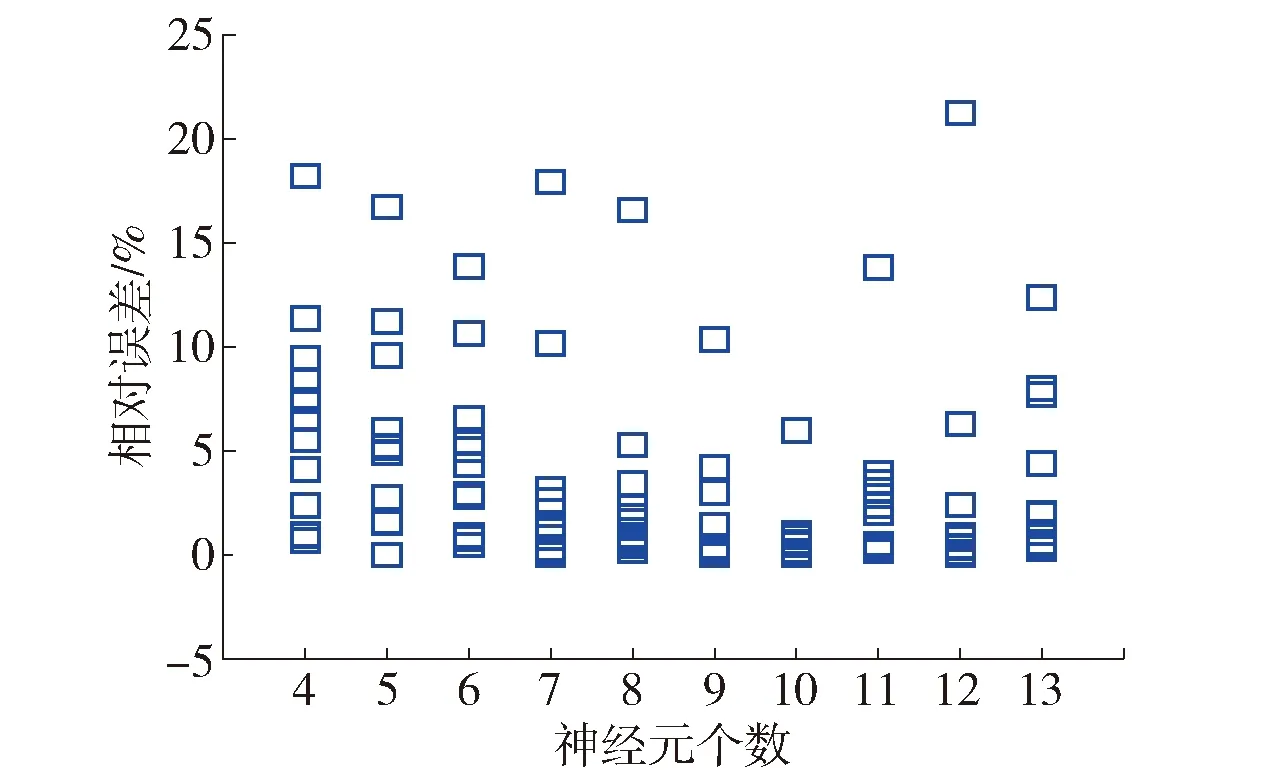
图4 相对误差散点图Fig.4 Relative error scatter plot

3.2 BP网络模型训练

应用正交实验的数据进行BP神经网络训练. 随机选取12组数据作为训练数据[18]，剩余4组作为测试数据. 根据满足误差最小判断条件，当误差小于目标误差时BP网络训练停止，网络训练完成后，如图5及表9可以看出网络模型的相对误差不超过10%，训练数据的仿真实验值和预测值的回归相关性达到0.99，说明网络具有良好的泛化能力.

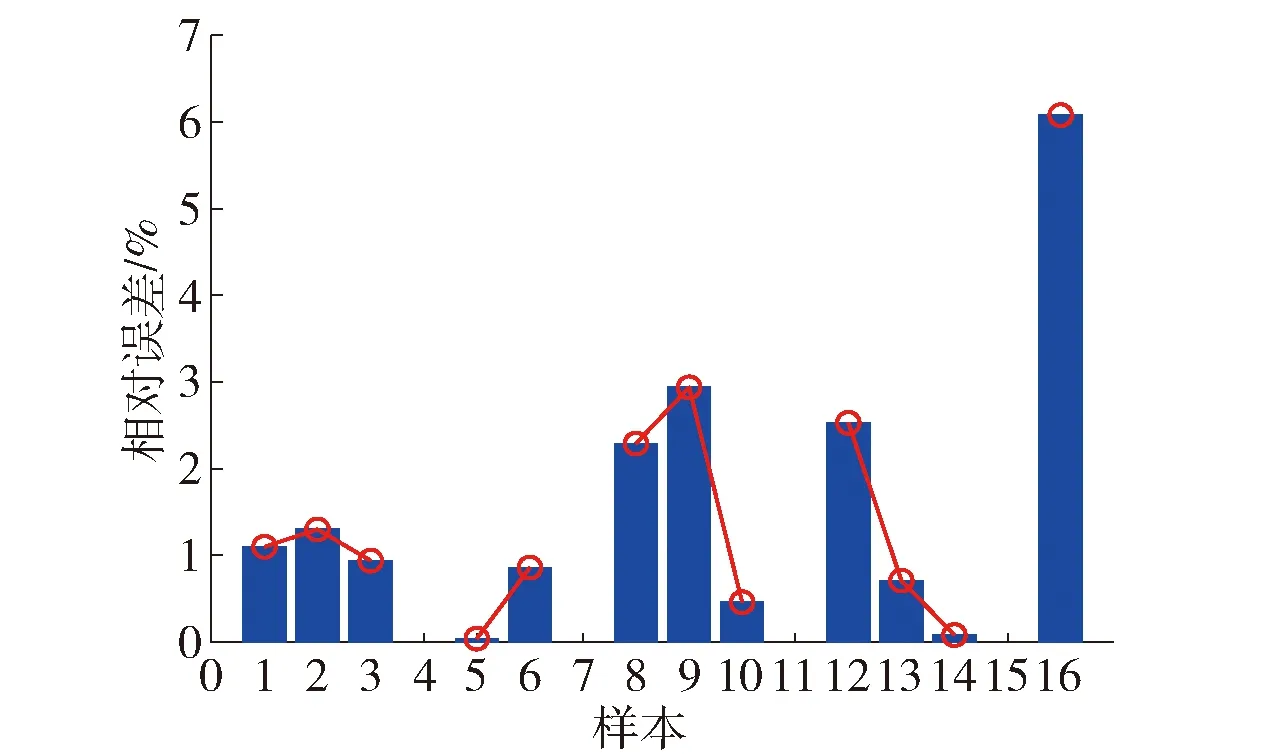
图5 BP神经网络训练相对误差曲线Fig.5 Relative error curve of neural network training

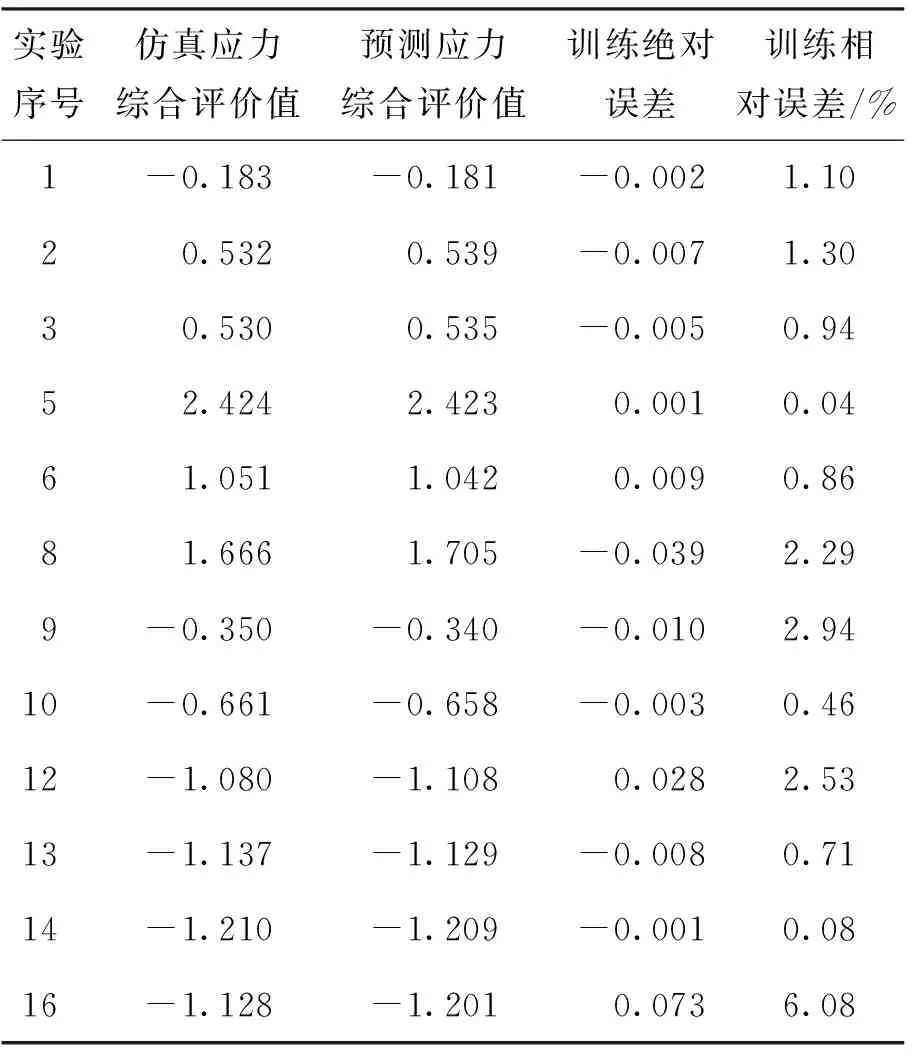
表9 Deform仿真综合应力评价值与BP人工神经网络训练值误差分析

3.3 BP网络模型输出结果与仿真结果对比分析

运用已经建立的BP神经网络对综合应力指标进行预测，选取剩下的4组样本对网络进行测试，网络预测与仿真数据的对比结果可见表10. 从表中可以看出，最大绝对误差不超过0.018，最大相对误差不超过5%，可以看出BP神经网络与仿真结果具有良好的一致性. 因此，该BP网络模型能够精确地描述影响参数、综合应力指标之间的复杂映射关系.

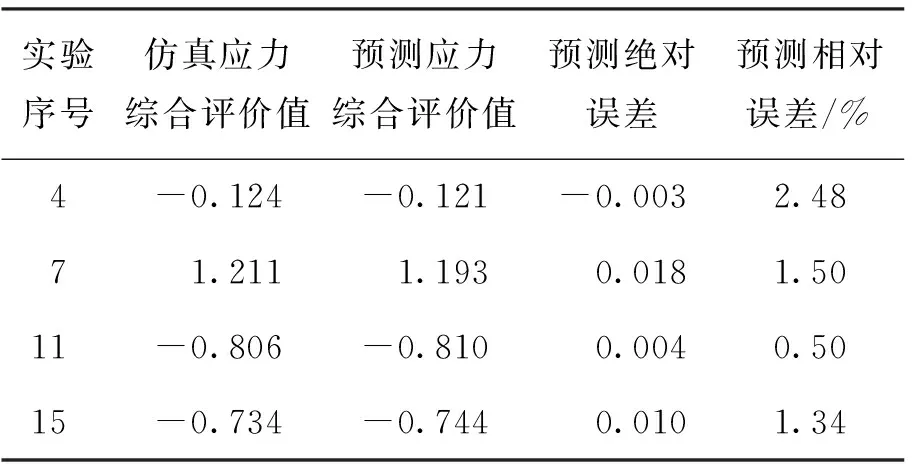
表10 BP人工神经网络预测误差分析

3.4 实验对比验证及分析

本节对4、7、11、15的工艺条件进行了验证，由第2章可知锻件侧表面应力贡献率较大，应用X射线衍射仪对卸载后锻件应力进行应力测试并求均值.

根据4个工艺条件进行锻造实验，表11为预测的综合应力评价值排序，表12为实验测得应力排序，可看出表11、12中预测结果与评价结果较为一致，验证了整体评价与局部评价之间关系的一致性；同时可以看出7号锻件综合评价结果较高，需进一步工艺改进，验证了在线实现神经网络预测锻件应力综合评价值对实际生产具有指导意义.

表11 预测综合应力评价值排序

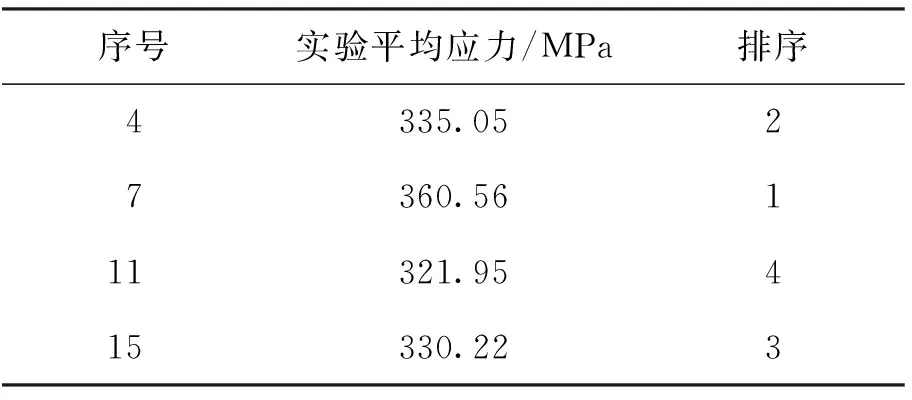
表12 实验应力评价排序

在实际生产中，通过神经网络模型，依据生产过程中的工艺参数实现应力综合评价值的预测，并进行综合应力的评价分析，间接对锻件生产工艺过程进行评价，实现在线锻件质量综合评价预测分析及工艺过程分析，为后续工艺改进及质量控制提供参考依据，提高智能化生产.

4 结论

通过有限元仿真及实验分析了锻件的应力分布规律，基于仿真数据设计了正交实验并分析了影响锻件的因素，建立了综合应力指标；通过BP算法对锻件综合应力指标进行了预测，得出如下结论：

1) 经过仿真及实验可得锻件加载完成后及卸载后的侧表面等效应力较大，心部等效应力较小.

2) 由正交实验数据分析可得影响生产过程中等效应力的最大影响因素为坯料初始温度，最小影响因素为室温.

3) 基于正交实验设计，应用主成分分析法建立了综合应力指标，综合评价模型为F*=0.613Z1+0.387Z2，其中Z1、Z2为主成分分析法降维后的主成分.

4) 利用BP神经网络对等效应力综合评价值进行生产线在线预测. 通过训练、测试及实验验证，预测综合评价值与有限元仿真综合评价值的最大相对误差不超过5%；并进一步经过实验验证，结果显示实验结果与预测评价结果较为一致；为实际生产提供指导，为实现锻造生产在线质量综合评价预测及工艺过程评价分析并最终实现质量控制、工艺改进提供参考依据.