k分搜索的时间复杂度分析
2021-03-08傅晓航郑欢欢
傅晓航,郑欢欢
(南京理工大学 计算机科学与工程学院,江苏 南京 210094)
0 引 言
分治算法是一个将规模较大问题分解为多个规模相同子问题的算法[1]。许多算法都是基于分治策略实现的,例如搜索、快速排序、归并排序、TOP-K算法等等;此外分治策略能够应用于许多算法的优化,例如防火墙规则匹配算法、蚁群算法、并行碰撞检测算法等等,相关研究如文献[2-5]。分治策略的核心思想是将一个问题等分为多个形式相同的子问题,图1所示为每次将问题划分为两个相等子问题时的分治算法。为提高算法的性能,该文将研究将原问题分解为多少个子问题时分治算法的效率最高。

图1 每次划分两子问题的分治算法
该文以搜索为例,搜索是指在一个排好序的数组中寻找与给定数值x相等的元素,很容易想到的方法是将数组遍历,但是遍历的复杂度为O(n),当数组的规模n很大时,查找次数将会很大。
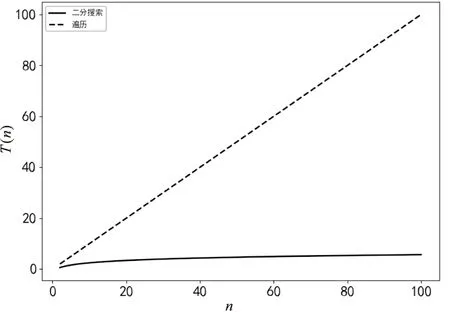
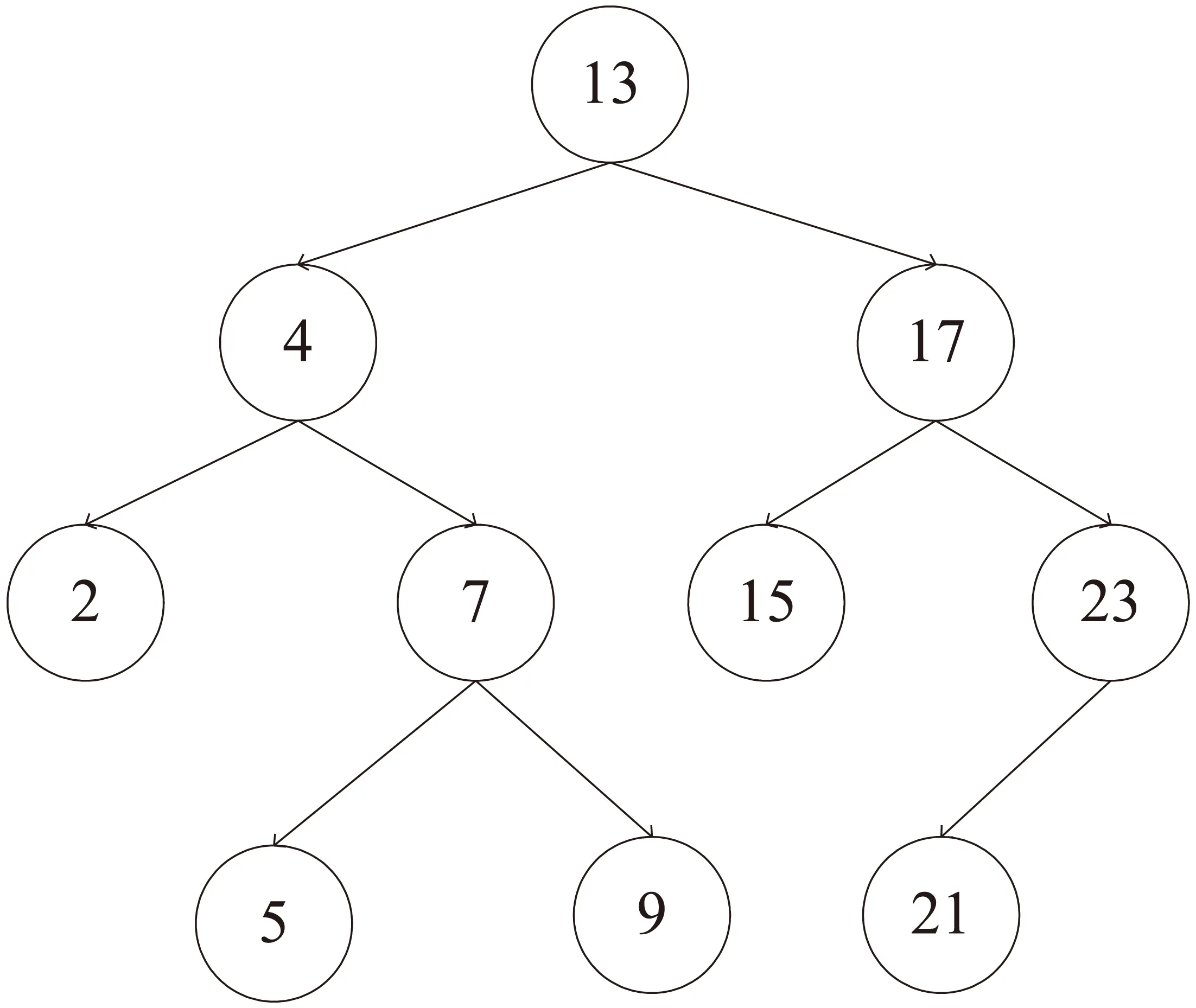
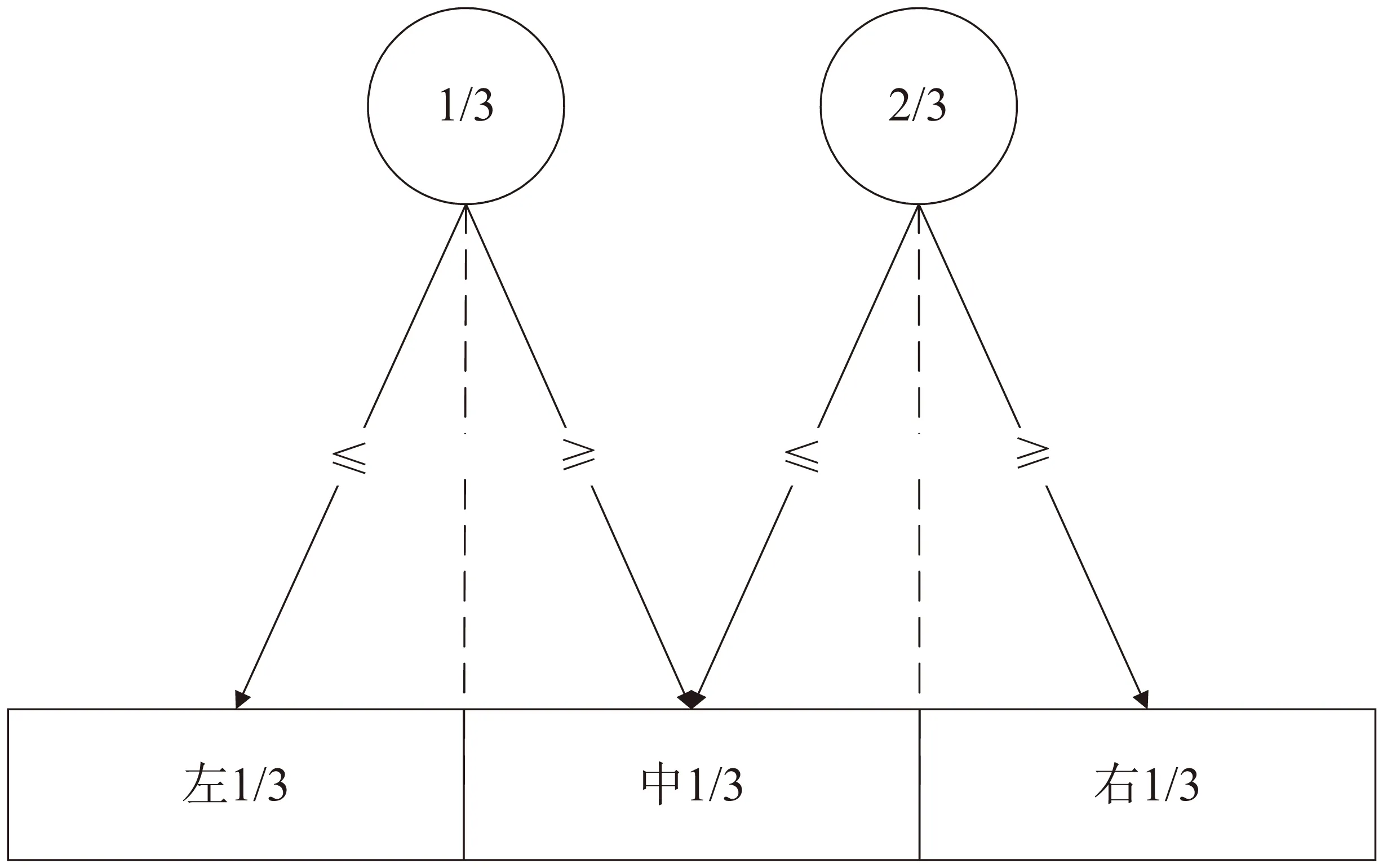
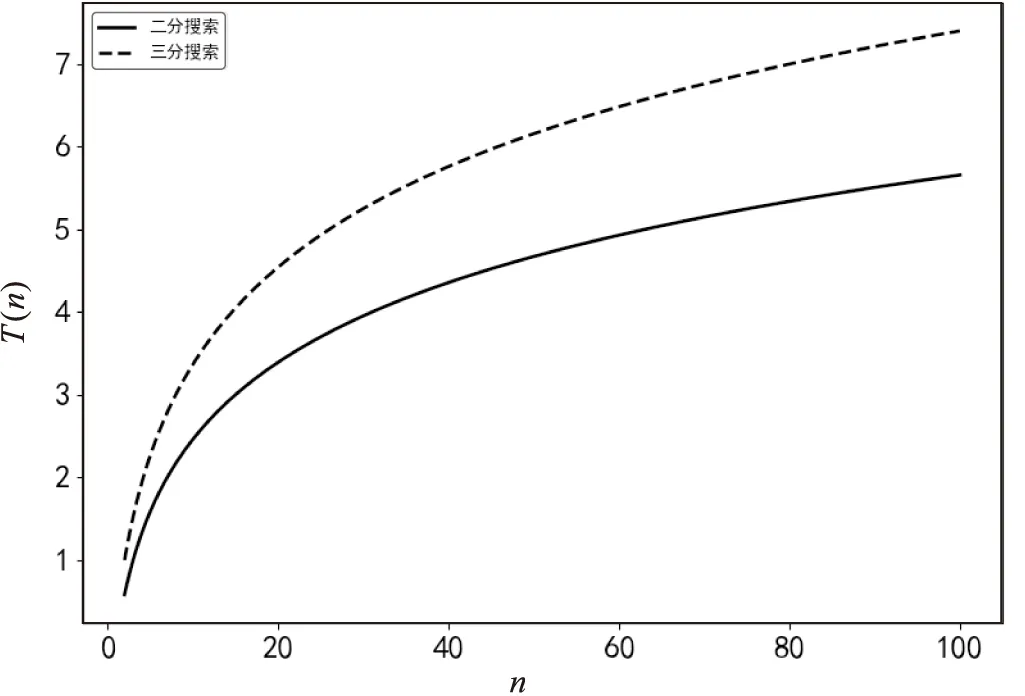
二分搜索是将数组每次分为相等的两部分,将待查元素x与数组中点处的元素a[n/2]比较,若a[n/2]=x则搜索成功;若a[n/2]>x,则待查元素x在数组左半区;若a[n/2] 根据分治策略的研究可以想到,如果每次将数组分为相等的更多部分,比如三部分甚至是k部分,算法性能还会不会有所提升。每次将数组分为更多的部分,则每趟查找能够将数组缩小到更小的范围,然而每趟需要进行额外的查找,从定性分析的角度,总的查找次数增加或减少均是有可能的。随着k的增加,平均查找次数可能先减少,达到最低后再增加;也有可能一直增加,后续将从定量分析的角度,对k分搜索的时间复杂度进行证明。 该文将对二分、三分、四分搜索所需的平均查找次数进行复杂度分析,并进行比较,寻找规律,最后分析出k分搜索的时间复杂度。通过将每种情况下的查找次数求和并平均,得到算法的平均查找次数,进而得到其时间复杂度。可以证明,k分搜索的时间复杂度为O(klogkn),易知klogkn是单调递增函数,因此二分搜索是效率最高的算法。此外,当k=n时,k分搜索退化为遍历,时间复杂度退化为O(n)。 在本节中,首先通过分析平均查找次数的方式分析二分搜索的时间复杂度,然后按照相同的方式分析三分搜索的时间复杂度,最后对比两种算法在实际数据下所需要的查找次数,并分析两者复杂度差异的原因,为寻找k分搜索的规律做铺垫。 258 Analysis of health-related quality of life of elderly people living alone in Shanghai 二分搜索法,是通过不断缩小解可能存在的范围,从而求得问题最优解的方法。二分搜索可应用于二叉搜索树、密度峰聚类、网络拓扑探测等算法,相关研究如文献[6-9]。二叉搜索树的左子树若不为空,则其上的所有节点的值均小于根节点,同样,若右子树不为空,则其上的所有节点的值均大于根节点。二叉搜索树便是利用了二分搜索的性质,既能够快速地查找,又能方便地添加与删除节点,是一种高效的数据结构。 二分搜索能够应用于两种常见的问题中:一是应用于最优解问题,求最小的x使得x满足条件M(x),可以用二分搜索来求得最小的x[10];二是在有序数列中查找值,即在一个排好序的数列中寻找与给定值相等的元素。该文主要通过后者来分析二分搜索的时间复杂度以推出k分搜索的时间复杂度。 社会期望作为一项重要的人格特证,是儿童社会性发展的重要方面,在儿童的成长发展中发挥着不可忽视的作用。儿童的社会期望不仅与儿童的学业成绩和学校表现有着密切关系[3],也会影响儿童对自我的评价[4]和安全依恋的形成[5]。因此,有必要对小学儿童的社会期望水平进行调查,对其发展状况进行系统全面的分析研究,进而为儿童的家庭和学校教育提供可能的参考依据。 二分搜索的方法如图2所示,先将待查元素x与二分之一处的元素比较,若相等,则查找成功;若该元素大于x,则继续在数组左半区查找;若该元素小于x,则继续在数组右半区查找。这样每次都可以将搜索范围缩小一半。 图2 二分搜索的过程 50例ASO患者实验观察指标以SPSS19.0计算。护理工作满意度以%形式展开,采用χ2检验;饮食知识掌握以及护理知识掌握评分以(±s)形式展开,进行t检验。P<0.05证明差异有统计学意义。 1. low←1;high←n;j←0; 2. while(low≤high)and(j=0); 3. mid←(low+high)/2; 2.3 孕晚期血清sFlt-1、PLGF及其比值与子痫前期发病时间的关系 在11例发病的高危孕妇中有早发型子痫前期孕妇2例,晚发型子痫前期孕妇9例。早发型子痫前期组血清log(sFlt-1)的均值为3.82 pg/ml,晚发型组为3.29 pg/ml。血清log(PLGF)的均值在早发型及晚发型子痫前期组中分别为1.83 pg/ml、2.27 pg/ml。血清log(sFlt-1/PLGF)比值在早发型及晚发型子痫前期组中均值分别为1.99、1.01。因早发型子痫前期组孕妇例数过少,数据不符合正态分布,未进行统计学分析。 卞迁与齐薇(卞迁,齐薇等,2009)指出目前最常用的眼动记录方法是无创的视频记录法。利用眼动仪进行研究时测试参数一般包括:注视点轨迹图、热点图、关注区域、注视点个数、首个注视点的注视时长、首次进入AOI的时间、每次访问的平均时间等。一项研究应根据研究内容和研究目标选择2-3个测试参数。 S=(i-1)×2i+1 5. else ifx 6. else low←mid+1; 7. end while; 8. returnj。 要坚持走开放型、创新型和高端化、信息化、绿色化发展的新路子,构建现代产业新体系,从中寻找突破口和切入点,做好产业转型升级的统筹规划,进一步明晰产业转型升级的总体思路、目标任务、方向路径、工作重点和落实机制,扬长避短发挥比较优势,加快推动产业结构由中低端向中高端迈进。推进高原特色农业现代化,促进三大产业融合发展,提高质量效益和竞争力。实施“中国制造2025”云南行动计划,有选择性地承接东部地区出口加工业转移,探索“共建园区”或“飞地经济”,实行引进产业与本地特色有优势产业的有机融合、联动发展。 图3所示为二分查找过程的判定树,要在一个有序数列[2 4 6 9 11 15 18 22 24 31 35]中寻找值为22的元素,首先将22与数组中点处的元素15比较,22大于15,则待查元素在数列右半区;再将其与数列右半区中点处的元素24比较,发现22小于24,则继续在左半区查找;而22大于左半区中点处的元素18,则继续在右半区查找,最终找到22。 图3 二分搜索查找过程的判定树 时间复杂度的分析以分析每个元素被查找到的概率的方式进行。经过1次查找就能被找到的元素个数为20,经过2次查找就能被找到的元素个数为21,以此类推,经过i次查找就能被找到的元素个数为2i-1。设S为所有元素被查找到所需要的总次数,则有: S=1×20+2×21+3×22+…+(i-1)× S=1×30+2×31+3×32+…+(i-1)× (1) 通过错位相减法可以求解式(1),得到: 4. ifx=A[mid] thenj←mid; (2) 由1+2+4+…+2i-1=2i-1≥n,可以得到i≤log2(n+1),代入式(2)可得: S≤(log2(n+1)-1)(n+1)+1 (3) 每个元素被查找到的概率为1/n,则时间复杂度T(n)=S/n,代入得: 11. end while (4) 即二分搜索平均查找次数的时间复杂度为log2(n+1)-1。通过图4可以看出,二分搜索与线性查找相比,时间复杂度由O(n)降到了O(log2n),效率得到了明显的提升。 图4 二分搜索与遍历的时间复杂度的比较 利用二分搜索高效查找的性质,能够将二分搜索应用于一种数据结构即二叉搜索树,又称二分搜索树、二叉排序树,如图5所示。二叉搜索树是一种二叉树,对于树中的每一个节点,若其左子树存在,则根节点的值不小于其左子树中每一个节点的值;若其右子树存在,则根节点的值不大于其右子树中每一个节点的值,二叉搜索树的相关研究如文献[11-14]。若二叉搜索树为满二叉树,则其搜索的时间复杂度为O(log2n),若每层只有一个节点,则复杂度为O(n),因此二叉搜索树的时间复杂度为O(log2n)~O(n)。 (5) 而二分搜索平均仅需20次即可查找成功,极大地提高了算法的性能。 丁珰又道:“天哥他确有过犯,自己送了命也就罢了,最可惜石庄主夫妇这等侠义仁厚之人,却也要赔上两条性命。” 例如,对一个规模为1e6的问题,遍历需要的平均查找次数为: 竖炉密封性较好,通常难以知晓竖炉内部炉墙的实际工况,可使用Raytek手持式红外测温仪检测铜砖部位的温度,且关注超过500 ℃的状况,再根据炉壳发红现象进行综合判断,该测温仪具有响应时间快、非接触、操作简单、使用安全及寿命长等优点。 二分搜索的伪代码如下: 图5 二叉搜索树 二叉搜索树能够做到与线性二分查找一样的时间复杂度O(log2n)。线性二分查找需要保证待查序列是单调的,因此增加或者删除节点时,需要较多的操作;而二分搜索树能够高效地对节点进行增加或者删除操作,是对二分搜索进行优化的一种数据结构。 后续将继续分析,若将问题划分为更多的子问题,即二分搜索、k分搜索,能否更好地提升搜索算法的性能。 三分搜索的方法如图6所示,先将待查元素x与三分之一处的元素比较,然后将x与三分之二处的元素进行比较[15]。若相等,则搜索成功;若x小于第一个元素,则继续在左三分之一部分查找;若x大于第一个元素小于第二个元素,则继续在中间三分之一部分查找;若x大于第二个元素,则继续在右三分之一部分查找。 图6 三分搜索的过程 三分搜索每次能将查找范围缩小三分之一,继续查找,直到找到待查元素x。 现代服装设计中创新应用传统文化元素与艺术价值,第一个必要性体现在,这是现代服装设计创新突破的需要。民族的也是世界的,传统文化为当代的服装设计提供了源源不断的设计思路和设计理念,面对着当前高速发展的时代和服装设计行业的加速更新和变革,行业内部的更新换代以及行业内部的竞争也愈发的激烈,面对这样的现实状况,现代服装设计师在日常工作的过程当中所需要巨大的灵感,而这些灵感则必须是要适应市场的,有可落地实施的价值的,基于这样的现实考量,从传统文化当中吸取营养就显得非常必要。 其伪代码如下: 1. low←1;high←n;j←0; 2. while(low≤high)and(j=0); 3. midl←low+(high-low)/3; 4. midr←low+2(high-low)/3; 5. ifx 由于委派制在某种程度上的“过渡性”和“不彻底性”,审计人员的专业化、系统化的培训较少,人员专业素养提升较慢,难以胜任日益复杂的审计业务要求。 6. else ifx=A[midl] thenj←midl; 7. else; 8. ifx 9. else ifx=A[midl] thenj←midr; 10. else low←midr+1; log2(n+1)-1 12. returnj。 例如对于一个有序数列[2 4 6 9 11 15 18 22 24 31 35 39],寻找与值22相等的元素,首先将22与三分之一处的元素9、三分之二处的元素24比较,易知9<22<24,则继续在中间三分之一部分[11 15 18 22]查找;再分别与11和18比较,发现大于18,则在右三分之一部分查找,最终找到元素22。 时间复杂度的分析方法与二分搜索类似,在查找过程中,第1趟需要找2次,能够被找到的元素有2×30个,第2趟需要找2×2次,能够被找到的元素有2×31个,第i-1趟需要找2×(i-1)次,能够被找到的元素有(i-1)×3i-2个,第i趟需要找2×(i-2)次,能够被找到的元素有i×3i-1个。每个元素被查找到的概率为1/n,则时间复杂度T(n)=4S/n,其中: 2i-2+i×2i-1 3i-2+i×3i-1 (6) 通过与二分搜索相同的方法可以得到: 2log3(n+1)-1 (7) 即三分搜索平均查找次数的时间复杂度为2log3(n+1)-1。 由1.1节和1.2节可知二分搜索的时间复杂度为log2(n+1)-1,三分搜索的时间复杂度为2log3(n+1)-1,易知log2(n+1)-1<2log3(n+1)-1,故二分搜索的效率更高。图7为随着数组规模n的增长,两者时间复杂度的比较。 图7 二分与三分搜索时间复杂度的比较 表1为在实际数据下,分别使用规模为100、1 000、10 000、100 000的数组,二分搜索与三分搜索所需的查找次数。虽然有个别情况三分所需次数更少,这是因为被查找的位置恰好在三分点上,但从总体上看,还是二分所需次数更好。 表1 二分与三分搜索在实际数据下的比较 无论是从平均查找次数的复杂度分析还是通过实例分析都可以看出二分搜索比三分搜索的效率更高。与二分搜索相比,三分搜索虽然每次将待查数组缩小到更小的范围,但是二分搜索每趟只需要查找一次,即中点处的元素,而三分搜索需要两次,即三分之一与三分之二处的元素,每趟搜索就增加了一次查找,随着搜索次数的增加,三分搜索所需要的额外查找次数越来越多。因此,三分搜索与二分搜索相比,平均查找总次数更多,时间复杂度更高。 为了找出k分搜索的复杂度,首先分析四分搜索以找出规律,分析方式同上,可以得出: 中国现代民俗学大致经历了从事象研究到事件研究的范式转换,但这是远远不够的,王霄冰从民众群体(民)与知识体系(俗)之间的关系入手,提倡关注“民俗事件中的社会关系”,这相比“语境中的民俗”的提法而言指向更加明确。不过还应注意的是,“熟人社会”内部借助民俗活动对已有社会关系的刷新或调整,与“生人社会”借助民俗活动而达成的开放式的社会关系,虽然都属于多主体之间的民俗关系,但其差异甚为明显,加以区别是必要的。民俗在“熟人社会”与“生人社会”所承担的不同角色,启发我们应在更广泛的社会视野中体认民俗。 (8) 则时间复杂度为: 3log4(n+1)-1 m_Server.CertificateEvent += new certificateValidation(m_Server_CertificateEvent);//定义服务证书 (9) 可以看出,四分搜索与三分搜索相比,时间复杂度再一次增加,据此推测,k分搜索的时间复杂度是随着k的增加而增加的,以下过程证明了这一点。 对于k分搜索有: (10) 时间复杂度为: (11) 上式可近似为(k-1)logk(n+1)-1,随着k的变化,时间复杂度的变化如图8所示。 图8 随着k的升高k分搜索时间复杂度的变化 可以看出时间复杂度T是随着k的增加而增加的,因此二分搜索的效率是最高的。虽然k分搜索每次能将搜索范围减小到原来的1/k,即公式中的logk,但是每趟搜索需要查找k次,即公式中的系数k,因此,随着k的增加,需要的查找次数也越来越多,因此时间复杂度也是增加的。 因此,各种算法如快速排序、极限情况,当k=n时即为遍历。此时每次将搜索范围缩小为1/n,只需一趟搜索,但是需要搜索n-1次,即与前n-1个元素均要进行比较,如图9所示,与遍历的方式是相同的。 针对在地下水取水井专项普查数据中不易获得的数据,如机电井的打井时间、打井深度、水位埋深、水泵的各项指标数据及动态数据等,勃利县采取了以下几种方法获取: 图9 n分搜索 时间复杂度为: (12) 如图10所示,n分搜索与遍历的复杂度n是十分接近或者说近似相同的。 图10 遍历与n分搜索的时间复杂度的比较 通过一系列的分析与证明,研究了二分、三分、k分搜索的时间复杂度,得出如下结论:(1)证明了k分搜索的时间复杂度是O(klogkn); (2)二分搜索是效率最高的搜索算法,对于k分搜索来说,k越大,算法效率越低。虽然三分、k分搜索与二分搜索相比每次查找能将待查找数组缩小到更小的范围,但是二分搜索每趟只需要查找一次,三分搜索需要两次,k分搜索需要k-1次,这就增加了查找次数,使得时间复杂度升高;(3)当k=n时,k分搜索退化为遍历,时间复杂度退化为O(n)。1 二分搜索与三分搜索
1.1 二分搜索



1.2 三分搜索

1.3 二分搜索与三分搜索的比较
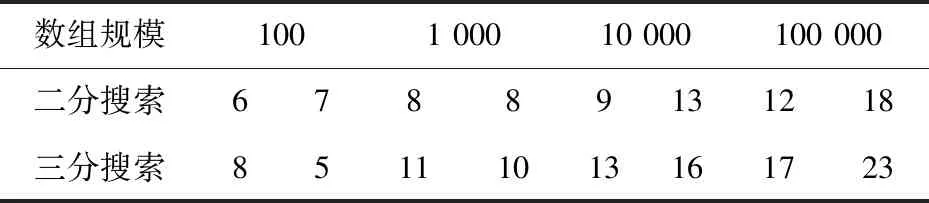
2 k分搜索
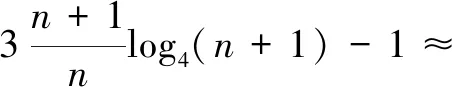
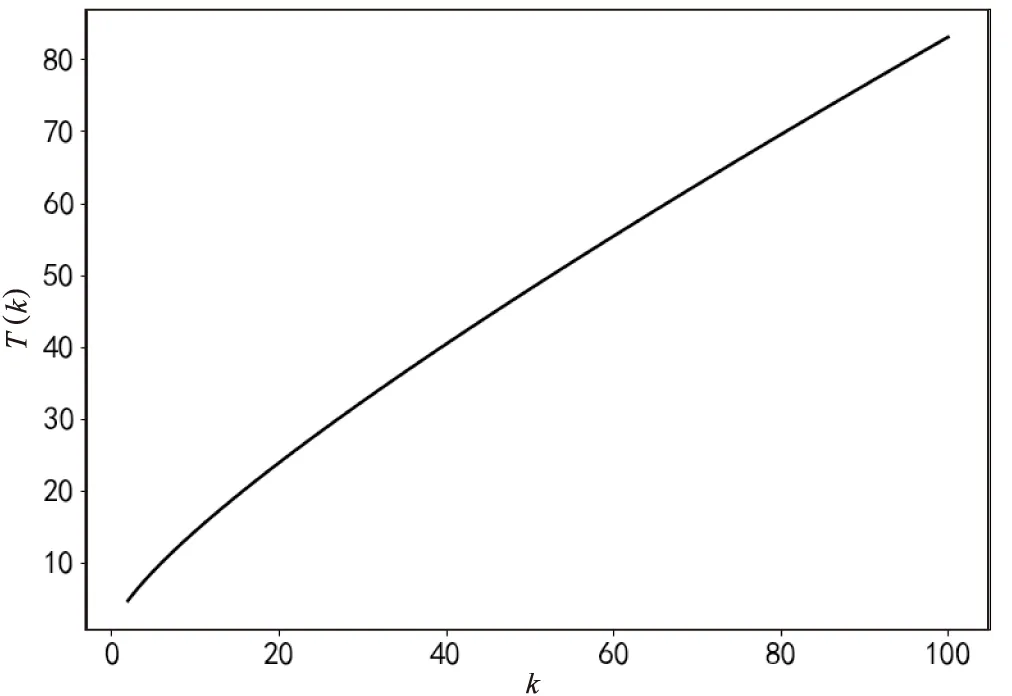


3 结束语
