基于自组织神经网络在油气分层中的研究

冯向东，张玉琴，韩红伟，张建亮

(成都理工大学 工程技术学院，四川 乐山 614007)

0 引 言

地球物理曲线的分层研究对勘探和开发油气资源是一种重要手段，是在认识油气层的地质面貌和剖析油气藏量的内在规律等方面的一种较为有力的武器。测井的第一步就是需要利用各种各样的仪器与设备，来对各种岩层中所含的物理参数进行测量，例如放射性、导电性、以及声学特性等，第二步则需要对测井曲线进行研究与分析，从而可以较好地得到岩性信息与地质信息[1]。现阶段较为常用的测井方法有放射测井、成像测井、电测井和声波测井等等，其所得到的各种参数结果，从某一侧面都能够反映相应的地质特性。当然，假如想对地质的构造及变化进行全面的研究，那么就必须综合多种测井参数。

测井曲线的层序划分在油井勘测开发中必不可少，在对地层进行划分、对地层的岩性进行判别、对储层进行预测等方面都具有非常重要的意义。长期以来，在进行地质分层时，不仅仅考虑曲线的形态，还需要根据曲线反映的各种信息通过分层人员丰富的知识来获得最优解，可是这不仅需要具备丰富的知识积累和熟练程度，而且费时费力，主观性还很强，并且由于没有一个统一的分层准则，每个人都使用自己的分层方式，导致结果的差异性过大，出错率也较高。而与人工分层相比，自动分层不仅可以规避人为分层的随意性，还可以较大程度地提高工作效率并且避免一定的失误率[2]。

现阶段，通过测井曲线来进行地质面貌的分析时，主要方法还是按照层来进行分析的，因此第一步就必须完成曲线的分层分析。由于每个物理层的地质特征应该是相似或者相同的，因此首先可以通过相似的曲线来把剖面划分成若干个小层。这样做的目的，不仅可以有效降低非地层因素的干扰，同时也可以突出地层与地层中所拥有的流体物质的变化，进而大大地提高了解释的精度。在过去较长的一段时间里，基本上都是测井人员人工先对曲线的形态变化进行观察，再依据自身所积累的经验来找出曲线中每一段所含有的半幅点位置，用来划分地层。显然由于测井人员自身所积累的经验的高低，以及熟练程度的差异，其所得到的分层结果必然会有特别大的误差，最终导致了准确率的降低。

随着计算机技术逐步应用到测井的解释中，自动分层技术[3-5]也获得了较快的发展，不仅减少了以往那些人工解释中含有的人为因素所造成的分层误差，同时大大提高了工作效率。现有的利用曲线来自动划分地层的方法，按照数学分类的准则主要是数理统计方法和非数理统计方法，以及人工智能算法[2]。而这些数学方法也都各有优缺点。

数理统计方法主要有方差分析法、聚类分析法[6-11]等，但如果在细致分层时使用这种方法，其计算量将会非常大，普通的家用计算机根本无法承受这样的计算量。非数理统计方法是以小波变换方法[12-13]和活度函数法为主。人工智能算法主要还是使用BP神经网络[14-17]，可是如果使用神经网络并且想要保证分类结果的正确性，就需要有大量的样本才能实现，同时还有可能会陷入局部最优解，因此其分类结果有较大的可能性会存在误差。

另外，大量的支持向量机改进算法[18-20]被用于分类，同时支持向量机在测井解释中的应用[21-22]也被陆续提出，但所需的分类问题中应该是大量的多分类问题，而支持向量机本身其实是二类的分类算法，所以如果利用支持向量机来处理多分类问题，这将是一个需要值得深入进行研究的课题。

针对聚类分析和BP神经网络算法存在的问题，通常采用的做法是主成分分析降维或者是选取有代表性的几条曲线来实现。但是无论哪一种做法，都会使得有用信息缺失，造成分层错误。该文将结合自组织神经网络，来对油气层的识别进行数据的分析。

1 测井数据的预处理

在收集的某地区测井数据中，首先在采用放射测井时，可能会遭受到来自核外电子、核衰变、伽马量子等方面的随机作用，许多与地质特性根本没有关系的起伏变化会出现在测得的曲线上；同时，由于声波会经过多次的折射与反射、测井探头会遭到随机碰撞等原因，曲线上必将出现大量带有毛刺的干扰。显然如果在进行测井解释时，直接使用这些带有干扰的曲线来进行，其分类的结果必然会含有很大的误差。以自然伽玛数据为例，见图1。所检测的7 482个数据中，有375个异常数据点。

图1 原始数据

因此对于这些与地质无关信息的干扰，必须设法滤除；同时曲线上能反映地质特性的有用成分，也必须最大限度地保留。通常出现这样的情况，不少工作人员会采取去除异常点或者前后两点取平均值的方法来解决。但这样无形中给自动分层加入了人为因素。

由于同一层物质的连续性，因此同一指标应该是连续变化的，采用三次样条插值的方法进行测井曲线平滑处理，修正以后的数据曲线见图2。同时也为后续地层划分和测井分析提供了正确、有力的数据支持。

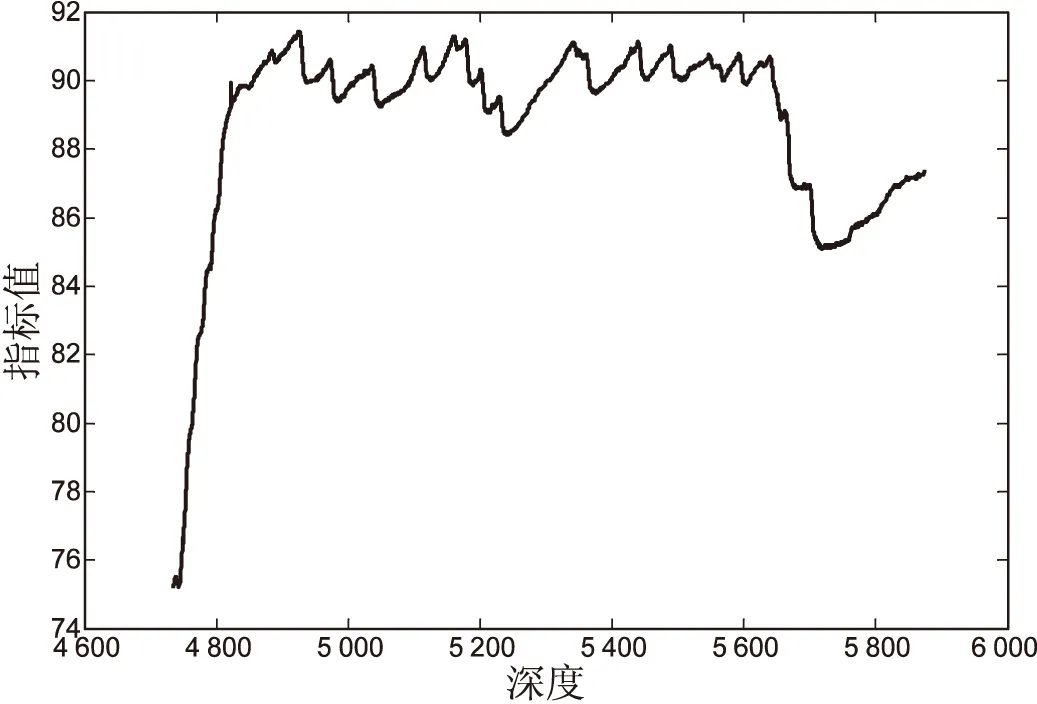
图2 修正以后的数据

2 自组织神经网络

自组织神经网络算法是一种在没有监督学习的状态下神经网络映射的过程，它是通过神经元之间的相互竞争与学习来完成的。在整个学习的过程中只需存在有一些学习的样本，而不用去提供理想的目标与输出。通过输入样本的特征，该网络会自组织地进行映射，同时对训练的样本进行自动分类[23-25]。自组织神经网络主要是由输入层与竞争层所构成。在模式识别问题中，该网络的输入向量是能反映油气模式的训练样本，在训练网络的过程中，权值向量与输入向量中，谁最接近神经元，就会在竞争中最终获胜。当然该神经网络也会根据自身的学习规则，及时对这个获胜的神经元进行权值的调整，获胜神经元的权值向量在修改后，也能够更加接近当前的输入向量。最终可以将任意维的输入向量，变换到一维或二维离散的网络上，同时保持一定的拓扑有序性。

(1)

其次就是需要确定最佳匹配单元的领域，该领域是随迭代次数n的变化而变化的，故称此为领域函数Λi(n)。当然，这里还需要一个在Λi(n)内的单元例能够修改权值的公式。为此将加入一个遗忘项—g(yj)wj，其中g(yj)是单元j的输出的非负的标量函数，而且满足：

yj=0，g(yj)=0，∀j

(2)

这样，用微分方程来表示权值的学习：

(3)

网络的学习目的，就是在最佳的匹配单元周围形成一定的“气鼓”，在这里选取：

(4)

由式(2)，有：

(5)

带入式(3)，有：

(6)

为了进一步简化，取α=η，η为学习步长，则式(6)变为：

(7)

对离散的情况：

wj(n+1)=

(8)

SOM算法的步骤大致可以归纳如下，主要由竞争过程、协作过程和自适应调整过程组成：

Step1：初始化权值向量，选用较小的随机数对各个权值向量赋初值wj(0)，而各个节点的权值必须取为不同的值。

Step2：在样本集合中任意选取一个样本x作为输入向量。

Step3：在时刻n，选取最佳的匹配单元i，即：

Step4：确定领域函数Λi(n)。

Step5：修正权值

wj(n+1)=

Step6：n←n+1，返回Step2，直到形成有意义的映射图。

3 研究实例分析

在分析数据过程中，需要结合工程应用中的实际需要来对指标进行筛选。在某地区的3号井中，选取了自然伽马(GR)、声波时差(AC)、密度(DEN)、深侧向(RLLD)、微球形状聚焦(RMSF)等19个指标，共计7 478×19个数据。以水层、油层、油水同层和干层等四种层位进行研究。

3.1 原始数据的计算

按照前面提到的算法步骤，采用自己编写的MATLAB程序：

clc,clear,

A=load('shujuLG022.txt');

X=A';

[n,p]=size(X);

m=4;%要求输出4个神经元

K=5 000;% 最大训练次数

a=0.5;%初始比例系数

a1=min(A);a2=max(A); A1=repmat(a1',1,m);A2=repmat(a2',1,m);

W=unifrnd(A1,A2);%随机产生权值

for k=1:K

r=floor(5*(K-k)/K);%修改邻域半径

b=a*(K-k)/K;%修改比例系数

for t=1:p

for j=1:m

Y(j)=norm(X(:,t)-W(:,j));

end

i=find(Y==min(Y));

i=i(1);%寻找获胜单元

for j=1:m

if abs(j-i)<=r

W(:,j)=W(:,j)+b*(X(:,t)-W(:,j));%修改权值

end,

end,

end,

end

W

for i=1:p

c=X(:,i);

CC=repmat(c,1,m);

AA=CC-W;

SSS=sqrt(sum(AA.^2));

k=find(SSS==min(SSS));

T(i)=k;

end

T

经过计算，7 478个数据的分层结果中，在四种层位分别所占比重见图3。油水同层所占比重最小，只占到3%，水层次之，有16%，而油层最多，占到了41%。并从中选出10个原始数据的分类结果，放在表1里。

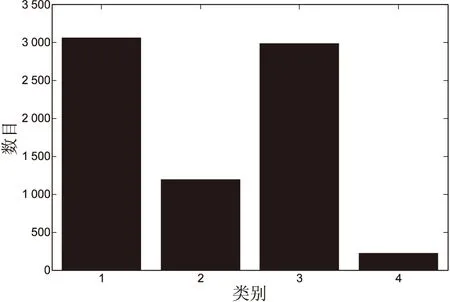
图3 各层在原始数据中所占的比重

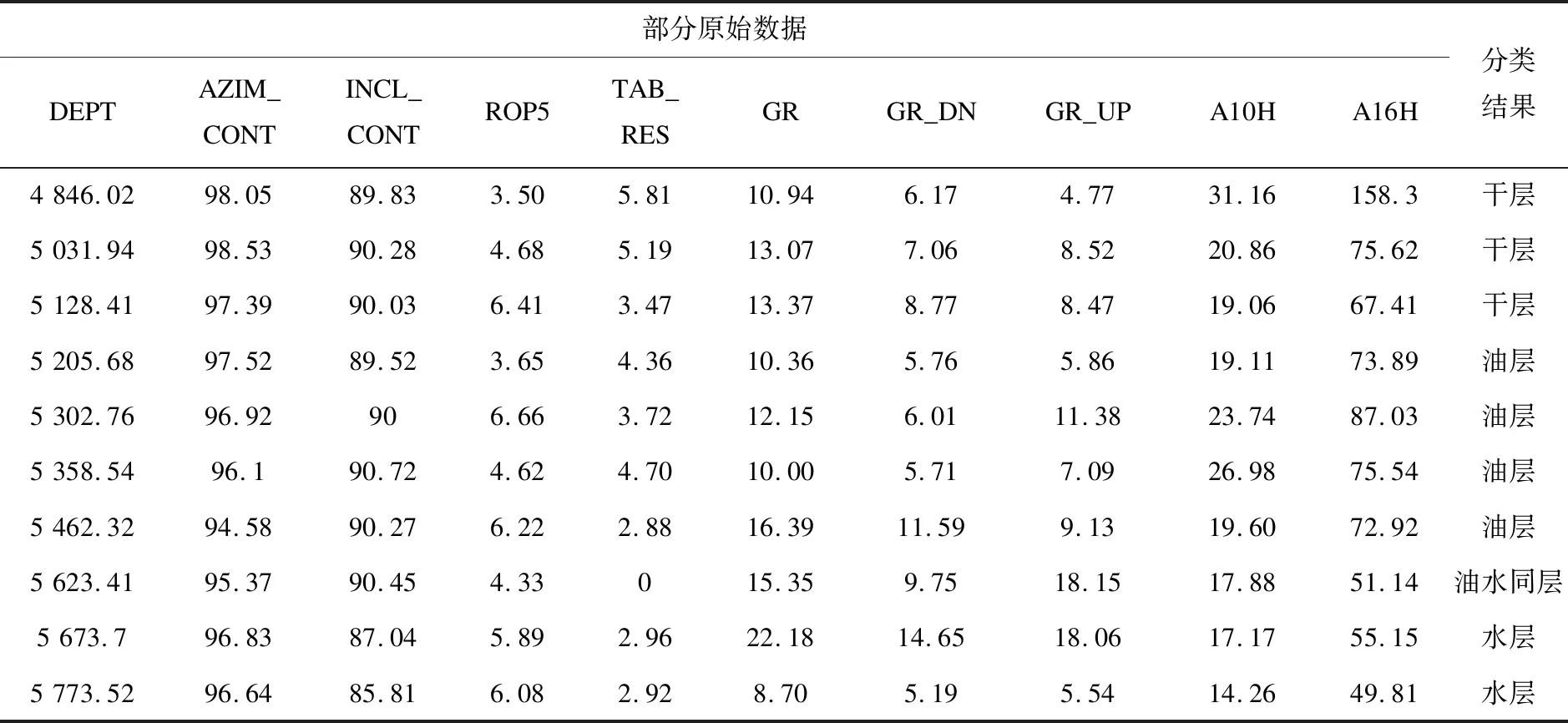
表1 部分数据的分类结果

3.2 结果检验

为了验证以上分类结果的正确性，就需要对各层的物性及含油性进行评价，同时掌握各层中不同曲线所能展示出来的不同特征。

油层的特征包括微电极的曲线幅度中等，带有明显的正幅度差，如果渗透性变差则幅度差将会变小；自然电位曲线会显示出正异常或负异常，伴随泥质含量的增加其异常幅度随之变小；长、短电极将视电阻率曲线呈现有高阻的特征；感应曲线显示出明显的低电导；而声波的时差值处于中等，曲线平缓也将呈现平台状。

油水层的特征有微电极曲线幅度处于中等，正幅度差明显，但若与油层相比较，其幅度会相对降低；自然电位曲线同样显示有正负异常，但异常幅度值将会比油层要大；短电极视电阻率曲线的幅度较高，但是长电极视电阻率曲线幅度将会较低，高电导值会显示在感应曲线中；声波的时差数值同样处于中等，且呈现平台状，而井径通常会小于钻头的直径。

干层的特征为极浅电阻率曲线幅度处于中等，带有明显的正幅度差；若与油水层比，其幅度又会再次降低；自然电位曲线和油水层一样，展现出正异常或负异常，但其异常幅度值会比油水层大；在声波的时差曲线中，伴有明显的数值增大、周波跳跃的现象，而中子伽玛的曲线幅度比油层更高。

水层呈现有极浅电阻率，曲线幅度中等，正幅度差明显，其幅度比油层要低；自然电位曲线依然会显示有正负异常，而异常的幅度值比油层要大。

以人工分层准则的结果作为标准，自组织神经网络算法所的结果，准确率达到82.17%。说明自组织神经网络算法基本上满足分层的要求，能够较为成功地识别该组数据，并且利用计算机所花时间大大少于人工分层所用时间。

4 结束语

该文主要是通过采用自组织神经网络来对油气数据的分层应用进行聚类研究。通过自己编写的MATLAB程序算法对网络进行优化设计和处理，并将测井的数据和最终的数据处理结果，都放在了同样的一个系统之中，使其能够自动完成测井数据和得到油气分层识别之间的一个高度映射关系，充分反映出输入的测井曲线信号特征和油气层之间的内在联系，为油气层网络的自动识别创造了条件。而在数据输入初期，通过插值的方式，消除该测井数据随机干扰带来的噪声，同时也保留了数据的完整性和代表性；最后，与该地区的地质资料进行对比，结合人工分层的结果加以验证，以保证利用自组织神经网络识别的结果能够更加客观和可靠。

研究结果表明，采用自组织神经网络进行油气层识别是可行的，该方法的可操作性强，原理简单易于实现，参数与网络结构容易调整，识别率比较高，是研究测井曲线的一种有效的手段。该方法不仅能够对国内现有的油气田进行油气层的识别，还可以对原有的旧井进行再次复查，以便能够发现是否存在新的油气层位，提高油气产量。

当然，该方法仅仅是在数据分析基础上建立的，没有能够结合地质学中相关的知识。从最后与人工分层的结果验证来看，如果在此算法的基础之上，能够再依据地质学中的专业知识，那么将是对测井曲线进行了更加科学的分析，也必将得到更加合理的分层结果。