面向区块链的在线联邦增量学习算法

罗长银，陈学斌*，马春地，王君宇

（1.华北理工大学理学院，河北唐山 063210；2.河北省数据科学与应用重点实验室（华北理工大学），河北唐山 063210；3.唐山市数据科学重点实验室（华北理工大学），河北唐山 063210）

（*通信作者电子邮箱chxb@qq.com）

0 引言

谷歌于2016 年提出了一种新兴的隐私保护技术——联邦学习［1］，因其具有保护隐私和本地数据安全的优势，被广泛应用于多个领域。

联邦学习可以应用至金融领域，如杨强教授团队将联邦学习应用在小额信贷的风险管理、反洗钱等案例中［2］；联邦学习还可应用于语音识别，如：保险客服的语音识别与质量检测的语音识别，采用联邦学习的框架建立二者共享的语音识别（Automatic Speech Recognition，ASR）模型，并取得了很好的收益。

联邦学习的训练数据来源于不同数据源，导致训练数据的分布与数量成为影响联邦模型的条件。若数据源的训练数据分布不同，那么整合多方本地模型就成为难题。文献［3］使用Logistic 回归模型作为初始全局模型对各数据源的数据进行训练，采用神经网络来整合本地模型；但神经网络模型的表现为非凸函数，很难使参数平均化后的模型损失函数［4］达到最优。针对此问题，文献［5］中提出了联邦平均算法FedAvg，采用权重或梯度的平均值来整合多方本地模型后获得整合的全局模型。但文献［6］针对联邦平均算法FedAvg 提出了深度梯度泄漏算法，能够根据本地模型的梯度更新还原出大部分训练数据。同时，上述文献均没有考虑联邦模型时效性的问题。

针对数据安全性与模型时效性问题，本文提出了一种面向区块链的在线联邦增量学习算法。该算法利用集成学习的思想来整合多方本地模型，以训练出多方都满足的全局模型。训练结果表明，该算法的准确度比传统整合数据训练模型的方法略有降低，但数据与模型在训练模型阶段的安全性得到提升；同时相较一般联邦学习模型，该算法可以将每个时间段、每次迭代的参数与结果自动上传至对应的数据块中并快速同步，数据传输成本大大降低；而且因区块链数据不可篡改与不可删除的特点，使模型在存储阶段拥有双重保障敏感数据的安全性。

1 相关知识

1.1 区块链

区块链的概念在文献［7］中首次提出，是分布式数据存储、点对点传输、共识机制、加密算法、时间戳、哈希算法以及相关计算机技术组成互联网时代的创新应用模式。

区块链因其具有去中心化、数据不可篡改、数据安全可靠与可溯源以及集体维护的优势，所以被广泛应用。例如：文献［8］利用区块链去中心化的特点，提出了基于区块链的电子健康记录安全存储模型。

区块链由多个区块连接而成，它利用哈希算法对每个数据区块的头部进行运算可以得到一个哈希值，使用这个哈希值可以将区块之间连接起来构成一条链，此为区块链结构的本质。数据区块当中记录了当前时间下的交易信息，采用默克尔树信息进行保存。每一个数据区块由区块头与区块体组成，数据区块的结构如图1所示。

1.2 RSA加密算法

RSA 加 密 算 法 是Ron Rivest、Adi Shamir 和Leonard Adleman 三人于1977 年在文献中首次提出［9］，因其是一种非对称加密算法，所以在公开密钥加密和电子商业中被广泛应用。例如：文献［10］提出的基于强认证技术的会话初始协议安全认证模型使用RSA 数字签名来保证消息传输的机密性、真实性、完整性和不可否认性。

1.3 椭圆曲线数字签名算法

椭圆曲线数字签名算法（Elliptic Curve Digital Signature Algorithm，ECDSA）［11］是使用椭圆曲线加密（Elliptic Curve Cryptography，ECC）算法对DSA（Digital Signature Algorithm）的模拟，在2000年成为IEEE和NIST的标准，具有生成的密钥长度短而且签名和验证速度更快，在具有相同安全性的情况下，所需的存储资源更少的优点，因此被广泛应用。

图1 区块链结构示意图Fig.1 Schematic diagram of blockchain structure

1.4 联邦学习

联邦学习是隐私保护下的算法优化可实现路径和保护数据安全的“数据孤岛”问题的解决方案［12］。具体实现过程为：对多个参与方在本地私有数据上进行模型训练，然后将不同的模型参数上传到云端进行整合和更新，之后将更新的参数发送至各参与方。整个过程私有数据不出本地，既保证了数据隐私，同时解决了各参与方“数据孤岛”的困境，根据其实现过程使得联邦同样具有联邦学习保护隐私和本地数据安全的优势。

1.5 集成学习

在有监督学习算法［13］中，训练出的模型在满足稳定性的同时还要求模型各方面的性能都较好，但实际情况是有时只能得到多个有所偏好的模型（弱监督模型［14］）。集成学习［15］就是将多个弱监督模型组合成一个更好、更全面的强监督模型，集成学习的思想是即使某一个弱分类器得到了错误的预测，其他的弱分类器也可以将错误纠正回来。在集成学习中，stacking 集成是目前提升机器学习性能最有效的方法［16-18］。从图2 中可以看出，stacking 集成分为两步：1）使用多个算法求出结果；2）将结果作为特征输入到下一个算法中训练出最终的预测结果［19-21］。

图2 stacking集成示意图Fig.2 Schematic diagram of stacking ensemble

2 在线联邦增量学习算法

2.1 算法描述

在线联邦增量学习算法是在联邦学习的框架与集成学习的思想下建立的，图3为该算法的整体框架。从图3中可以看出，该算法包括数据收集阶段、模型训练阶段和模型存储阶段三个阶段。在数据收集阶段使用数字签名来保证数据的安全性与完整性；在训练模型阶段采用联邦学习框架与增量学习算法，保证了数据的安全性与模型的时效性；在模型存储阶段，采用区块链来存储每个时间段内各模型的参数，使数据传输成本大大降低，同时使数据的安全性得到保障。

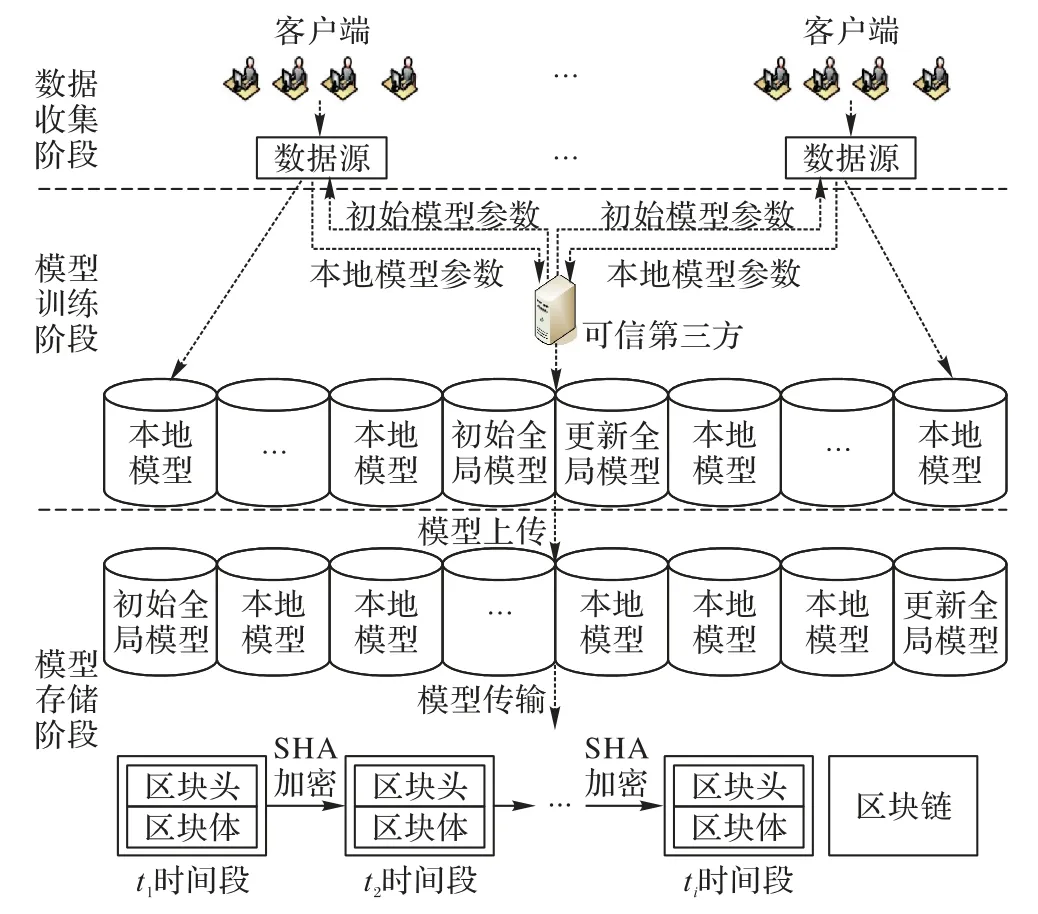
图3 基于区块链的联邦增量学习算法的整体框架Fig.3 Overall framework of federated incremental learning algorithm based on blockchain

数据收集阶段的算法如图4 所示，具体流程如下：1）各客户端需要计算数据的hash 值，并使用由RSA 加密算法产生的公钥来加密hash 值，再传输至各数据源。2）各数据源使用私钥解密，并重新计算数据的hash 值。3）判断解密得到的hash值与重新计算的hash 值是否相等：若相等，需要将数据存储到数据源中，等待模型训练；若不相等，表明此客户端的数据在传输过程中被篡改，以此可保证数据收集阶段数据的安全性与完整性。

模型训练阶段的算法如图5 所示，具体流程如下：1）由可信第三方使用RSA 加密算法将初始全局模型传输至各数据源，保证模型安全性；2）各数据源将解密的初始全局模型在历史数据与增量数据上进行训练，获得每个时间段内的本地模型；3）将本地模型传输可信第三方，可信第三方使用stacking集成算法来整合多个本地模型，获得每个时间段更新的全局模型，且不断迭代训练。其中，该阶段训练模型的公式如下：

初始全局模型分为三种情况：

其中：i表示当前为训练模型的次数；n表示上一次训练模型时的数据源个数；j表示当前训练的数据源；Dij表示增量数据集；s1(Dij)、s2(Dij)、s3(Dij)表示初始化参数的随机森林m1、朴素贝叶斯m2、神经网络m3在增量数据集上训练的模型。

图4 数据收集阶段算法流程Fig.4 Flowchart of data collection stage

图5 模型训练阶段算法流程Fig.5 Flowchart of model training stage

模型存储阶段的算法如图6 所示，可以看到将各个时间段内本地模型的参数使用ECDSA上传至数据块2至n-1中，数据块1中存储的是本轮时间段内初始全局模型，数据块n存储的是本轮更新后的全局模型，以此来保证ti时间段的本地模型以及全局模型的安全，利用区块链的不可逆和不可篡改以及可追溯的特点来保证模型层面上的安全。

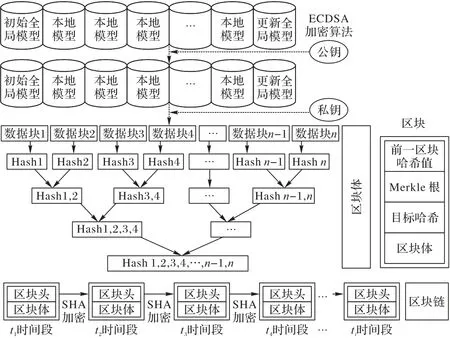
图6 模型存储阶段算法流程Fig.6 Flowchart of model storage stage

综上所述，基于区块链的在线联邦增量学习算法的流程如下：

1）数据收集阶段。

步骤1 由可信第三方使用RSA 加密算法产生的公钥传输至各数据源与客户端；

步骤2 客户端计算数据的hash 值，并将hash 值加密与数据共同传输至数据源；

步骤3 数据源使用私钥解密，并重新计算数据的hash值，将传输前后计算的hash 相等的数据存储至数据源，不相等的删除。

2）模型训练阶段。

步骤1 各数据源使用RSA 加密算法产生的公钥传输至可信第三方；

步骤2 可信第三方将初始化参数的随机森林、朴素贝叶斯、神经网络使用公钥加密并传输至各数据源；

步骤3 各数据源使用初始化参数的3 种模型在历史数据上进行训练，根据3 种初始化参数模型的准确度计算其平均值与方差来衡量模型的性能，将性能最优的作为初始全局模型；

步骤4 从t2时间段起，判断是否有新增加或减少的数据源；

步骤5 若出现新增加的数据源，将初始化参数的随机森林、朴素贝叶斯、神经网络传输至新的数据源，并重新计算并选择性能最优的作为ti时间段的初始全局模型；

步骤6 若减少了数据源，需要根据上一次训练初始全局模型时的准确度重新计算并选择性能最优的作为ti时间段的初始全局模型；

步骤7 若无新增或减少数据源，将ti-1时间段上更新的全局模型作为ti时间段上的初始全局模型；

步骤8 将初始全局模型在ti时间段产生的增量数据上进行训练，获得ti时间段的本地模型；

步骤9 各数据源将ti时间段的本地模型传输至可信第三方；

步骤10 可信第三方使用stacking 集成算法来整合ti时间段的多方本地模型，获得ti时间段上的更新的全局模型。

3）模型存储阶段。

步骤1 将可信第三方在ti时间段上使用ECDSA 算法产生的私钥传输至各数据源，公钥传输至区块i；

步骤2 各数据源使用私钥加密ti时间段的初始全局模型参数、本地模型参数、更新的全局模型参数并传输至区块i；

步骤3 区块i使用公钥解密并将初始全局模型参数、本地模型参数、更新的全局模型参数依次存储至数据块1，2，…，n中。

算法伪代码如下：

2.2 性能分析

2.2.1 算法的复杂度分析

联邦增量学习算法的复杂度为Hash 算法的复杂度、RSA加密算法的复杂度［15］、ECDSA 数字签名算法的复杂度、首轮最优的初始全局模型的复杂度、模型传输的复杂度、首轮模型整合的复杂度、模型更新的复杂度、模型存储的复杂度之和，即时间复杂度为O(((n*log(n)*d*k) +N3+Wk+2+Gk+2)*l)，其中：n表示样本数，d表示特征维度总数，k示决策树数量，N表示加密算法的复杂度，W表示模型传输的复杂度，G表示模型传输的复杂度，l表示轮数。采用联邦学习与stacking 集成算法将必然造成此算法的时间复杂度和空间复杂度均高于传统的数据融合算法。传统数据处理方法的时间复杂度为：O((n*log(n)*d*k) +N3+W+G)，其中，n表示总体样本数，d表示特征维度，k表示决策树数量，N表示加密算法的复杂度，W表示模型传输的复杂度，G表示模型存储的复杂度。因本文算法采用增量上传，联邦增量算法的时间复杂度为：O((n/l*log(n/l)*d*k) +N3+W+G)，通信开销节约的时间复杂度为采用联邦学习与stacking 集成算法在增量数据上进行训练，在保证了所训练模型准确率的情况下，时间复杂度比传统数据处理技术要低。

2.2.2 算法的安全性分析

联邦增量学习算法使用了联邦学习的框架与区块链的性质，从数据层面上，使用RSA 加密算法对每个客户端的数据进行hash 计算，并将hash 值与数据共同传输至各数据源，各数据源重新计算其hash 值，可保证数据在收集阶段的安全性与完整性。从模型层面上可分为两部分：1）从模型传输的角度，使用RSA 加密算法产生的公钥Pij对初始全局模型Hi进行加密并传输至各数据源；各数据源使用私钥pij解密并进行训练，可保证模型传输过程中的安全性。2）从模型存储的角度，由可信第三方使用ECDSA 产生密钥对，使用私钥对ti时间段的初始全局模型Hi、本地模型hi1，hi2，…，hin和更新的全局模型hi进行签名并传输至区块i，区块i使用公钥进行验证并依次存储区块i的数据块中（其中，初始全局模型Hi存储至数据块1，本地模型hi1，hi2，…，hin存储至数据块2，3，…，n-1，更新的全局模型hi存储至数据块n），可保证模型存储过程中的安全性。

2.2.3 算法的时效性分析

联邦增量学习算法采用增量学习的思想：在数据层面上，将各数据源在[ti-1，ti](i=1，2，…，n)时间段内所产生的数据表示为ti-1时间段上训练模型时的数据，从而可保证数据层面的时效性；在模型层面上，将ti-1时间段更新的全局模型hi-1作为ti时间段的初始全局模型hi进行训练，可得ti时间段的本地模型hi1，hi2，…，hin及更新的全局模型hi，从而可保证模型层面的时效性。

综上可以看出，本文提出的在线联邦增量学习算法的准确性比传统的数据融合模型略有下降，但具有很高的时效性与安全性。

3 实验分析

3.1 实验参数设置

该算法由python语言和pycharm集成软件开发实现，实验硬件环境为：Inter Core i5-4200M CPU 2.50 GHz 处理器，内存8 GB；操作系统为Windows 10。在实验数据方面，采用从http：//sofasofa.io/competition.php？id=2 下载的数据集，该数据集有15.6 MB。

3.2 实验数据分析

将数据集随机划分成17 份表示不同数据源（k=1，2，…，17）在不同时间段内所产生的数据，随机对数据集划分100 次能更合理地表示各数据源中的数据。随机划分100次的数据集反映出划分前后数据的变化关系，随机划分数据集可以满足数据源特征相同样本不同的需求，以及可以满足交叉验证模型的合理性。使用RSA 加密算法产生的公钥来加密数据的hash 值，并与数据共同传输至各数据源，各数据源使用私钥解密，且重新计算数据的hash 值，判断数据经过传输的hash 值与传输前的hash 值是否相等，将hash 值相等的数据存储至各数据源内，可保证数据在收集阶段的安全性与完整性。

3.3 实验模型分析

本文实验分为四个部分，第一部分：将随机森林、神经网络、朴素贝叶斯作为初始模型分发至各数据源，在历史数据集上进行训练，根据三种模型训练的结果计算准确度的平均值（mean，即准确率）及方差（variance），选择准确率最高且方差最小的作为初始全局模型。第二部分：将ti时间段的初始全局模型分发至各数据源，并进行训练得ti时间段的本地模型，再使用stacking 集成算法集成本地模型，得ti时间段最有效的更新的全局模型。第三部分：各数据源使用RSA 加密算法产生256 B 的密钥对，将其公钥传输至可信第三方，ti时间段的初始全局模型使用公钥加密并传输至各数据源，各数据源使用私钥解密并进行训练。第四部分：可信的第三方使用ECDSA 数字签名算法产生密钥对，将其私钥传输至各数据源，公钥传输至对应的区块中，各数据源使用私钥对ti时间段的初始全局模型参数、本地模型参数、更新的全局模型参数进行签名并传输至对应的区块，区块使用公钥进行验证并存储相应的数据块中。因随机森林、朴素贝叶斯、神经网络三种模型具有随机性，所以本文将每种初始模型迭代100 次，计算其平均值及方差来衡量初始模型的性能，表1 反映了初始模型在4个数据源的历史数据上的性能。

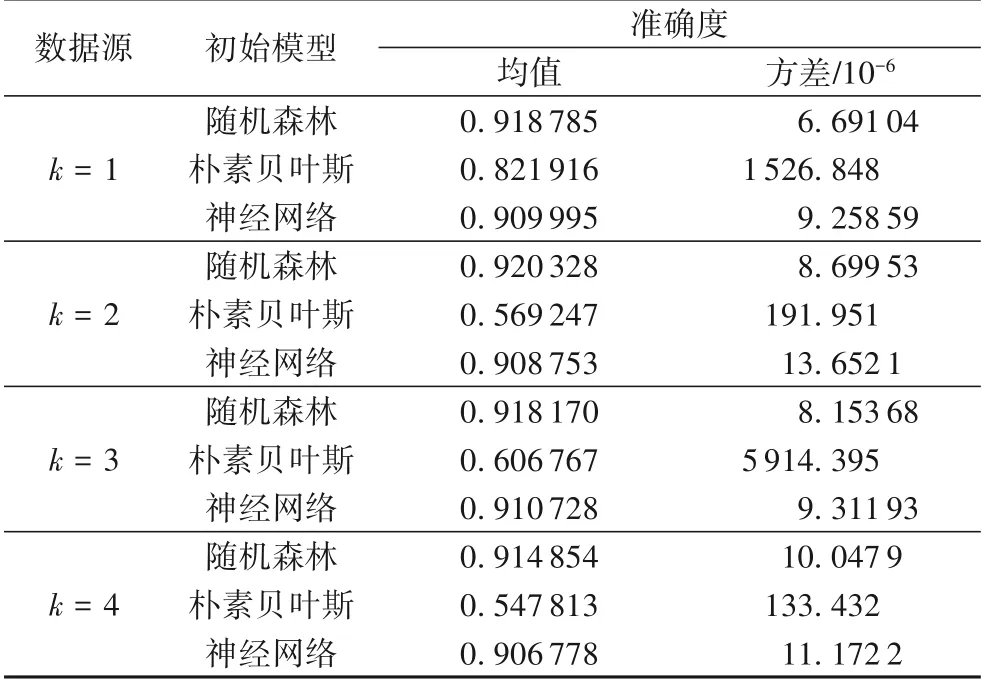
表1 三种初始模型在历史数据上迭代100次的准确度均值与方差Tab.1 Means and variances of 100 iterations of three initial models on historical data

从表1 可以看出，对于历史数据来说，平均值由大到小的顺序是随机森林、神经网络、朴素贝叶斯，而方差由小到大的顺序是随机森林、神经网络、朴素贝叶斯，综合考虑随机森林的性能最优，故本文选择随机森林作为首轮的初始全局模型，且使用stacking 集成算法依次对首轮初始模型在数据源上建立的模型进行集成，得到首轮更新的全局模型的准确度。因随机森林作为初始全局模型具有随机性，且数据为随机划分而成，所以本文将初始模型在随机划分的数据集上迭代10 次的平均值作为数据划分一次模型的准确度，将划分100 次数据的平均值作为首轮模型的准确度。图7 是在历史数据集的4 个数据源上使用随机森林在随机划分一次数据上迭代过程的准确率变化情况。

图7 初始全局模型H0在随机划分一次数据上迭代过程的准确率变化情况Fig.7 Changes in accuracy of a iteration of initial global model H0on once randomly divided data

随机森林在首轮数据的准确度可表示为随机森林在划分100次的数据且在每次划分的数据上迭代10次训练准确度的平均值，可保证每次数据的准确性，同时每次均产生4 个本地模型hin(n=1，2，3，4)，为检验本地模型的性能，采用准确度平均值及方差来衡量。

从表2 可以看出，初始全局模型H0在t1时间段上数据的准确度均值均在91.8%以上，且方差都很小，表明多个本地模型的性能都很好，且本地模型在数据上训练的准确度均值结果几乎相等。

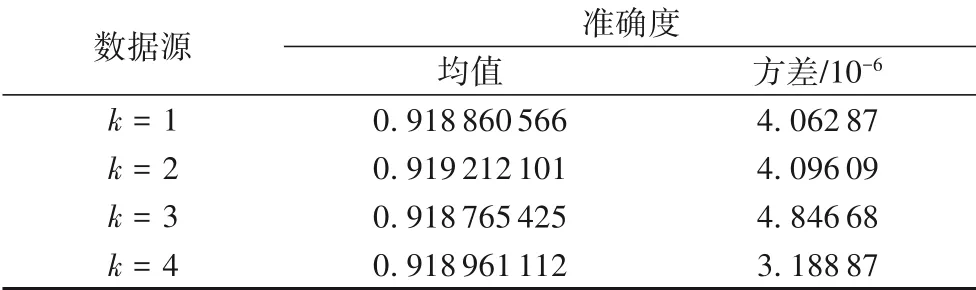
表2 H0在t1时间段的增量数据上迭代100次的准确度均值与方差Tab.2 Means and variances of 100 iterations of H0on incremental data in t1period

将训练的多个本地模型使用stacking集成算法来集成，得到更新后的全局模型h1在t1时间段数据上的准确度保持在91.858%，且方差为4.889 5×10-6，说明更新的全局模型h1有很好的稳定性。

为检验t1时间段更新的全局模型h1在t2时间段上的训练结果，本文算法将会判断在ti时间段上有无新增加或减少的数据源，实验中假设在t2时间段和t1时间段的数据源一致，t3时间段将会减少1 个数据源，t4时间段将会增加1 个数据源，当ti时间段新增加或减少了数据源，那ti时间段的初始全局模型Hi需要重新计算。因t2时间段和t1时间段的数据源一致，所以将t1时间段更新的全局模型h1作为t2时间段的初始全局模型H1，在t2时间段所产生的数据上进行训练。

表3中的数据为t2时间段的初始全局模型H1在每次随机划分的数据上迭代10 次训练的平均值，可保证每次数据的准确性，同时每次均产生4个本地模型hin(n=1，2，3，4)，为检验t2时间段本地模型的性能，仍采用平均值及方差来衡量。

从表3 中可以看到，在t2时间段的初始全局模型H1的准确度均在91.8%以上，且方差都很小，表明初始全局模型H1在t2时间段内所产生的数据上训练的结果均很好，模型很稳定。

将t2时间段训练的多个本地模型使用stacking 集成算法来集成，得到更新后的全局模型h2的准确度保持在91.86%以上，且方差为6.12 × 10-6，说明更新的全局模型h2有很好的稳定性。

表3 H1在t2时间段的增量数据上迭代100次的准确度均值与方差Tab.3 Means and variances of 100 iterations of H1on incremental data in t2period

为充分检验增加或减少数据源对算法的影响，将t3时间段减少1 个数据源（3 个数据源）进行训练，因数据源发生变化，所以需要重新计算t3时间段的初始全局模型H2，同样地使用准确度均值及方差衡量3 种初始模型性能。表4 是三种初始全局模型在t3时间段的增量数据上重新计算的准确度均值与方差的变化情况。从表4 可以看出，随机森林的准确度均值与方差明显优于朴素贝叶斯和神经网络，而神经网络的准确度均值与方差均优于朴素贝叶斯。

表4 三种初始模型在t3时间段的增量数据上迭代100次的准确度均值与方差Tab.4 Means and variances of 100 iterations of three initial models on incremental data in t3period

表5中的数据为t3时间段的初始全局模型H2在每次随机划分的数据上迭代100 次的准确度均值，可保证每次数据的准确性，同时每次均产生4 个本地模型hin(n=1，2，3，4)。从表5可以看出减少数据源可以使初始全局模型H2的准确度有所增加，且方差较小，满足实验性需求。

表5 H2在t3时间段的迭代100次的准确度均值与方差Tab.5 Means and variances of 100 iterations of H2on incremental data in t3period

将t3时间段训练的多个本地模型使用stacking 集成算法集成，得到更新后的全局模型h3的准确度保持在91.931%以上，且方差为5.7×10-6，说明更新的全局模型h3有很好的稳定性。同时可以看到数据源的减少可以使更新的全局模型h3的准确度有所提升，且方差在变小，说明减少数据源可以使模型更加稳定。

为检验增加数据源对联邦增量学习算法的影响，在t3时间段的基础上增加2 个数据源，表6 反映的是初始模型在5 个数据源上训练情况。从表6 可以看出，增加数据源后初始全局模型H3的准确度均有所下降，且方差也都有所增加，但随机森林的准确度依旧很高，模型的稳定性也较好。

表6 三种初始模型在t4时间段的增量数据上迭代100次的准确度均值与方差Tab.6 Means and variances of 100 iterations of three initial models on incremental data in t4period

表7中的数据为t4时间段的初始全局模型H3在每次随机划分的数据上迭代100 次的准确度均值，可保证每次数据的准确性，同时每次均产生4 个本地模型hin(n=1，2，3，4)。从表7 可以看出，增加数据源使初始全局模型H2的准确度有所减小，且新增加的数据源所对应的方差比原有数据源的方差要大，但还是能满足实验需求。

将t4时间段训练的多个本地模型使用stacking 集成算法来集成，得到更新后的全局模型h4的准确度保持在91.588%以上，且方差为9.315× 10-6，说明更新的全局模型h4有很好的稳定性。同时可得到在增加数据源后，在t4时间段的数据上，全局模型h4的准确度达到91.59%，且方差很小。

表7 H3在t4时间段的增量数据上迭代100次的准确度均值与方差Tab.7 Means and variances of 100 iterations of H3on incremental data in t4period

传统的多源数据源处理技术将多方数据整合后再进行训练，所训练的模型准确率为92.521%，方差为0.934 × 10-6（为保证数据的准确度与真实性，该数据为随机森林在整合的数据上迭代100次的准确度均值与方差）。

为保证每次初始全局模型Hi能够安全传输至各数据源，需使用256 B的公钥加密模型进行传输。

图8反映出可信第三方与各数据源使用RSA 加密算法在不同的时间段内产生的公钥与私钥的变化情况，可信第三方使用不同的公钥来加密不同时间段的初始全局模型，进而提升不同时间段内初始全局模型传输的安全性；同时，各数据源使用不同的公钥来加密本地模型并传输至可信第三方，可以提升不同时间段内本地模型传输的安全性。

图8 RSA加密算法的公钥、私钥变化图Fig.8 Public and private key changes of RSA encryption algorithm

为保证模型在传输过程的安全性以及防止模型被篡改与攻击的风险，本文由可信的第三方使用ECDSA 数字签名算法产生密钥长度为570 的密钥对与RSA 加密算法产生的256 B的密钥对，图8 反映出RSA 加密算法产生的密钥对的变化情况，各数据源将RSA 加密算法产生的公钥传输至可信第三方，私钥保留在各数据源中。

各数据源使用图9（b）中的私钥对每个时间段的初始全局模型、本地模型、更新的全局模型使用由第三方提供的私钥进行签名，并传输至对应区块的数据块中。区块链中对应区块的数据块使用图9（a）中的公钥进行验证，验证过程能够验证模型参数是否完整地传输至数据块中，同时也能降低模型在传输过程中被篡改及攻击的风险。

图9 ECDSA的公钥、私钥变化图Fig.9 Public and private key changes of ECDSA

对于模型存储阶段，RayBaaS 平台能够快捷、高效地构建基于区块链的服务和应用，硬件设备采用Inter Core i5-4200M CPU 2.50 GHz 处理器进行实验，区块链底层基于CentOS 7.6操作系统进行部署，存储的数据包括ti时间内的初始全局模型参数、本地模型参数、更新的全局模型参数，将t1时间段内的初始全局模型参数存储至区块1的数据块1中，本地模型参数存储至区块1的数据块2、3、4、5中，更新的全局模型参数存储至区块1的数据块6中；将t2时间段内的初始全局模型参数存储至区块2的数据块1中，本地模型参数存储至区块2的数据块2、3、4、5中，更新的全局模型参数存储至区块2的数据块6 中；t3时间段内的初始全局模型参数存储至区块3 的数据块1 中，本地模型参数存储至区块3 的数据块2、3、4 中，更新的全局模型参数存储至区块3的数据块5中；t4时间段内的初始全局模型参数存储至区块4的数据块1中，本地模型参数存储至区块4的数据块2、3、4、5、6中，更新的全局模型参数存储至区块4的数据块7中。

3.4 实验小结

在线联邦增量学习算法将随机森林、神经网络、朴素贝叶斯分发至历史数据上进行训练并迭代100 次，计算其准确度均值及方差作为衡量初始全局模型的标准，其中随机森林在历史数据上的准确度为91.4%，且方差均小于1.2 × 10-5，所以将随机森林作为首轮初始全局模型并分发至数据源进行训练，且使用stacking 集成算法集成多个本地模型，获得更新的全局模型h1在t1时间段内所产生的数据的准确度为91.858%。因t2时间段并无新增数据源，则将更新的全局模型h1作为t2时间段的初始全局模型分发至数据源并进行训练，并使用stacking 算法来集成多个本地模型，获得的全局模型h2的准确率为91.86%，表明更新的全局模型h2具有很强的泛化性。为研究增加与减少数据源对初始全局模型的影响，在t3、t4时间段分别减少1 个数据源和增加1 个数据源，重新计算其平均值及方差，得到在t3时间段内所产生的数据上随机森林的准确度最高，且均在91.8%以上，使用stacking 集成后的准确度为91.9%；在t4时间段内所产生的数据上随机森林的准确度最高为91.5%，使用stacking集成后的准确度为91.58%，说明增加与减少数据源会对初始全局模型产生影响。使用传统的数据处理技术将多方数据整合后再进行训练，获得的模型的准确率为92.521%，与之相比，本文算法的准确度仅下降约1%，但数据及模型在训练过程中的安全性得到很大提升。

4 结语

本文提出了一种面向区块链的在线联邦增量学习算法，采用数字签名的方式保证数据在收集阶段的安全性与完整性；使用stacking 集成算法来整合多方本地模型，虽然模型的准确率略有下降，但模型的安全性得到提升，同时模型在增量数据上进行训练，使模型具有时效性；将每个时间段的初始全局模型参数、本地模型参数、更新的全局模型上传至对应数据块中并快速同步，使数据的传输成本降低，同时模型参数的安全性得到了保障。接下来的工作中，我们会尝试将本文算法应用到其他隐私保护技术中，在保证模型准确率的基础上，进一步提升数据与模型的安全性。