一种基于改进PCA和BP神经网络的人脸识别算法

岳 也，王川龙

(太原师范学院 数学系，山西 晋中 030619))

0 引言

人脸识别在身份识别、经济领域等相关科学领域中是一个热门的话题[1，2].PCA方法是由Turk和Pentlad提出来的[3，4]，是以K-L(Karhunen-Loeve 的缩写)正交变化为基础，将数据从高维空间投影到低维空间，从而达到降维数据维数的目的[5].

李荣建等[6]提出改进PCA人脸识别算法，增大每幅图片的亮度和对比度，有效地减少光照对人脸识别的影响.徐肖亮等[7]利用矩阵范数对协方差矩阵进行约简，一定程度上降低了计算量.李康顺[8]等结合一种新的权值调整方法改进BP算法并进行图像分类识别.柳长源等[9]在进行人脸图像识别之前先利用小波分解和PCA 算法进行图像消噪预处理，传统的K-L 变换在图像的特征降维过程中存在运算量较大的问题.此外，更多的学者则是针对人脸识别过程中的图像数据降维及识别算法做了大量的研究，徐竟泽[10]等利用PCA消除图像特征间的相关性，用基于SVM 的LDA算法进行数据降维的人脸识别方法.廖周宇[11]等提出一种基于粒子群优化的支持向量机人脸识别方法，以上几种方法在人脸识别率方面都有不错的效果.

本文针对传统PCA算法在对协方差矩阵进行特征提取时计算量大且易受光照等因素影响的问题，提出一种改进的快速PCA 算法，选用ORL人脸图像数据库，利用BP神经网络进行训练与测试，并验证了该算法的有效性.

1 相关算法

本章主要介绍了PCA算法及BP神经网络算法.

1.1 PCA算法相关内容

主成分分析 (Principal Component Analysis，PCA)是一种常用于处理数据的方法[12].由于传统的 PCA降维对样本的协方差矩阵进行特征值和特征向量的求解计算量较大，需要耗费较多的时间，为了提高人脸识别率，本文提出一种改进的快速 PCA 算法.

1.1.1 PCA人脸图像特征提取

人脸识别一般包括四个步骤：人脸图像采集、人脸图像预处理、人脸图像特征提取、特征匹配与识别[13].首先采集人脸图像进行预处理，形成一个人脸数据库，然后将采集到的样本分为训练集和测试集，最后用不同的方法学习训练集样本，进行分类测试识别.因为人脸图像在采集、传输、处理过程中有光照阴影，噪声污染，设备质量问题等因素干扰，会从一定程度影响识别效果.

1.1.2 PCA算法要点

1.1.2.1 协方差矩阵

特征Xi与特征Xj的协方差(Covariance)：

(1)

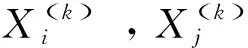
1.1.2.2 特征向量与特征值

对于矩阵A，若满足Aζ=λζ，则称ζ是矩阵A的特征向量，而λ则是矩阵A的特征值.

算法1(传统PCA算法)

第0步：给定M张人脸组成原始图片集X=[x1,x2,…,xM],低维空间维数d；

第2步：计算样本的协方差矩阵φ=XXT；

第3步：通过SVD分解求出该协方差矩阵φ的特征值λ=(λ1,λ2,…,λM)和特征向量V=(v1,v2,…,vM)；

第4步：对求出的特征值用降序方式排列φ=λ·V；

第5步：计算协方差矩阵特征值的累计贡献率,取前r个较大的特征值所对应的特征向量V=(v1,v2,…,vr)作为降维后的子空间；

第6步：输出降维后的数据集V.

1.1.3 PCA降维

A为图像样本矩阵，Zn×m为A中的每个样本减去样本均值后得到的矩阵，其中n为样本数量，m为样本维数.假设n维列向量ν是矩阵(ZZT)的特征向量，则有:

(ZZT)ν=λν

(2)

将式(2)两边同时乘以ZT得到:

(ZTZ)ZTν=λZTν.

(3)

图1 三层BP神经网络

从以上的计算过程可以看出，在进行人脸图像的特征降维时，可以通过计算低维度矩阵(ZZT)的特征向量ν，对其左乘ZT，得到协方差矩阵的特征向量.

1.2 BP神经网络算法

BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈网络，其识别率比传统算法及人工特征提取方法的识别率高[14].

1.2.1 BP神经网络架构及其思想

BP的拓扑结构如图1：输入层(input)的节点数是数据样本经矩阵分割以后所得的特征向量的维数，输出层(output)的节点数为人脸数据库的类别数，隐含层(hide layer)的节点数通常由经验公式确定大致范围，再通过实验选取具体合适的数值作为参数[14].

2 基于BP神经网络的改进人脸识别算法

为了验证本文提出的基于快速PCA人脸识别改进算法的效果，在Matlab2013a环境下实现编程，操作系统为Windows7.

实验的人脸图像来源于ORL人脸图像数据库，该数据库共400幅灰度图像，每个人10张图像，由各种角度、表情拍摄而成.其中部分图像如图2所示.

图2 ORL部分人脸图像

2.1 基于BP神经网络的改进PCA算法流程

基于BP神经网络的改进PCA算法的人脸识别方法的具体步骤为:

1)将原始ORL人脸图像转化为灰度矩阵，再对灰度矩阵进行矩阵分割，本文实验分割成16，24，80个小矩阵，对每一个小矩阵中心化代替原矩阵，求出每一个矩阵的协方差矩阵，再对每一个小矩阵进行特征值提取，选择每一个矩阵最大的特征值所对应的特征向量组成图片的特征矩阵.

2)将数据集的均值归零，即只取数据的偏差部分，对处理得到的特征矩阵进行划分，将其划分为训练集train_data和测试集test_data，用以训练和测试.

3)从每个人的文件夹中选出构造训练集的图片数目，该值必须大于0，小于10.本文选择每人5张图片作为训练，剩余5张作为测试，建立测试目标集，并对训练集和测试集进行归一化处理.

4)构建BP神经网络.输入BP神经网络所需的隐含层神经元个数，输入层与隐含层之间的传递函数tansig，隐含层与输出层之间的传递函数purelin，BP训练函数trainrp，输入训练目标，训练次数以及学习速率.

5)训练BP神经网络.得到训练后的神经网络以及训练过程记录.

6)用训练好的BP神经网络进行识别，得到分类正确的测试集数目和分类正确的训练集数目以及总识别率.

3 实验结果

为了进一步验证人脸识别效果，将本文所提出的改进人脸识别算法记为GPCA算法，并将改进的地方应用在传统的PCA算法上进行比较.

3.1 PCA特征提取改进算法

改进PCA特征提取算法(GPCA算法)：

算法2(GPCA算法)

第0步：M张人脸组成原始图片集X=[x1,x2,…,xM],特征维数数目(16,24,80)；

第1步：对图片数据集进行预处理转化为灰度矩阵，将灰度矩阵划分成(16,24,80)个小矩阵Z=[x1,x2,…,xM]；

第3步：计算每一个小矩阵的协方差矩阵φ=XXT；

第4步：对每一个协方差矩阵做特征值分解；

第5步：取每一个小矩阵最大的特征值λ以及所对应的特征向量v；

第7步：输出降维后的特征矩阵V.

这样提取出的特征值更加具有代表性，经实验验证，本文算法正确识别的训练集数目和测试集数目比传统提取特征值的PCA 算法识别出的正确数目要多，识别率也比传统PCA算法的识别率高.

3.2 ORL数据库实验结果

本文实验从ORL人脸数据库中每个人选出5张用于训练，剩余5 张用于测试.用训练好的BP神经网络进行识别，得到分类正确的测试集数目和分类正确的训练集数目.表1、表2、 表3即为两种算法基于输入层不同的情况，在ORL数据集上的训练正确数目和测试正确数目的结果对比.

表1 输入层为16的ORL人脸图像实验结果

表2 输入层为48的ORL人脸图像实验结果

表3 输入层为80的ORL人脸图像实验结果

3.3 BP神经网络的实验结果

经过大量的实验选择BP神经网络的参数，如图3所示，网络训练方法为按比例缩小的共轭梯度法.图3、图4、图5、图6 是ORL人脸数据库在BP网络训练过程.

图3 BP网络的参数训练图4 BP网络性能图

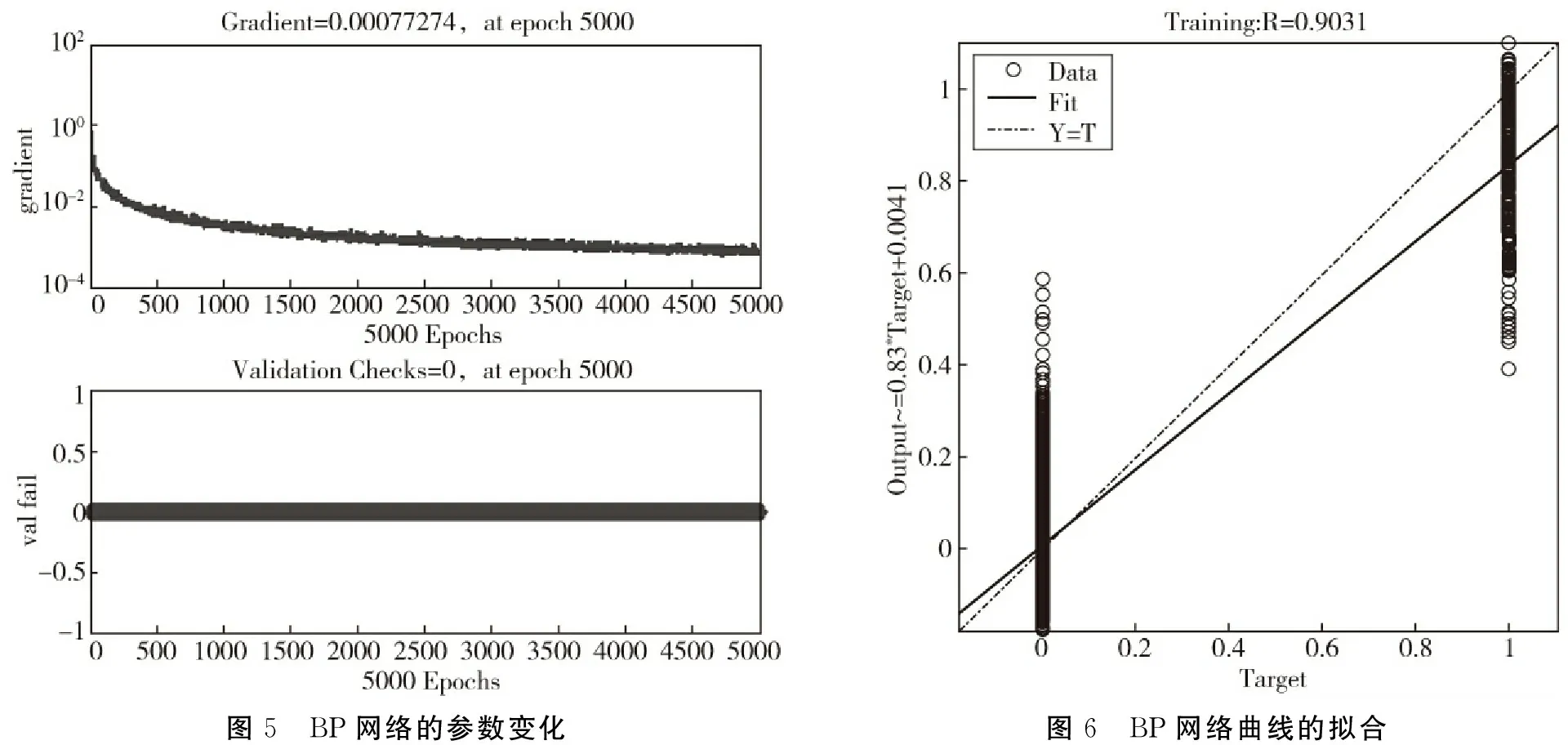
图5 BP网络的参数变化图6 BP网络曲线的拟合

3.4 改进GPCA算法的人脸图像实验结果

表4、表5、表6为两种算法基于输入层和隐层不同的情况，BP神经网络的识别结果对比.

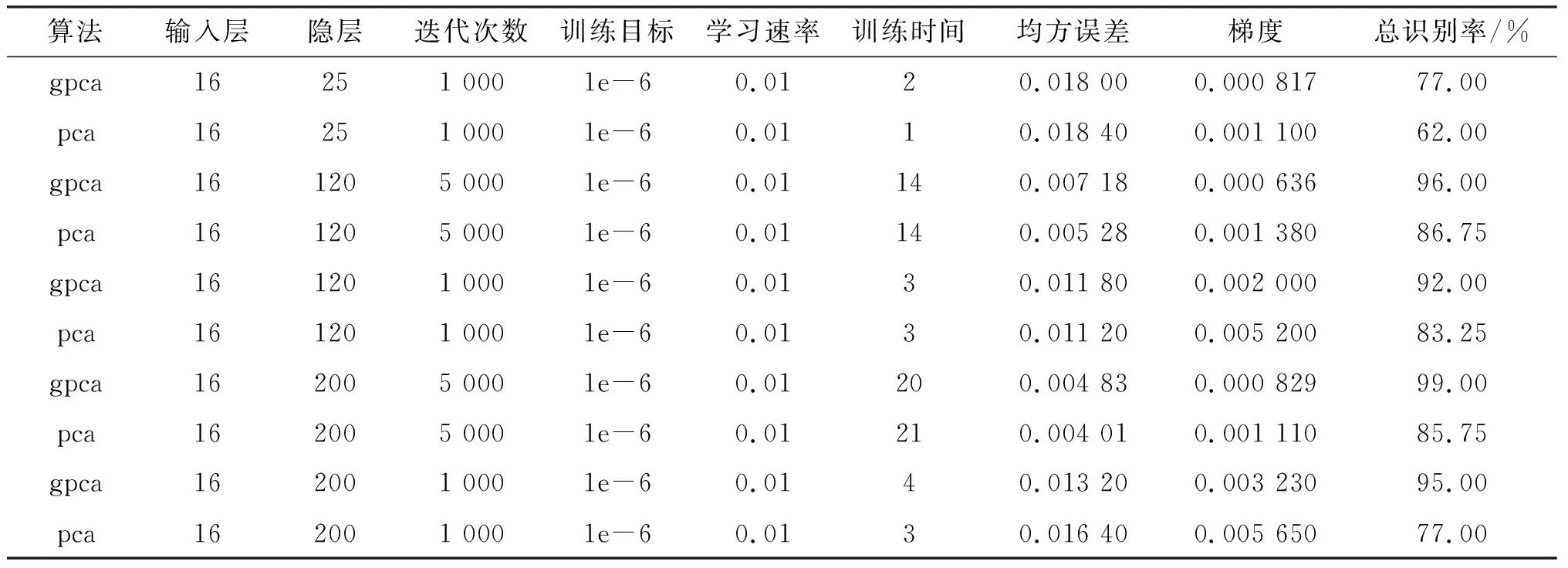
表4 输入层为16的人脸图像实验结果

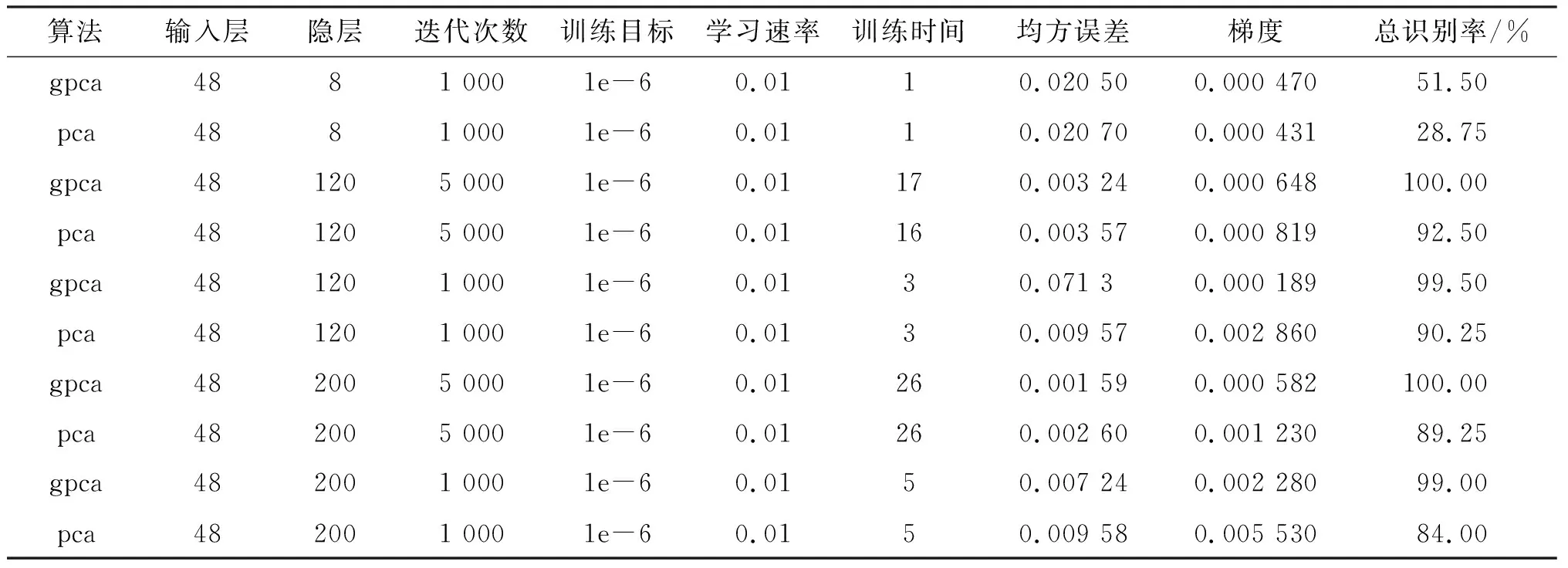
表5 输入层为48的人脸图像实验结果

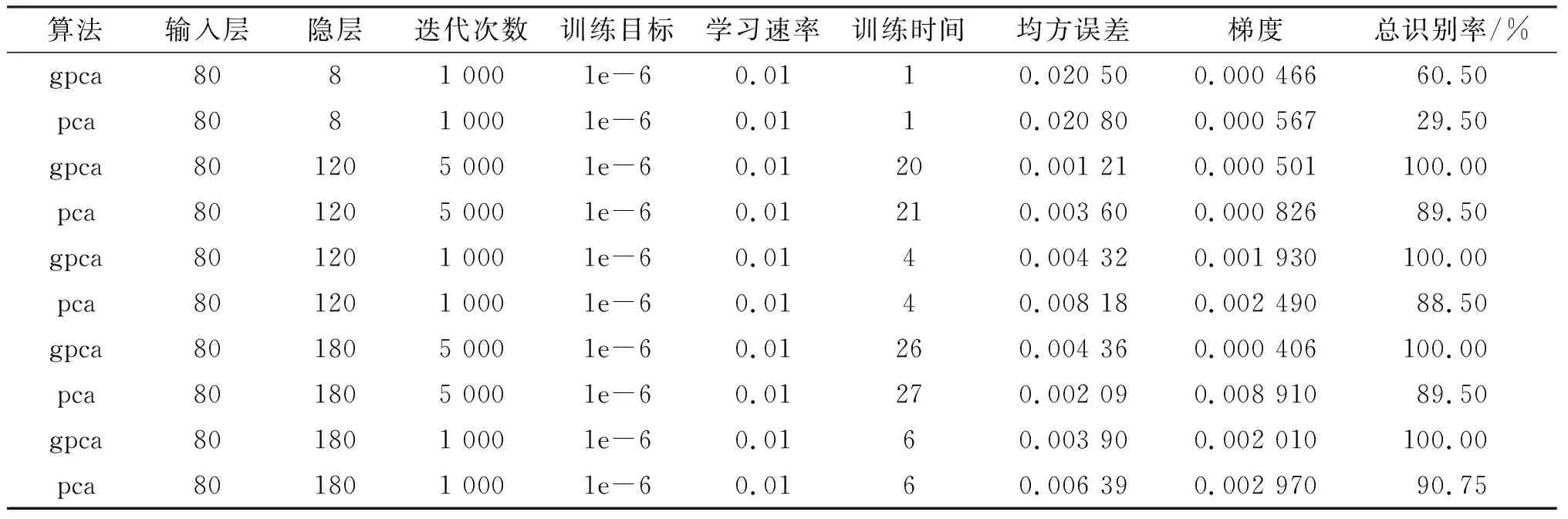
表6 输入层为80的人脸图像实验结果

4 小结

本文所选取的人脸图像数据集为ORL数据库，共400张图片，前200张用作训练集，后200张用作测试集.从表1、表2、表3可以看出，本文算法相比于算法1在正确识别总训练图片数和总测试图片数上有所改进，正确率变高.

从图6可以看出BP神经网络训练未出现过拟合或者不拟合现象.

从表4、表5、表6可以看出，当隐含层数很小时，传统PCA算法的识别率非常低，而GPCA算法的识别率明显提高；当隐层，训练目标和学习速率均相同时，不论是传统PCA算法还是GPCA算法，迭代次数选择5 000次均比1 000 次的总识别率要高；选择划分为16 个小矩阵时，即输入层为16时，当隐层数大于等于120时，传统PCA算法的识别率均不超过90%,而GPCA 算法的识别率均超过了90%;当划分的小矩阵为48个时，传统PCA算法在隐层数为120，迭代次数为5 000，训练目标为1e-6，学习速率为0.01 时，总识别率达到最高，为92.5%，而GPCA算法在同样的参数变量下，总识别率达到了100%.

本文实验还存在一些不足之处：

1)本文在计算特征值与特征向量的过程中，分割矩阵维数有限，不是任意维数均可.

2)分类识别方法只选用了BP神经网络进行，今后还需要再进行研究，看看是否可以在分类识别算法上进行改进，在实现识别率高的情况下，运行时间也缩短.