基于FP_Growth算法的关联规则挖掘研究及应用

马瑞敏，吴海霞

(长治学院 计算机系，山西 长治 046011)

0 引言

随着计算机技术、移动互联网与物联网的高速发展，可供人们采集利用的数据越来越多，呈现爆炸式增长.大量的数据背后隐藏着许多重要的信息，如何对其进行更高层次的分析，并转换成有用的信息和知识，成为数据挖掘技术研究的主要内容.关联规则挖掘是数据挖掘的一个重要分支，其概念最早由美国科学家R.Agrawal等人于1993年提出，最初用于挖掘顾客交易数据库中用户购买的商品之间内在的隐含关系及关联规则，从而为决策者提供决策支持.现在关联规则挖掘不但在商业分析中得到了广泛的应用，在通信、金融、交通、健康医疗和Web用户行为分析等领域也得到了广泛应用.

1 关联规则及其抽象描述

关联规则挖掘主要用于发现存在于数据库中的项或属性间的关联关系.设I={I1,I2,…,Im}是项的集合，其中m表示项的数目.对于项集A，若A中含有的项数为k(k≤m)，则称A为k-项集[1].D为数据库事务的集合，用|D|表示事务集中事务的个数.对于每个事务T有T={t1,t2,…,tm}，ti∈I，T≠∅.关联规则是形如A⟹B的蕴涵式，其中A⊂I，B⊂I，A≠∅，B≠∅，并且A∩B=∅.表示事务T在含有项集A的条件下，同时含有B的概率[2].用户关心的关联规则，可以用两个标准来衡量：支持度和可信度.

1.1 支持度

支持度的意义在于度量项集在整个事务集中的重要性.我们在发现规则时，总希望找到高概率出现的项集.单一项集的支持度表示该项集在事务集中出现的概率.即，

support(A)=P(A)=count(A)/|D|.

规则A⟹B的支持度，表示项集{A,B}在事务集中同时出现的概率.即，

support(A⟹B)=P(A∪B)=count(A∪B)/|D|.

最小支持度是项集的最小支持阈值，记为min_sup，代表了用户关心的关联规则的最低重要性[3].

1.2 置信度

置信度通常用来衡量规则的可信程度，表示在关联规则的先决条件A发生的条件下，关联结果B发生的概率[4].计算公式如下：

confidence(A⟹B)=P(B|A)=P(AB)/P(A)=
support(A∪B)/support(A)=count(A∪B)/count(A).

最小置信度是置信度的最低阈值，记为min_conf，代表关联规则的最低可信度.

1.3 频繁项集和强关联规则

支持度不小于min_sup的项集称为频繁项集.如果规则A⟹B满足support(A⟹B)〉=min_sup且confidence(A⟹B)〉=min_conf,则称A⟹B为强关联规则.min_sup和min_conf通常由用户根据先验知识来设定.

2 关联规则挖掘的相关算法及分析

关联规则挖掘的目标就是要找出所有的强关联规则.挖掘过程主要分为两步：

步骤1：找到所有不小于最小支持度阈值的规则，即所有频繁项集；

步骤2：对频繁项集进行过滤，滤掉小于最小置信度的项集，找出强关联规则.

步骤2只需根据步骤1找出的频繁项集使用简单的计算就能得出，因此关联规则挖掘算法的核心在于频繁项集的挖掘.最简单的算法是穷举所有的项集组合作为候选集，然后分别检验支持度是否满足预先设定的阈值.这种算法虽简单，但计算效率却很低.随着特征维度的增大，候选集数量会呈指数级增加；且对于每一个候选项集，都需要扫描数据集计算其支持度，当数据量很大时，需要的计算量也很大[5].显然这种暴力算法不是最好的选择，因此人们致力于寻找更为高效的算法，其中FP_Growth算法是较为经典的算法.

2.1 FP_Growth算法

FP_Growth算法是韩家炜等人于2000年提出的一个关联规则挖掘算法.它设计了一种称为频繁模式树(FP-tree)的数据结构，将原始数据集进行压缩存储.树的根结点为“null”，其余节点代表一个特征项及其支持度信息，每一个项集对应树上的一条路径.为了更加快速地挖掘频繁项集，FP-tree还包含一个两列的频繁项表.第一列是特征项名称，按照特征项支持度降序排序.第二列存储一个链表，将FP-tree树中相同特征项的节点连接起来.FP_Growth算法主要分为构建FP-tree和基于FP-tree递归的挖掘频繁项集两个步骤[6].

FP-tree的构建方法如表1所示.FP-tree构建完成后，便可基于它来挖掘频繁项集.分别以频繁项表中的项作为后缀，构造它的条件模式基，条件模式基是FP-tree中与该后缀一起出现的前缀路径的集合.通过条件模式基构造该项的条件FP-tree,并递归地在该树上进行挖掘.模式增长通过后缀模式与条件FP-tree产生的频繁项目连接实现[7].具体流程如图1所示.

表1 FP-tree构建算法

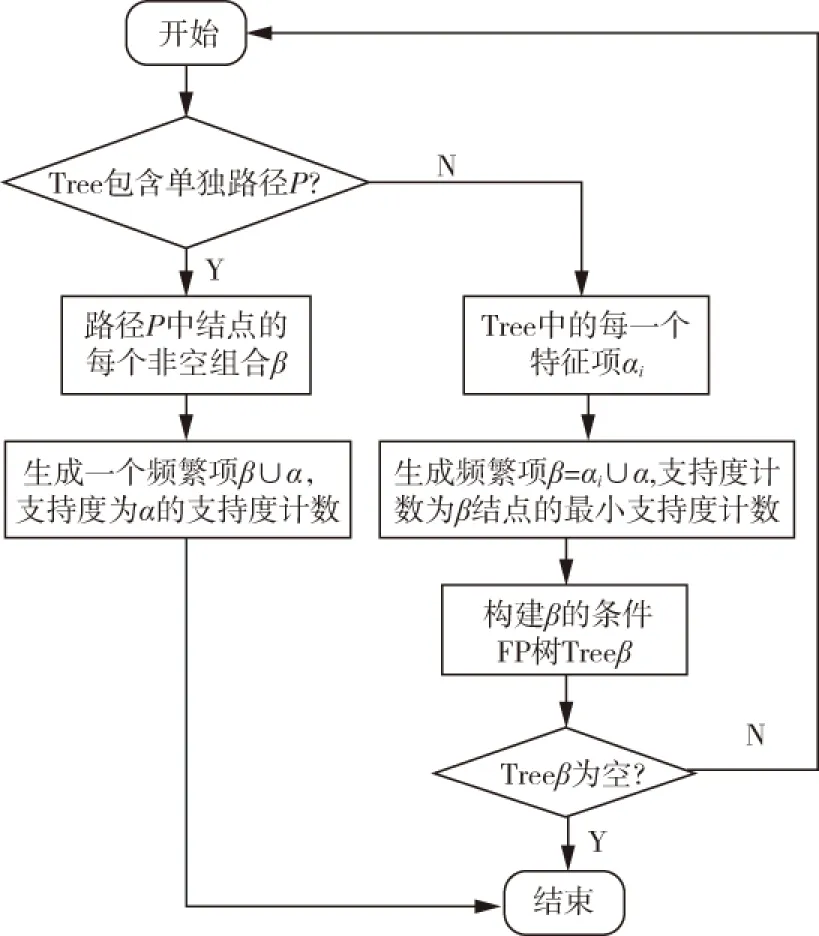
图1 基于FP-tree挖掘频繁项集流程图

FP_Growth算法通过两次遍历原始数据集，将数据以FP-tree的形式进行压缩存储.后续频繁项集的挖掘直接利用FP-tree，避免生成无用的候选项集，大大提高了效率.但该算法生成的是频繁项集，而不是关联规则.如要进一步生成关联规则，需根据频繁项集生成候选关联规则，然后通过最小置信度对关联规则进一步过滤，得到强关联规则.

表2 商品交易数据集

2.2 FP_Growth算法实例演示

下面以商品交易数据集为例演示算法实现过程.该数据集中有6位顾客的购买记录,如表2所示，设定最小支持度为3.

步骤1：扫描数据集，构建FP-tree.

a.第一次扫描数据集，得到频繁1项集的集合，并按支持度降序排列.结果集记为：L1，即L1={{z:5}，{x:4}，{y:3}，{r:3}，{s:3}，{t:3}}.

b.创建FP-tree，构建根结点，标记为“null”,创建频繁项表，将链表设置为空.

c.第二次扫描数据集，对每个事务中的项都按L1中的次序排序并滤掉不频繁的项.

加入第一个事务后FP-tree如图2所示.依次加入其他事务后完整的FP-tree如图3所示.

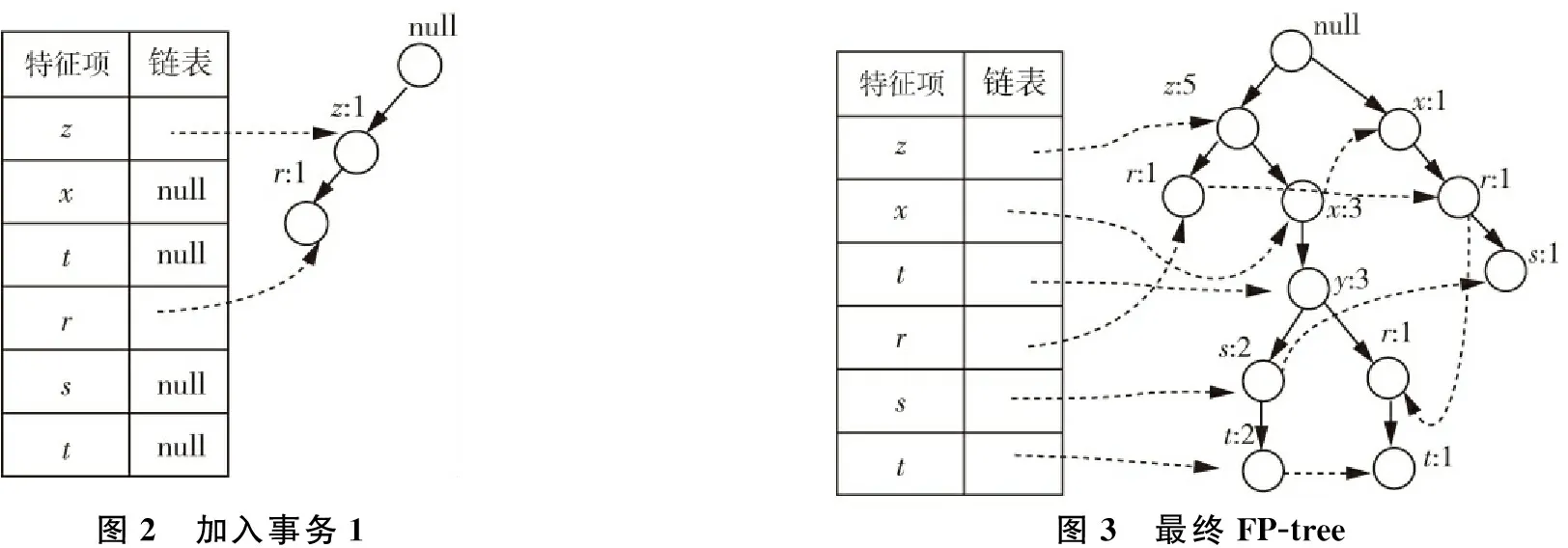
图2 加入事务1图3 最终FP-tree

步骤2：挖掘频繁项集.

首先以t为后缀，找出它的条件模式基：{{z，x，y，s:2}，{z，x，y，r:1}}.使用这些条件模式基构造t的条件FP- tree，它只包含单个路径〈z:3，x:3，y:3〉，不包含s，r，因为这两个项的支持度计数小于3.因此产生了以特征项t为后缀的所有频繁模式.同理依次可以产生s，r，y，x，z的频繁项集如表3所示.

表3 通过条件模式基挖掘FP- tree

3 FP_Growth算法在问卷调查中的应用

用于关联规则挖掘的数据集来自于网站https://www.kaggle.com，主要针对大学生开展的一项问卷调查，收集年轻人爱好和生活习惯等方面的信息.调查问卷共涉及1 010人关于150项问题的调查，例如兴趣爱好、消费习惯、卫生习惯、以及性别、身高、体重等个人基本信息.

3.1 数据预处理

FP_Growth算法只能处理布尔类型的数据，因此在进行数据分析之前，首先要进行预处理.

1.数据删除.本案例收集到的问卷中少量存在未填写的项目，删除将不会影响数据分析的结果，因此对存在缺失值的样本进行了删除.

2.数据转换.数据集中既有数值型数据又有字符型数据,为了转换成适合挖掘的形式，需要对属性取值进行处理.本案例中绝大多数特征的取值范围根据学生的喜爱度分为五个等级，对于这类数据直接进行二值化处理，设定阈值为3，当特征值大于3时赋值为1否则为0.对于年龄、身高、体重等连续型特征变量，先进行变量离散化，然后进行特征编码.对于字符型特征值，也使用特征编码的方式进行了处理.最终生成的新数据集属性数量由150增加为175个，取值均为0或者1.

3.2 数据分析

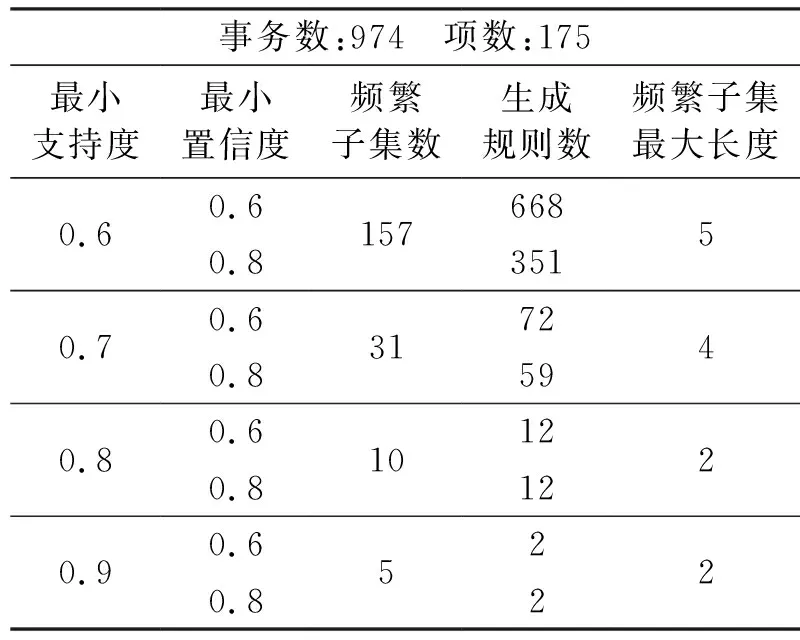
表4 不同参数下的运行结果

通过FP_Growth算法挖掘频繁项集，当设置不同支持度和置信度时，挖掘到的频繁子集个数和生成关联规则数目如表4所示.通过运行结果可看出，当最小支持度为0.8时，产生的频繁子集个数为10，生成关联规则的置信度都很高，均在0.9之上，因此最小置信度设置为0.6或0.8生成的规则数都是12条.置信度排在前三位的关联规则分别为：

Confidence(看电影⟹听音乐)=0.963

Confidence(与朋友玩⟹听音乐)=0.96

Confidence(与朋友玩⟹看电影)=0.932

经过分析，我们可以了解到学生普遍的生活状态和兴趣爱好.比如和朋友玩耍时选择一起看电影、听音乐频度较高；读书、上网、户外运动、社团活动等这些大学生活的重要组成部分伴随出现的频度也较高.此外还发现遵守约定、守时、爱护公物等一些好的生活习惯也是学生比较重视的.

4 结束语

本文对数据挖掘中的关联规则算法进行了研究，重点分析了利用FP_Growth算法构建FP-tree和递归挖掘频繁项集的过程，并将该算法应用于学生兴趣爱好的问卷调查结果分析中.通过发现隐藏在数据中的关联规则，可以帮助老师更深入准确地了解学生的生活习惯，个性特点和兴趣爱好，以便提供更好的生活服务和有针对性地开展丰富多彩的文化活动，营造积极向上朝气蓬勃的校园环境.