钢制薄壁车轮弯曲疲劳模拟精度探讨
2021-03-05覃海艺
覃海艺,马 宁
(上海交通大学塑性成形技术与装备研究院,上海200030)
1 引言
车轮作为汽车一个重要安全部件,在使用之前需通过多种安全性能测试试验,其中,弯曲疲劳试验是用于检测车轮安全性能的主要测试标准之一[1-2]。随着有限元技术与计算机计算能力的发展,人们开始用有限元分析技术替代试验,大大缩短和节约产品设计周期和成本。就车轮弯曲疲劳试验而言,已有多位学者采用有限元技术来模拟实际产品试验过程[3-5],但纵观这些论文的研究方法和过程,发现人们对有限元分析过程的关键步骤介绍甚少,甚至有些学者对影响计算精度的重要环节认识不足,对影响分析结果的重要参数把控不严,分析得到的结果准确性值得再考证。
将以某幅板式钢制薄壁车轮为研究对象,详细描述用有限元分析方法来模拟车轮弯曲疲劳寿命的方法与步骤,着重讲述影响计算精度的因素和注意事项,为此类车轮的弯曲疲劳试验提供一套完整可靠的有限元分析方法指南。
2 车轮弯曲疲劳试验方法
参照GB/T 5909-2014 商用车辆车轮性能要求和试验方法,车轮弯曲疲劳试验方法,如图1 所示。
将轮辋内侧圆面固定于试验台上,在轮辐安装点用螺栓连接一根长度固定的刚性力臂,在力臂自由端施加一个外力F,力的大小依法规要求而定,力与力臂的轴线垂直并绕轴线转动,力每旋转一周,记车轮疲劳寿命1 次,直至车轮发生破坏,力所转动的圈数,即为车轮的疲劳寿命次数。
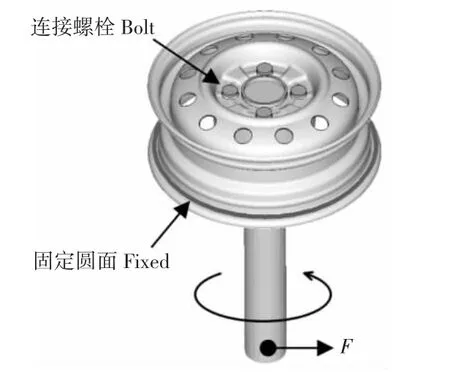
图1 车轮弯曲疲劳试验方法Fig.1 Wheels Bending Fatigue Test
3 有限元分析步骤
3.1 有限元网格模型建立
本算例的分析对象为一幅板式钢制车轮,车轮最小直径为340mm,轮辐厚度3.4mm,轮辋厚度2.4mm,是典型的薄壁构件。参照文献[6]的研究成果,认为网格类型、单元尺寸、厚度方向的单元层数、单元积分形式等参数都是影响薄壁车轮计算精度的主要因素之一。当采用全积分六面体单元,单元长高比接近1:1 时,厚度方向只需两层单元就可以得到较好的应力计算精度。单元长高比越大,全积分单元剪切锁死问题越明显,计算精度越差。虽然减缩积分单元可以得到较准确的位移计算结果,但由于减缩积分单元积分点个数较少,其应力分析结果误差比较大,厚度方向单元个数需5 层以上才能得到较合理的应力分析结果。但厚度方向单元层数过多会导致单元过于细长,对应力计算精度有影响。而要同时保证厚度方向单元个数足够多及单元尺寸不细长,就只能加密结构表面单元数量,这样又会导致单元总数过多,计算时间过长,甚至电脑无法计算。减缩积分单元还有个最大的缺陷就是对临近塑性变形区域的位移和应力分析精度都比较差,因此认为减缩积分单元不适合薄壁弯曲结构件的应力分析。本算例的钢制车轮选用全积分六面体单元较为理想,但必须严格控制单元长高比不能过大。
综合以上讨论,分析采用六面体全积分单元对车轮进行有限元网格划分。考虑到应力是后期疲劳分析的主要输入参数,经权衡计算时间和应力计算精度,除了螺栓孔附近,对车轮其它位置的厚度方向只设2 层单元,同时控制轮辐平均单元长高比在1.2 以内,轮辋平均单元长高比在1.5 以内,整个车轮共8.7 万个单元,13.2 万个节点,如图2 所示。
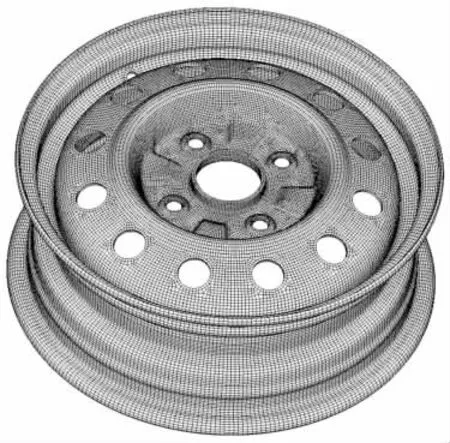
图2 有限元网格模型Fig.2 Finite Element Model
3.2 材料参数确定
通过拉伸试验得到的是材料“工程应力-应变”曲线,它反映的是外力与结构初始截面积的比值,是一种名义应力。而有限元分析是变形逐步积累后的应力结果,它反映的是外力与结构变形时刻实际截面积的比值,是结构真实应力的表现,因此在进行有限元分析之前应把材料“工程应力-应变”曲线转化为“真应力-应变”曲线,转化公式如下[7]:

式中:σ 和ε—工程断裂应力和应变;σT和εT—真实断裂应力和应变。
3.3 边界条件施加
边界条件包括外力、接触关系和固定约束等,根据试验要求,如图1 所示。对轮辋内侧圆面施加固定约束,焊缝位置设为共节点,有接触关系的区域设置为接触边界条件,如轮辐与轮辋、螺栓与车轮、车轮与刚性力臂等之间都需设置接触关系。由于力F的大小不变,力的方向近似在平面内呈圆周旋转变化,为了在有限元分析中完成这种变方向的外力加载,可在旋转平面(xy 平面)内构造两个随旋转角度θ 变化的力函数f(x)和f(y):

其中,0≤θ≤2π。
3.4 螺栓预紧力施加
螺栓预紧力大小对车轮应力分布,尤其是对螺栓孔周围的应力分布有较大的影响,有限元分析中应充分考虑螺栓预紧力的作用,常见的螺栓预紧力施加方法有[8-9]:
(1)初始穿透法。预先给螺栓与车轮一定的接触穿透量,分析中通过接触反力来实现螺栓的预紧。
(2)降温收缩法。给螺栓设置温降条件,使螺栓在温度变化过程中发生收缩,从而产生预紧效果。
(3)断面加力法。把螺栓截面进行打断,在两个断截面直接施加大小相等,方向相反的螺栓预紧力。
其中,法(1)和(2)是预加位移法,法(3)是预加力法。在螺栓预紧过程中,不但车轮发生了变形,螺栓本身也发生了变形,车轮与螺栓之间的相对变形在有限元分析之前是很难估算出来的,因此当采用法(1)和法(2)时,需反复试算和调整螺栓初始位置,直至螺栓所产生的预紧力大小接近实际预紧力。法(3)虽然可直接施加预紧力进行分析,但在车轮实际变形过程中,螺栓所受拉力是变化的,即螺栓内力并不总是等于预紧力大小,因此当螺栓受力变化较大时,法(3)产生的误差也会较大。本算例采用法(1)进行螺栓预紧,根据螺栓直径建立近似同等大小的螺栓有限元模型,参照实际预紧力大小,通过多次计算,反复调整螺栓与车轮的初始相对位置,使螺栓初始拉力近似等于实际预紧力大小。
3.5 加载时间步设置
疲劳分析需要考察外力旋转一周车轮的应力变化情况,实际分析过程中,是用有限个加载时间步近似描述外力整个旋转周期。车轮形状和对称特性不同,一周内的加载时间步个数也不一样。如图2 车轮,共12 个风孔、4 个螺栓孔和4 个突起加强包。螺栓孔和加强包近似在同一圆周上,相当于在这一个圆周上循环出现了3 个特征:螺栓孔、有加强包区域和无加强包区域(8 个)。为了更好的获得这3 个特征的最大应力值,在外力旋转一周的时间内,加载时间步应为“8+4+4=16”的倍数个。同理,为了更好的获得风孔和风孔间的最大应力值,加载时间步应为24 的倍数个。综合以上,最少加载时间步数应为16 与24 的公倍数个,即车轮旋转一周至少要输出48 个时间点的应力值。
3.6 提交计算
不同求解器生成计算文件的方法不同,提交计算文件的方式也有不同。完成了有限元网格划分、单元属性分配、材料参数设定、边界条件施加、加载时间步设置等一系列主要步骤后,就可生成计算文件并提交计算。
4 应力分析结果合理性判断
由于车轮结构对称,外力循环对称,因此应力分析结果合理与否,可从以下几点进行判断:
(1)结构对称点的应力应具有循环对称性,最大应力值按结构的对称性循环出现。结构上4 个对称点的“应力-时间”变化曲线,可见4 个点的应力曲线形态相同,峰值在时间轴上交替循环出现,说明应力分布较合理,如图3 所示。在车轮旋转一周内,如果车轮上某点的应力值随时间没有明显的正弦或余弦曲线变化,则说明车轮在旋转过程中产生了颤动,这通常是由于计算模型设置不合理造成的,包括网格尺寸不对称、局部网格质量较差、螺栓预紧力不均、固定约束不对称等问题。
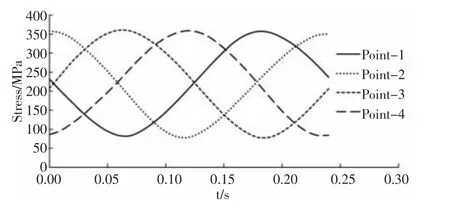
图3 对称点应力曲线形态相同Fig.3 Stress Curves Have the Same Shape on Symmetrical Points
(2)力F 作用点的位移大小应近似为一定值,否则说明车轮在旋转过程是跳动的,是不符合车轮实际运动状态的。如图4 所示,随时间t 的变化,力作用点位移近似呈一水平线,但当把曲线放大,发现其又略呈正弦曲线变化,这种微小的波动也正反映了车轮非完全轴对称的特性。
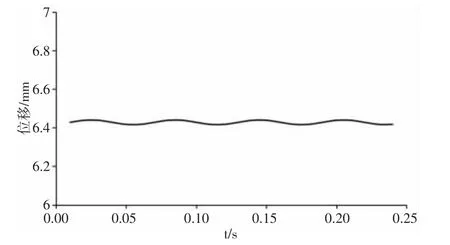
图4 力F 作用点的位移变化Fig.4 Displacement of Force Point
(3)由于S-N 曲线具有对数线性关系[8],即S 与N 具有一一对应关系,因此当采用任意一组材料的S-N曲线来进行疲劳寿命计算时,最小寿命位置和实测破坏点应是一致的,虽然此时疲劳寿命值与实测结果有可能不同。采用某近似材料S-N曲线对车轮进行疲劳分析后得到的最小寿命位置(螺栓孔附近,圆圈所示)和实测破坏点结果对比,可见,两者出现的位置基本一致,说明计算得到的应力结果和试验应力结果较为一致,如图5 所示。
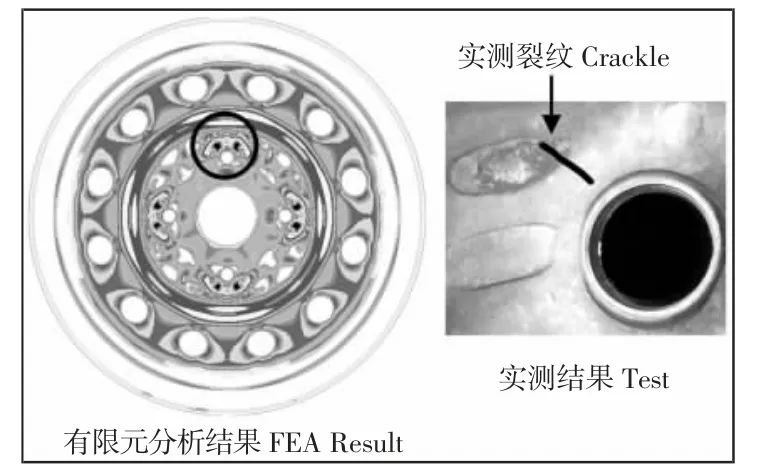
图5 有限元最小寿命位置与实测破坏点一致Fig.5 Crackle Points are the Same
5 疲劳分析过程
5.1 S-N 曲线的数学表达式
S-N 曲线是结构应力水平(S)与失效寿命(N)之间的关系式,一般认为当N 在(104~106)次范围时,S 与N 的关系式可用幂函数近似表示为[10-11]:

或用双对数曲线表示为:

式中:m 与C—与材料有关的参数,其中A=lg(C)/m,B=-1/m。
由表达式(4)可知,lg(S)与lg(N)呈线性关系,如图6 所示。当已知坐标值(lg(N1),lg(S1))及(lg(N2),lg(S2)),就可计算出A和B 的值,从而可近似确定S-N 曲线的表达式。
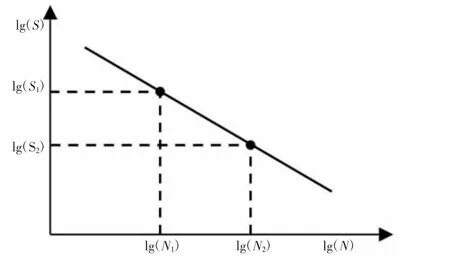
图6 S-N 曲线Fig.6 S-N Curve
5.2 试验过程与结果
试验过程车轮的安装状态,通过紧固件作用使轮辋内侧圆面紧贴于刚性试验台上,刚性弯矩力臂倒插于试验台中部镂空位置,车轮与弯矩力臂采用螺栓进行连接(螺母扭矩为100N·m),试验台下部安装电机(转速为400r/min),用于驱动力臂产生旋转弯曲力,整个试验过程监控和数据采样由专门的试验机控制系统自动完成,如图7 所示。

图7 车轮试验Fig.7 Wheel Test
根据产品抽样试验要求,需分别用两个弯曲力F1和F2(其中,F1=1369N,F2=2054N)对车轮进行弯曲疲劳试验,每个弯曲力进行6 组,共12 组试验结果,如表1 所示。
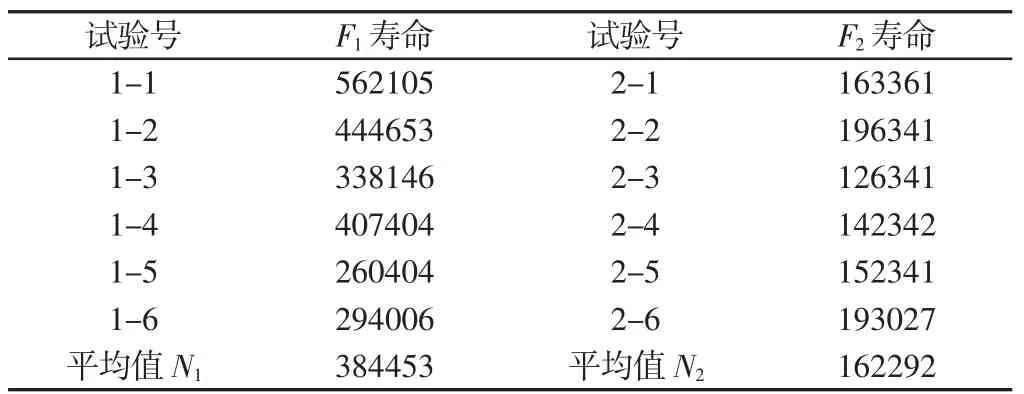
表1 车轮弯曲疲劳寿命次数Tab.1 Bending Fatigue Life of Wheels
由表1 可知,弯曲力相同,疲劳寿命却有较大的不同,说明试验结果具有分散性。事实上,影响疲劳寿命的因素很多,这种分散性在疲劳试验中是普遍存在的,因此产品同一批次的疲劳寿命不会是同一定值,而是落在某一带宽范围内的区间值。经观察表1 数据发现,虽然实测数据点有一定的波动性,但测试结果基本遵循了“弯曲力越大寿命越小”的规律,说明试验结果具有一定的稳定性和可靠性。在此,可取弯曲力相同的试验寿命平均值N1和N2近似作为结构分别对应于外力F1和F2的寿命值,即在力F1及在F2的作用下,车轮的平均寿命分别为384453 次和162292 次。
通常材料S-N 曲线试验比较耗时耗力,目前能获得的(商业疲劳软件材料库)为数不多的材料S-N 曲线,大多都是软件开发商收集或通过原材料标准样件测试而得。辐板式钢制车轮是经过金属板料塑性加工而成,实际产品材料力学性能相对原材料有较大的不同,车轮疲劳试验加载方式、结构尺寸与标准材料样件测试方法也不同,因此要获得车轮实际的材料S-N 曲线是比较困难的,如何获得车轮潜在的S-N 曲线是准确预测车轮寿命的关键。
5.3 S-N 曲线近似预测
S-N 曲线中的S 指的是应力幅值,有限元分析结果输出的通常是某点的应力值,而不是应力幅值。基于有限元分析结果,借助疲劳分析软件,选定某个强度极限与车轮材料相近的金属材料S-N 曲线,如表达式(5),就可算出结构上某点对应于该材料的寿命值N,再把N 代入表达式(5),就可反算出该点的应力幅值S。
lg(S)=3.6507-0.2lg(N) (5)
现参照表1 的试验结果,对同一款车轮分别做了F1及F2两种外力作用下的有限元应力分析,并采用式(5)的S-N 曲线表达式,在MSC.Fatigue 疲劳分析系统中进行疲劳寿命分析。由分析结果可得在F1及F2作用下结构的最小寿命分别为105.36次和105.18次,由此得到方程组:

从而求得lg(S1)=2.5788,lg(S2)=2.6146,即F1及F2作用下结构最小寿命点的应力幅值分别为102.5788=379.2MPa 和102.6146=411.7MPa。现把表1 的数据N1、N2,及以上求得的lg(S1)、lg(S2)分别代入式(4),可得方程组:


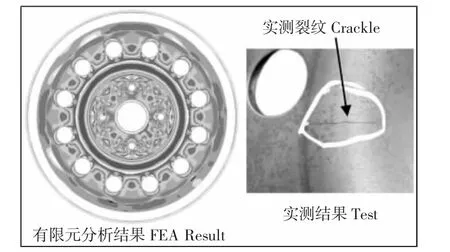
图8 S-N 曲线预测效果验证Fig.8 Verification of Prediction Effect of S-N Curve
进一步求得A=3.1122,B=-0.0955,由此可得车轮材料S-N曲线近似表达式为:现用表达式(8)去预测某款材料牌号相同、结构相近的车轮疲劳寿命,与试验结果对比,如图8 所示。可知有限元分析得最小寿命在轮辐顶上,和实测破坏点位置一致。此时有限元分析得到车轮寿命为14.1 万次,实测车轮平均寿命为12.6 万次,有限元寿命分析结果落在车轮实测数据区间内(9.5~17.3 万次),认为有限元寿命预测结果具有一定的可靠性。
6 结论
详细介绍了用有限元法模拟薄壁钢制车轮弯曲疲劳试验的方法和过程,得到以下结论:
(1)由于为薄壁结构,不宜采用减缩积分单元,可采用全积分六面体单元,单元长高比不宜太大,最好控制在1.5:1 以内,且结构厚度方向单元个数不能低于两层。
(2)应采用材料“真应力-应变”曲线进行计算。
(3)应考虑螺栓预紧力的作用,常见的螺栓预紧力施加方法有初始穿透法、降温收缩法和断面加力法等。
(4)为了更好的获得车轮应力分布,计算加载时间步个数应根据车轮螺栓孔、风孔、加强筋等特征的分布状态来设定。
(5)可对应力分析结果合理与否进行判断:结构对称点的应力应是循环对称出现;加载点位移应近似为一定值;如有试验结果,采用任一条S-N 曲线进行疲劳分析得到的最低寿命点位置应和试验结果一致。
(6)以车轮疲劳试验结果为参照,结合S-N 曲线数学表达式,可近似预测车轮潜在的材料S-N 曲线,基于此S-N 曲线去进行疲劳分析,可获得较合理的寿命结果。
