改进的多变量极限学习机在滚动轴承故障预测中的应用

王鸣明，李凌均，张炎磊，汪一飞

（郑州大学振动工程研究所，河南 郑州 450001）

1 引言

滚动轴承是旋转机械重要组成部分，其运行状况直接影响到整台机器的安全运行。在旋转机械的各种故障中，约有30%是由滚动轴承的故障引起的[1]。因此预测滚动轴承故障是十分必要的。佐治亚理工学院教授Vachtsevanos 把预测方法分为3 类，基于物理模型的预测方法，基于概率模型的预测方法和基于数据驱动的预测方法[2]。在机械故障诊断领域中，Matej Gasperin 等采用随机动态建模方法对齿轮剩余寿命进行预测[3]。文献[4]以单自由度系统形式对滚动轴承进行建模成功预测了轴承剩余寿命。文献[5]将小波相关排列熵和隐马尔可夫模型相结合，有效的预测了滚动轴承故障发生的概率。

极限学习机（extreme learning machine，ELM）是由文献[6]提出的单隐含层前馈神经网络算法。具有泛化学习能力强、训练速度快等优点，已成功应用于机械故障诊断领域。文献[7]将灰狼优化算法用于改进极限学习机，实现滚动轴承的故障分类。文献[8]提出了一种基于主成分分析和多变量极限学习机的轴承剩余寿命预测方法。文献[9]将粒子群算法与核极限学习机结合，用于磨煤机的故障诊断。

目前极限学习机多用于滚动轴承寿命预测，对于故障类型的预测则相对较少。而预测故障类型，就需要对振动信号的频谱结构进行分析。由于不同方向测得的振动信号存在差异，导致频谱结构也会出现差异。文献[10]提出的全矢谱技术可以融合同源多通道信号，为频谱的分析和预测提供了基础。文献[11]提出基于奇异值分解的极限学习机多变量时间序列预测方法，能够在不破坏多变量序列结构的前提下进行预测。由于各振动频率的幅值之间存在相关性，传统的多变量极限学习机将各个输入向量分开预测，忽略了多变量间的内部联系。运用奇异值分解和极限学习机相结合的方法，构建滚动轴承频谱预测模型。试验结果表明该方法能有效的对滚动轴承的频谱进行预测。

2 极限学习机

极限学习机（Extreme learning machine，ELM）是单隐层神经网络的算法，与传统神经网络相比，不需要人为设置大量的网络训练参数，网络的输入权值以及隐藏神经元的偏置随机给定，计算量和时间复杂度小。已成功应用于时间序列预测、模式识别、故障诊断等领域。其结构，如图1 所示。

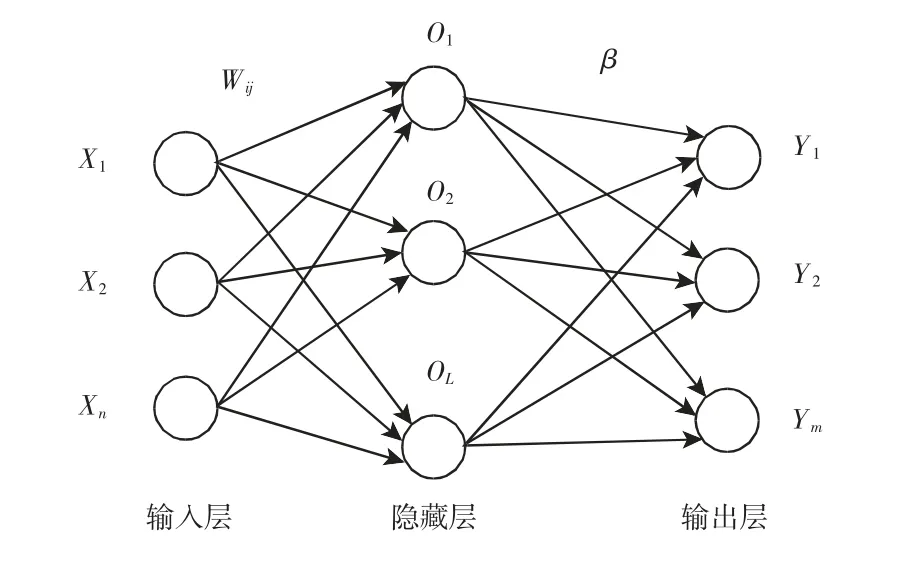
图1 ELM 预测结构Fig.1 ELM Prediction Structure

式中：H—隐藏层输出矩阵；β—输出权重矩阵；T—期望输出。

在ELM 算法中，输入权重wi和隐藏层单元偏置会被随机确定，隐藏层输出矩阵H 也就唯一确定。训练ELM 相当于求解线性方程组Hβ=T。求得输出权重β 为：

式中：H+—隐藏层输出矩阵H 的Moore-Penrose 广义逆矩阵。

3 SVDMELM 算法

假设有N 个样本，其中，第i 个样本输入矩阵为：

式中：m—嵌入的时间维度。输出样本矩阵为Y=［y1，y2，…，yN］。建立SVDMELM 模型为：

式中：W=［W1，W2，…，WL］—输入层与隐藏层的连接权重；B=［B1，B2，…，BL］—隐藏层神经元的阈值矩阵；Bi=［Bi，Bi，…，Bi］T（i=1，2，…，L）。—H（Xi）的第一左奇异向量；βl×m—奇异值分解层与输出层连接权重。

训练SVDMELM 相当于求解线性方程组Y=Hβ。求得输出权重为：

式中：H+—隐藏层输出矩阵H 的Moore-Penrose 广义逆矩阵。

SVDMELM 的结构，如图2 所示。与ELM 网络相比，在隐藏层与输出层之间添加了奇异值分解层。

图2 SVDMELM 预测结构Fig.2 SVDMELM Prediction Structure

4 实例分析

全寿命滚动轴承振动信号实验数据来自美国国家宇航局（NASA）网站，由辛辛那提大学智能维护中心提供。实验台共有4个滚动轴承（型号为Rexnord 公司的ZA-2115 双列圆柱滚子轴承），传动轴转速为2000r/min。每个轴承的同一截面相互垂直方向安装了PCB 353B33 加速度传感器。采样频率为20khz，采样间隔10min，每组数据共采样20480 个点。

图3 实验装置图Fig.3 Experimental Setup Diagram

从全寿命滚动轴承振动信号数据中取120 组双通道数据（各组数据时间间隔相等，包含正常到深度故障状况的数据）。对每一组数据进行奇异值降噪处理，然后通过全矢方法融合双通道数据得到其频谱，取其前800 个频率作为输入变量。具体预测流程如下：

（1）数据提取与预处理：提取X 通道和Y 通道全寿命振动信号120 组，包含正常到深度故障状况的数据。对信号进行降噪处理。

（2）信号融合：通过全矢谱技术融合X 通道和Y 通道信号。得到120 组信号的的全矢谱。

（3）取前800 个频率作为输入变量，利用滑动窗口法构建训练集和测试集。窗口内的数据作为训练集或测试集的输入样本，窗口外的下一组数据作为输出样本。窗口的嵌入维度m 为8。

（4）根据式（7）计算每个训练样本的特征样本Htr，对其进行奇异值分解。取其最大特征值和第一右奇异向量。

（5）计算每个测试样本的特征样本Hts，对其进行奇异值分解。取其最大特征值和第一右奇异向量。

（6）根据式（9）计算H??_tr 和H??_ts。根据式（11）计算β。（7）计算Y=Htsβ。输出预测结果。

提取其中内圈故障的一组双通道数据，采样频率为20KHz，采样点数20000 点。其故障特征频率为f=294Hz，转频为fr=33Hz。得到X 方向和Y 方向的频谱图及全矢幅值谱图，如图4 所示。

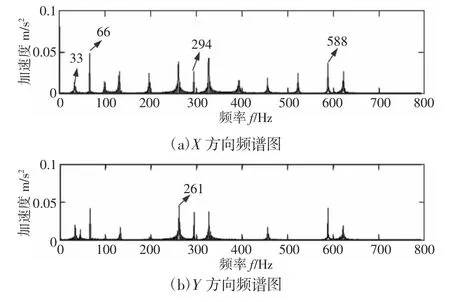
图4 X 和Y 方向频谱图和全矢谱图Fig.4 X and Y Directional Spectrograms and Full Vector Spectrograms

由图4 可以看出全矢频谱图融合了X 方向和Y 方向的频谱，不仅特征频率更加全面，而且特征频率处的振动幅值更加明显。用全矢谱作为训练数据避免了信息的遗漏，能够提高SVDMELM 预测的准确性。

分别采用ELM 和多变量SVDMELM 模型对滚动轴承3 的频谱进行预测，网络的隐藏层节点为100，输入输出节点为800，激活函数为Sigmoid 函数。它们的预测频谱，如图5 所示。从图5可以看出SVDMELM 方法预测的频谱比ELM 方法更接近实际频谱。为更加准确的比较ELM、SVDMELM 两种预测方法的优劣，采用均方根误差作为预测性能的评价指标，简记为“RMSE”。

图5 实际和预测频谱图Fig.5 Practice and Predictive Spectrograms

记录了两种预测方法在33Hz、66Hz、261Hz、294Hz、588Hz共5 个变量处的RMSE 值，实验次数为20，如表1 所示。由表1可知SVDMELM 方法在5 个主要频率点的均方根误差均小于ELM 方法。说明SVDMELM 的预测频谱更接近实际频谱，证明了方法的有效性。

表1 不同算法预测结果Tab.1 Prediction Results of Different Algorithms

5 结论

提出了基于奇异值分解和多变量极限学习机的方法，通过全矢谱方法对实验数据进行预处理，提高了样本的全面性。当多个变量之间存在联系时，由于SVDMELM 方法采用矩阵输入形式，并且运用SVD 方法对输入样本进行处理，能够保留多变量间的内部联系，提高预测精度。实验结果表明SVDMELM 方法比ELM 方法更适用于滚动轴承的频谱预测。