转子偏斜角不对中对滑动轴承系统运行稳定性的影响

葛原珲，徐武彬，李 冰，魏晋鹏

（广西科技大学机械工程学院，广西 柳州 545006）

1 引言

现阶段滑动轴承凭借其承载能力大，旋转精度高等优点被广泛应用于工程实际中，故滑动轴承系统的运行稳定性是影响旋转机械设备安全运转的重中之重，且研究针对转子形位误差对其轴承系统运行稳定性影响一直是转子动力学领域内的关键问题之一。而在文献[1]通过实验观察发现转子不对中可以被认为是继转子动不平衡后的常见的故障。但这并没有引起相关研究人员的足够重视。文献[2]使用“不对中”一词来表示由于不同物理过程而导致的转子与轴承中心轴线出现偏差的现象，并对各种的转子不对中的现象进行分析。现如今根据各类文献以及大量故障实例得出转子不对中误差是指轴瓦与轴颈之间存在角度错位的现象，即是指基于轴瓦和轴颈的中心轴线在相互不平行的情况下，轴颈的中心轴线在沿着轴瓦中心轴线所在的水平面内和垂直于该水平面的竖直平面内分别存在一个摆动角和偏斜角，其角度不同，导致转子不对中误差的程度也不同。而该误差的存在将会导致润滑油油膜厚度的急剧减小，其中的润滑油膜则是保持发生相互挤压或相互运动的两表面不会直接接触的原因。而油膜厚度的降低，会很大程度上改变轴承内部原有的压力场以及温度场[3]，且存在转子不对中误差的滑动轴承内部的最大油膜压力会远高于正常情况下的滑动轴承，产生较为严重的边缘载荷。由于转子不对中误差程度的不确定性，进而可能会发生油膜破裂，导致轴承的内部磨损，例如划伤，严重影响其承载性能[4]。因此，分析滑动轴承转子系统运行稳定性时考虑转子不对中误差对其稳定性的影响显得尤为重要。

现有文献更集中于研究考虑转子不对中存在时滑动轴承系统的动态特性和润滑特性。文献[5]通过仿真的方法提出了不对中转子的动态特性。文献[6]通过建立数值模型分析可倾瓦轴承与内部转子发生角度偏差的原因。文献[7]分析了考虑垂直方向上转子不对中滑动轴承的动态性能。文献[8]建立有限元模型对转子系统动态响应的频谱成分进行分析，进而得到判断转子不对中故障的诊断信息。文献[5-8]均是研究了考虑转子不对中时滑动轴承系统的动态特性。文献[9]通过试验分析了轴受载荷状态下引起的轴颈倾斜对滑动轴承润滑特性的影响规律。文献[10]研究了转子偏差角度对气体静压轴承内部气膜压力分布的影响。文献[11-12]均使用有限差分法计算雷诺方程获得油膜压力，并进行分析得到了转子不对中对滑动轴承稳态油膜润滑特性的影响规律。但均未能进一步表征转子不对中误差对轴承系统运行稳定性等特性的影响规律。

建立了计入转子偏斜角误差的滑动轴承系统动力学模型，并提出对其非线性动力学分析以及计算方法，进而研究不同程度转子偏斜角误差对系统基于Op参数的运行稳定性等特性所造成的影响。

2 滑动轴承油膜力模型及计算方法

2.1 计入转子偏斜角误差的滑动轴承系统动力学模型及油膜厚度

一刚性理想圆转子滑动轴承系统的油膜力模型，如图1 所示。

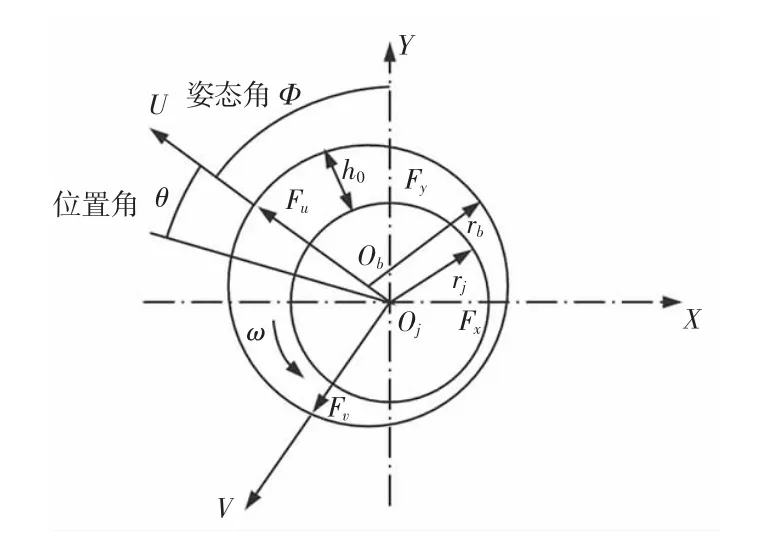
图1 理想圆轴颈滑动轴承系统动力学模型Fig.1 Dynamic Model of Symmetric Rigid Journal Bearing System

其中，轴瓦的轴心为Ob，轴颈轴心为Oj。Ob与Oj之间的距离即为偏心距e，rb和rj分别表示轴瓦和轴颈的半径，h0代表任意处油膜厚度，当其处于稳定运行状态时，由滑动轴承的结构参数及其位置角θ 姿态角Φ，以及余弦定理可推导出图1 中滑动轴承内部任意位置的油膜厚度h0：

式中：c—滑动轴承的轴间间隙，即c=rb-rj；

代入式（1）得：

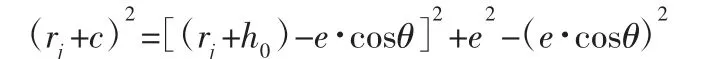
化简得：

通过观察和验算可得，滑动轴承的偏心距e 相比其轴颈半径rj而言在数量级上微乎其微，故将式（2）中e2与（ecosθ）2两项略去，其中，ε 为滑动轴承的偏心率，ε=e/c 代入化简得：

在其基础上建立带有轴颈偏斜角误差的滑动轴承转子油膜力模型，如图2 所示，其中Z 轴为轴承中心线，Ob为轴瓦的圆心，轴瓦的半径为rb，轴承长度为L，轴颈的半径为rj，图中的Y 轴坐标轴所在的位置为轴瓦长度的L/2 截面处，则点Oj2即为该截面的轴颈中心，该滑动轴承转子系统的初始偏心距为|ObOj2|=e，图中Oj1和Oj3则分别是轴瓦首端和末端两截面轴颈的圆心，图中θ 和Φ 分别为转子系统处于稳定工作状态时的位置角和姿态角，表示转子不对中误差偏斜角的角度。h 为轴瓦和轴颈间实际油膜厚度。而当滑动轴承内部转子偏斜角存在时，即存在转子不对中误差时，如图2 所示，需要用角对转子不对中误差进行表征，首先沿滑动轴承轴向等距离的插入节点i，将计算区域沿轴向分为均等的m 份，则每份的长度为L/m，由几何关系可得顺沿轴颈轴向的任意截面中心处距离轴瓦中心的偏心距ei。

图2 计入转子偏斜角误差的滑动轴承系统动力学模型Fig.2 Dynamic Model of Hydrodynamic Journal Bearing System with Deflection Auglar Error

其中，i=1，2，3，…，m+1；

将（4）式中偏心距ei代入（3）式化简得到任意截面的油膜厚度计算式（5）：

通过（5）式即可计算得到带有偏斜角误差滑动轴承系统中任意截面位置的油膜厚度，式中：i=1，2，3，…，m+1。

如图1 所示作用在轴颈的非线性油膜力与轴颈自身的运动状态和位置有关，利用有限差分法，求解描述润滑油膜压力变化的表达式（6），即Reynolds 方程，进而确定油膜压力，再通过式（7）积分计算求解作用在轴颈上的瞬时油膜力分量[12]，即FU和FV。

式中：p—油膜压力；x 和z—轴承的径向和轴向；μ—油膜的流体动力学粘度；t—时间。

式中：FU和FV—U 和V 方向上的油膜力；p—油膜压力；θ—位置角。图1 中Fx与Fy则分别为FU和FV在水平、竖直方向上的油膜力分量。

2.2 转子系统承载特性

这里所述的滑动轴承转子系统为水平安装，当系统处于稳定运转状态时，即水平方向上油膜力为Fx=0，则此时竖直方向上的油膜力Fy则表征该滑动轴承系统的承载能力。引用了无量纲参数Sommerfeld 数，来表征转子系统动态特性与其稳定性的关系。Sommerfeld 数的计算公式为[13]：

式中：μ—流体的动力学粘度（Pa·s）；N—转速（r/min）；L—滑动轴承的长度（m）；rj、Db、c—轴颈半径（m）、轴瓦直径（m）以及轴承间隙（m）；F—轴承的载荷（N），当系统处于稳定状态时，F即为Fy。

2.3 转子系统运行稳定特性

针对滑动轴承系统临界转速的确定直接采用了对数衰减率方法[14]进行计算与判定。与此同时，为了描述倾斜角误差对该滑动轴承系统运行稳定性的影响，引入了无量纲运行参数Op，并结合该转子系统的稳定性临界转速，通过计算无量纲运行参数Op进而可以表示滑动轴承系统的运行状态。其中运行参数Op可以表示为[15]：

式中：F—轴承载荷；m—转子系统质量，ω 则为系统的稳定性临界转速。

3 转子偏斜角不对中误差对滑动轴承系统工作特性的影响

3.1 偏斜角不对中误差对轴承油膜厚度的影响

所采用的滑动轴承系统各项参数，如表1 所示。依次展示了偏斜角为0°、0.015°、0.03°以及0.05°即具有不同程度的转子偏斜角误差下的滑动轴承系统油膜厚度的变化情况，如图3 所示。与此相对应，不同程度的转子偏斜角误差对其油膜压力峰值变化的影响，如图4 所示。

表1 滑动轴承系统参数表Tab.1 The Parameters of Hydrodynamic Journal Bearing

不同程度的偏斜角误差对滑动轴承系统油膜厚度的影响，如图3 所示。通过对比图3（a）到图3（d）中可以看到，当顺沿轴承轴向时，油膜厚度数值随着转子偏斜角的逐渐增大而产生显著的变化，即偏斜角度的增加将导致滑动轴承系统内部油膜厚度分布的不均匀化更加严重。而相对于理想圆轴颈如图3（a），即使存在0.03°的转子偏斜角误差如图3（c），就导致该轴承系统中最小油膜厚度由1.39×10-4下降至1.02×10-4，即下降了26.6%，且偏斜角增加至一定程度后，如图3（d）中可以看到最小油膜厚度几乎为0，且通过对比图3（a）到图3（d）也可以看到随着偏斜角误差的增加，使得该轴承轴向油膜厚度的峰-峰值增大，这都是在实际情况中应极力避免的。

图3 转子偏斜角误差影响下的油膜厚度Fig.3 Oil Film Thickness with Influence of Deflection Angular Error

不同程度偏斜角误差对滑动轴承系统中油膜压力的影响，如图4 所示。在图4（d）中可以看到转子偏斜角误差存在对滑动轴承系统中油膜压力分布产生了显著的影响，且通过对比图4（a）到图4（d）同样可以看到随着偏斜角误差的增加，使得该轴承系统中油膜压力场沿轴承轴向逐渐由单个波峰进而形成双波峰，且波峰所在的位置会随着偏斜角误差的增加而逐渐沿轴向向轴承两端移动，而此时油膜压力场峰值则随着转子偏斜角误差的增大而增加甚至进而产生畸变。

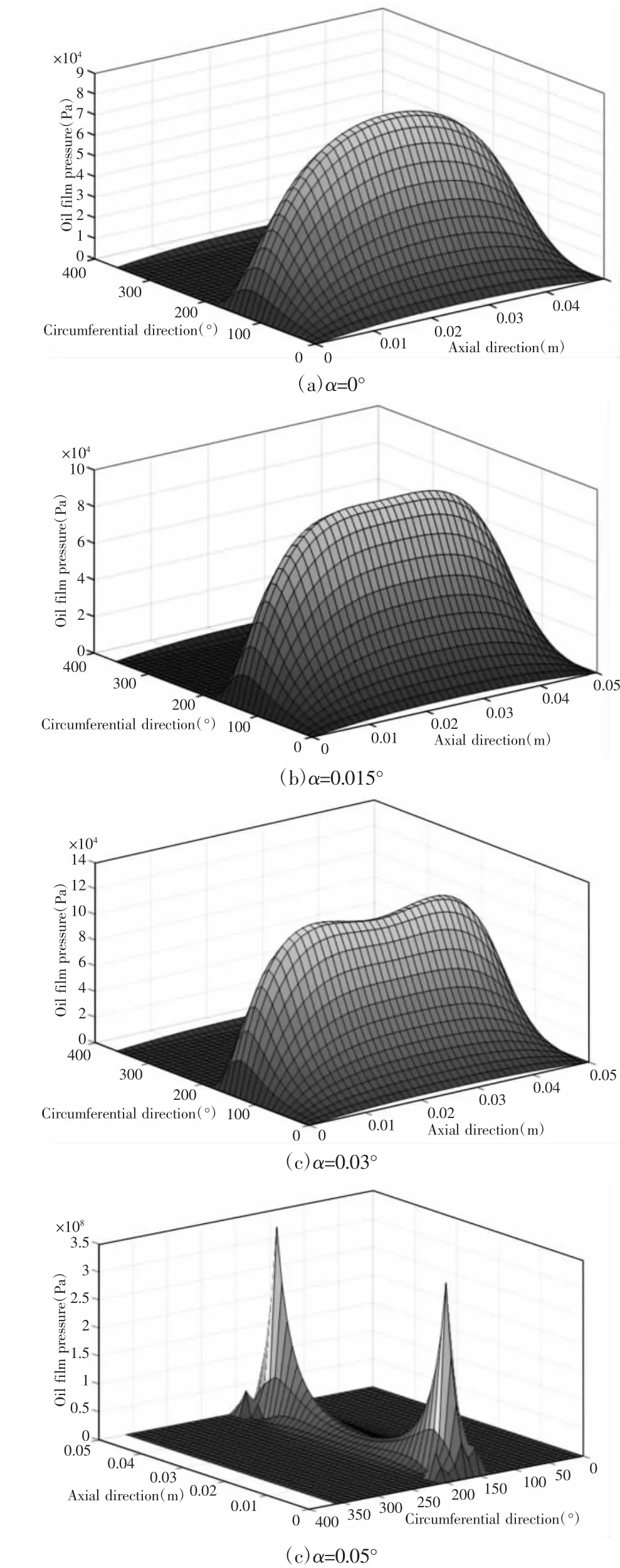
图4 转子偏斜角误差影响下的油膜压力Fig.4 Oil Film Pressure with Influence of Deflection Angular Error

3.2 转子偏斜角度误差对轴承承载能力的影响

对于Sommerfeld 数的计算以及定义均在上述文中上述部分明确给出，Sommerfeld 数是描述滑动轴承系统承载能力的重要参数之一，同时与轴承自身结构参数密切相关，即对滑动轴承结构设计起到了至关重要的作用。

图5 不同偏斜角误差下Sommerfeld 数与偏心率的关系Fig.5 The Relation Curves of Eccentricity Ratio and Sommerfeld Number Under Different Degreesof Deflection Angular Error

在不同程度的偏斜角误差下，该轴承系统Sommerfeld 参数处于不同偏心率时的变化情况，如图5 所示。展现了在不同程度的转子偏斜角误差影响下轴承承载力的变化规律，从图5 中可以看到随着转子偏斜角误差角度的不断增加，Sommerfeld 数曲线则呈现有向左偏移的情况，即Sommerfeld 数随着偏斜角度误差的增大而减小，这一结果表明转子偏斜角度误差的增加在一定程度上使得轴承系统的承载力得到了提高。

3.3 转子偏斜角误差对轴承系统运行稳定性的影响

为更好地研究转子偏斜角度误差对该滑动轴承系统运行稳定性的影响，故引入了能够表示滑动轴承系统运行状态的无量纲参数Op，该滑动轴承系统在不同程度的转子偏斜角误差影响下Op参数与其偏心率关系的稳定性曲线，如图6 所示。

图6 不同偏斜角误差下Op 参数与偏心率的关系Fig.6 The Relation Curves of Eccentricity Ratio and Op Parameter Under Different Degrees of Deflection Angular Error

从图6 中可以看到，在偏心率ε≤0.6 时，该稳定性曲线随着转子偏斜角误差的增加而向上偏移，表明在该偏心率范围内，轴承系统中转子的临界转速随着自身偏斜角误差的增大而减小，即在偏心率ε≤0.6 的范围内，转子偏斜角误差的存在不利于轴承系统的稳定运行，即此时随着转子偏斜角误差的增大，将导致轴承系统的运行稳定性进一步下降。但从图6 中同样可以看到当偏心率ε＞0.6 时，该图中的稳定性曲线将随着转子偏斜角的存在而向下偏移。但是，当偏心率ε＞0.6 时，该轴承系统内部润滑油的粘度偏低，使得图6 中横坐标偏心率ε＞0.6 处的范围为不稳定区域。

3.4 转子偏斜角误差对轴承系统摩擦功率损耗的影响

在轴承系统运行状态下，轴颈旋转将受到润滑油与轴瓦内表面摩擦阻力的影响，导致滑动轴承系统出现摩擦功率损耗。其占据了整个轴承系统能量损失的主要部分，故降低摩擦功率损耗，提高工作效率是轴承系统设计工作重要环节之一。轴承系统运行稳定状态下摩擦功率损耗的计算公式如下所示[16]。

式中：μ—油粘度，单位：Pa·s；L—轴承长度，单位：m；Vτ—系统稳定状态下的轴颈表面切向速度，单位：m/s。

图7 转子偏斜角误差轴承系统摩擦功率损耗与偏心率的关系Fig.7 The Relation Curves of Eccentricity Ratio and Friction Power Loss Under Different Degrees of Deflection Angular Error

在稳定状态下，在不同程度转子偏斜角误差影响下，轴承系统摩擦功率损耗与偏心率的关系，如图7 所示。从图7 可以看到当偏心率ε＜0.65 时，轴承系统的摩擦功率损耗随着偏心率的增加而减小，且偏心率ε 处于（0.2～0.3）之间时，该轴承系统的摩擦功率损耗最大，而在偏心率固定的情况下，摩擦功率损耗曲线则随着转子偏斜角误差增加向下偏移。但当偏心率ε＞0.65 时，滑动轴承系统稳定状态下的摩擦功率损耗曲线则随着转子偏斜角的增加而向上偏移。

4 结论与展望

4.1 结论

所得到的结论如下：

（1）建立了带有转子偏斜角不对中误差的滑动轴承系统动力学模型，并基于Sommerfeld 数建立了转子偏斜角不对中误差对滑动轴承系统润滑特性，承载特性以及稳定性等工作特性的影响关系。

（2）转子偏斜角误差的存在对滑动轴承系统中油膜厚度以及油膜压力的变化均产生明显的影响，随着转子偏斜角误差的增大使得油膜厚度分布的不均匀化更加明显，导致其油膜厚度最小值近一步减小。而随着偏斜角误差增大，使得滑动轴承系统中油膜压力峰值呈现增加的趋势，油膜压力峰值由单波峰逐渐出现双波峰且波峰位置不断沿轴向向轴承两端边缘偏移，使轴承内部油膜压力分布边缘化，加重了油膜压力分布不均匀化的程度。是导致发生油膜破裂，轴承与转子相接触产生磨损的主要原因之一。

（3）转子偏斜角误差的存在且逐渐增大时使轴承系统的承载能力得到了一定的提高。

（4）当偏心率ε≤0.6 时，转子偏斜角不对中误差的存在和增加都将使得滑动轴承系统的运行稳定性进一步降低。当偏心率

ε＞0.6 时，由于轴承系统内部润滑油粘度偏低，使得该范围为不稳定区域，故当偏心率ε＞0.6 时，转子偏斜角误差对系统稳定性的影响具有不确定性。

（5）当偏心率ε＜0.65 时，稳定状态下的滑动轴承系统摩擦功率损耗随着转子偏斜角误差的增加而减小。当ε＞0.65 时，转子偏斜角误差的增加则使得稳定状态下的滑动轴承系统摩擦功率损耗增大。

这里的研究结果可以使机械设计人员更加清晰的了解转子偏斜角误差对滑动轴承系统运行稳定性的影响，在滑动轴承的设计阶段时使机械设计人员通过选择合理的偏心率范围或者通过提高装配精度，来避免或者减弱转子偏斜角误差对滑动轴承系统所造成的不良影响，进而可以使滑动轴承系统的设计方案更好的满足实际工作需求。

4.2 展望

转子不对中误差包括竖直方向上转子的偏斜角误差以及水平方向上转子的摆动角误差，而由于机械加工制造误差以及装配误差的存在，以及制造成本的限制，转子不对中误差难以完全避免，而只能通过特殊的加工或装配方法进行选择性的误差补偿，通过对转子偏斜角误差的研究结论可知，后续对于转子水平方向上的摆动角误差以及偏斜角、摆动角同时存在的组合误差对于滑动轴承系统运行稳定性影响的研究更显得尤为重要。