基于响应面法的动力电池包箱体轻量化优化设计
2021-03-05欧阳威王丽娟陈宗渝曾泽江
欧阳威,王丽娟,陈宗渝,曾泽江
(南昌大学,机电工程学院,江西 南昌 330031)
1 引言
电动汽车市场竞争加剧的现状驱动着汽车生产制造商谋求关键核心技术的突破,旨在为消费者提供安全性更高、续航里程更长、综合体验更佳的电动汽车产品。动力电池包箱体作为电池模组的保护罩、承载体,关乎着内部动力电池能否正常运行,其结构必须满足电动车在正常或复杂运行工况下一定的刚度与强度等硬性要求,如何设计出一种高强度、轻量化的电池包箱体对于保障整个动力电池的安全性、提高热管理效率以及增加电动车续航里程具有重要意义[1]。
鉴于动力电池模组均由一定规格的高密度电池单体通过串并联成组,电池包的轻量化空间主要集中在箱体上,实现电池包箱体轻量化的有效途经主要有:采用拓扑优化、尺寸优化、形貌优化和形状优化等结构优化方法;使用轻量化材料;利用先进的成型工艺等[2]。精确的有限元模型是结构响应预测和结构优化的必要条件[3],结合有限元仿真技术并基于响应面法的优化设计,可方便地通过有效的试验设计手段将设计变量与结构响应之间的关系以多项式回归方程的形予以表达,经统计学原理修正并检验响应面模型满足一定的精确度与有效性后能较好的完成对设计响应的平顺,在工程上得到了广泛应用,后续将沿用并拓展此类方法对电池包箱体进行轻量化优化设计。
2 电池包箱体动静态特性有限元分析
电动汽车在实际行驶过程中,电池包受到的交变载荷较为复杂,其箱体结构能否满足动静态性能要求将直接影响内部电池模组和电气连接的安全性,运用有限元法了解电池包箱体的动静态特性发现原设计方案的不足,从而为后续优化设计奠定基础。
2.1 电池包箱体有限元模型的建立

图1 电池包简化3D 几何数模、安装位置及其有限元模型Fig.1 Simplified 3D Geometric Modeling,Installation Position and Finite Element Model of Battery Package
某款电动汽车动力电池包的三维CATIA 简化几何数模,如图1(a)所示。该动力电池包用8 个M12 螺栓固定于车身上、布置在地板正下方,如图1(b)所示。整个电池包呈现出较为规则的长方体外形,外轮廓尺寸为(934×566×155)mm,其主体结构包括上箱盖、下箱体、吊耳、下箱体支撑板及其连接件、电池模组、电气附件等,电池包箱体各部件母材材料均为Q235 钢。为了准确有效的模拟电池包箱体与电池模组的相互作用,在HyperMesh 中建立电池包箱体的有限元模型时将复杂的电池模组简化为一个较为规则的长方体引入,并采用均质化的六面体实体网格划分电池模组,这便保留了真实的力的传递路径,其余电池包箱体的各部件均采用壳网格划分,焊点连接按实际的焊点布置情况采用RBE2 单元模拟,最终建立的电池包箱体有限元模型,如图1(c)所示。单元总数为66187,节点总数为62247,经过合理配重使模型质量和质心与实际的吻合。
2.2 典型工况静强度与静刚度分析
路面颠簸工况、紧急制动工况和急转弯工况是车辆在道路上行驶时遇到的三种典型路面工况,结合典型的路面工况对电池包箱体的静强度与静刚度进行考核评估,考虑电动汽车实际运行条件,在MSC.Nastran 中进行有限元模拟分析时将按表1 所述的工况加载方式对整个电池包箱体施加惯性载荷,因电池包通过紧固螺栓与车体相连,为此约束施加在两侧吊耳的8 个螺栓区域,约束自由度为3 个平动自由度。

表1 电池包箱体典型工况与加载方式Tab.1 Typical Working Conditions and Loading Modes of Battery Case

图2 电池包箱体的等效应力云图Fig.2 Equivalent Stress Nephogram of Battery Case
经仿真分析,电池包箱体在典型路面三工况下的等效应力云图,如图2 所示。其中路面颠簸工况中下箱体的最大等效应力为228MPa,较接近其材料的屈服极限;急转弯工况中下箱体支撑板的最大等效应力为285MPa,超过其材料的屈服强度,久之有破坏风险;电池包箱体的位移云图,如图3 所示。其中路面颠簸工况中下箱体的最大变形量为1.91mm,说明下箱体中部为刚度薄弱区。在对动力电池系统做静力学分析时,一般要求电池包结构刚度应满足在1g 加速度工况下结构的最大变形量不应超过1mm,在3g 加速度工况下结构的最大变形量不应超过3mm[4]。不妨假设在1g 到3g 加速度范围内电池包结构的变形量与加速度呈现出线性关系,则在选择的典型路面三工况条件下,电池包箱体的最大变形量不应超过2mm。基于此,可判定电池包箱体原方案设计的静强度不满足要求,静刚度基本满足要求,需做进一步优化。
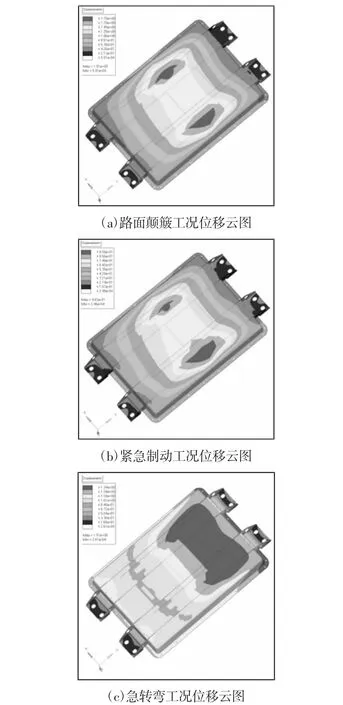
图3 电池包箱体的位移云图Fig.3 Displacement Nephogram of Battery Case
2.3 电池包箱体模态分析
电动汽车在道路上行驶时无时无刻不受到来自路面不平度产生的激励,路面激励经过车轮、悬架、车身传递到电池包,如果电池包结构的固有频率接近路面激励频率,则会存在共振风险,长此以往电池包存有安全隐患。由于来自路面不平度的激励矢量几乎是铅垂方向,为了提前规避掉共振风险,要求电池包结构的低阶铅垂向约束模态频率必须高于路面激励频率。按照电池包实际的约束情况施加边界约束,即约束两侧吊耳8 个螺栓区域3 个平动自由度,依据MSC.Nastran 求解的有限元分析结果提取了电池包箱体的前两阶约束模态振型,如图4 所示。第1 阶约束模态为箱体左右摆动振型,第2 阶约束模态为下箱体上下跳动振型,频率为19.18Hz,所以可能与路面激励产生共振的电池包箱体模态是从第2 阶开始的。该电池包所适配的电动车属于城市用电动车,参考城市道路行驶工况条件,其正常行驶速度一般不超过80km/h,城市道路属于平坦路面,路面不平度波长在(1.0~6.3)m区间范围[5]。通常路面激励频率与路面不平度波长、车辆行驶速度之间存在如下关系:

式中:μf—路面激励频率,单位Hz;λ—路面不平度波长,单位m;V—车辆行驶速度,单位km/h。
由式(1)可计算出与该电池包发生共振的路面激励频率最高约为22Hz,另考虑到路面激励经一系列传递后频响函数有所衰减的因素,实际传递至电池包的激励频率应低于计算所得,但为了保险起见,把电池包箱体结构的第2 阶约束模态频率的安全阈值设置为路面激励频率22Hz 为宜。由此可以判断电池包箱体原方案设计存有与路面激励发生共振的风险,需做进一步改进。

图4 电池包箱体约束模态振型Fig.4 Constrained Modes Vibration of Battery Case
3 基于响应面法的优化方法
3.1 多项式响应面近似模型
响应面优化方法是采用科学的数量化分析方法研究响应变量与输入变量之间的关系,通过合适的试验设计方案,获取某点附近一定规模数量点的实际响应值,建立一个用简单的函数关系近似替代实际的复杂仿真模型(即响应面模型),在充分靠近这个点的区域内用这个近似模型代替实际函数进行复杂计算,其拟合的精度和拟合效率将直接影响后续优化效果[6-7]。
工程应用中通常采用诸如1 阶或2 阶形式的低阶多项式回归模型来逼近真实的有限元模型,1 阶和2 阶多项式响应面近似模型的函数表达式分别为:
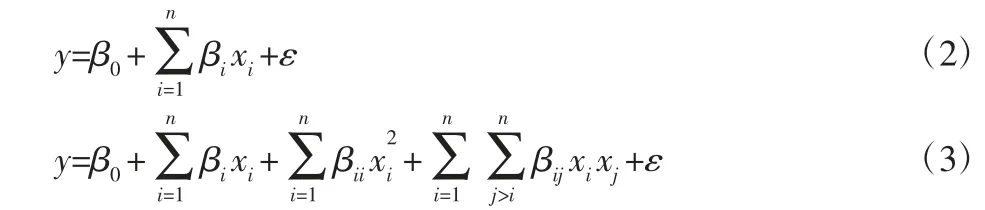
式中:y—预测响应;β0—常数项;βi—一次项系数;βii—二次项系数;βij—交互项系数;xi、xj—设计变量;ε—误差项。
3.2 多元回归分析与最小二乘估计
回归分析基于观测数据确定多个变量间的依赖关系,从而建立不同的回归模型并估计未知参数,通过对不同关系式的显著性检验选择合适的响应面模型。为了确定回归方程的待定系数需要根据合理的试验方案进行一系列试验次数不少于待定系数个数的独立试验,获得对应试验的响应值,又因响应面函数是性能函数的近似,根据响应面函数计算出的结果与试验所得响应值之间存在一个误差,为了使建立的响应面最接近所有的试验数据点,可通过利用最小二乘估计原理使其误差的平方和最小的途径实现[8-9],在求解多元方程组的同时也合理确定了待定系数,从而得到响应面函数。

式中:Y—响应矩阵;β—回归系数矩阵;X—设计变量矩阵;ε—误差项矩阵。
设b=[b1,b2,…,bk]T为β=[β1,β2,…,βk]T的最小二乘估计,则[b1,b2,…,bk]T满足使全部观测值yi与回归值yi1的残差平方和S 最小的要求,即:

将b=[b1,b2,…,bk]T代入可使式(5)取极小值的必要条件方程组(6)求解,即可求得式(7)所示的多项式系数的无偏估计。

式中:b0、bj—回归系数β0、βj的无偏估计;b—无偏估计阵;X—设计变量矩阵;Y—响应矩阵。
3.3 响应面质量评价


4 电池包箱体轻量化优化设计
4.1 设计变量
为了不变更电池包内部电池模组和电气附件的布置,从最经济的角度考虑,以电池包箱体各部件的厚度作为此次优化的设计变量,定义T1为上箱盖厚度,T2为下箱体厚度,T3为左右侧4个吊耳的厚度,T4为下箱体支撑板厚度,T5为支撑板连接件厚度,设计变量尺寸范围,如表2 所示。

表2 电池包箱体优化设计变量尺寸范围Tab.2 Variables Size Range for Optimum Design of Battery Case
4.2 目标函数与约束函数
通过对电池包箱体的动静态特性有限元分析可知,其原方案设计存在不足之处,为了使电池包箱体轻量化优化后满足动静态性能要求,考虑以电池包箱体在典型路面三工况下的最大等效应力σmax、最大变形量dmax和箱体结构的第2 阶约束模态频率μf以及箱体质量M(T)为设计响应,则轻量化优化时的数学模型表达式为:

式中:σI、dl—箱体在路面颠簸工况下的最大等效应力、最大变形量;σm、dm—箱体在紧急制动工况下的最大等效应力、最大变形量;σn、dn—箱体在急转弯工况下的最大等效应力、最大变形量;[σ]、[d]—箱体各部件材料的许用应力(取235MPa)、箱体在典型路面三工况下的变形量许用极限(取2mm);[μ]—由路面不平度引起的激励频率(取22Hz);T—设计变量矩阵。
4.3 建立拟合多项式响应面近似模型
4.3.1 Box-Behnken 试验设计
由于电池包箱体轻量化优化数学模型中引入的设计响应类型较多且穿插在目标函数与约束函数中,同时考虑到效率、设计区域与操作区域问题,在此选择Box-Behnken 试验设计(简称BBD)来拟合设计变量与响应之间的函数关系。BBD 是一类基于三水平不完全阶乘设计的可旋转或近似可旋转二阶设计,它把因子各试验点取在立方体棱中心,且所有试验点均在同一球面上[11-12],并未把所有试验因子同时置于高水平,对于试验区域较严格、因子水平较限制时相对有效。在Design-Expert 软件中利用BBD 进行5 个设计变量3 个水平试验设计时的设计因子及其水平编码情况,如表3所示。并根据表3 获得了46 个试验组合,进而按照BBD 安排的试验顺序依次开展箱体的动静态特性有限元分析,采集对应试验组合的各设计响应值得到构造响应面近似模型所需的设计矩阵。
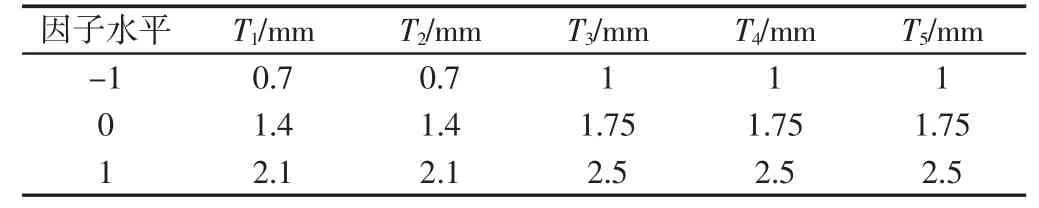
表3 Box-Behnken 试验设计因子及其水平编码Tab.3 Box-Behnken Design Factors and its Level Codes
4.3.2 回归方程的建立及有效性分析
通过对试验设计矩阵数据的多元回归分析、关系式未知参数的最小二乘估计以及回归方程的显著性检验,最终拟合得到了各设计响应的多项式回归方程,它们的函数关系表达式分别为:

各实际设计响应与模型预测响应奇偶检验图,如图5 所示。若是落在检验图对角线上或对角线附近区域的点越多,则表明所建立的响应面回归方程准确性越高,由图5 可知,拟合的各设计响应面模型的校验值基本上均紧邻检验图对角线,说明试验值与模型预测值之间具有较佳的拟合性。
采用帕累托方差分析对回归方程进行了显著性检验以及描述性统计分析以评价其有效性,结果如表4 所示。p 值为检验模型是否显著的有效工具,由表4 可知,所拟合的响应面模型均满足p<0.0001,表明模型高度显著;M(T)响应面模型的R2和均等于1 且MSE 很低,表明其精确度和可靠性极高;而其余3 个响应面模型的R2和均较接近于1,说明它们拟合出的回归方程质量较好,满足一定要求。

图5 各实际设计响应和模型预测响应奇偶检验图Fig.5 Parity Plots of Actual Design Responses and Model Predictive Responses

表4 响应面模型方差分析与质量评价Tab.4 Response Surface Models Variance Analysis and Quality Evaluation
4.3.3 轻量化优化与验证
将拟合有效的响应面模型代入电池包箱体的轻量化优化数学模型中进行迭代求解,得到设计区域内圆整后的最优组合为(T1,T2,T3,T4,T5)=(0.7mm,1.4mm,2.1mm,1.3mm,1.1mm),为了验证模型优化的准确性,根据最优组合设计试验进行有限元仿真验证,结果如表5 所示。由表5 可知,所得到优化方案的模型预测响应值与有限元仿真结果较为接近,相对误差较小,有较高的准确性,优化效果显著,不仅使箱体质量相比于原方案减少了7.4%,减重效果较理想,而且使箱体在典型路面三工况下箱体的最大等效应力降低了18.6%、最大变形量减小了22.5%,箱体结构的第2 阶约束模态频率提高了14.8%,箱体的动静态性能得到明显改善。

表5 优化结果与验证Tab.5 Optimized Results and Verification
为了避免电池包箱体轻量化后整体支撑刚性下降从而增加动力电池的碰撞安全风险,另需校核动力电池在碰撞工况下的安全性。由于电池包布置在前地板正下方,选择相对电池包危险系数较高的50km/h 侧面碰撞工况在Ls-Dyna 中进行电动车整车碰撞安全仿真以察看电池包在整车上的变形情况,侧碰过程中移动壁障与整车即将发生分离时整车最大变形图,如图6(a)所示。电池包主体在侧碰过程中整车最大变形时的位移云图,如图6(b)所示。侧碰仿真结果表明:来自移动壁障的冲击载荷主要由车体结构承受了而只有小部分传递至电池包,即使是侧面碰撞中整车变形最严重时,箱体侧壁也未接触到电池模组,内部电池模组未受到挤压,尚余安全空间,满足法规GB/T31498-2015 电动汽车碰撞后安全要求中对REESS 移动要求的规定。

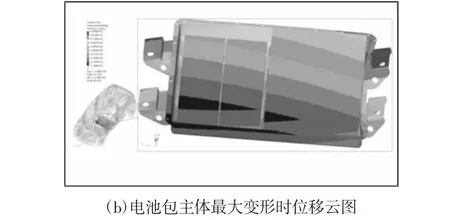
图6 50km/h 侧面碰撞整车与电池包主体最大变形情况Fig.6 The Maximum Deformation of Vehicle and Battery Package in 50km/h Side Impact
5 结论
通过CAE 分析发现某电动汽车动力电池包箱体原方案的动静态特性存在不足,出于续航里程与经济性的考虑,以厚度为设计变量,在满足动静态性能的前提下,为获得质量较小的电池包箱体,提出了一种基于Box-Behnken 响应面法与有限元仿真相结合的电池包箱体轻量化优化设计方法。(1)利用Box-Behnken 试验设计方法建立了典型路面工况下箱体最大等效应力、最大变形量和箱体结构第2 阶约束模态频率以及箱体质量对箱体各部件厚度的响应面模型,经检验可较准确反应设计变量与各响应之间的关系。(2)将响应面模型引至所建立的电池包箱体轻量化优化数学模型中进行迭代求解,获得了设计区域内最优组合(T1,T2,T3,T4,T5)=(0.7mm,1.4mm,2.1mm,1.3mm,1.1mm),相比于原结构,电池包箱体在质量与性能指标上达到了更佳的平衡状态。(3)经整车50km/h侧面碰撞工况的校核,发现车体结构承受了移动壁障的主要冲击载荷,即便最大变形时内部电池模组也未受到箱体侧壁的挤压,保证了箱体轻量化后动力电池的碰撞安全性。
