基于函数型数据时间序列建模的齿轮破损图像识别
2021-03-05孙雅娟史岳鹏冯志慧
孙雅娟,史岳鹏,冯志慧
(1.河南牧业经济学院信息工程学院(软件学院),河南 郑州 450046;2.河南牧业经济学院能源与智能工程学院,河南 郑州450046;3.河南农业大学信息与管理科学学院,河南 郑州 450002)
1 引言
齿轮是机械设备中主要的传动机械元件,被广泛应用于工业及制造业生产中[1]。齿轮破损不仅会影响自身运行状态,更是造成机器发生故障的重要原因,甚至严重危害人身安全,导致突发性事故,造成极大的经济财产损失[2]。因此,识别齿轮破损图像,对于降低设备运行风险、预防突发性事故的发生具有重要的意义和实用价值。相关领域的不同学者也对其进行了研究,并取得了一定的研究成果,文献[3]设定邻域窗口的灰度均方差积以及灰度重心方向,代表图像边缘强度及灰度变化方向,根据阈值化得到初始边缘,划分灰度变化方向,建立一维灰度矩模型,求解亚像素边缘位置,依据齿轮边缘特性结合最小二乘拟合法,实现对齿轮图像的检测效果。该方法的曝光敏感度较好,绝对定位精度较高,但该方法齿轮图像检测结果与实际不符,存在识别误差问题。文献[4]采用图像处理与识别算法,通过Halcon 软件得到标准渐开线直齿圆柱齿轮图像及基本参数,根据齿轮基本参数,获得标准渐开线轮齿轮廓,依据计算的Hausdorff 距离,判断轮齿合格标准,求得实际齿轮轮廓的Hausdorff 距离,完成轮齿轮廓缺陷检测。该方法能够有效地检测出齿轮缺陷,但该方法识别齿轮轮齿缺陷所用的时间较长,存在识别效率低的问题。
为了解决上述方法中存在的识别所用的时间长、识别结果与实际不符和识别误差大的问题,提出基于函数型数据时间序列建模的齿轮破损图像识别方法。
2 图像预处理
2.1 离散小波取低频
设(k-2i)代表的是尺度序列和二维离散图像,存在的频率子代空间都不相同,(m-2l)代表的是其余的尺度序列,将其尺度设置为零[5]。设(k,m)代表的是齿轮破损图像对应的像素值;Aj(k,m)代表的是二维齿轮破损图像。图像在频域内可以分解为高频子带成分g 和低频子带成分h,进而可以将齿轮破损图像划分为尺度为j+1 的高频图像Hj+1(m,n)和低频图像Lj+1(m,n),其表达式分别如下:

式中:Hk—齿轮破损图像被分解前存在的细节成分等纹理特性;Lj—齿轮破损图像分解前的低频分量。
小波尺度函数存在的分辨率都不相同,具有层级形式[6]。离散图像信号由于具有上述特性,能够在不同尺度中显示:

式中:αj,k—尺度系数;φj,k(x)—小波函数;dj,k—小波系数。
利用小波变换方法提取图像的低频信息,滤波器组由不同类型的滤波器构成,对图像信号进行分解处理,获得频带不同的多个子图像,图像信号在缩放变换和平移变换下被区分开,呈现出不同的特性和信号成分。
2.2 高通高斯滤波器
所提方法利用高斯高通滤波器实现图像信号的衰减操作,A(u,v)代表二维高通滤波器在理想状态下的传递函数,其表达式如下:

式中:D0—截止频率;参数D(u,v)描述的是平面原点与点(u,v)之间存在的距离,其计算公式如下:

以D0为半径画圆,将圆周频率设为零,可以通过高频信号。
高斯高通滤波进行列操作和行操作两次卷积操作,通过以上两次卷积操作可以实现去低取高的目的[7],A(u,v)传递函数的表达式如下:

随着截止频率半径D0的变小,边缘滤波效果增强。
2.3 双直方图均衡化
为了避免信息过度增强和细节信息丢失的现象,基于函数型数据时间序列建模的齿轮破损图像识别方法,将齿轮破损图像划分为两个子图,选择合适的灰度值对其进行直方图均衡。
设[m,n]代表的是齿轮破损图像对应的灰度范围;x 描述的是图像的灰度值;p(x)代表的是灰度值x 在灰度范围[m,n]内出现的频率;nk代表的是像素在灰度值中的总数,通过上述信息构建直方图px(xk):

式中:N—像素总数;T—阈值。将原始齿轮破损图像a 分为子图a1和子图a2,其对应的阈值不同,分别在最小灰度值amin与T 范围中,以及在最大灰度值amax与T+1 范围中对子图a1和a2进行均衡处理:式中:h1、h2—经过处理后的齿轮破损图像子图;n1、n2—像素在子图中对应的总数,将h1、h2子图融合并输出后进行图像信号增强处理。

2.4 图像信号增强
图像信号增强处理可以改变齿轮破损图像的质量,有效抗噪,基于函数型数据时间序列建模的齿轮破损图像识别方法,对齿轮破损图像进行信号增强处理,增强图像边缘轮廓中存在的细节成分,利于齿轮破损图像的识别。
保留傅里叶谱中存在的直流分量是图像细节增强的实质[8],增强直流分量后,再对其余成分进行增强处理,凸显纹理细节,具体过程如下:

式中:ξ—变位系数;Hh(u,v)—原始输入图像像素值。综上所述,通过小波变换提取图像的低频信息,利用高斯高通滤波器增强图像边缘滤波效果,选择合适的灰度值均衡直方图,增强图像边缘轮廓细节,有利于齿轮破损图像的识别。
3 齿轮破损图像识别
3.1 基于函数型数据分析的数据提取
为了提高齿轮破损图像识别时间,基于函数型数据时间序列建模的齿轮破损图像识别方法,通过FDA 函数化拟合具有周期性的动作捕捉数据:
(1)设[ax,ay,az,ωx,ωy,ωz]代表的是通过传感器采集的6 维信号,其中ax、ay、az代表的是X 轴、Y 轴和Z 轴对应的加速度;ωx、ωy、ωz分别代表的是X 轴、Y 轴和Z 轴对应的角速度信息。
(2)在每个维度中对6 维信号对应的时间序列y=(y1,y2,…,yn)进行建模:

式中:εi—噪声;x(ti)—在t 处观测数据序列函数x(t)对应的取值。通过基函数展开方法求取x(ti)的值:

式中:ck—基函数的线性组合;(ti)—离散数据。
设C 代表的是稀疏向量,确定基函数后得到其表达式:

齿轮破损数据属于周期型的观测数据[9],其基函数可以选用傅里叶级数:
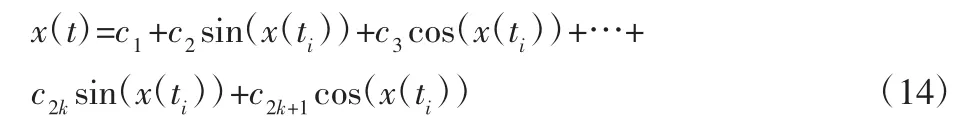
(3)均匀采集拟合函数,提取序列,其长度与单周期样本点相似:

式中:DL—周期性时序数据。通过上述步骤拟合具有周期性的动作捕捉数据。
3.2 时间序列建模
HMM 描述的是马尔科夫链中存在的简单概率模型,HMM的基本思想是通过双重随机过程描述观测值和随机过程之间存在的关系以及马尔科夫链,HMM 的表达式如下:

式中:B—观测值概率矩阵;Z—马尔可夫链在模型中的状态数目;A—状态转移矩阵;π—状态概率分布矢量;M—观测值对应的数目。
采集数据经过函数化处理后即为观察层中的输出序列:

显示层中存在的节点均是每帧的6 维向量。通过排列组合获得运动状态集合U:

其中,u1,u2,…,u9均代表的是不同行为。
设λ1,λ2,…,λ9代表的是不同行为对应的模型,设将观测值对应的数目M 设置为9,采用K-means 聚类算法获取马尔可夫链在模型中的状态数目Z,并设置状态转移矩阵A 和状态概率分布矢量π,选取均匀分布的输出概率矩阵bij,其表达式如下:

4 实验结果与分析
为了验证基于函数型数据时间序列建模的齿轮破损图像识别方法的整体有效性,实验在英特尔酷睿i5 2.5 GHz CPU、4GB RAM 平台中进行测试,通过MATLAB R2013a 实现。选取齿数为100,模数为2.5,螺旋角为9°,变位系数为0 的中小模数齿轮进行测试,分别采用所提方法、文献[3]方法和文献[4]方法进行对比,对比三种方法识别齿轮破损图像所用的时间,测试结果,如图1 所示。

图1 三种方法的识别时间Fig.1 Identification Time of Three Methods
根据图1 中的数据可知,随着齿轮破损图像的增大,所提方法的识别时间均低于文献[3]方法和文献[4]方法的识别时间,由此可知,所提方法的齿轮破损图像识别时间较短,识别效率较高。因为所提方法通过FDA 对具有周期性的动作捕捉数据进行了函数化,利用函数型数据分析方法,拟合动作捕捉数据,能够用多个周期的时序数据代替动作捕捉数据,从而有效缩短识别齿轮破损图像所用的时间,提高齿轮破损图像的识别效率。
为了验证所提方法的识别误差,分别采用所提方法、文献[3]方法和文献[4]方法进行对比,对比不同方法齿轮破损图像识别结果与原始齿轮破损图像,如图2 所示。图2 中采用方框表示原始齿轮破损位置。

图2 三种方法的齿轮破损图像识别误差Fig.2 Gear Damage Image Recognition Error of Three Methods
根据图2 中的齿轮破损图像识别结果对比可知,采用所提方法的齿轮破损图像识别结果与原始齿轮破损位置相符,而采用文献[3]方法的齿轮破损图像识别结果未全部识别出齿轮破损处,采用文献[4]方法的齿轮破损图像识别结果识别出齿轮未破损处,由此可知,采用所提方法得到的齿轮破损图像识别结果与实际相符,识别误差较小。因为所提方法将齿轮破损图像划分为两个子图,并选择合适的灰度值对其进行直方图均衡,利于齿轮破损图像的识别,有效减小齿轮破损图像识别误差。在此基础上进一步验证齿轮破损图像的识别效果,实验加入σ=0.002 的高斯噪声齿轮破损图像,分别采用所提方法、文献[3]方法和文献[4]方法进行对比,对比不同方法的齿轮破损图像识别效果,如图3 所示。

图3 三种方法的识别效果Fig.3 Recognition Effect of Three Methods
由图3 可知,采用文献[3]方法识别的齿轮破损图像,图像边界模糊,缺少边缘轮廓细节信息,采用文献[4]方法识别的齿轮破损图像,图像边界清晰,边缘轮廓细节信息完整,但边缘轮廓中细节信息繁多,导致识别结果存在误差,而采用所提方法识别的齿轮破损图像,图像边界清晰,边缘轮廓细节信息完整,由此可知,所提方法的齿轮破损图像识别效果较好。因为所提方法对齿轮破损图像进行信号增强处理,能够有效抗噪,提高齿轮破损图像质量,增强图像边缘轮廓中存在的细节成分,从而提高齿轮破损图像的识别效果。
5 结语
目前齿轮破损图像识别方法识别齿轮破损图像时,存在识别效率低、识别误差大、识别效果差的问题。提出了基于函数型数据时间序列建模的齿轮破损图像识别方法,采用小波变换及高斯高通滤波器提取图像高低频信息,选择灰度值均衡直方图并进行图像增强处理。根据函数型数据分析拟合动作捕捉数据,构建周期时间序列获得隐马尔可夫模型,通过最大似然估计函数,计算测试模型与样本之间的匹配度,实现齿轮破损图像的识别。该方法可以在较短的时间内准确地完成齿轮破损图像的识别,有效降低了识别误差,提高了识别效果,为图像识别技术的发展奠定了基础。
