BP+RNN 变速积分PID 算法的汽车底盘测功机控制系统
2021-03-05陈宇轩
周 洲,陈宇轩,程 鑫
(长安大学信息工程学院,陕西 西安 710064)
1 引言
汽车底盘测功机是一种检测汽车动力性、输出功率和尾气排放等性能的机械设备,它通过PID 控制影响飞轮惯性的转动惯量,以此对汽车驾驶时的转动惯量进行仿真,从而对汽车的运行状况进行动态检测[1-2]。PID 算法的系数整定是一个复杂的问题,而当其应用于汽车底盘测功机这种复杂的时变非线性、具有强惯性的大型设备时,系数的整定会更加困难[3-4]。
文献[5]在PID 算法参数整定过程中结合模糊推理机制,首先根据输入误差确定模糊论域与隶属度函数,接着采用Mamdani算法作为模糊推理的方法,最后确定出一个符合当前情况的模糊矩阵表,根据该表整定对应的PID 参数。这种方法的特点是能够对PID 算法参数进行实时矫正,提高精确度。但由于需要预先通过一系列流程建立模糊矩阵表,且该表不具备普遍性,因此费时费力,不适用于需要经常改变条件的实际应用中。文献[6]利用神经网络具有自主学习的功能,且善于处理多输入、非线性对象的特点,成功将BP 神经网络与增量式PID 算法相结合,并引入相应的工业运用当中。通过实验证明了BP 神经网络与PID 算法的结合使控制响应速度变快,是实现提高PID 算法效果的有效方法。文献[7]进一步将PID 算法中的神经网络改为RBF 径向基神经网络,凭借径向基神经网络能够降低网络复杂度,减少输出层部分神经元与网络权值的数量,使得网络收敛速度变快、参数自整定能力变强。根据实验结果,径向基神经网络PID 控制算法实际效果良好,且具有很强的鲁棒性及抗干扰能力。相关一系列研究均说明了在汽车底盘测功机上使用神经网络PID 控制方法的可行性。文献[8]在汽车底盘测功机PID 控制过程中使用了基于RBF 径向基函数神经网络的策略。首先通过分析汽车底盘测功机实际运行情况建立了加载模型,接着根据底盘测功机的加载力输出特性设计了结合RBF 径向基函数神经网络的工作模型,最后在神经网络的训练基础上进行PID 控制。这种方法的特点是底盘测功机的输出力上升过程稳定且快速,并且不需要费时费力的进行PID参数整定工作,但算法在控制过程中的初始阶段依然存在明显的超调情况。由于底盘测功机涡流机的运作具有一个加载时间,导致汽车底盘测功机的响应延迟。因此采用传统增量式PID 控制的过程中积分项会不断累积,在启动、停止或大幅度更改控制目标时,积分项输出通常造成汽车底盘测功机出现大额超调现象。文献[9-11]均提出在工业应用当中使用变速积分PID 算法控制,该算法能够有效的使PID 控制中的积分项效果在系统偏差较大时减小或取消,而在系统偏差较小时则相对增大。通过变化的积分项参数来消除PID 在一些情况下对控制稳定性的负面影响,从而在不对系统造成干扰的情况下减小静态误差与超调。
在此背景下,对神经网络PID 思想与变速积分PID 方法分别进行研究,将二者进行了融合改良,设计出一种BP+RNN 变速积分PID 算法控制系统,将其应用于汽车底盘测功机,实现快速的整定PID 参数与减少超调、增加控制性能。
2 BP+RNN 变速积分PID 控制系统
2.1 系统设计
BP+RNN 变速积分PID 算法控制系统是把BP 神经网络与RNN 网络组合应用到汽车底盘测功机的控制当中,并搭配能够消除控制超调的变速积分PID 算法,融合这些方法的优点,从而对传统增量式PID 算法在控制汽车底盘测功机时存在的一系列问题进行优化。BP+RNN 变速积分PID 算法控制系统能够大致分为两个部分,如图1 所示。

图1 BP+RNN 变速积分PID 控制流程图Fig.1 Flow Chart of BP+RNN Variable Speed Integral PID Control
第一个部分是变速积分PID 控制环节。从神经网络输出端实时接受三个PID 参数KP、KD与KI,输入变速积分PID 算法中进行计算,得到当前汽车底盘测功机所需控制量u(k),将该控制量传送给汽车底盘测功机的滚筒进行控制。通过内置计数器每间隔5ms 采样一次汽车底盘测功机在该组PID 参数控制下的运行状态r(k),将该运行状态传送到BP 与RNN 网络进行自学习调整。
第二个部分是BP 神经网络与RNN 的自学习。首先设置一组初始PID 比例项参数KP、微分项参数KD与积分项参数KI,在此条件下控制运行汽车底盘测功机,每间隔5ms 采样一次汽车底盘测功机在该组参数控制下的运行状态r(k)。将其与目标值y(k)带入均方误差法损失函数,得到神经网络损失值,利用损失值反向传递训练BP 神经网络和RNN 网络,优化两个网络的权值参数ω。同时将该运行状态r(k)与目标值y(k)相减得到当前时刻误差。将得到的本次误差作为RNN 网络模型的输入,并把本次误差e(k)、上次误差e(k-1)及上上次误差e(k-2)作为BP 神经网络模型的输入,通过神经网络计算得出一组PID 参数。将该组参数作为新的PID 参数重复控制运行汽车底盘测功机。最终可以从BP 神经网络模型中得到实际运行状态下汽车底盘测功机PID控制器中的比例项参数KP和微分项参数KD,并从RNN 网络模型中输出实时符合当前误差状态的时变积分项参数KI。随着控制的进行,变化的积分项参数也将实时更新,不断改变控制量的大小,使底盘测功机的运行效果满足工业要求。
2.2 变速积分PID 算法
传统的增量式PID 控制策略在处理车辆底盘测功机这种具有较高延迟性的场景时,积分项容易在控制调节工作中超额累加,从而导致整个系统的控制出现大额超调。变速积分PID 是一种改良的PID 算法,它能够控制积分项的实时系数大小,从而与实际运行情况相匹配[12]。使该算法在汽车底盘测功机误差较大时积分项减小或归零,相反在汽车底盘测功机误差较小时积分项则增大,从而达到大幅度减小PID 控制超调的效果。变速积分的PID 算法的表达式为:
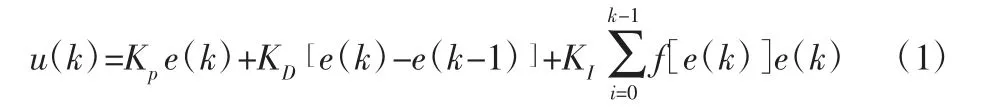
式中:e(k)—误差,是汽车底盘测功机中滚筒的控制目标状态y(k)减去实际运行状态r(k),等式相加的第三项即为算法积分项。可以看到变速积分PID 为积分项参数KI增添了一个矫正函数f[e(k)],此函数通常是关于误差的,原则上当误差增大时f[e(k)]减小,反之则增大。
变速积分PID 算法的优势在于根据实际运行的误差大小自动调节积分项的控制参数,提高整个系统的适应性,能够减小底盘测功机在起步、急停等状态变化较大的非稳定运行状态下,目标积分项阶跃输入对实际控制的影响,提高系统的控制稳定性。
2.3 BP 神经网络自学习

图2 BP 神经网络结构图Fig.2 Structure of BP Neural Network
对实验所用的汽车底盘测功机实际控制效果进行分析,建立三层结构BP 神经网络模型并进行初始化,该模型包含3 个输入层神经元,3 个隐含层神经元和2 个输出层神经元。其结构图,如图2 所示。
设置初始PID 比例、微分项参数,实时采样当前参数运行情况,计算得到的汽车底盘测功机实时控制过程误差,将当前误差e(k)、上次误差e(k-1)、上上次e(k-2)误差作为训练BP 神经网络输入层节点的输入。即网络输入层输入为:

正向计算BP 神经网络,得到隐藏层神经元的输入与输出为:

式中:ω(2)—隐藏层权重矩阵,f[·]=tanh(x)。标记(1)、(2)依次对应输入层、隐藏层。进一步正向计算得到BP 神经网络输出层神经元的输入与输出为:

2.4 RNN 网络自学习

图3 RNN 网络结构图Fig.3 Structure of RNN Network
对实验所用的汽车底盘测功机实际控制效果进行分析,建立三层结构RNN 神经网络模型并进行初始化,该模型包含1 个输入层神经元,1 个隐含层神经元和1 个输出层神经元。其结构图,如图3 所示。
采样得到被控汽车底盘测功机滚筒的实时加载扭力,利用该扭力与目标加载扭力相减计算,得到系统实时运行误差,将该误差e(k)作为RNN 网络自学习时输入层节点的输入。即网络输入层输入为:

正向计算RNN 网络,得到隐藏层神经元的输入与输出为:

式中:ω(2)—隐藏层权重矩阵;υ(2)—隐藏层上一时刻对这一时刻影响的权重矩阵,f[·]=tanh(x)。标记(1)、(2)依次对应输入层、隐藏层。进一步带入式(4)正向计算,得到RNN 网络输出层神经元的输入与输出。其中,O(3)(k)=KI即所求的时变积分项参数。
将得到的积分项参数KI与BP 神经网络计算出的比例项参数KP和微分项参数KD带入式(1)变速积分PID 算法中,计算得到PID 控制器当前时刻控制量,通过式(5)采用均方误差(Mean squarederror)法计算当前时刻神经网络损失。选择学习率η=0.05,动量系数α=0.05,按照梯度下降法对输出层的权值ω(3)进行优化,调整算式为式(6)。接着按照梯度下降法对隐藏层的权值ω(2)进行优化,调整算式为:

同理按照梯度下降法修正隐藏层上一次值对这一次值影响的权重矩阵υ(2),调整算式为:

其中,f′[·]=[1-f2(x)]/2。
3 算法实验研究
3.1 仿真实验结果
MATLAB 是一款系统模型库的功能十分丰富的仿真平台,因此使用MATLAB 建立仿真系统,使用模拟的数据进行仿真实验,并观察仿真结果,证实算法可行性,充分提高了工作效率。选择相同的初始条件针对底盘测功机的恒力运行状态进行仿真控制,分别使用传统增量式PID 算法、一般神经网络PID 算法以及文中提出的BP+RNN 变速积分PID 算法控制系统建立系统仿真模型。根据结果进行对比分析。
首先测试传统增量式PID 算法,通过初步测试选择KP=0.75、KD=0.5、KI=0.15 作为PID 算法的三个参数值,同时将这三组参数作为一般神经网络PID 算法以及BP~RNN 变速积分PID 控制算法的参数初值。仿真系统采用阶跃信号作为其输入,传统增量式PID 算法仿真结果,如图4(a)所示。从图中可以得到,使用传统增量式PID 算法控制,系统需要经过大约80ms 趋于稳定,且控制时出现较大超调与震荡,效果不理想。

图4 算法仿真结果Fig.4 Algorithm Simulation Results
然后测试一般神经网络PID 算法的仿真结果,如图4(b)所示。从图中可以得到,系统只需约50ms 便可趋于稳定。相比于传统增量式PID 算法,控制时间大幅缩短,且未出现大幅震荡现象,控制效果大幅提高,但在控制初始阶段依然出现较大超调。
最后测试文中提出的BP+RNN 变速积分PID 算法控制系统的仿真结果,如图4(c)所示。从图中可得系统约花费50ms 便趋于稳定,且相比于一般神经网络PID 算法,控制初始阶段的超调基本消除,系统准确度大幅提升。由仿真实验结果得出该算法实施的可行性。
3.2 实际应用结果
该次实验利用BP+RNN 变速积分PID 算法控制系统对某型号汽车地盘测功机进行实际应用测试,实验场所位于长安某实验场进行,实验工作场地,如图5 所示。

图5 实验工作场地Fig.5 Experimental Work Site
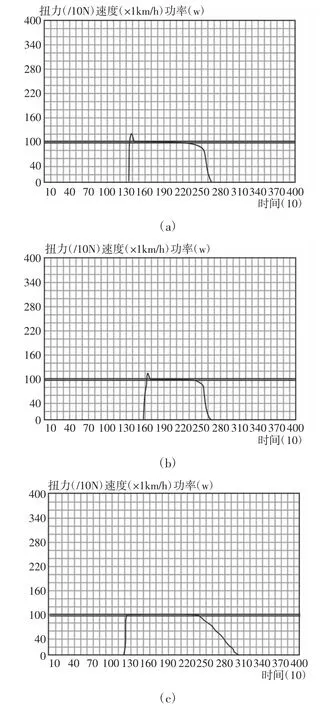
图6 实际应用控制效果图Fig.6 Practical Application Mode Diagram
根据国家质量监督检验检疫总局2018 年发布的底盘测功机使用标准,底盘测功机运行状态的工业要求误差不大于2.0%,加载响应需在时间300ms 内达到90%。经过基本标定与测试后选择当前控制条件下初始的PID 参数KP=0.633、KD=2.315、KI=0.347。将参数带入传统增量式PID 算法进行汽车底盘测功机的控制,其控制效果,如图6(a)所示。从图中可以得到,控制花费约100ms 趋于稳定,但该使用该算法花费了大量时间用于整定PID参数,且控制初始阶段出现大量超调;接着将初始化的参数带入一般神经网络PID 算法进行汽车底盘测功机的控制,其控制效果,如图6(b)所示。从图中可以得到控制花费约100ms 趋于稳定,仅出现轻微超调;最后将参数带入这里的BP~RNN 变速积分PID 控制算法进行汽车底盘测功机的控制,其控制效果,如图6(c)所示。控制花费约60ms 趋于稳定,且没有出现超调。从实际实验结果中可以看出此BP~RNN 变速积分PID 控制算法应用在汽车底盘测功机时的优越性与稳定性。
4 结论
这里介绍了一种BP+RNN 变速积分PID 算法控制系统在汽车底盘测功机应用的原理与效果。利用变速积分PID 算法在系统偏差较大时积分项减小或取消,而在系统偏差较小时增大的特点,在不对系统造成干扰的情况下减小静态误差与超调,解决了在处理高度非线性、时滞性、运行机器的条件复杂的汽车底盘测功机系统时,增量式PID 容易出现积分饱和的问题。在参数的整定方面,采用BP 神经网络整定变速积分PID 算法的比例项、微分项参数,做到参数的快速自适应调节。同时利用RNN 网络具有时序性因素的能力、能够根据历史数据推断结果的特点,整定变速积分PID 算法的时变积分项参数。
经过重复多组不同条件下的实际运行,证明该系统兼顾了高效与准确的优点,拥有出色的实际运行结果。相比与普通汽车底盘测功机控制效果,该系统能够准确快速的整定出PID 系数,并且能够有效避免控制的过程中积分项的不断累积,可以消除在启动、停止或大幅度更改控制目标时,积分项输出造成汽车底盘测功机出现大额超调现象,同时避免测功机改变目标环境时产生的震荡与静态误差。该BP+RNN 变速积分PID 算法控制系统的未来方向是进一步丰富完善设计,从而能够得到更准确的控制效果,并且可以运用到更多场合。
