斗提式散粮卸船机提升装置振动特性研究

李永祥，靳航嘉，王明旭，李 阳

（河南工业大学机电工程学院，河南 郑州 450001）

1 引言

我国人口数量众多，人民对高品质粮食需求量越来越大。我国粮食已经不能自给自足，需要大量进口粮食来弥补供需缺口。同时大量农村劳动力向城市转移，未来粮食供需缺口有不断扩大趋。进口粮主要以海运为主，卸船机在港口散粮接卸发挥主要作用。目前港口用于散粮的卸船机可分为间歇式和连续式两种，类型较多，各有优劣[1]。连续式卸船机的类型与物料垂直提升的方式关联密切。在物料的垂直提升方式中，斗提机在提升同样的高度时，输送路程最短，效率高、无扬尘等诸多优点。因此斗提式散粮卸船就具有更大优势。

卸船机工作时，由于振动源以及设备本身结构布局，再加上海边风浪等因素的作用，容易使提升部分发生振动，影响粮食提升效率，缩短设备的使用寿命。因此对这种新型的斗提式散粮卸船机的动力学特性进行研究十分必要。

2 斗提式散粮卸船机工作原理

斗提式散粮卸船机示意图[2]，如图1 所示。斗提机在新型卸船机中的工作状态有别于传统斗提机，在工作时，需要根据船舱内粮面的高度，调整俯仰角度，因此整个提升装置上部与桁架铰链接，下部无固定链接，斗提机处于悬臂状态。会因下部螺旋喂料和海边风浪等因素而发生振动，悬臂梁的主要振动形式也是弯曲振动。因此，针对卸船机提升装置的弯曲振动特性进行研究非常重要。

图1 斗提式散粮卸船机示意图Fig.1 Schematic Diagram of Bucket Elevator Type Bulk Grain Ship Unloader

3 斗提式卸船机提升段弯曲刚度分析

斗提式卸船机提升段截面为中心对称图形，如图2 所示。

图2 提升段截面简图Fig.2 Sketch of the Cross Section of the Lifting Section

设宽为B，长为L，每块侧板厚度为b，将截面整体按从上之下，从左至右划分为I，II，III，IV，V，VI，6 个矩形部分。以提升段截面形心为原点建立坐标系xCy，y1和z1为惯性主轴

矩形I：

θ 值可以确定主惯性轴y1和z1的位置，继而可求得截面对于主惯性轴y1和z1的惯性矩：

如果驱动弯矩与主惯性轴z1同向，弯曲刚度kg为：

式中：E—提升段材料的弹性模量；H—提升段高度。

斗提机外壳的主要材料是结构钢，弹性模量E=200GPa，

本设计的斗提机截面尺寸参数，如表1 所示。

表1 提升段截面尺寸参数Tab.1 Dimensions of the Lifting Section

将表1 中数据带入式（3），可算得：Iy=3.1890×10-2m4；Iz=6.0129×10-2m4带入式（4）可得：Iy1=6.0129×10-2m4；Iz1=3.1890×10-2m4带入式（6）可得：kg=4.0199×108N/m

4 提升装置弯曲振动理论

4.1 提升段动力学方程

对提升装置弯曲振动进行研究，将斗提机简化为竖直悬臂梁，将喂料装置简化为端部质量块，简化后模型，如图3 所示。竖直高度为H，E 为提升段材料的弹性模量，I 为提升段横截面的对于形心轴的二次截面距，竖直悬臂梁单位长度的质量为m，质量块的质量为m0。图中：Fs和F右—微元左右端面所受的剪力；M 和M右—微元左右

图3 提升段微元动态平衡示意图Fig.3 Schematic Diagram of Dynamic Balance of Lifting Segment Micro-Element

端面弯矩，微元的惯性力为F惯性力，用y（x，t）表示距原点x

处的截面在t 时刻的横向位移，则有：

可建立动力平衡方程：右截面力矩平衡方程：忽略高阶小量，由弯矩与挠度的关系，得到动力学方程：

梁的主振动[3]可假设为：

将式（13）带入式（12）中，得：

由高等数学可知，上式通解为：

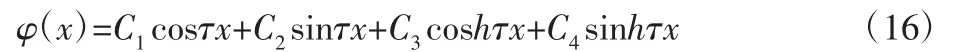
C1、C2、C3、C4可以通过竖直悬臂梁的边界条件来确定。

4.2 边界条件

悬臂梁边界条件由端部的约束条件来确定，卸船机提装置的边界条件为：固定约束的端面的挠度曲率和位移为0。

确定提升装置自由端边界条件时，下部自由端有质量块连接，可以对质量块进行受力分析，如图4 所示。

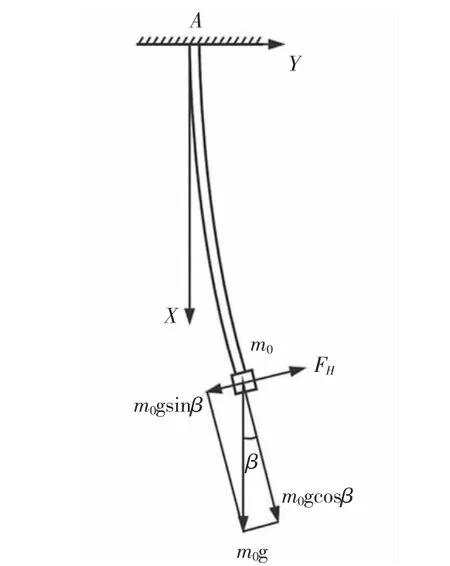
图4 质量块受力分析Fig.4 Force Analysis of Mass

图中：FH—竖直悬臂梁端面对质量块的力，将质量块的重力m0g沿质量块运动方向和垂直运动方向分解，分别为m0gsinβ 和m0gcosβ，力的作用点为质量块的质心。

质量块的在运动方向上的动力平衡方程为：

上文中已经假设提升装置在竖直平面内做微幅振动，所以β 角非常小，m0gsinβ 趋近于0，可忽略不计，可得：

4.3 提升装置固有频率和振型

所以，可以得出悬臂梁在自由端的边界条件为：弯矩为零，剪切力与质量块惯性力平衡，故：

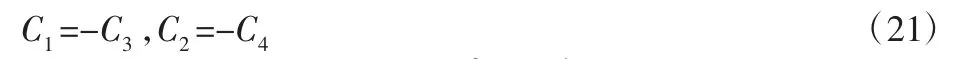
由固定端边界条件，可得：由自由端的边界条件，并令ψ2=EIτ4，可得：

由C1、C2有非零解得，得出频率方程：

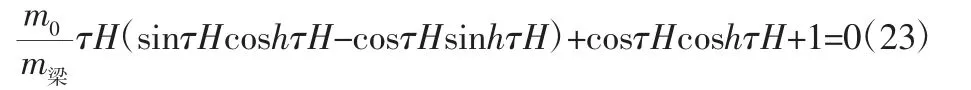
式中：m0/m梁—自由端质量块与竖直悬臂梁质量之比，对于本次设计的提升装置，m0/m梁=0.3463306。

利用MATLAB 对式（23）进行求解，令x=τH，将式（23）分为M=-（m0/m梁）x（sinxcoshx-cosxsinhx）和N=cosxcoshx+1 两个方程，用x=x+0.0001 依次递增0.0001 的方式循环带入两个方程中，当|N-M|≤0.001 时输出x 值。程序如下：

求得前四阶值分别为：x1=1.6925；x2=3.3624；x3=12.1251；x4=17.7802，可以得出系统前四阶固有频率：

由上文算得截面矩，再由m=m梁/H，H=19m，m梁=24782.45kg，算得前四阶固有频率：

5 仿真验证及误差来源分析

为了验证上述理论结果的可靠性，使用ANSYS 对提升装置悬臂梁结构进行模态分析，同样得出此结构弯曲振动的固有频率和振型，并与理论结果进行对比分析[4-5]，步骤包括：首建立了提升装置三维模型，将喂料装置视为端部质量块，皮带、畚斗视为小质量块，并忽略螺栓、螺母。设置材料属性，设置约束，并求解。结果如图5、表2 所示。

图5 提升装置前四阶模态振型Fig.5 The First Four Modes of the Lifting Device

表2 理论值与仿真结果对比Tab.2 Comparison of Theoretical and Simulated Values

从表2 可以看出装置固有频率的理论计算值与仿真结果值误差在5%以下，误差主要来源有以下几点：

（1）确定自由端边界条件时，忽略了微幅振动时质量块自重的影响。

（2）整个提升段结构并非是均匀一体的，而是由多段结构通过法兰连接在一起。导致理论模型和仿真模型的偏差。

（3）理论计算时以提升高度作为竖直梁的高度，仿真分析时要略大于此值，导致理论值偏大。

（4）MATLAB 求解时，精确度为0.001，结果存在误差。

6 结论

卸船机提升装置的主要振动形式为弯曲振动。从理论上计算了提升段等效弯曲刚度。利用微元法建立了提升段弯曲振动的动力学方程，通过对端部质量块的力学分析，确定了弯曲振动的边界条件，得出了弯曲振动的频率方程。利用MATLAB 求解频率方程，得出了提升装置弯曲振动的前四阶固有频率，分别为：0.5971Hz、1.1863Hz、4.2777Hz 和6.2729Hz。使用ANSYS 对提升装置进行模态仿真，得到了前四阶固有频率和振型。从理论结果和仿真结果对比来看，误差值在5%以下，理论结果具有可靠性。