两光子三自由度的杂化纠缠W态

2021-03-05李晓峰金锦双杨垂平

杭州师范大学学报(自然科学版) 2021年1期

李晓峰，金锦双，杨垂平

(杭州师范大学理学院，浙江杭州 311121)

量子纠缠[1]是量子信息通信过程中最重要的资源之一,在量子信息领域是一种不可缺少的资源[2].它将两个或多个看似独立的粒子或者量子比特不可分割地联系在一起,是量子系统中多粒子的非定域关联.其最简单的形式是所谓的二体纠缠,常见的为Bell态[3].经过近20年的理论和实验研究,科学家对二体纠缠态的结构和特性有了清晰的认识.但随着对量子纠缠更深入的研究,科学家普遍认为,随着共享纠缠各方数量的增加,纠缠的结构和动力学变得更加复杂.常见的多体纠缠态有GHZ态和W态等,它们不是二体纠缠的简单推广,一个重要特性就是它们不能通过随机局部运算和经典通信(Slocc)相互转换[4].GHZ态是最大纠缠态,可以被用来演示违背Bell不等式[5]、隐形传态[6]以及超密集编码[7]等.而W态是非最大纠缠态,它已被认为是实现一系列量子协议的较有希望的候选者[8-9].

多体的量子纠缠往往是很脆弱的,容易丢失信息,尤其像GHZ态这样的最大纠缠态[4].而多粒子纠缠的W态不同于一般的纠缠,即使某一粒子丢失信息,剩余粒子仍可能存在纠缠关联[10].因此非最大纠缠的多体纠缠态——W态在量子计算和量子信息科学领域引起了相当大的关注.近十几年来,在线性光学领域中,科学家通过光学器件制备出各种不同量子比特和自由度纠缠的W态.2004年,德国Eibl等用两个纠缠光子对(EPR光子)制备出基于偏振纠缠的三量子比特W态[9].2009年,日本的Tashima 团队用更优的方法制备出两类等概率的三量子比特的W态[11]; 2010年,该小组对制备方法再次改进,提高了制备三光子W态的保真度,并制备出四光子W态[12].上述方案制备的W态都是基于单一的光子偏振自由度上.随着深入研究,科学家发现在实际的量子信息处理过程中,单一自由度的量子纠缠会受量子通信中噪声和退相干等因素的影响,使得某些情况下,单一自由度的纠缠不能完全满足实际量子信息的处理需求.因此，随之向着制备多自由度纠缠态的方向研究.2010年,潘建伟团队实验证明了超纠缠十量子比特薛定谔猫态[13], 报道5个光子中每个光子是偏振和路径自由度的超纠缠.2011年,陈理想团队理论验证了基于偏振、路径和轨道角动量(orbital angular momentum,简记为OAM)三自由度的GHZ态[14].2015年,潘建伟团队再次通过实验实现单光子的多自由度的量子隐形传态[15].对于多自由度纠缠的W态,范榕华团队于2015年提出三光子多自由度纠缠W态的方案[16].相对于单自由度的情况,多自由度纠缠的量子态使量子通信具有更大的信道容量和更有效的处理量子信息,且能与多种量子网络兼容.本文将设计出制备两光子三自由度杂化纠缠W 态的方案,实现利用少量资源制备多自由度杂化的纠缠W态,并且将大大提高制备效率.

本文首先制备出两光子两自由度(路径-偏振-偏振)杂化纠缠的W态.其中A光子经特殊分束器(polarization-dependent beamsplitter, 简记为PDBS)和HWP等光学器件组成的干涉仪形成偏振和路径编码的超纠缠态.然后将B光子的偏振自由度转换成OAM自由度,得到两光子三自由度杂化纠缠的W态.最后提出如何间接探测和验证所制备的杂化纠缠W态的实验理论方案,以此论证能成功制备两光子三自由度杂化纠缠的W态.

1 两光子两自由度杂化W态制备

本文方案主要涉及线性光学器件,其中最为关键的器件是PDBS. PDBS对H(水平偏振)光和V(垂直偏振)光的作用如图1所示,用公式表示分别为

(1)

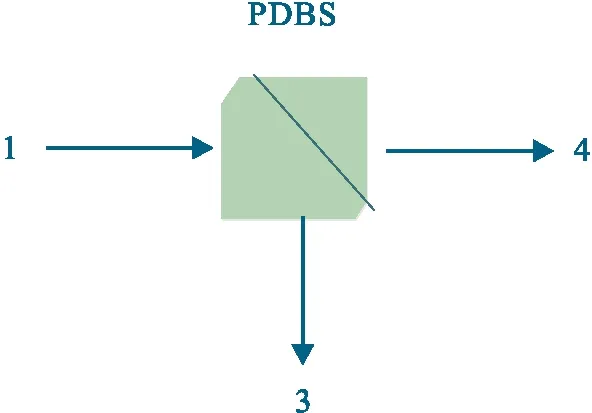
图1 光子态经PDBS的演化Fig.1 The evolution of photonic states through PDBS

本文将要制备两光子三自由度杂化纠缠的三量子比特W态,其光路图如图2所示.具体制备过程如下：先利用泵浦激光束打在非线性晶体β相偏硼酸钡(BBO)上,再利用BBO的自发参量下转换过程产生偏振纠缠光子(AB)对：

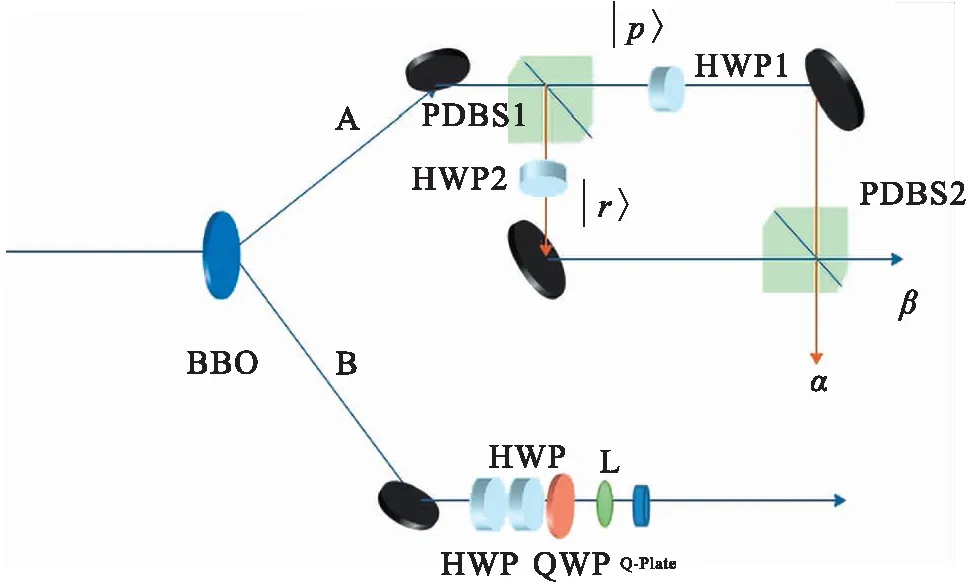
图2 OAM、偏振和路径纠缠W态的方案Fig.2 W state scheme of OAM, polarized and path entangled

其中, |H〉与|V〉分别表示光子的水平偏振态与垂直偏振态.A光子经过由PDBS组成的干涉仪进行态演化,而B光子则另外单独操作.

首先考虑A光子,经PDBS1后,根据式(1)、(2)的态演化成

(3)

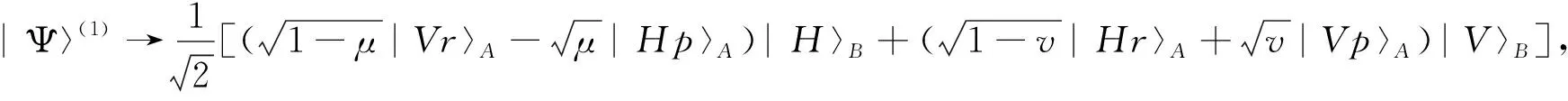
最后,两路径光子态再经PDBS2整合,式(4)中的态最终演化为

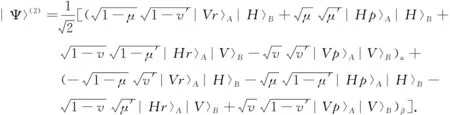
其中,μ′(v′)是H(V)光在PDBS2的透射系数.上述的|Ψ〉(2)中A光子态是被PDBS2分为α、β两个部分上.根据式(5), 就能得到α部分上的态为

β部分上的态为

此处选择v′为0时,式(6)和(7)的态分别变成如下：

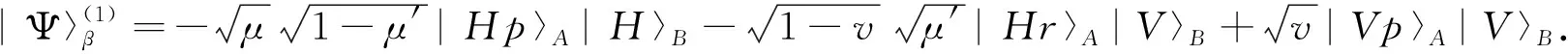
这样式(5)就成为两个三项态叠加的态

本文的目的是制备标准的三量子比特W态,式(8)和(9)中系数需要满足关系式

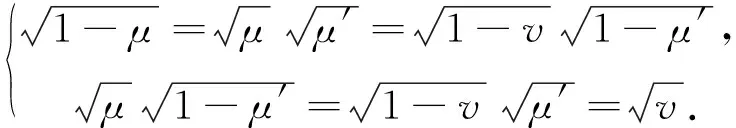
那么推得所用到的PDBS参数：μ为2/3,v为1/3,μ′为1/2.此时,式(8)和(9)的态表示为：

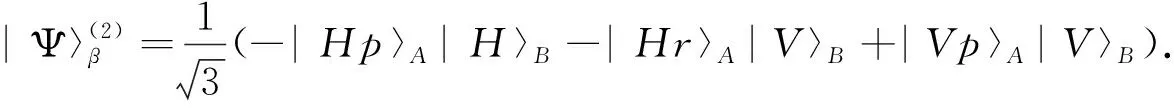
将|H〉和|r〉看作|0〉,|V〉和|p〉看作|1〉, 那么式(11)就是两光子三量子比特纠缠的W态

式(12)是另一个三量子比特的三项态

最后输出端的末态就可以是两光子三量子比特纠缠的W态和三项态的叠加,即可以将式(5)写成

其中，α部分是三量子比特W态,β部分是一个三项态.值得注意的是：这部分只对A光子进行了推演, B光子未做处理,因此|Ψ〉(2)中的α部分还只是一个两光子两自由度纠缠的W态.

2 两光子三自由度杂化W态制备

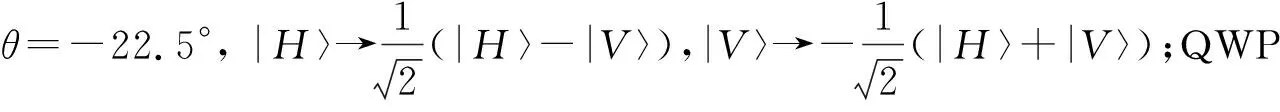
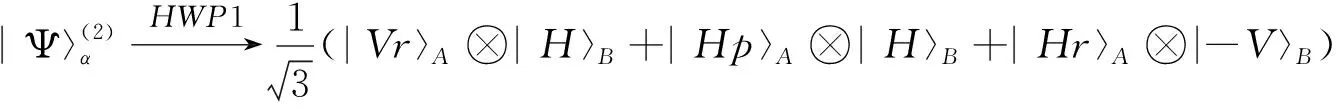
其中, |L〉和|R〉是圆偏振态,分别表示左旋偏振态和右旋偏振态.

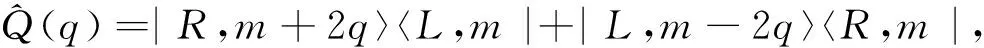
其中：|m〉为OAM的本征态；q是常数,由Q-plate本身性质所决定.式(14)和(15)中, B光子态还不具有OAM自由度,所以QB(q)中的m为0.B光子经透镜聚焦进入Q-plate后,式(14)和(15)量子态演化为：

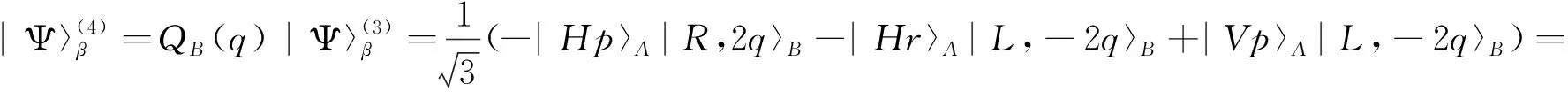
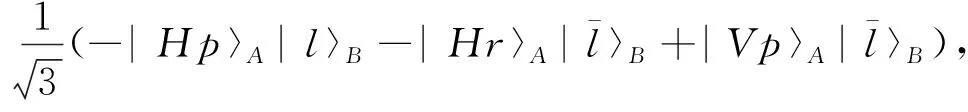
3 W态的检测

图3 A、B光子态的探测Fig.3 Detection of photons A and B

3.1 密度矩阵ρBE的获取

探测B光子的OAM(B)和A光子的偏振(E)量子比特组成的量子态,ρBE.先确定A光子的路径态,然后3个探测器进行光子符合探测.若路径态为|p〉, 探测到B、E二量子比特态的情况如图4a所示;若路径态为|r〉, 探测到B、E二量子比特态的情况如图4b所示.

a.路径态为|p〉

3.2 密度矩阵ρBF的获取

同理,探测B光子的OAM(B)和A光子的路径(F)量子比特组成的量子态,ρBF.先确定A光子的偏振态,然后3个探测器进行光子符合探测.若偏振态为|H〉, 探测到B、F二量子比特态的情况如图5a所示; 若偏振态为|V〉, 探测到B、F二量子比特态的情况如图5b所示.

a.偏振态为|H〉

3.3 密度矩阵ρBEF

由于纯三量子比特态可由其两个二量子比特的态唯一决定[23-24],根据该理论,用探测到的ρBE和ρBF可以得到三自由度纠缠态的密度矩阵ρBEF，

而ρBEF与标准的三量子比特纠缠的W态密度矩阵ρW=|W〉〈W|相同,这样就可以间接地验证所制备的态就是W态.

4 W态的抗干扰性

对于本文制备的W态,若在自由空间、光纤传输以及态演化的过程中,即使任意一个自由度所对应的量子比特丢失了,该量子态仍有可能存在着纠缠关联.假设代表OAM自由度的量子比特B丢失了,这相当于对量子态密度矩阵关于量子比特B求迹：

根据式(18)可知,若光子在传输的过程中丢失了量子比特B, 光子剩下的量子态仍有2/3的概率是纠缠的.将式(18)用矩阵形式表示为

那么通过计算,丢失任意一个比特后的量子态保真度为5/9.

5 展望

本文利用以上光路图，不仅制备了两光子三自由度杂化纠缠的W态，还可以将纠缠光子源换成单光子源,用SLM给初态光子编码上OAM和偏振两个自由度，然后将编码的态输入上文A光子的演化光路,制备出单光子三自由度杂化纠缠的W态.如果简单调整光路和PDBS的参数，即可制备两光子四量子比特杂化纠缠的团簇态.

除了上述态制备方面的拓展外,还可以利用该光路实现隐形传输.通过调整器件参数,获得两光子三自由度的类W态.该态由两个光子组成,具有二体纠缠的特性,将两个光子分别发送给Alice和Bob，Alice和Bob再分别做相应的探测操作,就可以完美实现以两光子类W态为传输信道的量子隐形传输.这类态也可用于一些以多自由度纠缠态为资源的量子协议,实现所需的量子通信.

6 结论

本文提出了一个可以制备两光子三自由度纠缠W态的方案.该方案制备的W态是以自由空间为传输信道,包含3个自由度：OAM、偏振和路径.3个自由度的混合纠缠,相当于被编码在3个不同的Hilbert空间,它具有强纠缠性以及传输更多量子信息的能力.尤其对于OAM自由度,携带OAM的光束更有利于在自由空间传输信息.因此,本文制备的多自由度W态相对于单一自由度编码的W态更具优势：有限的量子资源具有更高的信道容量和更有效的量子信息处理能力,并且能与多种量子网络兼容.本方案的W态制备效率为1/2, 相对于以往W态制备的效率有了显著提升.最后,提出了一个实验探测方案,用来检测是否成功制备了W态.根据纯三量子比特态可由其两个二量子比特约化态唯一决定的理论,计算得到该三量子比特态的密度矩阵与三量子比特W态的密度矩阵是相同的,理论验证W态的成功制备.