一种嵌套式X 型结构的高阻尼隔振器性能研究

2021-03-05刘国勇赵鹏鹏刘海平沈洪兴

湖南大学学报（自然科学版） 2021年2期

刘国勇，赵鹏鹏，刘海平†，沈洪兴

（1.北京科技大学机械工程学院，北京 100083；2.中科院微小卫星创新研究院，上海 201210）

近年，航空航天领域工程装备日益向轻质、高速、重载等方向发展；尤其在国防领域，武器装备面临高速度、高机动、高隐身、高精度等迫切的发展需求.因此，广泛应用具有高比强度、高比刚度、且具备优良的减振缓冲特点的结构和材料已成必然.目前，在这类结构和材料中，重点追求其在质量约束条件下的高刚度特性，由此引起的结构振动与声辐射问题愈发突出.

通常，传统的振动控制方法一般期望更小的谐振频率以实现更好的隔振性能，如准零刚度隔振器[1-3].但是，选择较小的谐振频率意味着较小的系统刚度，即系统的静态承载能力不足，同时对于准零刚度隔振器而言，通常会有系统复杂和严重的稳定性问题.综上，为了保证在系统刚度不减小的情况下，提高阻尼输出，研究人员开展了大量研究工作.

Shi 等[4]利用磁铁间的不同配置设计了两种磁性负刚度阻尼器；Antoniadis 等[5-7]在单自由度线性隔振器基础上，通过插入负刚度元件实现隔振系统的超阻尼输出特性，并完成了深入的理论研究.Yang 等[8]结合金字塔点阵和黏性流体模块作为芯子结构，黏弹阻尼片和碳纤维板作为面板提出一种可实现高刚度高阻尼的夹层结构板，研究表明这种结构在不减小结构刚度的条件下有增大阻尼的效果.董光旭等[9]提出一种磁性负刚度机构可实现高刚度超阻尼的隔振效果.刘海平等[10-11]设计了一种基于碳纤维复合材料的轻量化高刚度高阻尼结构，并通过试验验证了该设计方法的有效性.显然，以上研究工作主要通过引入非线性刚度特征实现对系统输出阻尼的放大.

Jing 等[12-15]借鉴仿生学原理提出基于X 型结构的新型隔振器并进行了系统深入的研究.研究发现通过X 型结构对隔振系统引入的几何非线性特征可以极大改善隔振器的阻尼和刚度输出特性.综合利用X 型结构隔振器的概念，设计并完成了多种满足不同使用场景的新型X 型隔振器，如基于鸟类胫骨的非线性阻尼特性，提出的非线性高阻尼隔振器；适用于航天器在轨维修与服务的减隔振捕获机构；基于人体的被动隔振系统，提出的具有大负载能力和低动态刚度的耦合非线性隔振器；用于减小建筑工程领域手持冲击钻作业过程产生的振动冲击载荷对操作人员的影响开发的新型减振缓冲型外骨骼结构.但是，以上研究工作提出的隔振器均通过多层串联X 型结构且沿水平方向安装一个线性弹簧，未考虑水平方向同时安装弹簧元件和阻尼元件的影响.

综上，本文首次提出一种基于嵌套式X 型结构的高阻尼隔振器.通过建立其运动微分方程，采用谐波平衡法给出其稳态谐波激励下的解析解.为了便于对比，综合评价安装高阻尼隔振器前后隔振系统谐振频率和谐振峰值变化特征.在选择相同结构设计参数条件下，嵌套式X 型结构高阻尼隔振器较之常规线性隔振器在谐振频率不降低的情况下谐振峰值更小.此外，通过对嵌套式X 型结构高阻尼隔振器多个设计参数的灵活调整，可满足不同应用场景的减隔振需求，并且具备可折叠、操作灵活、易于制造和实施等优点.

1 动力学建模

基于嵌套式X 型结构高阻尼隔振器的力学模型，如图1 所示.其中，实线为考虑负载时的静平衡状态，虚线为未考虑负载时的初始状态.kv为隔振器沿垂直方向的支承弹簧刚度；kh为内嵌X 型结构内部的弹簧刚度；l1为外部X 型结构刚性杆长度，l2为内部X 型结构刚性杆长度；8 根刚性杆均以铰接的方式连接；外部刚性杆与水平轴y 的初始夹角为θ1，外部刚性铰接杆与水平轴的夹角变量为φ1，如图1 所示；内部刚性杆与水平轴y 的初始夹角为θ2，内部刚性铰接杆与水平轴的夹角变量为φ2，如图2 所示；c 为阻尼系数；受外部载荷F 作用；t 为时间.假设，垂直向上为x 轴正方向，水平方向向右为y 轴正方向.

图1 内嵌式X 型结构高阻尼隔振器力学模型Fig.1 Mechanical model of high-damping isolator with nested X-shaped structure

图2 X 型结构运动前后相对位移关系图Fig.2 Relative displacement diagram of X-shaped structure before and after motion

由图1 所示力学模型，得到系统沿x 轴方向的运动方程为：

外部X 型机构几何关系式为：

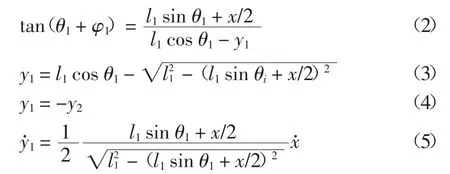
内部X 型机构几何关系式为：

将式（2）-（11）代入式（1）整理可得：

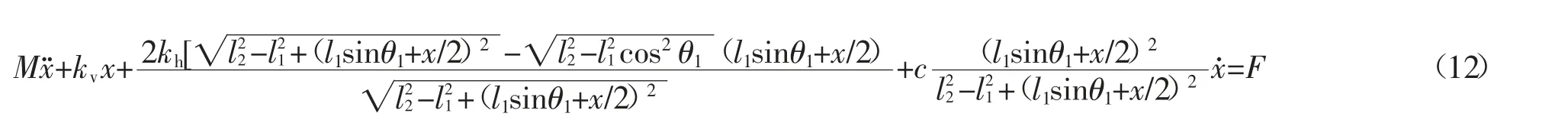
为了求解力激励条件下系统的时域响应，定义变量x1=x，x2=同时，假设质量块所受激励为F=F0cos ωt.代入式（12）可得：

采用四阶龙格库塔法求解微分方程组（13），即可得到隔振系统的时域响应结果.这部分工作主要为了验证下面推导的解析结果.

以下求解该隔振系统的频域解.

为了方便计算，需要对式（12）进行化简，定义函数：

由于函数f1（x）和f2（x）在x=0 处连续，将式（14）和式（15）分别在零平衡位置采用三阶泰勒级数展开，可得：

为了方便计算，对式（23）引入无量纲化参数，具体定义如下：

式中：ωn为隔振系统固有圆频率，τ 为无量纲时间，γ为隔振器纵横刚度比，Ω 为频率比，u 为无量纲长度，ξ 为阻尼比，f0为无量纲激励力幅值，λ 为刚性铰接杆杆长比.

将式（15）和式（16）代入式（12）中，并进行无量纲化后，可得：

采用谐波平衡法对式（26）进行求解.假设其稳态解为：

式中，u0为位移幅值.

将式（32）代入式（26），并消除高次谐波项，可得：

将式（33）中的谐波项展开，并令方程两边的一次谐波项系数相等，可得：

将式（34）和式（35）化简整理后可得：

在式（36）中，直接求解u0比较困难，为了求解该隔振系统的幅频响应，将式（35）写成关于频率比Ω的形式：

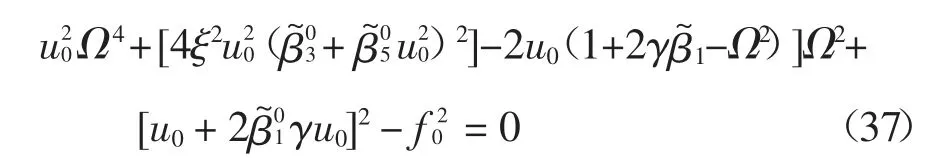
则可以解得力激励条件下隔振系统的幅频响应：

式中：Ω 上标f 代表力激励，下标则表示幅频响应曲线由两部分组成，两条曲线的交点即为响应幅值的最大值.

由式（34）和式（35）可解得力激励条件下隔振系统的相频响应.为了方便表示，令：

2 等效阻尼分析

高阻尼隔振系统的等效阻尼力为：

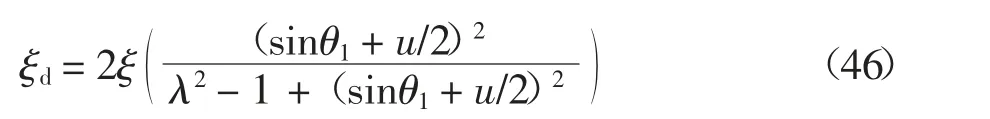
式中：ξd为高阻尼隔振器的无量纲等效阻尼.

无量纲等效阻尼与无量纲位移曲线，如图3 所示.由图可见，虚线为线性隔振器的阻尼特性曲线，为一定值；实线则为高阻尼隔振器的等效阻尼.对比发现，随着位移增大，高阻尼隔振器等效阻尼逐渐减小且呈现非线性减小的变化规律；但是，分析位移范围内，高阻尼隔振器的等效阻尼均显著大于线性隔振器.

图3 等效阻尼Fig.3 Equivalent damping

3 隔振效果评估

为了验证高阻尼隔振器的隔振效果，采用力传递率作为评价指标.力传递率定义为传递到基础上的力幅值和激励幅值之比，即：

式中：Tf为力位移传递率，ftr为通过隔振器传递到基础上的力，f0为激励力.

对于常规线性隔振器，容易得到力传递率为

通过高阻尼隔振器传递到基础的力可以由达朗贝尔原理求得：

式中：F 为激励力，FN为地面支持力，在此处隔振系统传递到基础的力与地面支持力等大反向，M 为质量块质量，a 为惯性质量的加速度.由式（49）即可得传递到基础的力：

为了方便计算，对式（50）进行无量纲化处理：

将式（49）无量纲化后，采用线性叠加方法，整理得到：

将式（52）代入式（47），得到高阻尼隔振器的力传递率为：

由式（53），即可得到高阻尼隔振器的力传递率曲线Ω-Tf.同时，为了验证高阻尼隔振器解析解的正确性，利用式（13）采用四阶龙格库塔法给出时域数值解.

选择高阻尼隔振器的初始设计参数为c=5 N·s/m，θ1=60°，M=1 kg，F=1 N，kv=2 000 N/m，λ=0.6，γ=0.02.分别得到常规线性隔振器和高阻尼隔振器的力传递率曲线，如图4 所示.同时，为了便于对比，图上还给出数值计算结果.

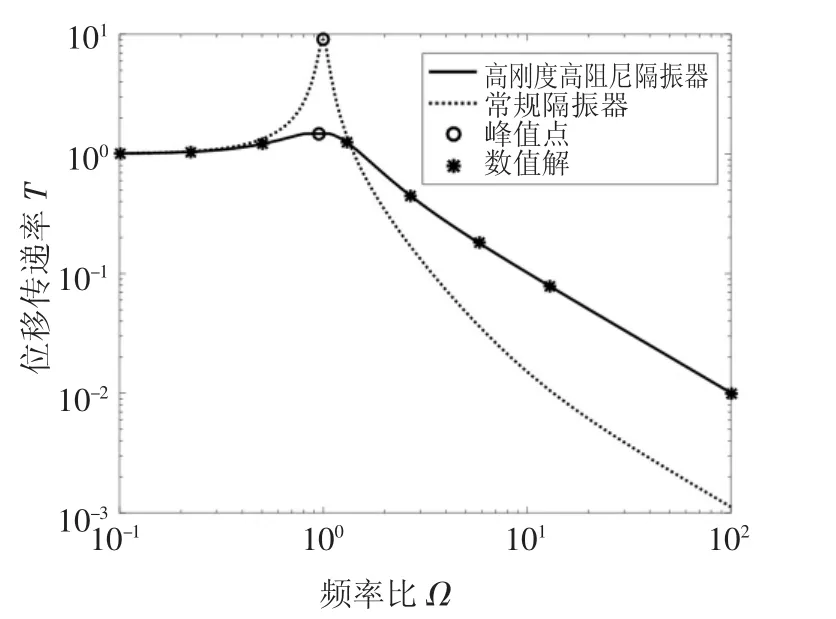
图4 不同隔振器力传递率曲线Fig.4 Force transmissibility curves for different isolators

由图可见，高阻尼隔振器的数值解和解析解保持一致，证明其频域解析解正确.与常规线性隔振器相比，力传递率曲线峰值得到显著衰减，且峰值频率未发生显著变化.由此表明实现了设计目标：即隔振系统刚度不减小的同时系统阻尼得到显著增大.

4 实验验证

为了验证高阻尼隔振器理论模型和设计方法的有效性，进一步完成了高阻尼隔振器动态力学性能测试，高阻尼隔振器实验件如图5 所示.其中，惯性质量m=2.3 kg；杆长l1=0.2 m；杆长l2=0.12 m；初始倾角θ1=60°；垂向弹簧刚度kv=4 000 N/m；水平弹簧刚度kh=800 N/m.需要说明，嵌套式X 型结构隔振器实验件的阻尼主要来自连接部位的摩擦阻尼和材料阻尼，未单独插入阻尼元件.

图5 实验件照片Fig.5 Photo of the test sample

测试系统主要包括：激振器、信号采集仪、信号发生器、功率放大器、计算机.实验状态如图6 所示，激振器在实验件顶部施加激励，模拟解析模型中的力激励，在实验件的顶部和底部分别连接一力传感器，分别检测输入与输出的力.

图6 实验状态Fig.6 Test status

测试过程中，采样频率为256 Hz；信号发生器的下限频率为5 Hz，上限频率为100 Hz，采用线性扫频，扫频时间60 s.

实验所得力传递率曲线与解析计算结果如图7所示.由图可见，力传递率谐振频率约为10 Hz，谐振峰值约为2.7；解析计算结果与数据变化规律良好一致；在中高频段，受实验件高频局部模态影响，实验所得传递率曲线出现波动；进而，导致解析结果与实测数据曲线出现差异.

图7 实验与解析力传递率曲线Fig.7 Force transmissibility curves of the experimental and analytical results

5 设计参数灵敏度分析

5.1 阻尼比ξ

保持其他设计参数固定不变，分别选择阻尼比ξ为0.02、0.05、0.10，得到力传递率曲线，如图8 所示.由图可见，随着阻尼比增大，力传递率谐振峰值被显著减小；当阻尼比为0.10 时实现了系统无谐振峰的响应效果.此外，受阻尼比增大影响，阻尼隔振器力传递率曲线在高频的衰减效果变差.

图8 不同阻尼比对应的力传递率Fig.8 Force transmissibility curves for different damping ratios

5.2 刚度比γ

仅考虑刚度比变化的影响，分别选择刚度比γ为-0.1、0.02 和0.1，高阻尼隔振器的力传递率曲线，如图9 所示.可见，刚度比为-0.1 时，可实现无谐振峰的隔振效果；而且，随着刚度比增大，力传递率谐振频率峰值增大；同时，峰值频率向高频移动.此外，刚度比对高阻尼隔振器力传递率特性的影响主要集中于谐振频率附近频段，即不同刚度比对应力传递率幅值在低频和高频范围趋于一致.