复合材料整流罩声学等效建模与低频隔声性能研究

李航行，吴邵庆，2，沈 林

（1.东南大学 工程力学系，江苏 南京 211189；2.东南大学 空天机械动力学研究所，江苏 南京 211189；3.上海宇航系统工程研究所，上海 201109）

0 引言

火箭发射过程中会遇到恶劣的动力学环境，气流与火箭整流罩的相互作用会产生气动噪声，外部噪声透过整流罩传播到内部，形成整流罩的内声场环境。整流罩内的一些电子设备对声、热［1］的敏感度较高，如果内部声场环境过于恶劣，将会引起整流罩内电子设备的功能失效。因此，开展火箭整流罩在发射过程中的声振响应和内声场环境预示，对整流罩降噪研究和优化设计，以及罩内设备的环境适应性分析具有重要的意义。整流罩外部噪声呈宽带、随机的特征，针对噪声激励下的结构声振分析，不同频段有不同的方法。低频段一般采用有限元⁃有限元，或者有限元⁃边界元的方法。相较前者，有限元⁃边界元方法［2］具有计算量小、精度高等优点；高频段一般采用统计能量法（SEA），统计能量法［3］能够用于复杂结构的高频响应预示，但是一般只能获取子系统上的平均能量，且在低频范围内计算精度较差；中频则一般采用混合建模法，如有限元⁃统计能量法［4］、有限元⁃模态能量法［5］等。噪声环境下的声振响应预示，是开展整流罩隔声研究的基础。

在整流罩的隔声方面，传统利用增加多孔材料提高隔声性能的方法对高频噪声具有较好的抑制效果［6］。低频段噪声由于抑制难度大，逐渐成为近年来研究的热点。开展低频噪声的抑制研究，首先需要开展低频段的声振分析。然而，目前火箭整流罩舱壁大量采用复合材料蜂窝夹芯结构，基于精细化蜂窝夹芯结构模型的声振分析，但是因计算量过大而无法在真实整流罩结构上应用，因此，需要开展高精度等效建模方法研究，利用等效模型完成整流罩结构低频声振响应预示。针对蜂窝夹芯板的等效研究主要集中在力学参数等效方面，目前主要有3 种等效方案，分别为三明治夹芯板理论［7］、等效板理论［8］和蜂窝板理论［9］。三明治夹芯板理论只对蜂窝芯进行等效，其中考虑了蜂窝芯抵抗横向剪切变形的能力和面内刚度，上下面板则服从Kirchhoff假设，忽略上下面板抵抗横向剪切变形的能力，从而将蜂窝芯等效为几何尺寸不变的均质正交各项异性层。姜东等［10］利用三明治夹芯板理论开展了蜂窝板的等效建模，并利用模型修正技术对蜂窝板前四阶固有频率开展修正，修正后模型频率均值误差小于5%，标准差结果接近试验值，可准确反映蜂窝板动态特性的离散性。等效板理论忽略蜂窝芯层面内剪切模量，将蜂窝夹芯板弯曲问题等效为横向各项同性单层板弯曲问题，根据刚度相等、质量相等推导出等效板的等效参数，从而将整个蜂窝夹芯板等效为等刚度均质各项同性板。蜂窝板理论考虑了蜂窝夹芯和上下面板的面内和面外力学性质，利用REDDY 低阶剪切理论和哈密顿原理等可以求出等效板的等效参数，从而将整个蜂窝夹芯板等效为等刚度、同尺寸均质正交各向异性板。

针对整流罩上使用的复合材料蜂窝夹芯结构，本研究利用三明治夹芯板理论等效蜂窝芯，然后利用蜂窝板理论进一步将蜂窝夹芯结构等效为各向异性板，在保证声学分析精度的同时提高分析效率。基于上述等效方法实现复合材料整流罩结构的力/声学等效建模，并进一步基于等效模型开展了整流罩的低频声振分析，预测了整流罩的内声场环境，评价了其隔声量，为整流罩的降噪研究提供参考。

1 复合材料蜂窝夹芯板等效建模及隔声分析

1.1 复合材料蜂窝夹芯板力/声学等效

整流罩用复合材料蜂窝夹芯板由上下玻璃钢面板和中间Nomex 纸蜂窝芯3 部分组成的，结构示意图如图1 所示。图中，d为上下面板的厚度，2h为蜂窝芯的厚度，t为Nomex 纸的厚度，l为正六边形的边长，a、b为选取矩形板的长和宽。为获得其力/声学等效模型，采用蜂窝板理论将蜂窝夹芯板等效为均质正交各向异性板，获取其等效力学参数。等效过程分为两步：首先对纸蜂窝芯进行等效；然后基于等效蜂窝芯对夹芯板进行等效。

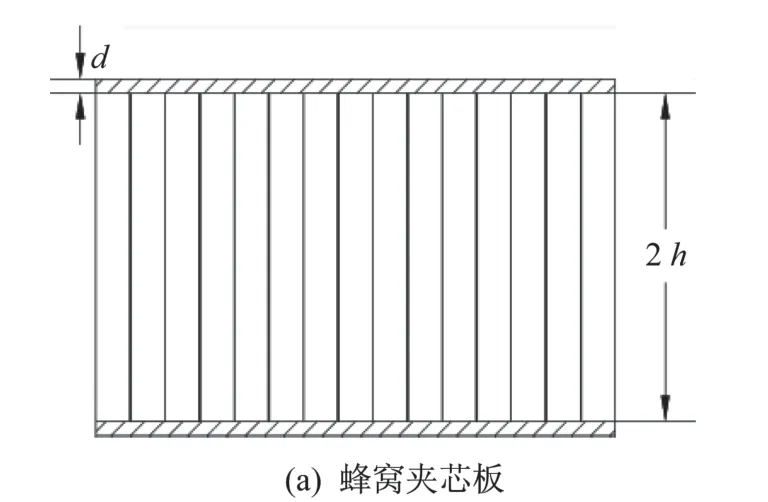
图1 蜂窝夹芯板结构示意图Fig.1 Structural diagram of a honeycomb sandwich panel

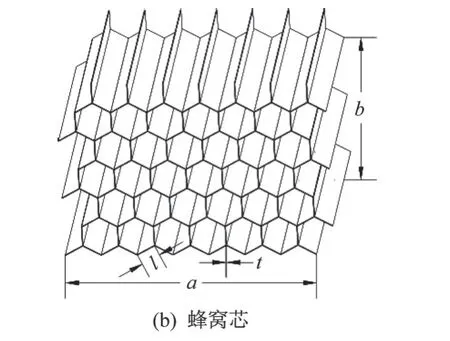
续图1 蜂窝夹芯板结构示意图Continue fig.1 Structural diagram of a honeycomb sandwich panel

对蜂窝芯的等效采用三明治夹芯板理论，其等效参数可以由如下公式得到：

式 中：E1、E2、G12分别为Nomex 纸的面 内两个方向的杨氏模量和剪切模量；ρs为Nomex 纸的密度；Ecx、Ecy、Ecz为蜂窝芯3 个方向上的等效杨氏模量；Gcxy、Gcyz、Gcxz为蜂窝芯在3 个面内的等效剪切模量；ρc为蜂窝芯等效密度；νcxy为面内等效泊松比。

在等效蜂窝芯的基础上，运用蜂窝板理论获得蜂窝夹芯板的等效力学参数为

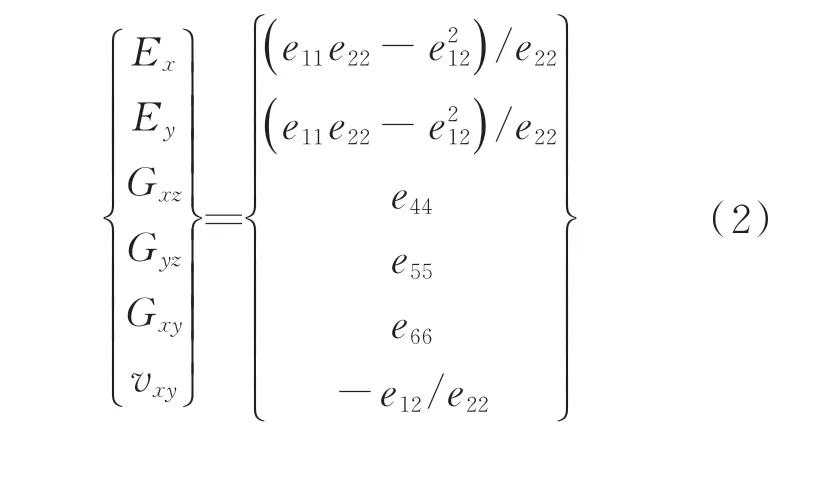
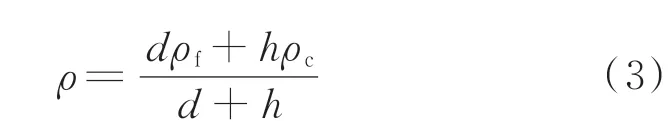
式中：Ex、Ey为板的面内等效杨氏模量；Gxy、Gxz、Gyz为板的等效剪切模量；νxy为等效泊松比；ρ为夹芯板的等效密度；ρf为上下面板的质量密度；eij为

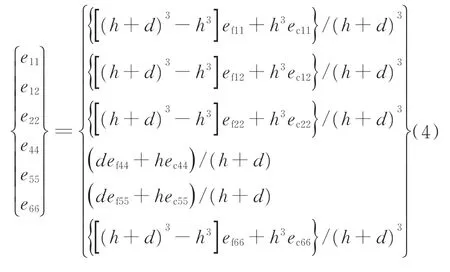
式中：efij、ecij分别为上下面板和芯层的刚度系数，可表示为

式中：Ef、Gf、νf分别为上下面板的杨氏模量、剪切模量和泊松比；K为影响系数，根据工程实际或实验取值于（0～1）［11］，表示蒙皮横向剪切的影响程度。

1.2 蜂窝夹芯板的声学等效与声传递损失计算

蜂窝夹芯板传声示意图如图2 所示。当入射波入射到蜂窝夹芯板上时，在入射一侧会产生反射声压，在另一侧会产生透射声压。

声学分析中常引入声传递损失（STL）度量结构的隔声性能，定义为入射声功率与透射声功率比值的对数关系：

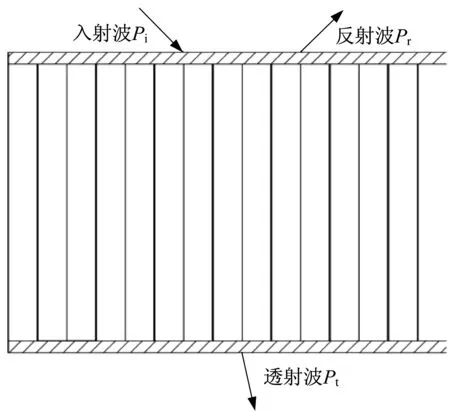
图2 蜂窝夹芯板传声示意图Fig.2 Sound transmission diagram of honeycomb sandwich panel

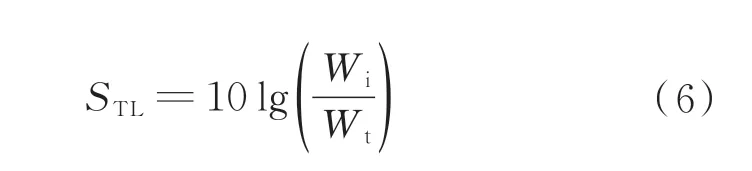
式中：Wi为入射声功率；Wt为透射声功率。

针对蜂窝夹芯板结构可转化为声阻抗与介质特性阻抗的形式［12-13］：

式中：Z为蜂窝夹芯板的声阻抗；ρ0为空气密度；c为声波在空气中的传播速度；φ=0°为声波的入射角。蜂窝夹芯板的声阻抗Z可表示为

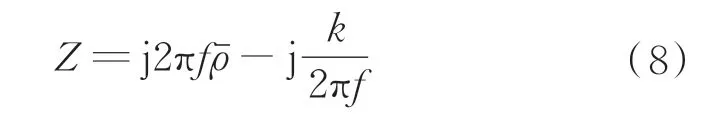
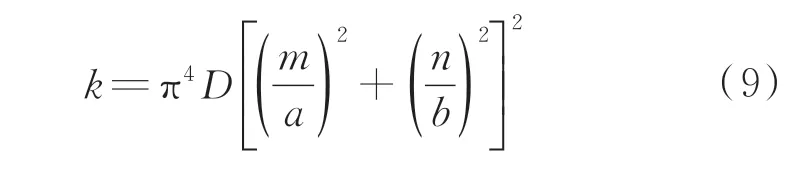
式中：a、b为蜂窝板的几何尺寸；m、n为一系列的整数（m，n=1，2，…）；结构弯曲刚度D为

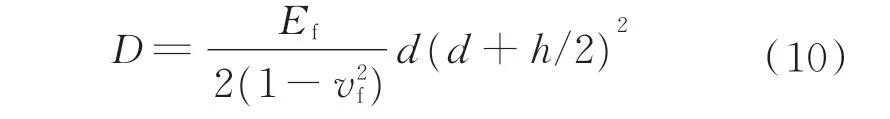
定义结构第m、n阶固有频率为fmn=，可得蜂窝夹芯板最终声阻抗表达式为

将式（11）代入式（7）可得蜂窝夹芯板隔声量的表达式为

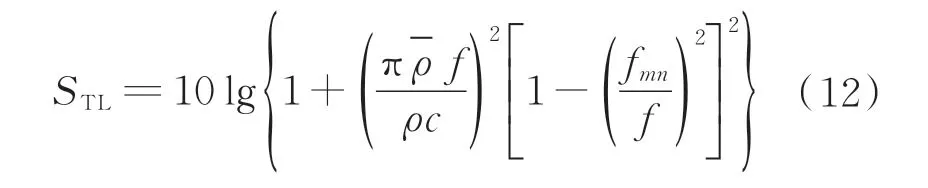
将蜂窝夹芯板参数及由1.1 节得到的等效板参数分别代入式（12），可得到精细化模型及等效板模型的隔声量。由式（12）可以看出，当精细化模型和等效板模型的固有频率一致时，对应的隔声量也一致。而力学等效可以保证等效板模型与精细化模型固有频率的一致性。因此，当完成蜂窝夹芯板的力学等效时，对应的隔声特性也即等效。

1.3 整流罩内声场预示

由于蜂窝板结构较为复杂，基于精细化建模的整流罩结构模型开展内声场预示计算量过大，难以实施。为降低模型计算量，首先对整流罩舱壁复合材料蜂窝夹芯板开展等效建模。由于蜂窝板的声学特性依赖于力学特性，因此，先对蜂窝板进行力学等效，在此基础上进行声学等效，利用蜂窝板精细化模型的模态分析和声学分析结果验证等效模型的准确性。基于力/声学等效的蜂窝板模型，开展整流罩结构的低频声振响应分析，完成内声场预示和隔声分析。值得一提的是，结构的声学特性与其力学特性紧密关联。当力学等效具有较好精度时，结构在相同激励下会产生高度相似的振动响应，从而在结构另外一侧会产生相似的声场。因此，利用蜂窝板验证了等效模型声学分析结果的精度之后，可以利用等效板模型以及有限元⁃边界元方法，获得具有较好精度的整流罩结构声振响应。具体实现流程图如图3 所示。

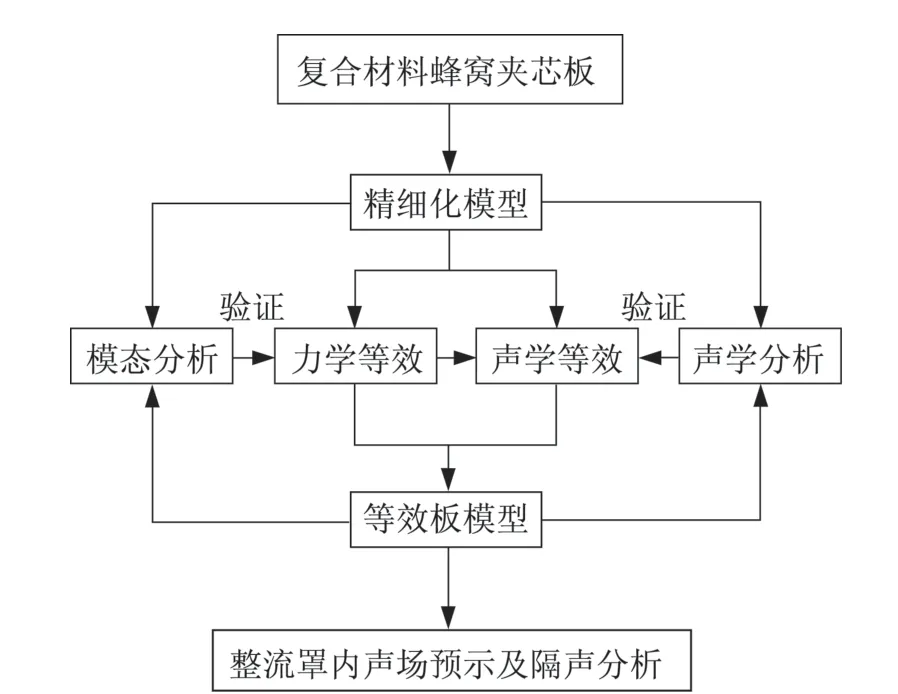
图3 整流罩内声场预示流程图Fig.3 Flow chart of internal sound field prediction for fairing

2 仿真分析

2.1 蜂窝夹芯板力学等效

本文研究对象为整流罩用复合材料蜂窝夹芯板，尺寸和材料参数见表1 和表2。各尺寸变量的物理含义如图1 所示。利用1.1 节中的等效方法，将表1 中的参数代入式（2），可以获取表3 所示的等效板的力学参数。分别对精细化模型和等效板模型建立有限元模型进行模态分析，见表4。建立复合材料蜂窝夹芯板的精细化模型，模型采用壳单元建模，单元数为720 000，节点数为400 000，如图4 所示。建立等效板模型，模型采用实体单元建模，单元数为6 000，节点数为8 000，如图5 所示，等效后模型自由度数大大降低。

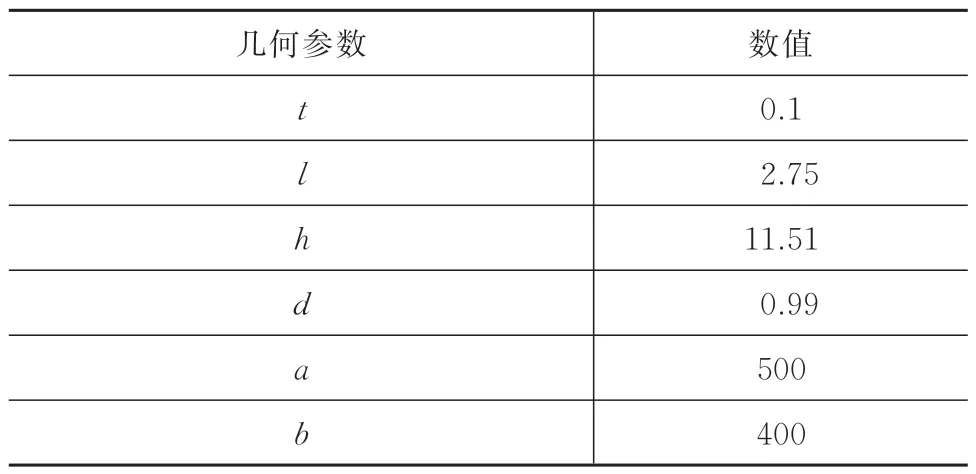
表1 蜂窝夹芯板几何参数Tab.1 Geometric parameters of honeycomb sandwich panel mm

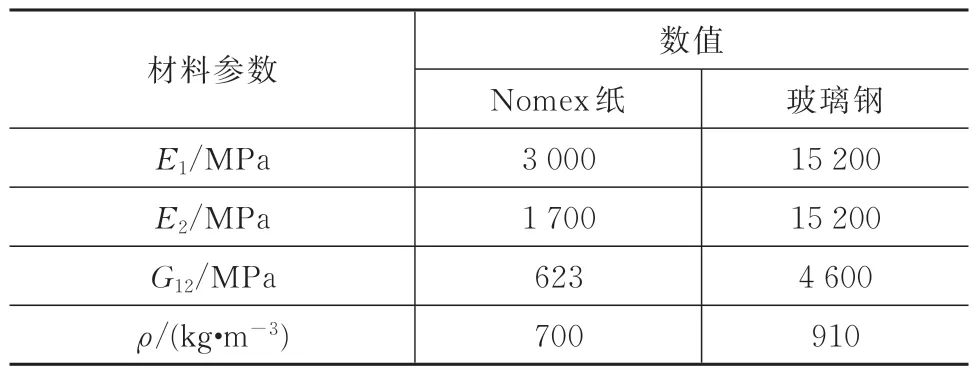
表2 蜂窝夹芯板材料参数Tab.2 Materialparametersofhoneycomb sandwich panel

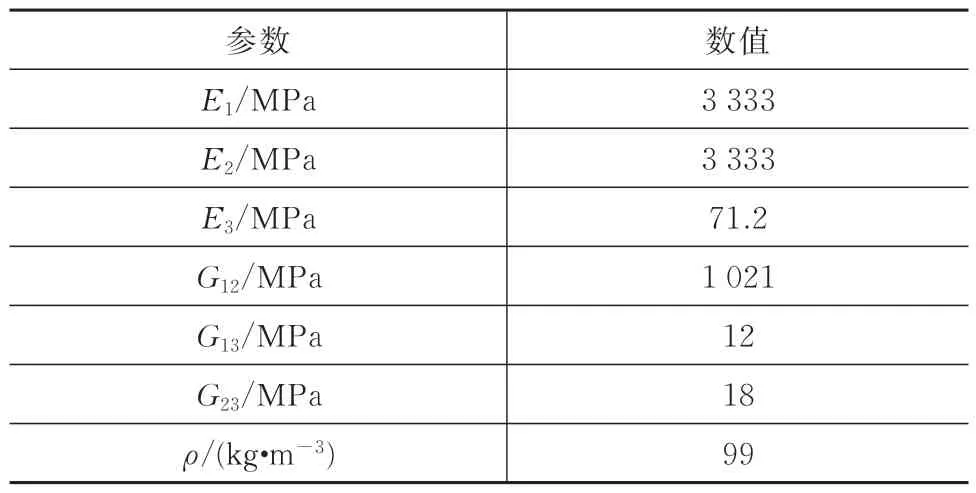
表3 等效板参数Tab.3 Parameters of the equivalent plate

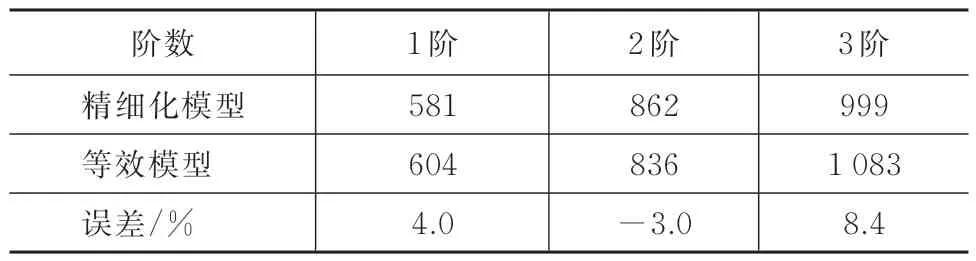
表4 模态频率对比Tab.4 Comparison of modal frequencies

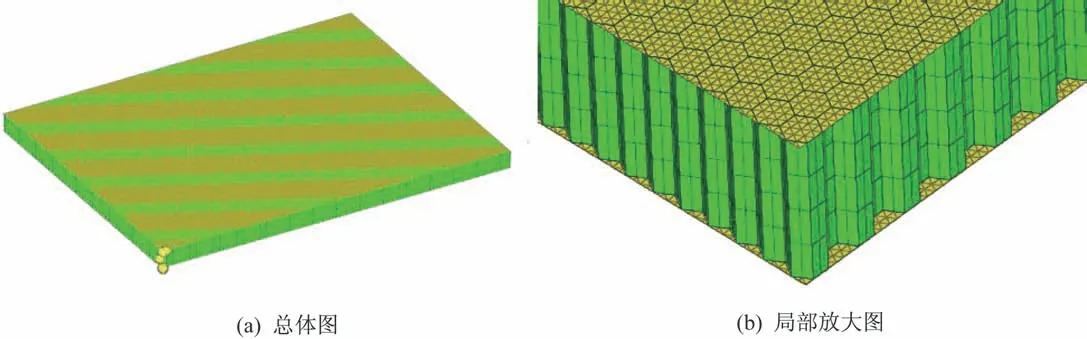
图4 精细化模型Fig.4 Refined model

图5 等效板模型Fig.5 Equivalent plate model

由表4 和表5 中的结果可以看出，等效模型和精细化模型的第1、2 阶模态频率的误差在5%以内，第3 阶模态频率的误差在10%以内，前3 阶模态振型具有较好的一致性。

在低频范围内，本文提供的等效方案可以在实现减小模型计算量的同时保持较高的分析精度，为复合材料整流罩结构低频声振响应预示提供可行的方法。

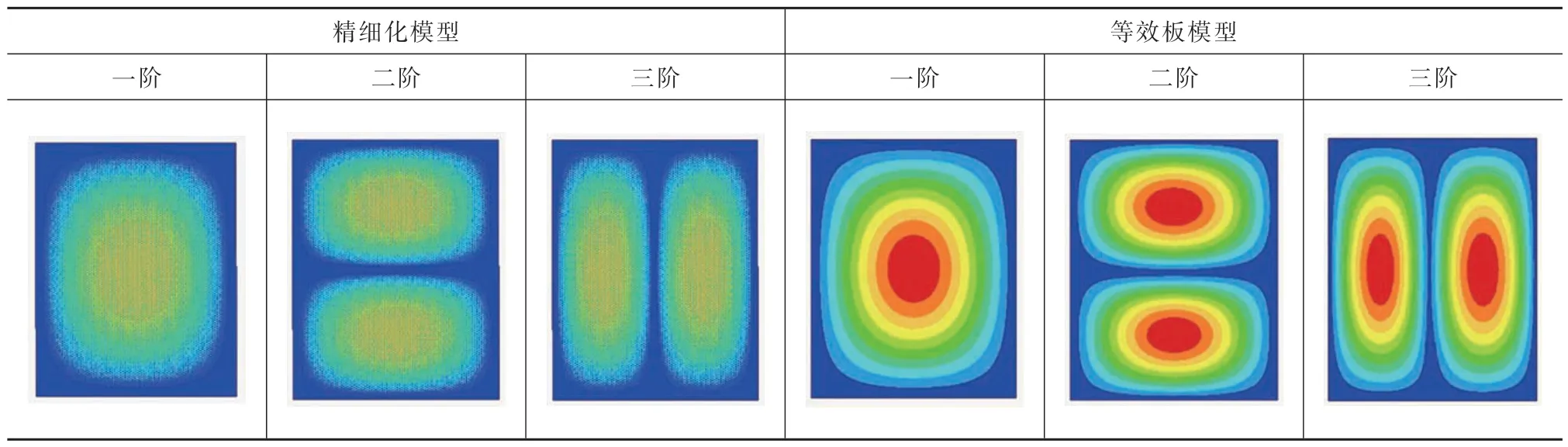
表5 模态振型对比Tab.5 Comparison of model shapes

2.2 蜂窝夹芯板声学等效

声波从板的一侧传播到另一侧有两种途径：一种是面板振动引起蜂窝芯内部空气振动，通过声振耦合的方式将声波传播到板的另一侧；另一种是通过蜂窝芯与上下面板的振动耦合将声波传播到另一侧。由于声振耦合是弱耦合［14］，本研究中在声振分析模型中不考虑内部空气的声固耦合效应。

在对结构进行声学分析时，一般要求最大网格尺寸小于计算最高频率处波长的1/6。本文最高分析频率选为3 000 Hz。考虑到声在空气中传播的速度为340 m·s-1，模型网格最大尺寸应小于18.9 mm，实际建模中，将网格尺寸控制在15 mm 以内。

基于商业软件LMS Virtual.Lab，采用间接边界元（IBEM）的方法对模型进行声学分析。有限元分析中需要3 种网格：结构网格、边界元网格、场点网格。将上节建立的有限元模型导入作为结构网格，边界元网格在Hypermesh 软件中建立，场点网格直接在LMS Virtual.Lab 软件中生成。为了防止声波的衍射作用，模型中添加障板，以使声波只能通过蜂窝夹芯板传播到另一侧，分析模型如图6 所示。

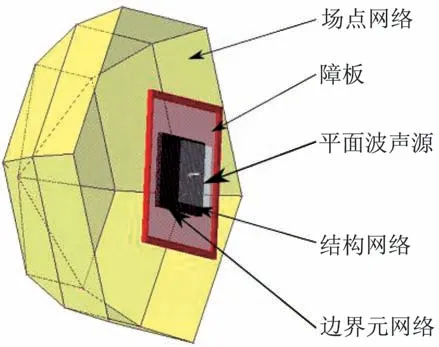
图6 声学数值模型图Fig.6 Model of acoustic numerical simulation

模型声学边界条件为平面波，对于平面波其入射功率可表示为

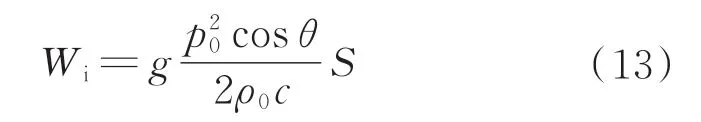
式中：p0=1 Pa 为入射波幅值；φ=0°为入射角度；ρ0=1.225 kg·m-3为空气的密度；c=340 m·s-1为声波在空气中的速度；S为入射表面的面积，本文建立的模型为a·b=0.2 m2。因此，可求得入射声功率为2.4×10-4W。

建立声学有限元模型，研究频率为100～3 000 Hz，步长设置为10 Hz。将入射声功率和透射声功率代入式（6）便可得到模型的隔声量，结果如图7 所示。对于有限大隔声板，从0 Hz 到第一个隔声谷之间为劲度控制区，这个区域的隔声效果与板的边界条件、几何尺寸和板的动态特性有关；从第一个隔声谷到隔声曲线停止波动，这一区域为阻尼控制区，这一区域的隔声曲线受结构阻尼影响较大。第一个隔声谷是由于板的共振引起的，随着频率的增加，达到板的共振频率，板的振动加剧从而引起相邻空气的振动，使得隔声量急剧降低。由图7 可看出，隔声量曲线有3 个隔声峰和隔声谷。第一个隔声谷对应板的第1 阶固有频率，是由于入射波频率与板的固有频率一致，导致板的共振引起的。在隔声谷附近频率段误差普遍较大，误差在±25%以上，这是由于隔声谷附近曲线斜率较大，曲线稍微的偏移便会导致较大的误差。其他频率段误差在±20%范围内分布。第一个隔声谷之前误差较小，小于2%；第一个隔声谷之后误差较大，且频率越高，误差相对就越大。这是由于等效式（2）在高频段误差较大引起。为减小误差，可针对式（2）进行修正。本研究关注整流罩段低频内声场，图7 显示采用1.1 节中的等效板模型在低频段误差较小。

图7 隔声量曲线Fig.7 Sound insulation curve

2.3 整流罩结构声场分析与隔声量评估

整流罩模态分析是其声振分析的基础。对包含卫星的某复合材料整流罩结构，开展基于等效板模型的有限元建模以及模态分析。模态分析的边界条件为倒锥段底部固支，结果见表6。表中，第1、2 阶为卫星结构的对称模态，第3、4阶为整流罩的对称模态。

火箭整流罩内噪声环境主要受两方面影响：一是起飞时发动机的强烈喷流；另一个是跨音速时的气动载荷环境。目前针对整流罩内声场的研究主要采用统计能量法［15-16］，但该方法在低频段计算精度差，因此本文采用有限元-边界元的方法研究整流罩低频隔声性能。针对整流罩结构开展精细化建模和分析的计算量过于庞大，本文提出的基于力/声学等效模型的声振分析具有计算效率的优势。

本文采用混响场模拟火箭外部声学环境，载荷施加在整流罩的球头和冯卡门段。由于通过增加多孔材料的方法在高频段有较好的降噪效果，而低频段降噪难度大，为揭示整流罩内声场环境，本文将研究频率设为10～355 Hz。将整流罩模态分析的有限元模型导入作为结构网格；在Hypermesh 软件中建立边界元网格，同时保证边界元网格最大尺寸不超过160 mm，以满足声学网格尺寸不超过研究最高频率波长的1/6 的要求。采用有限元-边界元的方法对模型进行声振分析，同时在倒锥段底部添加障板模拟全反射的硬边界条件。由于卫星分布在整流罩的圆柱段，因此，分别在整流罩圆柱段内外取面场点计算整流罩内外声功率，结果如图8 所示。

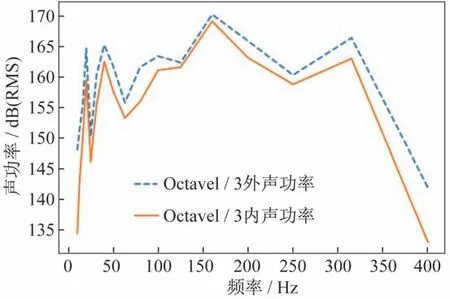
图8 整流罩内外声功率1/3 倍频程曲线Fig.8 One-third octave curve of the internal and external sound power of the fairing

由图8 可看出，内外声功率的前两个峰值就分别对应了整流罩的两阶模态频率，整流罩内声场环境在160 Hz 附近最为恶劣，声功率达到了165 dB。恶劣的声学环境可能会导致内部电子设备的失效，因此应主要针对该频段进行降噪分析。在20 Hz、40 Hz、300 Hz 附近声学环境较为恶劣，声功率达到160 dB，针对该频段也应展开降噪分析，以改善罩内声学环境。

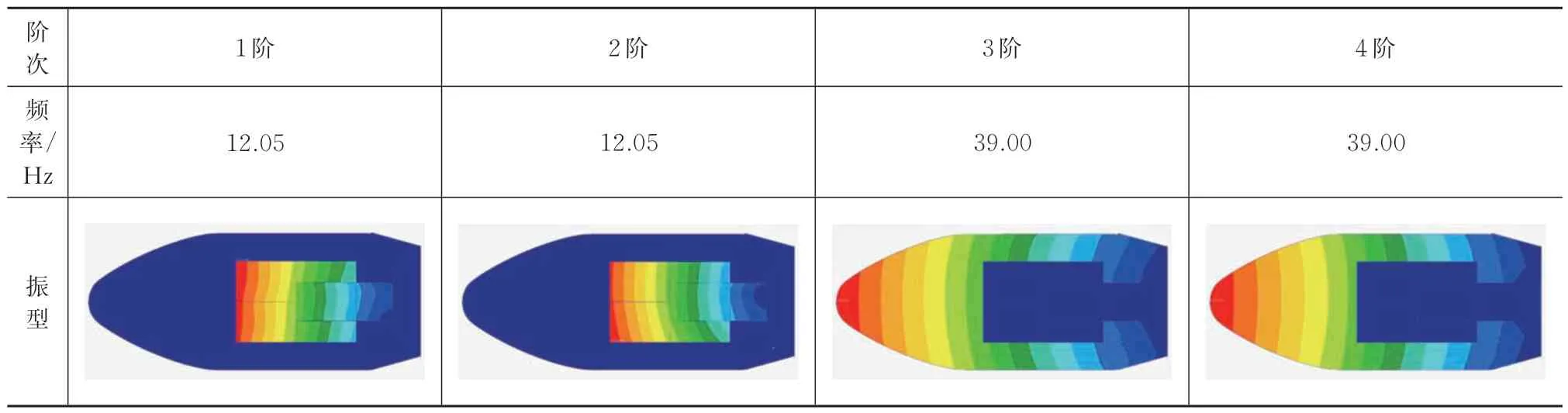
表6 整流罩固支边界下模态分析结果Tab.6 Modal analysis results of fairing under fixed boundary condition

将内外声功率代入式（6）可得整流罩的隔声量，如图9 所示。图9 中结果显示整流罩在低频段的声传递损失不到0.5 dB。在10～355 Hz 频段，内外总声功率级相差3.2 dB，隔声效果并不理想，应通过进一步的降噪措施进行低频段降噪。

整流罩内在某些特征频率处的声功率云图如图10 所示。由图10 可以看出，不同频率下的内声场环境并不相同，且声场的分布并不均匀。由于内部卫星的耦合及反射作用，在一些区域会产生较高的声功率级，因此，应通过降噪手段，改善该区域声学环境。

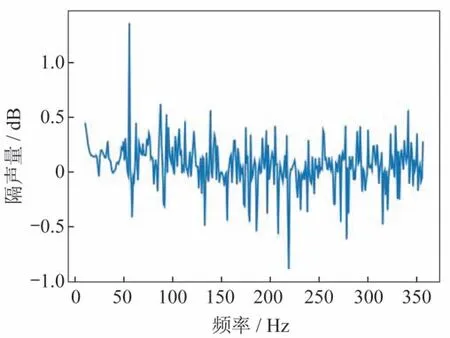
图9 整流罩隔声量曲线Fig.9 Sound transmission loss curve of the fairing

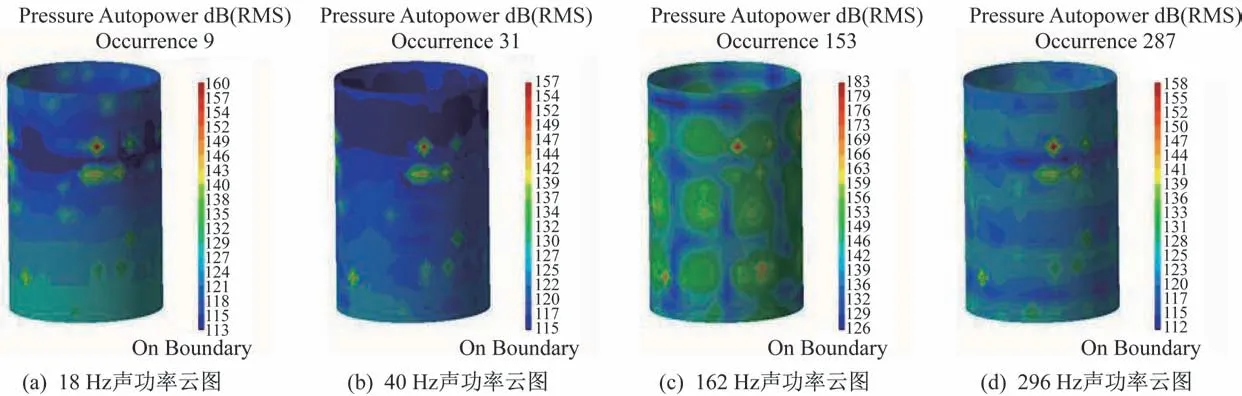
图10 整流罩内声功率云图Fig.10 Cloud chart of the internal acoustic power for the fairing

3 结束语

本文基于复合材料蜂窝板的力/声学等效模型，开展了复合材料整流罩的低频声振响应分析，预测了整流罩内声场环境。结果表明，低阶等效板模型和精细化模型的力学及声学特性较为吻合，高阶存在较大误差。在低频段，采用本文提供的等效方案开展复杂整流罩结构的低频声振分析具有较好的精度。整流罩内声场环境预示结果表明：在160 Hz 频率附近声学环境最为恶劣，应针对该段频率开展降噪研究。整流罩结构在低频段的整体隔声效果并不理想，声传递损失不到0.5 dB，在10～355 Hz 频段，内外总声功率级相差3.2 dB，应通过降噪措施进行低频段声学降噪。