冲击/周期载荷作用下分布式调谐质量阻尼器对响应控制的影响

宋吉祥，吴 炜，严定帮，郭双喜，陈伟民

（1.中国科学院 力学研究所，北京 100190；2.中国空空导弹研究院，河南 洛阳 471009；3.中国科学院大学 工程科学学院，北京 100049）

0 引言

悬臂梁是一种常见的工程结构，例如飞机机翼、吊车悬臂、混凝土泵车的悬臂、高压电电塔悬臂、航天机械臂［1］、太阳翼［2］等。由于悬臂梁仅在一端有固定约束，结构刚度低，所以在受动力荷载作用时，位移响应大，应力幅值偏高，容易导致结构疲劳破坏。因此，如何有效抑制悬臂梁的振动响应一直是工程上研究的热点和难点。

事实上，关于悬臂梁/板振动控制的研究已有大量成果。例如，针对飞行器固定机翼的振动控制和颤振抑制，压电结构被广泛使用，并且取得了良好 的成果［3-10］。FEI［11］使用基于xPC 目 标实时系统的主动控制方法，控制压电作用器，抑制悬臂梁的振动。许睿等［12］基于模糊控制方法对柔性太阳能帆板振动进行了控制，数值结果表明采用变论域自适应模糊控制比简单模糊控制的效果更好，但是采用压电材料不仅需要有外部电源且主动控制算法复杂，而被动控制由于不需要外部能量，并且构造简单、易于维护，因而得到广泛关注。例如，调谐质量阻尼器（Tuned Mass Damper，TMD）应用于建筑结构、桥梁、海洋工程、抗震工程［13-16］。BAE 等［17］将涡流阻尼器与调谐质量阻尼器组合在一起控制悬臂梁振动，发现即使不调谐，该装置依然可以增强TMD 的阻尼效果。VERMA 等［18］在安装单桩式海上风力涡轮机的叶片时，通过在风塔上安装TMD，降低风塔与叶片的相对冲击速度达到了40%。在已有研究中，针对悬臂梁的振动控制研究，一般都采用冲击荷载［5-6，19］，实际工程中载荷情况复杂，不仅有冲击荷载，周期载荷也是一种很常见的载荷情况。并且悬臂梁结构在服役时，振动通常以低阶模态为主导。所以本文针对常见的悬臂梁结构，考虑两种载荷激励，即低阶弯曲频率的周期激励荷载和冲击荷载，通过安装多个TMD，控制悬臂梁的振动位移，以期降低应力幅值，提高结构的疲劳寿命。

本文推导了安装N个TMD 的悬臂梁动力学偏微分方程；使用有限元法对控制偏微分方程进行离散，转为代数方程，便于求解计算；以一种典型尺寸的悬臂梁模型为例，进行周期荷载和冲击荷载作用，研究TMD 对振动抑制效果；最后结果显示，TMD 可以有效抑制悬臂梁的振动。

1 理论模型

1.1 含多TMD 的悬臂梁控制方程

一个安装N个TMD 的悬臂梁结构示意图如图1 所示。悬臂梁为等截面均匀梁，TMD 包括1 个质量块、1 个弹簧和1 个阻尼器。对于不考虑剪切变形的欧拉伯努利梁，其运动控制方程为

式中：y为悬臂梁的竖向位移；z为悬臂梁的横向位置；EI为悬臂梁的抗弯刚度；mz为悬臂梁的单位长度质量；c为阻尼系数；t为时间；f(s，t)为在s处t时刻施加的外部激励荷载；fTMD，i(z，t)为第i个TMD对悬臂梁的作用力；mTMD，i、cTMD，i、yTMD，i(s，t)分别为第i个TMD 的质量、阻尼系数和位移；δ(z-s)为狄利克雷函数，其表达式为

悬臂梁的一端固定，一端悬臂，边界条件为

图1 安装TMD 的悬臂梁示意图Fig.1 Schematic diagram of cantilever beam with TMD

1.2 基于FE 的多TMD 悬臂梁动响应求解

本文采用有限元法对式（1）和式（2）进行离散，建立如下代数方程组：

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Y为位移矩阵；F为外部激励荷载矩阵；FTMD为N个TMD 对悬臂 梁的作 用力矩 阵；KTMD、CTMD、YTMD(s，t)、MTMD分 别为N个TMD 的刚度矩阵、阻尼矩阵、位移矩阵和质量矩阵。

阻尼系数采用Rayleigh 阻尼计算，公式如下：

式中：a0和a1为常系数。

式中：ωn为第n阶模态自振频率。一般通过两个关心的自振模态的振型阻尼比ξ计算获得a0和a1。

动力学方程组求解使用Newmark-β方法，a=0.5，β=0.25，时间总长1 s，时间步长Δt取第4 阶自振频率ω4的1/20。Newmark-β方法如下：

式中：等效刚度矩阵和等效荷载向量分别为

2 算例和数值结果分析

通过数值算例，具体分析分布式调谐质量阻尼器对悬臂梁振动的抑制效果。结构参数见表1，悬臂梁在自重的作用下，悬臂端最大位移为0.0014 m，所以认为悬臂梁处于线弹性状态。

表1 悬臂梁的结构参数Tab.1 Structural parameters of cantilever beam

悬臂梁的自振频率与自振模态形状如图2 所示，根据结构动力学原理可知，在振动中低频模态更容易被激发并在响应中占主导，为了提高TMD抑制振动的效果，设计TMD 的自振频率应尽量与控制悬臂梁的目标频率相同，以达到共振。本文设计TMD 参数时，以TMD 的自振频率与控制悬臂梁的目标频率相同为设计原则，设计针对前4 阶模态的TMD 物理参数，并且在相应模态振型最大位移位置处安装TMD。另外，为了避免同一位置安装多个TMD 导致相互碰撞，对TMD 安装的位置进行了调整，放置模态振型的第2 个最值位置，如图2 所示。TMD 的物理参数见表2。

假设1 阶模态16.55 Hz 和2 阶模态103.72 Hz的模态阻尼比ξ为0.05，根据式（8），可得Rayleigh阻尼系数a0=8.968，a1=1.30×10-4。

3 荷载作用下的振动抑制效果

3.1 周期荷载下的振动抑制效果

悬臂端竖向正弦荷载为

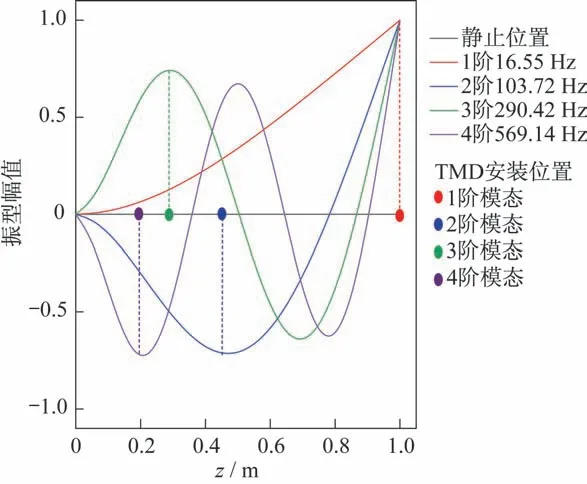
图2 悬臂梁前4 阶振型、自振频率及TMD 安装位置Fig.2 The first 4 modes of cantilever beam，natural frequency and TMD installation position

这里考虑与前4 阶振动频率相同的荷载频率达到共振，增大响应位移。荷载频率ωi为第i阶弯曲自振频率，ω1=103.99 rad/s，ω2=651.69 rad/s，ω3=1 824.76 rad/s，ω4=3 576.01 rad/s。荷载激励幅值f1=5 N，f2=150 N，f3=3 500 N，f4=15 000 N，荷载激励幅值不同主要是为了使前4 阶振动幅值比较接近。

通过悬臂梁响应时域分析，根据悬臂端位移时程结果，研究设计不同TMD 数量对悬臂端位移的振动控制效果的影响，如图3 所示。考虑4 个工况，工况（a）为一个TMD 安装在1.00 m 处控制1 阶振动的情况，工况（b）为2个TMD 分别安装在1.00 m 和0.45 m处控制1、2 阶振动的情况，工况（c）为3 个TMD 分别安装在1.0 m、0.45 m、0.30 m 处控制1、2、3 阶振动的情况，工况（c）为4 个TMD 安装在1.00 m、0.45 m、0.30 m 和0.20 m 处控制1、2、3、4阶振动的情况。

表2 TMD 的物理参数Tab.2 Physical parameters of TMD

如图3 所示，在激励荷载作用下位移响应很快上升到最大，然后随着时间的增加，位移逐渐变小，达到稳定状态。在4 个工况下，控制前的悬臂端位移均大于控制后的悬臂端位移，说明TMD 可以抑制悬臂梁的振动。为了定量分析控制效果，选取稳定段0.8 s～1.0 s 的最大位移进行比较，控制前为0.045 m，抑制后4 个工况的位移依次为0.024 0 m、0.022 2 m、0.021 8 m 和0.021 2 m，控制位移降低比例分别是46.67%、51.11%、51.56%和52.89%。由此可知，采用单个TMD（即工况（a））的抑制效果最低，而随着安装TMD 数量的增加，抑制效果逐渐增加并不断改善，直至采用4 个TMD（工况（d））时抑制效果达到最佳，因此，安装TMD 数量越多抑制效果也越好。但是，如果关注单个TMD 的控制效率，即平均单个TMD 抑制位移效果的值分别为46.67%、25.56%、17.19%、13.22%，可见随着安装TMD 的数量增加，平均单个TMD 抑制位移效果的值明显下降。TMD 的安装数量需要进行合理的计算，并非越多越好。

观察响应频谱，对稳定段0.8 s～1.0 s 的悬臂端位移进行傅里叶变换，如图4 所示。尽管控制前后的前四阶自振频率变化较小，但是频谱峰值显著降低。尤其是第1 阶、第2 阶弯曲自振频率的幅值，随着TMD 的数量增加显著降低。但是第3 阶、第4 阶弯曲自振频率的幅值，TMD 的数量增加并没有降低幅值。采用1 个TMD 控制第1 阶弯矩振动的效果最为显著，因为增加的TMD 与悬臂梁组成了新的动力系统，系统的质量增加，自振频率降低，与激励荷载频率不再一致，共振效果减弱。采用多个TMD 虽然进一步降低了自振频率，因自振频率距离激励荷载频率较远，以致从悬臂梁传递到TMD的能量较小，故悬臂梁振动幅值下降缓慢。

3.2 冲击荷载下的振动抑制效果

瞬时冲击荷载如图5 所示，安装不同的TMD 数量对悬臂端位移的振动响应结果如图6 所示。

图3 安装不同的TMD 数量对悬臂端位移的振动控制Fig.3 Vibration control of cantilever end displacement by installing different TMD numbers

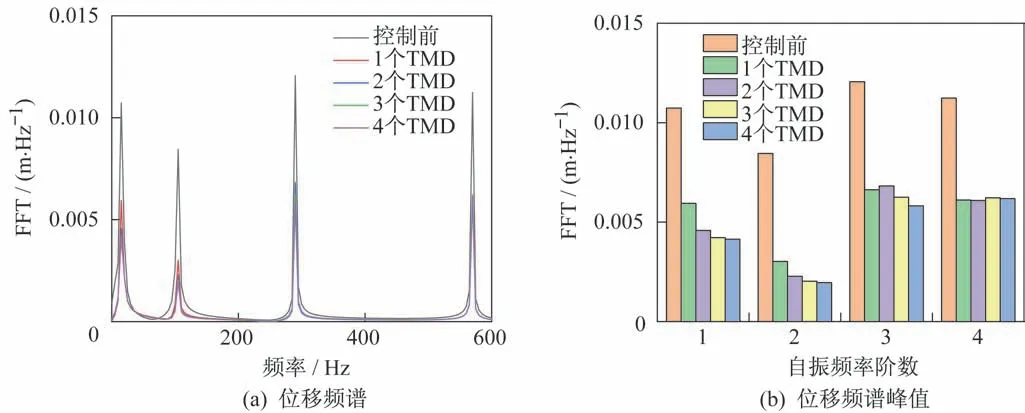
图4 在0.8 s～1.0 s 悬臂端的竖向位移频谱和峰值Fig.4 The spectrum and peak values of the vertical displacement of the cantilever end in 0.8 s～1.0 s

图5 冲击荷载Fig.5 Impact load

结构在第1 个振动周期达到位移最大，随着时间的增加，在结构阻尼的作用下，位移缓慢降低。当安装TMD 后，第1 个振动周期的位移减小，最大位移降低比例分别12.31%、11.59%、14.63%、14.87%。可见，TMD 可以减小悬臂梁在冲击荷载作用下的最大位移。但是，从0.2 s 之后，安装TMD的悬臂端位移比没有安装TMD 的悬臂端位移大，因为从悬臂梁传导到TMD 的能量没有被迅速消耗，可以增加TMD 的阻尼增加能量消耗速度，降低位移幅值。所以，TMD 不能迅速抑制悬臂梁的自由衰减振动。

图6 安装不同的TMD 数量对悬臂端位移的振动控制Fig.6 Vibration control of cantilever end displacement by installing different TMD numbers

悬臂端位移谱如图7 所示。图中可知，悬臂梁的自由衰减运动中仅有1 阶和2 阶弯曲振动响应较大，并且1 阶弯曲振动幅值远大于2 阶弯曲振动幅值，3、4 阶弯曲等高阶模态难以被冲击载荷激励。当 安装1 个或者2 个TMD 时，悬臂 梁⁃TMD 系 统的1 阶弯曲自振频率幅值相差较小，悬臂端位移没有2 阶弯曲自振频率参与振动；当安装3 个或者4 个TMD 时，系统一阶弯曲自振频率幅值接近，频率比悬臂梁的1 阶弯曲自振频率低，但是在60 Hz 处频率幅值大于零，可能是由于悬臂梁将能量传递给第3 个、第4 个TMD。TMD 在通过自身阻尼耗散能量的过程中，对悬臂梁产生了激励荷载。

图7 悬臂端位移频谱Fig.7 Spectrum of cantilever end displacement

在冲击荷载作用下，振动响应以一阶弯曲为主，因为高阶振动频率需要的激励荷载幅值较大，而且频率高，单位时间内的能量需求高，所以高阶振动频率难以激发。即使高阶振动被激发，在没有稳定的激励荷载的作用下，由于阻尼效应，也会迅速耗散静止。因此，悬臂梁的振动控制应该关注于低阶模态。

4 结束语

本文研究了采用多个分布式调谐质量阻尼器（TMD）对悬臂梁进行振动的控制，通过数值分析，分别研究了周期荷载和冲击荷载作用下梁振动控制的效果。数值结果表明：

1）TMD 可以有效抑制悬臂梁的振动。在周期荷载作用下，悬臂端的位移降低46.67%。在冲击荷载作用下，悬臂端最大位移降低12.31%，但是不能迅速抑制自由衰减振动。

2）在周期荷载和冲击荷载作用下，由于结构1 阶弯曲自振频率远低于其他阶弯曲自振频率，激发高阶模态所需要的荷载幅值远大于1 阶；考虑到结构低阶弯曲振动在响应中占主导，控制悬臂梁的振动应该关注于低阶模态。

3）TMD 的分布形式对控制效果有重要的影响。当使用1 个TMD 抑制振动时，建议TMD 最好安装在悬臂端部，且自振频率应与悬臂梁1 阶弯曲频率相等；采用多个TMD 可以提高控制效果，但需要安装不同的位置以防碰撞，但平均单个TMD 抑制效果降低。