基于统一强度理论的热-力耦合作用下圆形隧洞的弹塑性解析解
2021-03-03惠强姜海波张玉洁
惠强,姜海波,张玉洁
(石河子大学水利建筑工程学院,新疆 石河子 832003)
地下洞室工程进行开挖后,其附近一定范围内岩体应力分布及力学性质会发生显著变化,当应力超过围岩弹性峰值状态后,便会产生塑性变形[1]。分析开挖后围岩应力分布情况、确定塑性区范围对评价围岩稳定性及实际工程支护设计有重要意义。目前,关于围岩应力分布的弹塑性分析,大多是基于Mohr-Coulomb等单剪强度准则,如经典的Kastner方程便是基于Mohr-Coulomb准则推导得到的,因其形式简单而被广泛运用,但由于其忽略了中间主应力的影响,导致计算结果与实际情况有较大差别[2]。俞茂宏等[3-4]提出的统一强度理论很好弥补了单剪强度理论没有考虑中间主应力的不足,并讨论了该理论在围岩弹塑性分析的适用性。基于该理论,许多学者开展了关于围岩弹塑性分析的研究,陈立伟等[5]推导出考虑中间主应力影响的非均匀应力场的隧洞围岩塑性区边界线方程,刘怀付等[2]推导出考虑塑性软化影响的隧洞围岩应力、位移及塑性区半径表达式,昝月稳等[6]结合Hoek-Brown强度准则的优点提出了适用于岩体或节理化岩体的非线性统一强度准则,谷拴成等[7]探讨了第一主应力为不同应力情况下围岩应力的分布情况。
综上所述,目前考虑中间主应力影响的围岩弹塑性解析解大多只考虑了单一应力场,但地下岩体赋存于应力场、温度场等多场共存的复杂环境中,且当岩体承受的强度超过其峰值强度后其强度参数会发生显著的变化,从而影响岩体的应力分布,故只考虑单一应力场的解析解与实际存在较大的误差,另外,考虑热力共同作用及岩体软化的解析解研究相对较少。鉴于此,本文在上述研究的基础上,基于统一强度理论,同时考虑热力耦合、软化及中间主应力的影响,建立圆形隧洞围岩应力及塑性区范围解析表达式,结合算例分析不同中间主应力系数以及温度场对围岩应力分布的影响。
1 理论模型
1.1 力学模型
图1为隧洞围岩力学模型示意图,围岩为各向同性的均质岩体,根据围岩应力状态,将围岩分为塑性残余区、塑性软化区以及弹性区,文献[8-9]将塑性残余区称为破裂区或松动圈。垂直地应力与水平地应力相等,隧洞支护阻力均匀分布于隧洞内壁。假设隧洞无限长,可作平面应变问题处理。

图1 围岩力学模型
本文理论分析中的强度准则采用俞茂宏提出的统一强度准则[3],该准则中b为中间主应力对材料破坏的影响参数,其值范围为0≤b≤1,在取值范围内,统一强度准则近似于其它强度准则[10]。
为体现围岩的软化效应,本文理论分析中引用文献[11]中的应变软件模型。在应变软化的峰前阶段,塑性软化系数(即塑性剪切应变)为0,岩石处于弹性阶段;在应变软化的峰后阶段,塑性软化系数均大于0,当塑性软化系数小于岩石由塑性软化阶段进入塑性残余强度阶段的临界塑性软化系数(即临界塑性剪切应变)时,岩石处于塑性软化阶段,该阶段岩石粘聚力及内摩擦角值随着塑性剪切应变的增大而减少,其线性关系满足下面公式(1)、(2)[12];当塑性软化系数大于等于临界塑性软化系数时,岩石进入塑性残余阶段,此时岩石各项参数为峰后的残余参数。
(1)
(2)
式(1)、(2)中下标pv和rv分别表示处于峰值和残余状态下的岩石参数;η为塑性剪切应变,模型中将其定义为塑性软化系数;η*为临界塑性软化系数。
文献[13]假设加载卸载斜率相同的岩石全应力应变曲线,通过试验结果拟合得出临界塑性软化系数的计算公式为:
(3)
(4)
1.2 围岩温度场模型
隧洞温度应力主要分为以下三类[14]:由隧洞内部温度改变所产生的温度应力、由混凝土水化反应产生的温度应力、由隧洞内温度以年为周期的温度波动所产生的温度应力。本文采用稳态温度场来分析隧洞围岩的温度应力,不考虑混凝土衬砌,故上述三类应力中只考虑第一类温度应力。
隧洞开挖后,由于洞内温度改变造成围岩一定范围内出现变温区,在变温区以外,仍为原岩温度t1,文献[14]给出了隧洞围岩不受温度变化影响的半径计算公式。设隧洞开挖半径为R0,围岩变温区半径为R,可得围岩变温区温度边界条件为:
内边界:r=R0时,t=t0;
外边界:r=R时,t=t1。
其中t0为隧洞开挖后洞内温度,t1为原岩温度。根据变温区温度边界条件结合稳态温度场下围岩导热微分方程,可推得隧洞围岩变温区的温度分布方程。温度应力由自生温度应力和约束温度应力两部分组成[15],为耦合计算方便,本文统一压应力取正值,拉应力取负值。由于隧洞围岩恒温区内变温恒等于0,故恒温区内不产生自生温度应力,变温区自生温度应力计算公式可以根据变温区内温度分布方程以及无限长厚壁圆筒理论求得[14]。
由于隧洞围岩变温区与恒温区接触连续,故当变温区由于变温产生自生温度应力时,变温区与恒温区之间必然会产生一对均布的约束力Pt[14],约束温度应力由此产生。将求得的围岩变温区、恒温区自生温度应力和约束温度应力叠加,可得隧洞围岩总的温度应力方程,恒温区(r≫R)的为:

(5)
变温区(R0≪r (6) 式(6)中α为围岩线膨胀系数,μ为泊松比,上标vt表示变温区内温度应力,ct表示恒温区内温度应力。 在进行平面应变条件下圆形隧洞围岩的弹塑性分析时,当地应力侧压力系数等于1,即围岩处于均匀压力状态时,围岩径向应力、切向应力分别等于最小主应力、最大主应力[16]。考虑隧洞轴向应力,由于围岩径向应力、轴向应力、切向应力相互正交,可认为轴向应力等于中间主应力[3],同时在塑性状态下应力满足以下关系[3,5]: (7) 将式(1)、(2)、(3)、(7)代入式(2),整理得地应力各向等压条件下考虑应变软化的围岩统一强度理论公式为: σθ=σrA1+A2。 (8) 将式(8)与塑性区轴对称问题的平衡方程[17]联立求解得: (9) 式(9)中U1为待定常数。 (10) 式(10)中上标d表示塑性残余区。 (11) 式(11)中Rd为隧洞圆心至塑性残余区外边界的距离。 (12) 式(12)中上标s表示塑性软化区。 (13) 式(13)中Rp为隧洞圆心至塑性软化区外边界的距离。 积分常数待定的弹性应力一般解为: (14) 式(14)中U2、U3为待定常数,e表示弹性区。 (15) 再将解得的待定常数U2、U3代入式(14),得到弹性区的应力计算公式如下: (16) 由弹塑性接触面上关于切向应力相等条件[17],联立式(12)、(16),解得Rp表达式为 (17) 由式(13)、(17)可得: (18) 当b=0时,式(18)变为 (19) 将式(3)、(19)联立,解得 (20) 再将式(18)、(20)代入式(10)、(12)、(16),便可得到由临界塑性软化系数及相关岩石参数表达的考虑应变软化的岩石各状态下的应力表达式。 由上述分析可知,隧洞围岩从温度场角度分区可分为变温区和恒温区,从弹塑性角度分区可分为塑性残余区、塑性软化区和弹性区,故分以下三种情况进行耦合分析:变温区和恒温区交界面位于弹性区范围内;变温区和恒温区交界面位于塑性软化区范围内;变温区和恒温区交界面位于塑性残余区范围内。 (21) 式(21)中上标m表示由边界载荷产生的应力。 弹性应力可由温度和边界荷载产生的应力相加[19]求得,在变温区内的弹性应力为 (22) 在恒温区内的弹性应力为 (23) 计入温度应力的塑性区轴对称问题的平衡方程为 (24) (25) 将塑性残余区外边界条件代入式(25),得热力耦合情况下塑性残余区半径为: (26) 按照2.2中计算方法及边界条件,可得塑性软化区应力及塑性软化区半径表达式: (27) (28) 当r=Rp时,根据应力连续条件[19],解得热力耦合情况下地应力与塑性区半径的关系式如下: (29) 在该情况下,塑性残余区由于都处于变温区内,故应力和半径表达式与情况3.1时一样。塑性残余区由于变温恒温交界面的存在,以变温恒温交界面半径为分界分为两部分,其中,位于变温区范围内塑性软化区的应力计算公式为式(27)。将r=R处径向应力相等的条件代入式(8)、(24),得到位于恒温区的围岩塑性软化区应力表达式为: (30) 由于该情况下弹性区全部处于恒温区内,故弹性区应力表达式同式(23)。将式(23)和(30)联立,或根据塑性软化区外边界条件r=Rp时σθ=σpvθ,皆可求得塑性软化区半径。 在该情况下,位于变温区内的围岩塑性残余区应力计算公式也为式(25),将r=R处径向应力相等的条件代入式(8)、(24),得到位于恒温区内的围岩塑性残余区应力表达式为: (31) 将塑性残余区外边界条件代入式(31),可得该情况下塑性残余区半径。由于该情况下塑性软化区全部位于恒温区内,根据平衡方程式求得该情况下的塑性软化区应力和软化区半径表达式为式(12)、(13),弹性区温度应力为式(23)。 由上述理论分析可知,不同条件下圆形隧洞围岩应力状态及应力计算公式也不同。为了解不同工况、不同b值的情况下围岩应力的分布情况,通过下面算例进行分析。 某圆形水工引水隧洞,其开挖半径为2 m,支护力为0,岩石的弹性模量为7.5 GPa,岩石强度衰减模量为7.3 GPa,密度为2.5 g/cm3,泊松比为0.25,剪胀角为10°,峰值内摩擦角为37°,残余内摩擦角为30°,峰值粘聚力为1.3 MPa,残余粘聚力0.8 MPa,临界塑性软化系数为0.008,初始地应力为20 MPa,隧洞内边壁温度为20 ℃,原岩温度为60 ℃,热膨胀系数为5×10-6℃-1,比热为1.0 kJ/(kg·℃),导热系数为2.4 W/(m·℃)。 设仅有力的作用(工况一)、热-力共同作用(工况二)二种工况。为验证本文推导出公式的准确性,令内外温度相同,计算二种工况下围岩应力分布及塑性区范围,取中间主应力系数为0,统一强度准则退化为莫尔-库伦强度理论,当岩石力学参数不随应变发生软化,仅有力作用时围岩弹塑性区应力表达式参考文献[17],塑性区半径按修正的Fenner公式计算。围岩应力计算结果(图2)表明:本文与文献[17]方法计算的结果一致,塑性区半径计算结果也同为3.4 m,这证明了本文推导出公式的准确性。 图2 内外温度相同时围岩应力分布 取中间主应力系数等于0(莫尔-库伦强度理论)、0.25、0.5、0.75(介于0和1之间为各种加权强度理论)和1(双剪强度理论)[21]这五个参数,分别计算在这两种工况不同强度理论下(由中间主应力系数的取值体现)围岩的应力分布情况及塑性区大小,并对比分析其规律,结果见图3,其中横轴为位置半径与开挖半径的比值,当其为1时,表明该点位于开挖面。 图3 围岩中应力分布 从工况一取不同中间主应力系数时所得到的围岩应力分布情况(图3a)可以看出:围岩径向应力的整体趋势是随着围岩深度的增长不断升高,最后趋于原岩应力。随着中间主应力系数的增大,围岩径向应力逐渐增大,同时在塑性区内径向应力的变化速率也随着中间主应力系数的增大而增大,尤其是在塑性软化区内部,当中间主应力系数为0时,塑性软化区内围岩径向应力变化速率为2.46 MPa/m,当中间主应力系数为1时,变化速率为2.83 MPa/m,较中间主应力系数为0时增加15%。围岩切向应力的整体趋势是先快速升高,到达峰值后逐渐下降,最后同样趋于原岩应力。在塑性区范围内,随着中间主应力系数值的增大,围岩切向应力逐渐增大,而弹性区则逐渐减小。 工况二取不同中间主应力系数所得到的围岩应力分布情况(图3b)与工况一基本一致。 图4为不同中间主应力系数情况下工况一和工况二的围岩应力分布对比图,由图4可知:相比于只考虑力的作用(工况一),当热力共同作用时(工况二),由于温降产生拉应力,围岩径向应力均有所减小;在相同中间主应力系数的条件下,工况一和工况二的切向应力值会在某点重合,该点位于工况一的峰后位置,工况二的峰前位置,在该应力重合点之前,工况一的切向应力大于工况二的切向应力,在该应力重合点之后则相反,最终都趋于原岩应力,当中间主应力系数为0时,该重合点对应的半径值在5.7 m,当中间主应力系数为1时,该重合点对应的半径值在4.1 m处,表明随着中间主应力系数的增加,峰前阶段的围岩切向应力变化速率逐渐增加,峰值点逐渐向隧洞临空面移动。 图4 不同工况下围岩应力分布 图5为不同中间主应力系数工况一和工况二的峰值切向应力对比图。 图5 不同b值的峰值切向应力 由图5可知:随着中间主应力系数值的增加,围岩峰值切向应力逐渐增大,工况一情况下中间主应力系数为1时所对应的峰值切向应力(34.2 MPa)比中间主应力系数为0所对应的峰值切向应力(33.1 MPa)增加了4.2%,工况二情况下中间主应力系数为1所对应的峰值切向应力(34.5 MPa)比中间主应力系数为0所对应的峰值切向应力(32.9 MPa)增加了4.9%;与工况一相比,相同中间主应力系数的情况下,工况二的围岩峰值切向应力更小,表明热力共同作用下围岩的极限强度有所降低。 表1为不同中间主应力系数及不同工况下,塑性残余区、塑性软化区、塑性区半径对比。 由表1可知:随着中间主应力系数的增加,两种工况下塑性残余区、塑性软化区及塑性区半径均有所减少,这与范文等[22]研究的结论一致。在中间主应力系数相同的情况下,热力共同作用(工况二)所产生的塑性残余区、塑性软化区及塑性区半径均大于只有力作用(工况一)的情况:当中间主应力系数分别等于0、0.25、0.5、0.75和1时,对应的塑性区半径分别由仅有力作用情况时的3.1 m、2.5 m、2.2 m、2.0 m、1.8 m增加至热力共同作用情况时的3.83 m、3.04 m、2.59 m、2.30 m和2.09 m,增加了23.56%、19.63%、17.43%、15.98%、14.60%,平均增加了18.24%;塑性残余区半径、塑性软化区半径的变化趋势与上述相同,分别平均增大了19.78%和15.01%。考虑温度应力和不考虑温度应力时的塑性残余区、塑性软化区、塑性区半径存在较大差异,说明在实际工程中考虑温度应力的影响是有必要的;中间主应力系数越小,工况一和工况二所产生的塑性区半径越大,同时工况一和工况二的差异性越大,说明基本原理采用莫尔-库伦强度理论得到的结果相对保守,且相较仅有力作用的情况,热力共同作用的情况更易受中主应力效应的影响。 表1 不同中间主应力系数的分区半径对比 本文基于统一强度理论和弹塑性理论,考虑应变软化,通过改变中间主应力系数,推导出不同强度理论下单一应力场以及热力共同作用这两种工况中圆形隧洞围岩塑性残余区、塑性软化区边界线方程式以及周边围岩应力表达式。模型验证及算例计算分析结果表明: (1)随着中间主应力系数的增大,经计算得到的围岩应力变化速率逐渐增大,围岩峰值切向应力逐渐增大,塑性残余区、塑性软化区半径逐渐减小,工况一和工况二情况下中间主应力系数为1时相较中间主应力系数为0时,塑性区半径分别减少了41.24%和45.50%,表明不考虑中间主应力效应的计算结果相对保守,在一些情况下不能充分发挥围岩自身的强度。 (2)通过算例分析可知,热力共同作用与仅有力作用相比,塑性残余区、塑性软化区、塑性区半径平均各增大19.78%、15.01%、18.24%,表明在实际工程中考虑温度应力的影响是有必要的;围岩塑性区内应力均有所减小,弹性区内切向应力略大于仅有力作用时的切向应力,峰值切向应力则小于仅有力作用时的峰值切向应力。研究成果可为热力耦合作用下的圆形隧洞围岩应力分析以及塑性区范围预测提供理论参考,以便提出合理的支护范围。2 隧洞围岩塑性区及弹性区分析

2.1 塑性残余区分析
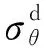
2.2 塑性软化区分析

2.3 弹性区分析

3 热力耦合分析
3.1 变温区和恒温区交界面位于弹性区范围内
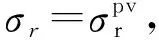

3.2 变温区和恒温区交界面位于塑性软化区范围内
3.3 变温区和恒温区交界面位于塑性残余区范围内
4 模型验证与算例分析
4.1 模型验证

4.2 算例及分析




5 结论
