可变起跳角度的球形跳跃机器人跳跃分析及其优化

,,,

(南京航空航天大学航天学院,江苏 南京 210016)

0 引言

跳跃运动是自然界中常见的动物运动方式。受到动物和人类跳跃运动敏捷性的启发，越来越多的国内外研究者开始研究跳跃运动并着手开发了各种各样的跳跃机器人。跳跃机器人的基本设计原理，是通过能量的积蓄在跳跃阶段完成快速的释放，短时间内克服机器人本体的重力势能，完成跳跃。跳跃的运动方式具有良好的越障功能，拓展了机器人的探索范围，在野外侦查、深空探测等领域有着广阔的应用前景。

跳跃机器人的分类方式有很多。依照产生跳跃的能量来源，跳跃机器人驱动方式可以分为机械能驱动、化学能驱动和场力作用等。利用机械弹性能的机器人常采用的是利用弹性元件和锁死释放机构结合完成能量储存释放[1-2]。化学能驱动利用化学反应过程中伴随着的能量变化，以及化学产物的生成，通过气体膨胀或者产生的热能进行驱动[3-4]。场力驱动的跳跃机器人往往是微小型的，利用如电磁场作用实现跳跃[5]。依据跳跃方式可以分为连续跳跃和间隔跳跃。连续跳跃机器人在完成一次跳跃之后马上进行下一次跳跃过程，这样可以利用上一次跳跃落地之后的动能等，提高能量的利用，但增加控制难度，对复杂跳跃环境的适应能力弱[6]。间隔跳跃的机器人在每次跳跃之间有时间间隔，往往可以进行姿态或者方向上的调整，设计难度相对较低，但是落地过程有大量能量浪费。

利用弹性元件储能实现跳跃功能具有结构简单、可靠性高和技术成熟等优点，而间隔式跳跃虽然有能量浪费，但是设计难度和控制难度都较小，具有较好的实用性。因此，项目组设计了一种具有间隔跳跃的机械能驱动跳跃机器人。

本文将进行该跳跃机器人的动力学分析，从机器人的结构和执行元件出发，目标是为了获得机器人的运动特点，了解机器人的运动性能，分析跳跃过程以及影响跳跃的因素，获得跳跃结果与控制量之间的关系[7-8]，从而提高机器人越障能力。

1 跳跃机器人结构设计

本文设计的跳跃机器人是一种利用压缩弹簧进行跳跃的机器人，机器人的结构如图1所示。

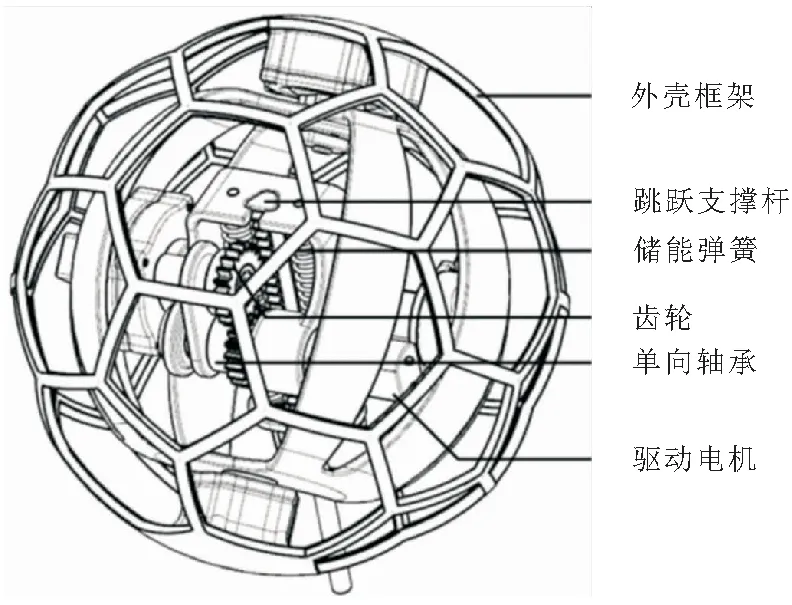
图1 跳跃机器人结构

该机器人由外壳框架和内部跳跃结构组成。外壳框架为多边形镂空结构，跳跃时，支撑腿从镂空孔伸出，接触地面完成跳跃。跳跃机构由跳跃支撑杆、储能弹簧、啮合齿轮、驱动电机、连接板和单向轴承等部分组成。弹簧弹性势能的储存和释放机构，由齿轮和单向轴承组成，实现该过程的原理是利用单向轴承内外圈正反转运动状态的不同，控制齿轮啮合和分离的不同状态。结构中的能量输出由2个电机负责：一个电机用于储能过程，拉动齿轮转动；另一个电机控制整个内部跳跃结构相对于地面的角度，通过调向机构，该机器人可以精确调整起跳角度。所设计的机器人基本参数如表1所示。

表1 机器人结构基本参数

2 跳跃机器人动力学分析

2.1 跳跃过程动力学建模

依据跳跃中机器人所处的位置状态，跳跃过程可以分为起跳过程、滞空过程和落地过程。

2.1.1 起跳过程

为了获得更清晰的机器人运动过程，沿跳跃支撑腿轴线所在平面对机器人结构进行剖视，获得如图2所示的简化结构。机器人的有效运动部分有2个:一个是可以改变内部跳跃结构相对地面夹角的转向结构P;另一个是可以在设定长度内进行压缩拉伸的弹簧结构Q。按照跳跃支撑腿相对于初始状态的位置，起跳过程又分为以下3个阶段。

a.第1阶段为弹跳支撑腿自由伸长阶段。在弹簧锁定机构打开之后，如图2a所示，弹簧推动跳跃支撑腿沿弹簧的轴线方向运动，直至跳跃支撑腿末端接触地面，达到图2b所示的状态。锁定结构打开之后，弹簧将处于可以伸展的状态，支撑腿接触地面的一端为自由端，弹簧会在这个方向上伸展。这个过程中，设弹簧长度由完全压缩情况下的rmin伸长至接触地面时的长度rtouch。当弹簧原长为r0，弹性系数为k，机器人整体的质量为M，跳跃支撑腿的质量为m时，接触瞬间支撑杆获得的能量为

(1)

整个过程理想地认为弹簧的弹性势能完全传递给一端自由的跳跃支撑腿，且不会对机器人产生影响。

b.第2阶段为跳跃腿与地面碰撞的过程。其发生在跳跃腿与地面的撞击过程，支撑腿的动量通过撞击的方式改变了方向，与此同时，支撑杆的一端接触地面，弹簧的另一端作用在球形机器人本体上，推动机器人本体向上运动。因为跳跃支撑腿在自由伸长阶段变化的长度很小，跳跃支撑腿获得的动能很少，若假设该碰撞过程为纯弹性碰撞，则支撑腿的动能会在之后的阶段转化为机器人的动能。

c.第3阶段为机器人球形本体起跳的过程，如图2c所示。该过程持续直至机器人完全脱离地面，从而进入之后的滞空过程。为了分析该过程中机器人的动力学状况，可以将机器人抽象为双质点弹簧模型，如图3所示。

图2 起跳过程弹簧状态变化

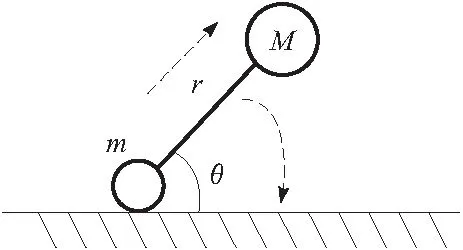
图3 双质点起跳模型

本文依据拉格朗日方程建立跳跃机器人起跳过程的动力学模型，首先假设跳跃支撑腿在起跳的过程中不发生滑动，在起跳过程中，弹簧推动机器人本体向上运动，同时在重力的作用下，机器人与地面的夹角也会发生变化，这里取系统的广义坐标为弹簧的长度r和机器人跳跃腿与地面的夹角θ，系统的动能T为机器人本体的动能，系统势能为弹簧势能与机器人本体重力势能之和，则有：

(2)

(3)

机器人本体的质量为M；跳跃腿的质量为m；机器人与地面起跳的夹角为θ；跳跃过程中弹簧的长度为r；弹簧的原长为r0。已知拉格朗日量L=T-V满足方程

(4)

qα为系统的广义坐标系r和θ；Qα为系统的广义力。不受其他外力影响的情况下，机器人的广义力为0，代入可得

(5)

得到系统的动力学方程为

(6)

为求解上述微分方程的值，需要分析系统的边界值。

在起跳结束的瞬间，因为机械结构的影响，机器人本体与跳跃支撑腿的速度会保持一致，也就是说，在那一瞬间，机器人本体的动能会分散到原本并没有运动的跳跃支撑腿上，即满足方程

v·M=vk·(M+m)

(7)

从而得到起跳之后真正的起跳瞬时速度，当支撑腿的质量很小时，该过程对速度的影响可以忽略不计。

2.1.2 滞空过程

假设起跳瞬间的状态设定为k，即文中所有下标为k的变量都是表示起跳瞬间的状态。此状态下机器人初始速度、角速度和角度分别为vk、ωk和θk。理想状态下，机器人起跳滞空过程的运动可等效为力学平抛模型，跳跃滞空的过程，竖直方向上的动能转化为重力势能，在达到最高点处，竖直方向上速度为0，由能量守恒可得

(8)

则小球起跳初始动能满足

(9)

机器人下落过程重力势能转化为动能，直至落地，理想状态下，整个平抛运动过程的轨迹为抛物线曲线，依据运动学公式

(10)

可以计算出运动的抛物线公式为

(11)

上述分析是将整个机器人看作质点，利用质点的平移来完成运动轨迹的计算。但实际上因为起跳阶段重力作用产生了初始的角速度，所以速度的方向角是不断变化的，起跳之后重力等效作用于质心上，角动量守恒，所以角速度会影响实际转化为重力势能的能量，即

θ=θk-ωkdt

(12)

在只考虑XY平面内的情况，这里假设机器人是由3个部分组成的，即本体、支撑腿和连接两者之间的短杆，本体的质量M要大于支撑腿的质量m，连杆的长度为l，质心O的位置位于本体和支撑腿之间，距离机器人本体和支撑腿质心的距离分别为l1和l2。假设起跳的瞬间机器人获得的速度大小为vk，起跳过程中，由于机器人同时受到弹簧弹力和自身重力的影响，vk并不经过质心，这样就会和机器人的轴线方向产生一定的夹角β。机器人的滞空过程如图4所示。

图4 存在初始角速度时的滞空过程

滞空过程中，机器人的运动可分解为平移和旋转两部分。机器人与水平面的夹角为

θ=θk-ωkt=θ0-β-ωkt

(13)

则滞空过程中，机器人水平和竖直运动速度分别为

(14)

质心的运动方程，直到第一次与地面碰撞的瞬间，竖直方向上应当满足高度变化为0，即表示为

(15)

求解出运动时间代入水平运动方程可以得到水平运动的公式，从而求得抛物线方程为

(16)

根据式(11)和式(16)，绘制并对比有无旋转情况下的跳跃轨迹，如图5所示。

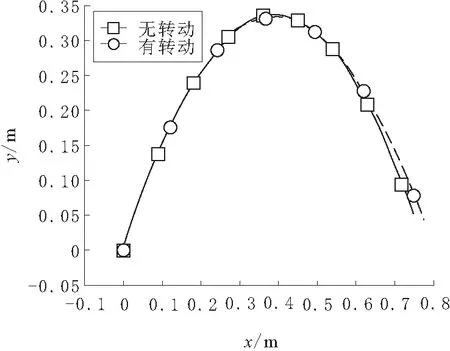
图5 有无旋转情况下的运动轨迹

通过图5可以发现，有转动的轨迹最大跳跃高度降低，但水平移动距离增加，这是因为在旋转情况下，机器人滞空过程中，垂直方向上获取的速度分量随角度变化逐渐减少，而水平分量相应增加。但角度变化对机器人滞空过程的轨迹形状整体影响并不大。

2.1.3 落地过程

因为该过程发生的是球体与地面的冲击，可以利用恢复系数[9]的方法对该情况进行分析。本文仅考虑跳跃机器人在滞空的过程中重力的作用，而忽略其他外部力(例如空气阻力)的影响。当地形不发生改变时，重力势能不变化，机器人落地时与起跳瞬间的动能不变。落地的碰撞会产生与地面垂直和平行2个方向上的速度变化，因为撞击瞬间很短且不考虑自身形变，水平方向上机器人不会发生滑动。假设垂直方向上的恢复系数为cver，而该系数满足0≤cver≤1。碰撞之后垂直速度vver1与碰撞之前垂直速度vver0满足

vver1=cvervver0

(17)

在水平速度上，满足公式

vhor1=vhor0-μ(vver0+vver1)=

vhor0-μ(1+cver)vver0

(18)

而碰撞之前的动能Tcollision为

(19)

可以得到撞击过程的动能损失为

(20)

该能量损失，适用于考虑机器人落地碰撞之后，二次弹起的情况，但这之后的分析不在本文的研究范围之内。

2.2 摩擦对跳跃过程的影响

机器人在跳跃时，弹簧的弹性势能转换为跳跃所需要的动能。提高弹性势能到动能的有效转换率是提升机器人跳跃能力的关键。

由受力分析已知，机器人跳跃过程中，受到的场力为重力，接触力为与地面的摩擦力，且仅仅只有跳跃支撑腿与地面接触所产生的摩擦力。摩擦力的影响主要发生在机器人跳跃支撑腿起跳开始阶段与地面撞击以及本体离开地面2个阶段，即图1b和图1c阶段。这2个阶段中，跳跃支撑腿与地面接触，并在弹簧的作用下与地面压紧，只有不发生打滑的情况下，弹簧的弹性势能才能传递给机器人本体用于跳跃，不会通过与地面的摩擦而被大量消耗。

为了保证跳跃支撑腿与地面接触过程中不打滑，摩擦力应大于起跳过程中水平力的分量，即

f=μkΔx·sinθ>kΔx·cosθ

(21)

其中Δx表示弹簧压缩量。从而得出不打滑的过程需要满足

(22)

分析跳跃过程会发现，跳跃过程开始，机器人本体会脱离地面，受到弹簧弹力和自身重力的同时作用，机器人本体的加速度方向并不是沿着弹簧方向，而是会偏向下，这就导致支撑腿与地面的夹角θ变小，有可能破坏发生支撑腿打滑的情况。假定打滑的边界摩擦角θi满足

(23)

当选取的地面摩擦因数为0.6时，依据机器人外壳框架结构，选取不发生结构干涉的起跳角度进行分析，这里选取摩擦角为59.0°，而2.1节计算的无滑动情况下夹角最终会降低到58.8°，小于边界摩擦角。在此,总结出起跳阶段产生打滑现象的情况：第1种情况，起跳之前，跳跃支撑腿与地面的夹角就小于摩擦角θi，导致支撑腿与地面接触瞬间就发生打滑；第2种情况，起跳过程中在重力作用下，θ逐渐减小，直至小于θi，开始发生打滑现象。

针对可能存在的打滑现象，依据现有的机器人模型和各部分参数情况，为确定起跳角度θ0，需要进行数值方式求解最终角度θk，当满足θk≥θi时，符合机器人起跳不打滑的设计要求。

3 跳跃机器人越障能力分析

3.1 障碍物的距离对越障的影响

分析跳跃机器人越障能力的评价标准，分为2种情况进行讨论:一种为翻越问题，机器人跳跃的运动轨迹与地面所围成的区域，可以完全包裹一个外形有限的障碍物，从而判断机器人能否顺利越过整个障碍，如图6所示；另一种为爬升问题，即机器人运动的预期目标是可以达到障碍物之上，该问题应用的场景往往出现在1次跳跃无法翻越障碍，需要连续多次向上攀爬的过程。也就是说跳跃的目的是达到目标高度即可。

如图6所示，分析翻越问题，为了简化分析计算过程，将机器人的运动过程简化为质点运动，但是在越障过程中机器人的外形是无法忽视的，在此将机器人的外形碰撞因素加入到障碍物上，即将障碍物的外形尺寸增加机器人的外形碰撞尺寸d。

图6 翻越问题示意

若起跳过程参数已知，轨迹抛物线为

(24)

当障碍物的外形方程满足yobstacle=f(x)，x∈(m,n)时，可以顺利越过的条件为

y≥yobstacle+bx∈(m-b,n+b)

(25)

假设翻越的障碍物为一个宽度为ly，高度为lx的长方形。设障碍物距离原点起跳点的距离为x1，则翻越需要满足的关系为

(26)

设上述2个不等式方程的结果为[λ1λ2]和[λ3λ4]，则最终可以翻越需要满足的关系为

x1∈[max{λ1λ3} min{λ2λ4}]

(27)

爬升问题相对于翻越问题，仅仅需要考虑更靠近起跳点的障碍物点A，利用上述同样的方法，得到的起跳距离x2满足的条件为

x2∈[λ1λ2]

(28)

3.2 起跳角度对越障的影响

当起跳阶段的起跳角度不同，导致θk和vk发生变化时，跳跃曲线随之发生变化，上述方程说明的越障问题依旧成立，但不同的跳跃曲线在面对相同的障碍物时，所表现出来的越障能力是不同的。如图7所示，很显然曲线i能更好地适应于翻越障碍物的情况。

图7 不同起跳角度的爬升问题

所以当机器人通过自身传感器或者其他方式获得了障碍物信息之后，需要规划机器人跳跃的初始角度。2.1节中较为详尽地考虑到整个起跳过程的动力学影响因素，为减少计算量，本文进行了如下简化：跳跃支撑腿的质量忽略不计，并在整个过程中不发生滑动摩擦；起跳过程中支撑腿与地面的夹角不会因为重力的因素发生变化，这是通过仿真观察，得出夹角变化量有限的情况下进行的假设；弹簧的弹性势能转化为机器人起跳之后的初始动能，转化的效率为ε。即弹簧的弹性势能以ε的效率转化为机器人跳跃的动能和势能，从而得到状态k时起跳角度与初始速度的公式满足

(M+m)g(rb-ri)sinθk

(29)

r0为弹簧的原长；rb为起跳之前最大压缩状态下弹簧的长度；ri为弹簧能够达到的最大伸长长度。可以得到vk与θk的关系满足

(30)

把式(30)代入式(24)中，就可以依据越障条件式(27)和式(28)，进行越障效果分析。

4 机器人起跳动力学仿真分析

为了继续探究起跳过程中，产生的打滑对跳跃机器人的影响，本节对球形跳跃机器人的起跳动力学进行了仿真分析。基于ADAMS软件，添加合适约束后的模型如图8所示。在结构绘制软件中建立机器人的模型并导入，通过定义材料、连接方式、驱动方式和接触方式等，搭建了该跳跃机器人的仿真平台。

图8 球形跳跃机器人仿真模型

仿真中，通过设置跳跃支撑杆与接触地面之间的摩擦因数，可以获得不同情况下机器人的运动状况，依据3.2节中总结的出现支撑腿滑动的情况，在仿真过程中，分别设置了0.2、0.5和0.7的摩擦系数。机器人在起跳角度为52.6°、与地面摩擦系数μ=0.5的情况下，可以观察到支撑腿末端有明显的向左滑移的过程，而μ=0.7的情况下没有滑动;在μ=0.2时，在接触瞬间支撑腿就开始滑动。首先，绘制跳跃过程的水平和竖直方向上的位移曲线，如图9所示。

图9 位移-时间曲线

由图9可以观察到，存在滑动最严重的μ=0.2的曲线，水平位移大大减少，而竖直方向上最高点的位移却有所增加，参照图10所示的速度-时间曲线，能够看出，跳跃过程中水平速度均保持不变，但是滑动导致水平速度的初始值大大减少，水平的位移减少。竖直方向上的加速过程3个曲线几乎一致，但是滑动时竖直最大速度稍有增加，原因是伴随着滑动过程的能量消耗，水平速度降低，但是水平方向动能不是100%消耗，因为在仿真以及实际情况下，受到地面、弹簧等的影响，部分动能转化到竖直方向，从而产生了竖直方向速度的变化。

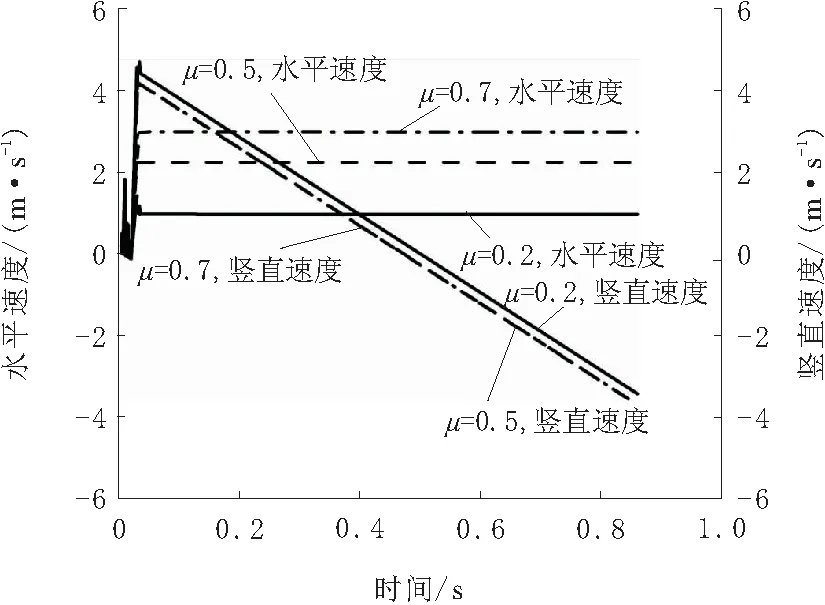
图10 速度-时间曲线

图11更详细展示了打滑情况对机器人动能、势能变化的影响。在摩擦系数不变时，动能随跳跃过程先减少后增加、势能先增加后减少，而随着摩擦系数的降低，相同时间情况下，动能减少，势能增加。机器人跳跃过程中总能量变化情况，如图12所示。

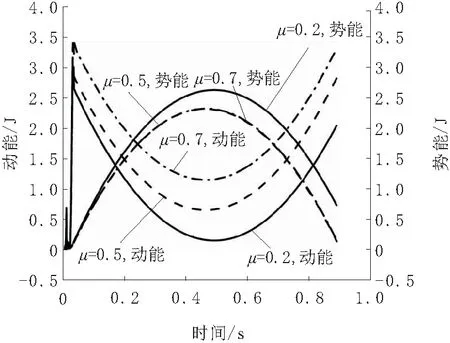
图11 动能势能-时间曲线

图12 总能量-时间曲线

由图12可知，动能和势能的变化趋势符合仅有重力作用下，机器人滞空过程中的能量转换过程，曲线初始阶段存在的能量跳变，是由仿真过程中弹簧的不确定因素导致的。总能量的曲线则更好地反映出存在滑动情况下，系统的能量有部分对外耗散掉了。此外，从图12中还可以得到，随着第1次跳跃过程的结束，时间在0.9 s时，机器人会发生2次弹起的情况，此时系统的机械能急剧减少，这部分能量的减少与机器人结构的力学性能和组成的材料性能有关，在仿真中并没有体现，会在以后的研究中继续探究。

5 结束语

本文基于一种可调节起跳角度的跳跃机器人，从机器人的整个跳跃过程出发，推导了任意起跳角度的跳跃过程动力学数值模型，并分析了不同摩擦存在的情况下对跳跃的影响，建立了相关的物理模型，通过仿真实验，验证了摩擦造成的跳跃机器人跳跃过程能量的损耗。该工作的开展有助于类似单足间歇跳跃机器人更好地规划自身的越障方案，对跳跃机器人的后期规划问题有着一定的帮助。