结合改进RBF与虚拟圆弧的船舶路径滑模控制
2021-03-02李宗宣卜仁祥章沪淦
李宗宣,卜仁祥, 章沪淦
(大连海事大学 航海学院, 辽宁 大连 116026)
欠驱动船舶路径跟踪是典型的运动控制问题,其主要目的是在不考虑时间限制的情况下,使船跟踪上参考路径[1]。为减化其控制难度,Fossen将line of sight(LOS) 制导技术引入到路径跟踪,将三维路径跟踪转化成了一维艏向控制[2]。但由于还存有速度不易测量、内部模型不确定以及环境干扰影响等问题,对其控制仍具有难度。对此,文献[3]设计线性观测器对船舶速度进行估计。为避免线性观测器易因估计偏差较大而使控制量振荡过大的问题,文献[4]提出一种非线性速度观测器。文献[5]也设计出非线性观测器,并同时对多艘船舶的速度进行估计。文献[6]采用径向基函数(radial basis function,RBF)神经网络观测器,对速度进行逼近。除了速度不易测问题,对外界干扰及模型不确定问题的处理也十分重要。文献[7]利用高增益观测器估计流干扰引起的时变漂角值。文献[8]结合LOS制导方法,提出RBF自适应算法。文献[9]设计自适应律分别对非线性水动力函数和外部扰动上界进行估计。文献[10-11]均利用自适应控制技术,解决外界环境干扰问题。文献[12]考虑到海流干扰,设计了结合LOS的滑模自适应控制器。文献[13]所设计的增量反馈滑模控制器,可通过积分环节以避免未知项问题。文献[14]在增量反馈的基础上,通过测量实际控制装置的抖振量和引入RBF技术,对滑模抖振问题进行了抑制。文献[15-16]分别利用最小学习参数和RBF技术避免模型未知项问题。文献[17-18]提出带辅助系统的滑模算法,并利用最小学习参数神经网络对不确定项进行逼近。文献[19]利用自适应和最小学习参数法解决外界干扰和内部不确定问题,并引入双曲正切函数设计滑模面,以减缓抖振。文献[20-21]为解决内部模型不确定和外部风流干扰,设计了以扩张状态观测器为核心的自抗扰控制器。除以上问题外,因为欠驱动船舶远洋航行主要是通过提前设计的定点,来设计参考路径[22],所以这容易使船在转向点(定点)处产生超调。为此,文献[23]提出预测位置方法,有效地提高了跟踪性能,但也减小了运算速度。文献[24]在传统LOS基础上根据路径偏差范围选择不同的参考艏向,并设计多倍船长的半径,使船在进入可接受圆内时提前进行转向。其方法简捷,却对不同转向角大小设计相同的可接受圆半径,缺乏船舶转向的灵活性。
考虑以上研究成果,本文利用双曲正切函数设计非线性观测器,实现对速度的估计,以解决速度值不易获取问题。通过RBF对模型不确定项和外界干扰逼近,以补偿艏向滑模控制器。而且在RBF中引入反正切函数进行权值更新,以提高逼近性能,防止因滑模面变化过大而导致逼近精度低或振荡的问题。并在转向点处设计根据转向角大小,而调节半径大小的虚拟圆弧路径,以提高跟踪性能。最终,对比仿真结果说明了所提控制算法在改进路径跟踪性能和RBF逼近未知项性能上的有效性。
1 船舶模型和控制目标
1.1 船舶运动模型
欠驱动船舶在水平面的位置及其运动参数如图1所示。其中,u是纵向速度,v是横向速度,φ是艏向角,U=(u2+v2)1/2是对地合速度,β=arctan(v/u)是漂角。本文以分离型模型(MMG)作为船舶运动模型及仿真被控系统,考虑风浪流干扰的MMG模型可表示为[25]

(1)
式中:m是船舶质量;mx和my是附加质量;IZZ是船绕竖直轴的惯性矩;JZZ是附加惯性矩;r是转艏角速度;φc和Vc分别是流干扰的方向和速度;XW,YW和NW为风干扰力矩;XWave,YWave和NWave为浪干扰力矩;XH,YH和NH是裸船体力矩;XP,YP和NP是螺旋桨力矩;XR,YR和NR是舵机力矩。MMG模型的输出是船舶位置(x,y,φ),控制输入是舵角δ,其隐含在舵机力矩(XR,YR,NR)的计算中,舵机力矩如下
(2)
式中:δ是舵角;tR是舵阻力减额份数;αH是船体附加横向力与舵横向力的比值;xH是船体横向力作用中心到船舶重心的距离;FN是舵正压力。
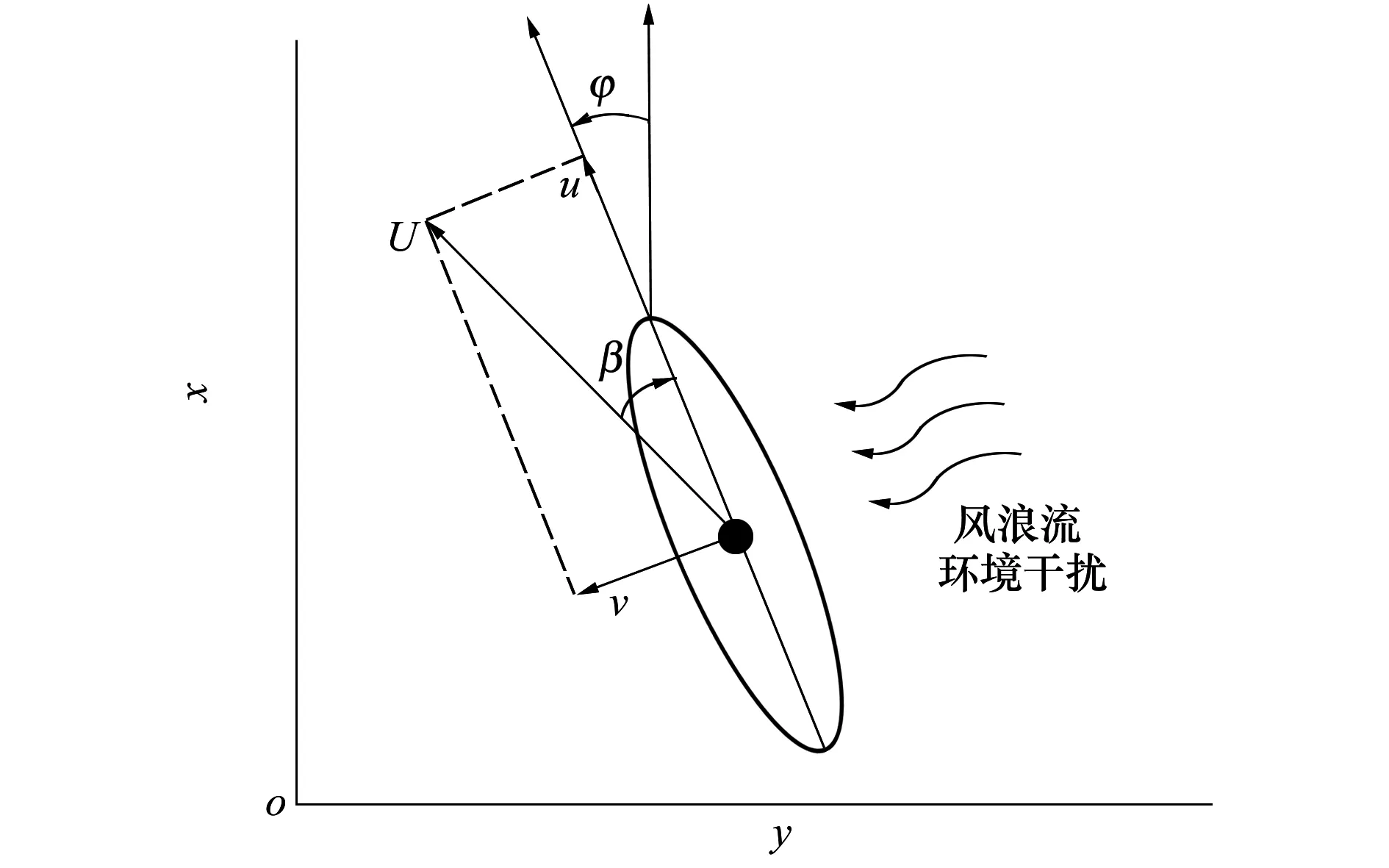
图1 船舶位置和运动参数
1.2 路径跟踪模型和控制目标
根据运动学和船舶Norrbin模型,建立如(3)式所示的船舶路径跟踪模型[25],用于设计路径跟踪控制器
(3)
式中:K是旋回性指数;T是追随性指数;a是正系数,f是包括内部模型不确定和外界环境干扰的总未知项。其中,船舶速度u,v及r,都不易直接测量。路径跟踪误差如图2所示。
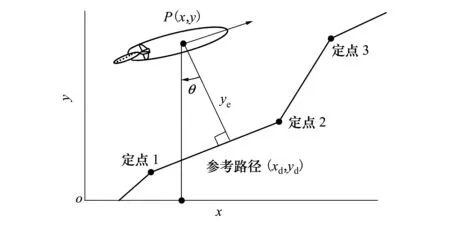
图2 路径跟踪误差
其中,ye是路径跟踪偏差,θ是参考路径角度。本文控制目标是通过路径跟踪模型(3)设计控制舵角δ,以使船跟踪上参考路径,即满足ye=0。所需假设条件如下
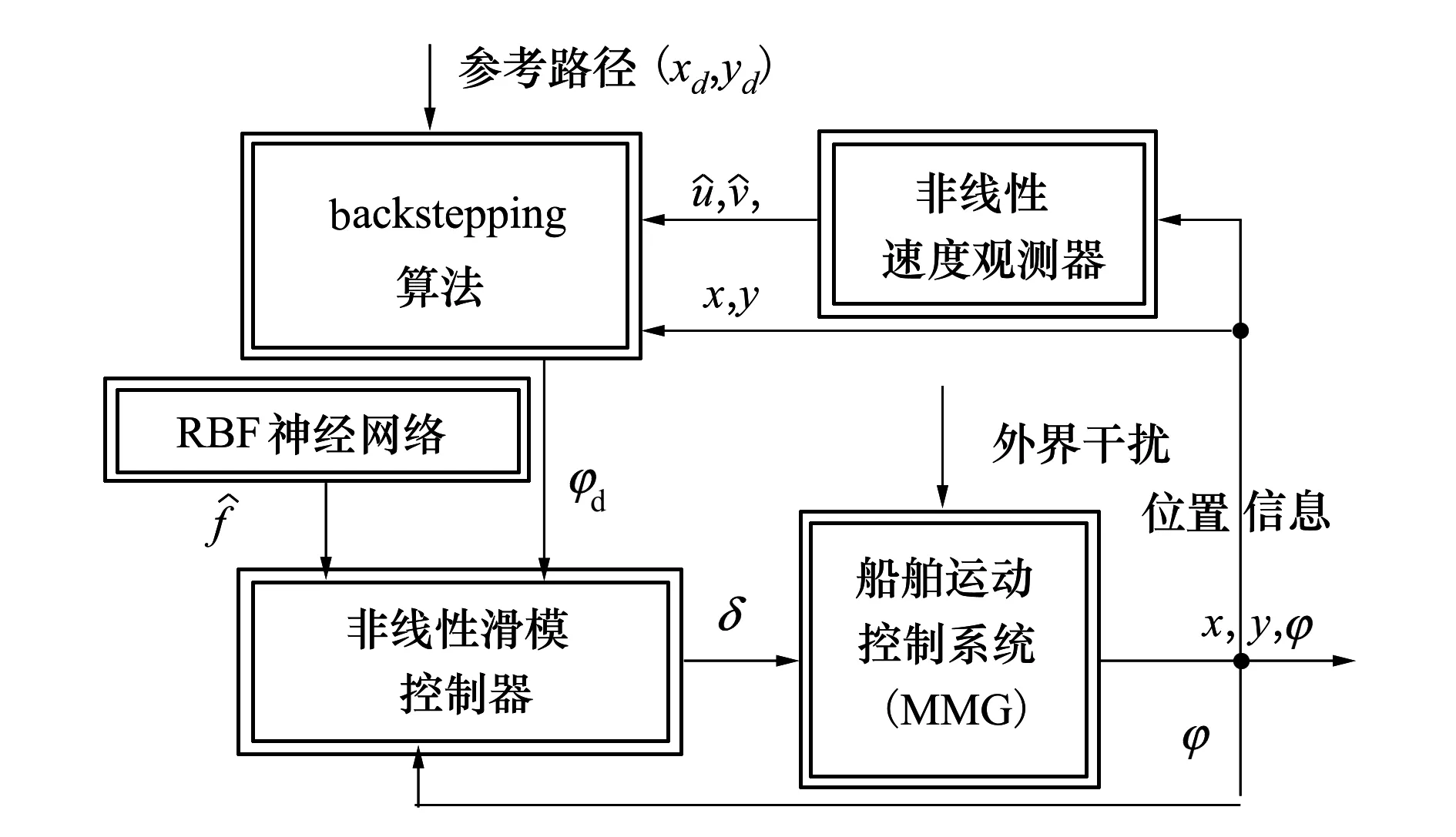
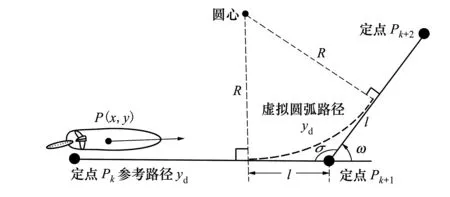
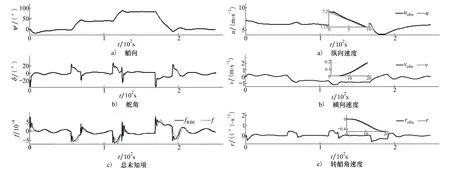
1) 总未知项f有界,即|f| 本文路径跟踪控制器由两部分组成,首先是基于backstepping方法的参考艏向角设计,其次是基于RBF滑模算法的艏向控制。控制器设计结构如图3所示。 图3 控制器设计结构 本节基于backstepping方法设计参考艏向角φd。 首先根据图2和点线距离公式,计算路径偏差如下 (4) 式中,A,B,C是参考路径参数。对(4)式求导有 (5) 为使(5)式和ye符号相反,设计参考艏向角如下 φd=-k0tanh(k1ye)-β+θ (6) 图4 虚拟圆弧路径 式中,k0和k1是正参数。而由于欠驱动船舶没有侧推器,并具有大惯性特点,所以当船已经运动到参考定点才开始转向时,将在转向点处产生较大超调。为避免此问题,本文在转向点处设计虚拟圆弧路径,如图4所示。其中:ω是船在转向点处的转向角;σ=π-ω是路径之间夹角;yd*是在路径衔接处所构建的虚拟圆弧路径,其与原路径yd相切;R是圆半径;l是船进入虚拟圆弧路径点到原跟踪定点之间的距离。由图可看出R=ltan(σ/2),R和l成同增同减关系,故本文通过设计l,以达到间接调节R的目的,即 (7) 式中:c1和c2是正参数;L是船长。半径R可根据转向角ω的大小来设计。即当ω较小时,将设计出较小的R,以保证船更接近定点;当ω较大时,对应较大R,以减小路径超调。 本节通过滑模算法对艏向φ进行控制,并利用RBF逼近总未知项f,进而补偿滑模控制器。根据非线性滑模和双曲正切函数设计滑模面[14] (8) 式中:k2和k3是正参数;φe=φ-φd是艏向跟踪误差。对s求导并代入(3)式 (9) 为使滑模面稳定,设计舵角如下 (10) (11) 式中:h是高斯函数的输出;W是理想权值;j代表隐含层第j个节点;x是RBF输入;c是中心点矢量值;b是宽度矢量值;ε是网络逼近误差,且可以限制得足够小。则f的估计值可表示为 (12) (13) 式中,η是正系数。对V求导如下 (14) 图5 函数对比 其中,考虑到反正切函数不仅严格有界,并且在定义域内的值变化更广,故本文利用反正切函数,设计估计权值如下 (15) 式中,k5和k6是正参数,k5用于压缩坐标,以避免因s过大而导致权值过大;k6用于提高s的增益,保证在s较小时,权值仍能有较大响应,从而提高逼近精度。 (16) (17) 本节对所设计的backstepping算法RBF滑模算法以及非线性观测器的稳定性进行分析。选择李雅普诺夫函数如下 (18) (19) 代入所设计的参考艏向、控制舵角和RBF估计权值,即(6)式,(10)式和(15)式有 (20) q+εs≤ζ (21) z1z2+z3≤μ (22) 根据(21)式和(22)式,则(20)式可表达为 (23) 则所提算法的稳定性可以被验证。 本节进行仿真实验,以大连海事大学育龙号实习船作为仿真对象,船长126 m,船宽20.6 m,满载吃水8 m,满载排水量14 635 t。以分离型船舶模型(1)作为仿真船舶运动模型,其中波浪和风干扰力计算与文献[25]相同。 仿真1为验证所设计控制器处理外界干扰、模型不确定和速度不可测等问题的能力,以及说明所提虚拟圆弧路径方法对路径跟踪性能提高的有效性,在此进行仿真实验。设计参考定点:P1(0,0),P2(4 000,0),P3(7 000,2 000),P4(8 000,6 000),P5(10 000,6 000)。船舶初始状态取为:(x,y,φ,u,v,r)=(0,300 m,0,7.2 m/s,0,0),即船到参考路径的初始偏差为300 m,初始速度为14.4 kn。外界干扰:风速10 m/s,时变风向30°sin(0.02t),流速1.0 m/s),时变流向10°sin(0.005t),波浪遭遇角φ-30°sin(0.02t),浪波长83 m,浪高3 m。 图6 路径跟踪 图7 圆弧半径 图8 艏向、舵角和总未知项 图9 纵向速度、横向速度和转艏角速度 图6至9为仿真结果。图6中,yd是参考路径,y3是文献[24]所用设计定常倍船长的可接受半径,以进行定点提前切换的结果,yR1和yR2是所提构造虚拟圆弧的路径跟踪结果,其中yR1是根据转向角ω大小设计可变圆弧半径,即在(7)式中取l=L(5.5-2.5cosω)计算半径R1,而yR2是取常数l=4L计算R2。可以看到,在存有外界干扰和模型不确定的情况下,3种方案均能使船准确地跟踪上参考路径。而yR1可在转向角较小的P2点处更接近路径,在转向角较大的P4处减小超调,说明所提可变半径圆弧方案,能够提高路径跟踪性能。图7可看出当转向角ω较小时,如ω2(34°)和ω3(43°),R1将比R2更小,以使船更接近定点;当ω较大时,如ω4(76°),R1将比R2更大,以减小超调。图8a)和8b)描述了艏向φ和舵角δ的变化,由于时变干扰影响,φ和δ保持着一定的角度以抵抗扰动。在船开始转向时,因为艏向将有较大变化,所以δ变化也较明显。图8c)展示了所采用的RBF对总未知项f的逼近效果,其可以成功地逼近f。图9说明了所建立非线性观测器的性能,在大约10~20 s时,便可准确地估计出速度u,v和r。 仿真2为验证在RBF中引入反正切函数进行权值更新,以提高逼近未知项性能的有效性,在此基于本文所提RBF权值更新律与文献[16]中线性更新律,分别设计RBF滑模控制器,并加入跳变的时变干扰,进行对比仿真。外界干扰:①t≤500 s时,风速5 m/s,流速0.3 m/s;②500 s 图10 不同RBF的路径跟踪 图10至11为仿真结果。图10中,yNRBF是基于本文所提非线性权值更新方法的路径跟踪结果,yLRBF是线性权值更新的结果,yd是参考路径。可看到yNRBF和yLRBF都能跟踪上参考路径,由于跳变时变干扰的影响,在(3 200 m,0)附近,产生不到5 m的波动,但很快趋于稳定,收敛在船宽的1/10以内,即不到2 m,这符合实际航行情况,其中yNRBF的波动幅度较小一些。图11a)描述了所提RBF神经网络估计总未知项f的结果。在50 s左右,fNRBF便能成功地逼近f。图11b)展示了RBF逼近误差fe的对比结果,其中,feNRBF和feLRBF分别是基于反正切函数和线性函数的逼近误差。可以看出在突变干扰产生时(t=500 s/1 000 s附近),feNRBF的变化幅度更小,收敛速度也较快。说明所提权值更新法,可提高RBF对f的逼近性能。 图11 总未知项和逼近误差 本文通过backstepping法将欠驱动船舶路径跟踪转换为艏向控制,其次设计RBF神经网络滑模控制器,以对艏向进行控制。其中,基于双曲正切函数建立速度观测器,以解决速度不易获取问题。此外,构建根据转向角来调节半径的圆弧路径,以提高路径跟踪性能。并引入反正切函数对RBF权值进行更新,以提高对模型总未知项的逼近性能。最终对比实验表明:不需速度的测量,控制器仍能使船在风浪流时变干扰下准确地跟踪上参考路径。既减小了路径超调,又尽可能地逼近参考定点,且提高了对未知项的逼近精度。说明了控制器解决速度不易测﹑外部干扰和内部不确定的能力,以及改进路径跟踪和RBF逼近性能的有效性。下一步研究将考虑以螺旋桨和舵角为多控制输入的船舶轨迹跟踪控制。
2 路径跟踪控制器
2.1 backstepping算法
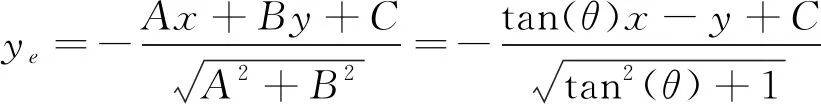
2.2 RBF滑模控制器
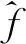

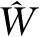


2.3 非线性观测器
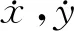


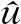
2.4 稳定性分析



3 仿真分析



4 结 论
