基于BP人工神经网络喷射成形7055铝合金的本构模型

2021-03-02崔树刚周皓天周易名张肖佩佩程晓农

航空材料学报 2021年1期

罗锐, 曹赟, 邱宇, 崔树刚, 周皓天, 周易名,袁飞, 张肖佩佩, 程晓农*

（1.江苏大学材料科学与工程学院，江苏镇江 212013；2.中国航空制造技术研究院，北京 100024）

7055铝合金属于超硬Al-Zn-Mg-Cu系变形铝合金[1]，该合金具有优异的综合力学性能，目前已被广泛应用于航空航天领域飞行器部件的制造当中，例如空客A380大飞机的压力舱桁条与上机翼桁条均采用7055铝合金[2-4]。但是在整个零部件制造流程中，传统铸造工艺带来的成分偏析容易使合金发生热裂失效，很难满足高标准航空航天部件的服役要求[5-6]。而喷射成形是一种“近终形”成形技术，利用合金雾化快速沉积凝固的方式，大幅提高合金元素的固溶程度且晶粒组织均匀细小，有助于后续热加工环节的进行[7]。在热加工制造环节中，喷射成形7055铝合金还需要进行热挤压、锻造等多道热加工工序，不当的热加工工艺易引发合金的开裂失效。高温流变应力曲线能够综合反映各热加工工艺参数与合金组织演变之间的内在联系，因此研究该材料的高温变形行为具有重要的工程意义。

揭示合金在热加工过程中的变形规律及其本构关系是研究其高温变形行为的基础。科研人员通常采用传统唯象型Arrhenius本构模型建立材料的本构关系，然而合金的变形过程受到多方面因素的共同影响，致使流变应力与各加工参数之间呈现出复杂的非线性关系，基于回归算法的传统Arrhenius型本构方程常难以保证流变应力值的精准预测[8]。例如Wu等[9]和Wang等[10]分别利用传统唯象型Arrhenius本构模型研究2024A铝合金与2219铝合金的流变应力情况，预测值的平均相对误差值高达5.02%和3.11%。随着计算机技术的不断发展，近年来迅速成熟的基于BP人工神经网络的本构模型依靠其自组织、自修正以及内插、外插的技术特点能够有效得耦合多元变量、解决非线性问题并大幅提高模型准确度[11]。Wang等[12]利用该模型预测Al-Zn-Mg-Sc-Zr合金的流变应力情况，其相关系数高达0.9984，而Arrhenius本构模型的相关系数仅为0.9887。对于航空航天用喷射成形7055铝合金来说，构建材料的本构模型并精确预测其加工过程中的流变应力演变规律迫在眉睫。

通过先进的Gleeble热力模拟技术对喷射成形7055铝合金（挤压态）进行等温热压缩实验，获取该合金的高温流变应力曲线，并依据曲线数据分别构建该合金的传统唯象型Arrhenius本构方程以及BP神经网络型本构方程。通过流变应力预测值的对比，分析该两种模型的精准程度，并为工业生产中热加工参数的制定提供理论指导。

1 实验及方法

本实验所涉及的喷射成形7055铝合金（挤压态），其化学成分如表1所示。将合金加工成φ10 mm × 15 mm的圆棒状试样，并利用Gleeble-3500型热力模拟试验机对其进行等温热压缩实验。压缩前，在试样两端粘贴石墨片以起到润滑以及防止鼓肚效应的作用。将试样加热至变形温度（350 ℃、375 ℃、400 ℃、425 ℃、450 ℃），保温30 s后进行不同应变速率下（1 s-1、5 s-1、10 s-1、20 s-1）的热压缩，其热变形工艺如图1所示。压缩完成后立即淬火冷却至室温。将实验获取的热压缩数据进行图像化处理，获得流变应力曲线并进行后续研究。

表 1 实验用喷射成形7055铝合金的化学成分（质量分数/%）Table 1 Chemical composition of experimental 7055 aluminum alloy（mass fraction/%）

图 1 热变形工艺流程Fig. 1 Hot deformation process flow diagram

2 结果与讨论

2.1 材料应力-应变曲线

如图2所示，根据实验所得热压缩数据，获得7055铝合金的流变应力曲线。由图2可得，形变初期，流变应力值随应变量的增加而急剧上升。这是由于形变初期，合金内部的位错迅速纠缠、增殖，位错密度大幅上升造成材料发生加工硬化现象[13]。随着应变量的进一步增加，可动位错数量上升，且由于该合金较高的层错能，扩展位错易发生束集、交滑移，有效起到动态软化的作用[14]。当加工硬化与动态软化达到平衡状态时，流变应力曲线呈现出稳态平台且具有动态回复特征。综合对比图2（a）、（b）与图2（c）、（d）可知该合金的流变应力对于变形温度（T）与应变速率（ε˙）较为敏感。其流变应力值与变形温度（T）呈现出负相关，而与应变速率（ε˙）呈现出正相关。

2.2 唯象型Arrhenius本构方程

唯象型Arrhenius 本构方程是当下广泛运用的流变应力预测模型。该模型是由Sellars等[15-16]学者提出的。

本文利用该模型对应变量为0.15的7055铝合金进行Arrhenius本构方程研究，其相应的拟合过程如图3（a）～（d）所示。通过斜率以及截距的运算处理，得到各材料常数分别为n1= 7.7406；β=0.0791；α=β/n1= 0.0102；n= 6.1473。同时，热变形激活能Q的计算值为76.6704 kJ•mol-1，处于较低水平，显示该合金具有较好的热加工成形性能。

Zener-Hollomon指数（Z）与合金的动态软化程度具有一定相关性[17]。其公式如式（1）所示。对该公式进行对数运算得到式（2）。

故该喷射成形7055铝合金在应变量为0.15时的Arrhenius型本构方程可表示为：

然而合金的流变应力与各变形参数间并非简单的线性回归关系，上述本构方程算法缺乏对应变量等其他因素影响的考量。故下文将在上述研究的基础上耦合应变量因素，以使得本构方程能够更加精准地预测合金的流变应力状态。

图 2 喷射成形7055铝合金不同参数下的流变应力曲线Fig. 2 Flow stress curves of spray forming 7055 aluminum alloy with various deformation parameters（a）350 ℃；（b）425 ℃；（c）1 s-1；（d）5 s-1

图 3 喷射成形7055铝合金不同本构参数关系曲线（应变量0.15）Fig. 3 Relationship curve of various constitutive parameters of spray forming 7055 aluminum alloy（strain 0.15）（a）lnε˙-lnσ ；（b）lnε˙-σ ；（c）lnε˙-l n(sinh(ασ))；（d）-l n(sinh(ασ))；（e）l n(sinh(ασ))-lnZ

基于耦合精度以及计算负荷的综合考虑，本研究中将从应变量0.05～0.7的流变数据中每间隔0.025的应变量取一参数点，并对各应变量参数下的材料参数值进行6次多项式拟合，拟合图像如图4所示。从图4中可得，各参数的拟合相关度较为良好。α以及n值在应变量为0.2左右处出现一极小值，而Q与lnA值则在应变量0.3之后几乎保持一水平线。表明该合金在0.3以下的较小变形量下，其塑性加工性能变化浮动较大，而0.3以上的较大变形量状态下塑性加工性较为稳定。各材料常数与应变量的数据关系详见表2。

图 4 不同本构常数与应变量之间的关系Fig. 4 Relationship between various constitutive constant and ture strain （a）α-ε；（b）n-ε；（c）Q-ε；（d）lnA-ε；

表 2 材料常数与应变量关系数据表Table 2 Relationship between material constant and true strain

通过上述耦合应变量处理后的本构方程模型，再代入相应的T、、ε值，即可获得该合金在不同变形条件下的流变应力预测数值。其预测数值与实验数值对比图象如图5所示。图象整体呈现出较高的预测正确性。然而在高应变速率如图5（b）中的425 ℃，20 s-1下预测值偏低，在图5（c）中的1 s-1的应变速率下，变形初始阶段红圈所指处预测精确率浮动较大。这是由Arrhenius本构方程的固有数理模型缺陷所造成的，使得非线性预测无法达到更高的精度值。

图 5 不同变形参数下Arrhenius本构方程预测结果Fig. 5 Prediction results of Arrhenius constitutive equation with various deformation parameters（a）350 ℃；（b）425 ℃；（c）1 s-1；（d）5 s-1；

2.3 BP人工神经网络型本构模型

BP人工神经网络（BP-ANN）是当下计算机科学领域所流行的算法之一。将BP-ANN模型应用于合金本构方程的构建，利用其误差反馈自修正的特点能够有效提高非线性流变应力预测的准确性[18]。BP-ANN由输入层、隐含层以及输出层这三个部分构成，其模型结构图如图6所示。在输入层部分，需插入三个神经元节点：T、、ε。输入层数据经函数传递至隐含层后，隐含层对其进行网络化计算，最终通过函数传递至输出层，得到流变应力σ数值。若在输出层得不到精准预测的结果，则该模型会进行反向传播，将误差信号沿着各神经元节点返回传递[19]。其间各神经元权值将受到修改，经过不断迭代，最终达到理想精度的信号输出，即训练过程结束。

研究表明，隐含层的节点数表示该网络的数据处理能力。节点数的多少决定该模型反馈算法的准确程度[20]。本研究中对隐含层节数为8～20的情况均作出尝试，发现对于该合金，节点数的多少对于预测准确度来说影响不大。故综合考虑模型预测准确度与计算机计算能力，将隐含层节点数定为15个，即采用3 × 15 × 1的网络结构。

此外T、、ε数量级相差较大，若以原数值输入网络模型，必然会削弱小数量级参数、ε在模型运算中的权值，影响到模型的收敛速度和预测精度[21]。故在进行运算前，需对上述参量进行归一化处理，本工作采用mapminmax算法，其公式如式（4）所示。

式中：y为归一化后的T、、ε参数值；x代表各T、、ε参数值；而xmin为参数的最小值；xmax为参数的最大值。通过该式可使得参量初始值控制其范围在0.1～0.9之内。而后利用MATLAB软件完成上述模型的构建，其中两次传递过程分别通过Tansig函数和Purelin函数实现，训练函数为Trainlm，目标精度设为10-5，网络学习率设为10-4。

图 6 神经网络模型结构图Fig. 6 Structure diagram of neural network model

图7为BP-ANN模型的流变应力预测结果，由图7可以看出，红圈标记部分显示在变形初始阶段预测值略微偏离实际实验值，这是由于该模型采用固定应变步长所造成的。在加工硬化阶段，应力数据点密集，采取更小的步长能够增加该阶段的预测准确率。在初始形变阶段后，流变应力预测在稳态应力阶段均显现出超高的预测准确性。

图 7 不同变形参数下BP神经网络本构方程预测结果Fig. 7 Prediction results of neural network constitutive equation with various deformation parameters（a）350 ℃；（b）425 ℃；（c）1 s-1；（d）5 s-1；

2.4 本构模型预测对比

对于Arrhenius模型与BP-ANN模型，本文利用通用平均相对误差δ与相关性系数R2对模型精度进行对比。其计算公式分别如式（5）、（6）所示。

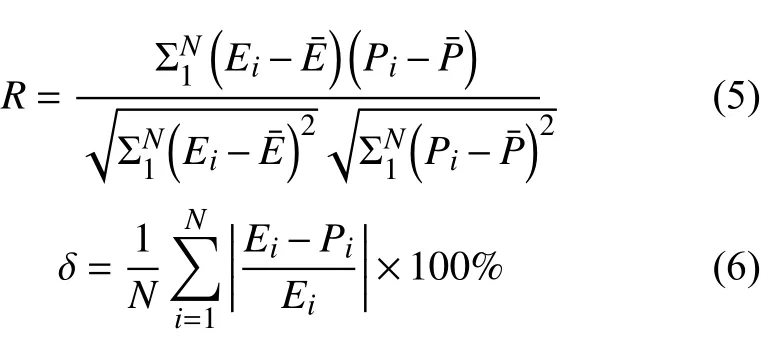
式中：Ei为实验流变应力值，为其平均值；Pi为模型预测流变应力，为其平均值；N为数据总量。

图8显示该两种模型的整体预测精度对比。图8所示，BP-ANN模型数据点更加集中，具有更好的预测准确性，其平均相对误差δ仅为0.813%。而Arrhenius模型的δ值大于2%，相关系数R2对比同样显示BP-ANN模型具有更高的精度。从图9的残差分析中不难发现，两种模型在中等应变量0.3～0.5附近时，均具有极高的预测准确度，在此范围以外均有不同程度的浮动。BP-ANN模型的残差保持在 ± 4.5 MPa以内，而Arrhenius模型浮动较大，在[-8，-4.5]区间内亦存在较多数据点，预测精度相对较差。

图 8 不同模型预测应力值的相对误差与相关性系数对比Fig. 8 Comparison of relative errors and correlation coefficients of prediction stress by different models（a）Arrhenius model；（b）BP-ANN model

图 9 唯象型Arrhenius本构模型与BP神经网络模型残差对比Fig. 9 Comparison of residual between phenomenological Arrhenius model and BP neural network model

图10显示两种模型平均绝对误差和平均相对误差的对比状况。如图所示，BP-ANN模型在不同温度下预测准确度变化较小，稳定性良好。其平均绝对误差均保持在1.2 MPa的低水平，而平均绝对误差保持在0.7%～1.05%范围内。Arrhenius模型的平均绝对误差在375 ℃时出现极小值，在450 ℃时出现最大值，且平均相对误差在1.4%～3.5%的较大范围内浮动。随着温度升高，该模型的预测精度总体呈现出下降趋势。值得注意的是，7系铝合金的热加工温度范围一般在450 ℃左右，该温度下强化相状态将会发生较大改变，MgZn2相易回溶于α-Al基体当中，降低晶界强度，造成沿晶开裂，削弱了合金的可加工性能[22-23]。BP-ANN模型通过反馈传递使得本构方程预测在该温度区间保持较高的准确性。而唯象型Arrhenius本构模型预测的精确度对温度变化适应性较小，且在450 ℃下相对误差达到峰值，较难准确预测合金高温加工性能。综上所述，对于航空航天用喷射成形7055铝合金而言，BP-ANN本构模型更能有效描述合金在高温变形条件下的流变行为。