用焦利秤测量液体表面张力系数
2021-03-01王雅红赵鹏程张丁立林芃杉PascalineUMUHIRETandongChristerbelBIN
王雅红,潘 政,赵鹏程,张丁立,李 维,乔 月,林芃杉 ,Pascaline UMUHIRE,Tandong Christerbel BIN
(1.大连工业大学 基础教学部,辽宁 大连 116034;2.大连工业大学 轻工与化学工程学院,辽宁 大连 116034;3.大连工业大学 机械工程与自动化学院,辽宁 大连 116034;4.大连工业大学 国际教育学院,辽宁 大连 116034)
0 引 言
液体表面张力是由于液体表面层内液体分子受力不平衡引起的,液体表面层内分子受到了一个指向液体内部的合引力作用,使得液体表面具有自动收缩的趋势。因此液体表面就像一张被绷紧了的橡皮膜,使得表面层内不同部分之间有张力存在,这种张力就称为液体表面张力[1]。液体表面张力是表征液体性质的一个重要参数,可用液体表面张力系数来描述[2]。几乎所有的工农业生产和日常生活都与表面张力原理有直接或间接关系,如喷洒农药、涂抹涂料、洗澡、刷牙、洗衣都与表面张力有关。
测量液体表面张力系数常用方法有毛细管法[3]、悬滴法[4]、最大气泡压力法[5]和拉脱法[6-7]等。其中,拉脱法具有方便快捷、操作简单的特点,是目前常用的一种测量液体表面张力系数的方法。影响表面张力系数测量结果的因素很多,比如水膜质量和金属丝浮力,弹簧弹性系数及弹簧质量等,但常规的测量方法中没有考虑这些因素对测量结果的影响[8-11]。文献[12]认为,水膜质量可以忽略,金属丝浮力对表面张力系数测量结果的影响不能忽略,但文中没有定量分析水膜重力及金属丝浮力对测量结果的影响是否显著,是否具有统计学意义。
本测量方法利用焦利秤,基于拉脱法,用不同形状的弹簧测量纯净水在20 ℃时的表面张力系数,探索水膜质量、金属丝浮力、弹簧质量、弹簧形状及弹簧弹性系数对液体表面张力系数测量结果的影响,提出一种非理想弹簧等效弹性系数测量方法,并通过实验数据分析了其合理性。
1 拉脱法测量表面张力系数原理
液体表层内分子力的宏观表现,使液面具有收缩的趋势。想象在液面上画一条线,表面张力就表现为直线两侧的液体以一定的拉力相互作用。这种张力垂直于该直线且与线的长度成正比,比例系数称为表面张力系数。测量装置如图1所示。图1(a)为使用焦利秤的拉脱法测量液体表面张力系数原理图;图1(b)为П型金属丝紧贴液面时的放大图。此时,金属丝受到3个力的作用,即弹簧竖直向上的拉力F1,金属丝重力G1,金属丝向上的浮力FB1,当系统达到平衡时,有

图1 测量装置图Fig.1 Diagram of measuring instrument
F1+FB1=G1
(1)
图1(c)是金属丝拉出水面后形成的液膜破裂前的放大图,金属丝及液膜受到5个力的作用,即弹簧竖直向上的拉力F2,金属丝重力G1,水膜重力G2,金属丝向上的浮力FB2,液体表面张力T。当系统达到平衡时,有
F2+FB2=T+G1+G2
(2)
由式(1)、(2)可得
T=F-G2-FB
(3)
式中:FB为图1(c)中露出液面的金属丝在图1(b)中所受的浮力。
T=2α(l+d)≈2αl
(4)
F=F2-F1=kΔy
(5)
式中:α为该液体表面张力系数,l为П形金属丝两脚间距离,d为金属丝直径,k为弹簧弹性系数,Δy为液膜形成前至液膜破裂时弹簧伸长量。
G2=ldhρg
(6)
式中:h为液膜高度,ρ为被测液体质量密度,g为重力加速度。
FB=FB1-FB2=π(d/2)2(2h+l)ρg
(7)
由式(3)~(7)可得
(8)
式(8)即为利用拉脱法测定液体表面张力系数公式,待测量有k、l、d、Δy和h。
因为液膜质量及金属丝浮力远小于弹簧弹力,所以实际测量时往往忽略这两项,表面张力系数简化为
(9)
2 非理想弹簧等效弹性系数定义
2.1 非理想弹簧等效质量及等效弹性系数
拉脱法测量液体表面张力系数,首先要测量焦利秤所配弹簧弹性系数,常规方法是将弹簧竖直放置,然后在弹簧末端挂上质量为m砝码,测量弹簧的伸长量Δy,根据胡克定律,弹簧弹性系数为
(10)
这种测量方法是将弹簧视为理想弹簧,不计弹簧质量,认为弹簧是均匀伸长的。但实际应用的弹簧都是有质量的非理想弹簧,竖直放置时,由于自身重力作用,弹簧是非均伸长的,尤其对于圆柱形弹簧,竖直放置时,由于重力作用,弹簧上端的变形程度大于下端。基于这种常规方法测量的弹性系数值要小于其真实值,根据式(8)或式(9),这种常规方法测量的表面张力系数将偏离真实值。文献[13]和[14]分别讨论了竖直放置的圆柱形弹簧和圆锥形弹簧的等效质量。设弹簧质量为M,等效质量为μ,则
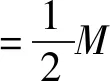
(11)
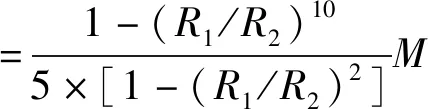
(12)
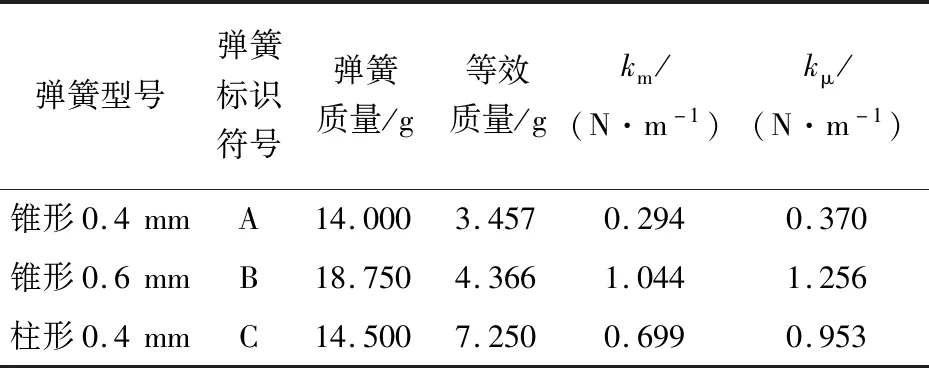
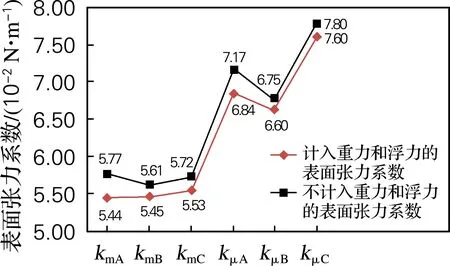
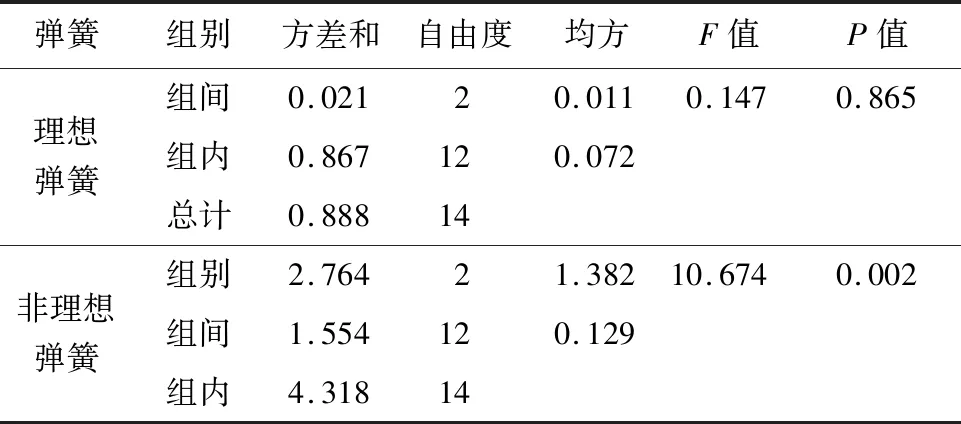
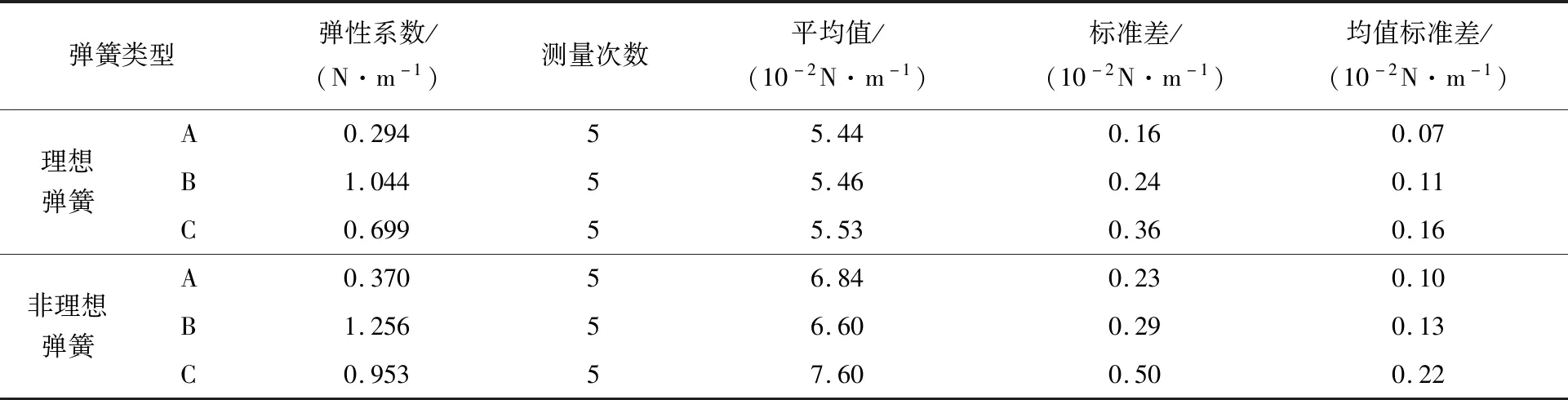
式中:R1和R2分别是圆锥形弹簧的上、下半径,R1 进一步假设因等效质量引起的重力作用在弹簧质心上,弹簧竖直放置时,由于自身重力作用,弹簧将伸长,设质心的移动距离ΔYC,定义非理想弹簧等效弹性系数为 (13) 如果已知弹簧的等效质量和由自身重力引起的质心移动距离,可由式(13)计算非理想弹簧等效弹性系数。 设一质量为M,质量沿弹簧长度方向均匀分布的非理想弹簧,现将该弹簧等分成n段,每段看成劲度系数为k,质量为m的小弹簧,该均质弹簧则由n个劲度系数为k,质量为m的小弹簧串联而成。当其竖直悬挂时,从上至下各小弹簧的伸长量分别Δy1,Δy2,…,Δyn,其中,质心所在处的伸长量为Δyn/2。因为每个小弹簧受到弹簧自重引起的向下拉力不同,故有 (14) (15) 设ΔYC=Δy1+Δy1+…+Δy1/2,ΔYC即为质心处的移动距离,代入上式得 (16) 同理,将式(16)第1项至第n项相加得 (17) 其中,ΔY=Δy1+Δy1+…+Δyn为弹簧底端移动距离,即弹簧总伸长量。 当n→∞时,有 (18) 图2为焦利秤所配备的圆锥形弹簧剖面图,上下圆周半径分别为R1和R2,弹簧竖直放置时,其自然长度为L,C点为弹簧质心的位置,距离上端的距离为YC。如果沿着弹簧母线的方向单位长度的匝数相同,则圆锥形弹簧可以等效为一个匀质分布的圆台侧面,其质心的位置为 图2 圆锥形弹簧截面图Fig.2 Diagram of conical spring section (19) 根据文献[15],一条长为l、半径为r的金属丝紧密缠绕成匝数为N、圆周半径为R的圆柱形弹簧,均匀伸长时弹簧的劲度系数为 (20) 其中G为金属丝剪切弹性模量。因此,当匝数相同时,弹簧圆周半径越小,弹性系数越大。假设圆锥形弹簧是由无数个匝数相同的小圆柱形弹簧串联而成,当其竖直放置静止时,从下至上,小弹簧的弹性系数逐渐增大,但每个小弹簧受到的向下的重力逐渐增大,所以,可以粗略地假设每个小弹簧的伸长量相同。由(19)式可知,其质心的移动距离为 (21) 式中:ΔL为圆锥形弹簧竖直放置时,由弹簧自重引起的弹簧总伸长量。 实验采用拉脱法,选用焦利秤测量弹簧的弹性系数及纯净水在20 ℃时的表面张力系数。 焦利秤配备3种弹簧,分别用A、B、C来表示,其中A和B分别是金属丝直径为0.4和0.6 mm 的圆锥形弹簧,C是金属丝直径为0.4 mm 的圆柱形弹簧。用kmA、kmB、kmC标识常规方法测得的理想弹簧弹性系数,用kμA、kμB、kμC标识非理想弹簧等效弹性系数,表1是弹簧弹性系数的测量结果。由表1可知,对于每种型号的弹簧,其等效弹性系数均大于将其视为理想弹簧时测得的弹性系数。无论是理想弹簧还是非理想弹簧,A弹簧的弹性系数都是最小的,分别为kmA=0.294 N/m和kμA=0.370 N/m;B弹簧的弹性系数最大,分别为kmB=1.044 N/m和kμB=1.256 N/m;C弹簧的弹性系数介于两者之间,分别为kmC=0.699 N/m和kμC=0.953 N/m。 表1 不同弹簧弹性系数测量结果Tab.1 Measurement results of the force constant of different springs 用不同型号弹簧测量表面张力系数,各测量5次,分别用理想弹簧弹性系数和非理想弹簧弹性系数计算计入水膜重力和金属丝浮力前后液体表面张力系数,测量的平均值见图3。由图3可知,同一个弹簧,无论将其视为理想弹簧还是非理想弹簧,计入水膜重力及金属丝浮力前后,表面张力系数测量结果不同,修正前的表面张力系数均值大于修正后的均值;表2是3种弹簧测量平均值统计描述,3个理想弹簧测得修正前后表面张力系数平均值分别是5.70×10-2和5.48×10-2N/m,修正前后均值差为2.2×10-3N/m;如果将弹簧视为非理想弹簧,则修正前后测量结果分别是7.24×10-2和7.01×10-2N/m,修正前后均值差为2.3×10-3N/m。 表2 计入重力及浮力前后水的表面张力系数平均值统计描述Tab.2 The statistical description of the mean value of water surface tension coefficient before and after taking into account of the gravity on the water film and the buoyancy on the metal wire 图3 计入水膜重力及金属丝浮力前后液体表面张力系数Fig.3 Liquid surface tension coefficients before and after taking into account of water film gravity and wire buoyancy 表3是独立样本t检验的结果,检验计入重力及浮力前后液体表面张力系数的差异是否显著,是否具有统计学意义。由表3可以看出,对于理想弹簧和非理想弹簧,Levene方差齐次性检验的显著性P值均大于0.05,说明表面张力系数测量结果具有方差齐次性,应该选择方差齐次性的t检验结果,即t=2.399(理想弹簧)和t=1.104(非理想弹簧),相应的t检验显著性分别为P=0.023(<0.05)和P=0.279(>0.05)。所以,用理想弹簧测得的表面张力系数,计入重力及浮力前后表面张力系数测量结果差异显著,这种差异具有统计学意义,不能忽略其对测量结果的影响;但对于非理想弹簧,这种差异没有统计学意义,可以忽略水膜重力及金属丝浮力对表面张力系数测量结果的影响。 表3 计入重力及浮力前后液体表面张力系数独立样本t检验Tab.3 Independent sample t test of liquid surface tension coefficient before and after considering buoyancy and gravity 3.3.1 测量结果单因素方差分析 由图2可知,不同弹簧测量结果不同,将同一个弹簧视为理想弹簧和非理想弹簧,测量结果也不相同。由表4弹簧对液体表面张力系数影响可知,若将不同弹簧均视为理想弹簧,测量结果差异显著性P值为0.865,大于0.05,说明如果不考虑弹簧质量,不同型号弹簧测量结果差别不显著;但如果将弹簧视为非理想弹簧,差异显著性P值为0.002,远小于0.05,说明不同型号的非理想弹簧的测量结果差异显著。 表4 弹簧对液体表面张力系数影响的单因素方差分析Tab.4 One-way ANOVA for the influence of different springs on liquid surface tension coefficient 表5是单因素方差分析多重比较结果,分析理想弹簧和非理想弹簧测量结果差异显著性。由表5可知,对于每一类型的弹簧,视为理想弹簧的测量结果均小于相应的非理想弹簧测量结果,且差异显著性P=0(<0.05),所以这种差异具有显著的统计学意义,说明弹簧质量对测量结果的影响显著,不能忽略弹簧质量对测量结果的影响。 表5 理想弹簧和非理想弹簧测量液体表面张力系数结果比较Tab.5 Comparison between the surface tension coefficients measured by ideal springs and non-ideal springs 3.3.2 测量结果与标准值差异显著性分析 表6是单样本t检验结果,分析不同型号弹簧测得的表面张力系数与标准值之间差异的显著性。纯净水在20 ℃时的表面张力系数标准值约为7.28×10-2N/m[16-17],如果测量结果与标准值相差越小,则说明测量结果越准确。根据纯净水表面张力系数测量值与标准值可知(表6),对于每一类型的弹簧,将其视为理想弹簧的测量结果均小于标准值,而且与标准值的差异显著性P=0(<0.05),说明这种差异具有明显的统计学意义;若将弹簧视为非理想弹簧,其测量结果比视为理想弹簧的测量结果更接近标准值;非理想的锥形弹簧(即弹簧A和B)测量结果也小于标准值,差异显著性P值分别为0.013和0.007,均小于0.05,说明这种差异也具有明显的统计学意义;非理想柱形弹簧测量结果高于标准值,与标准值差的绝对值最最小,差异显著性P值为0.216(大于0.05),说明测量值与标准值的差没有统计学意义,测量值与标准值差别不明显。所以,柱形非理想弹簧的等效弹性系数是非常合理的,锥形弹簧有效弹性系数的处理方法虽然有一定的合理性,但还有待于进一步修正。 表6 表面张力系数测量值与标准值差异单样本t检验Tab.6 The one-sample t test between measured and standard values of surface tension coefficients 实验过程中,用每个弹簧进行多次测量,因为各种误差,每次测量结果不同,用标准差表示测量精度,标准差越大,测量精度越低;反之,标准差越小,测量精度越高。表7是用不同弹簧测量结果的统计性描述。根据表7的分析结果,无论将弹簧视为理想或非理想弹簧,弹簧A和C对应的表面张力系数单次测量标准差分别具有最小值和最大值,而弹簧B对应的标准差介于两者之间,即柱形弹簧测量精度低于锥形的测量精度。根据前面的分析,用非理想柱形弹簧测量的表面张力系数最接近标准值,即非理想柱形弹簧的测量准确度最高,非理想柱形弹簧单次测量标准差最大(0.50×10-2N/m),其测量精度偏低。 表7 纯净水表面张力系数测量结果统计性描述Tab.7 Statistical description of measurement results of surface tension coefficients of purified water 基于焦利秤和拉脱法,用3中不同类型的弹簧,分别将其视为理想和非理想弹簧测量纯净水在20 ℃表面张力系数,探索金属丝浮力及水膜质量、弹簧类型及弹簧质量对测量结果的影响并分析弹簧类型对测量精度影响;并且提出一种非理想弹簧等效弹性系数的测量方法。 根据分析结果可知:(1)如果将弹簧视为理想弹簧,金属丝浮力及水膜重力对表面张力系数测量结果的影响具有统计学意义,修正前后表面张力系数平均值的差异显著;但在非理想弹簧条件下,这种差异不显著,可以不计水膜重力和金属丝浮力对表面张力系数测量结果的影响。(2)同一类型的弹簧,将其视为非理想弹簧的弹性系数大于相应的理想弹簧弹性系数;非理想弹簧测量的表面张力系数高于理想弹簧的测量结果,而且两者的差异具有明显的统计学意义,说明弹簧质量对测量结果的影响不能忽略。(3)无论是理想弹簧还是非理想弹簧,柱形弹簧测量精度都低于锥形弹簧测量精度。(4)非理想弹簧测量的液体表面张力系数平均值与标准值的绝对误差小于理想弹簧的测量结果,而且这种差异具有明显的统计学意义。如果用绝对误差表示测量准确度的话,那么非理想弹簧测量结果准确度高于理想弹簧测量准确度,说明本文提出的测量非理想弹簧等效弹性系数的方法具有一定的合理性。尤其是对于柱形非理想弹簧,其测量结果与标准值差异没有统计学意义,说明柱形非理想弹簧的等效弹性系数测量方法是非常合理的;但两个锥形非理想弹簧的测量准确度虽然高于相应的理想弹簧测量准确度,但与标准值的差异仍有明显的统计学意义,说明本文测量锥形弹簧等效弹性系数的方法有待于进一步修正。2.2 匀质圆柱形弹簧质心移动距离的计算方法
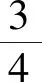
2.3 圆锥形弹簧质心移动距离的计算方法
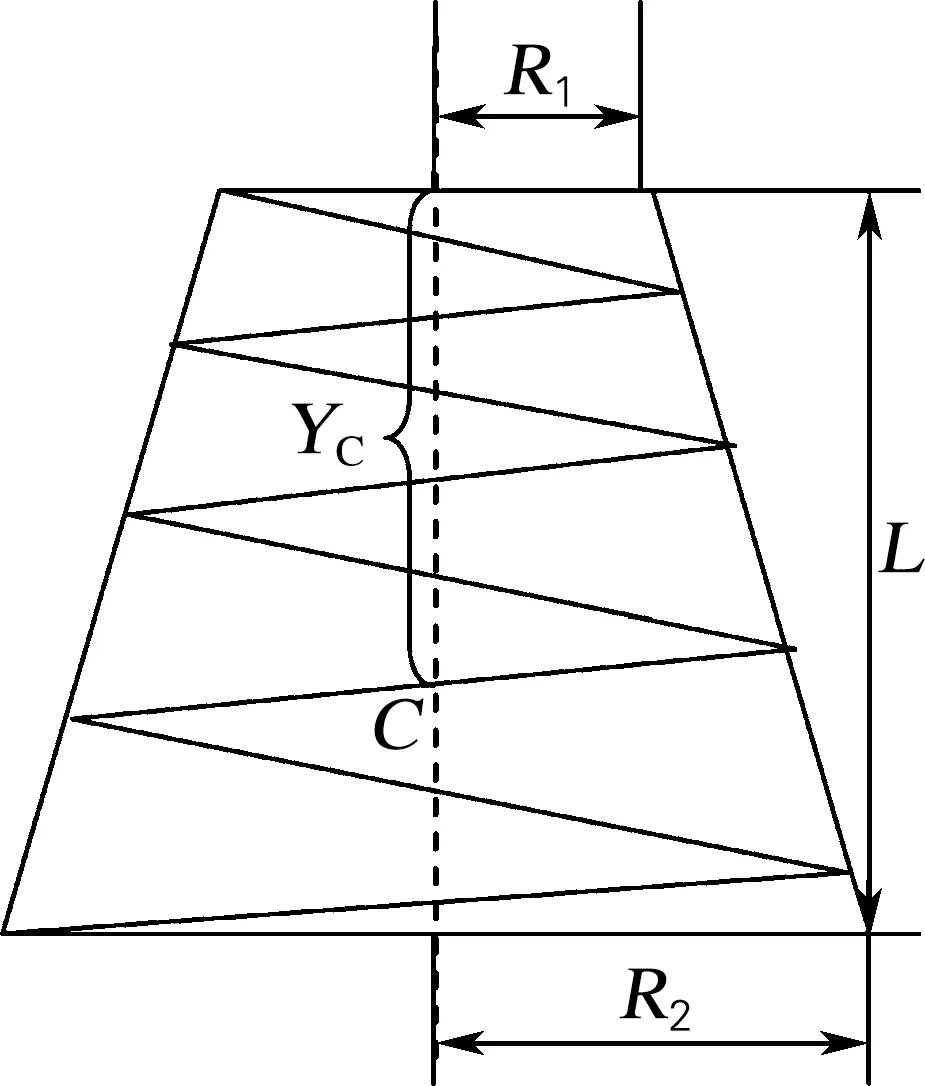
3 实验结果与分析
3.1 理想弹簧和非理想弹簧弹性系数的测量
3.2 计入水膜重力及金属丝浮力前后液体表面张力系数差异性分析


3.3 弹簧弹性系数对表面张力系数测量结果的影响


3.4 不同弹簧单次测量精度分析
4 结 论
