分数阶混沌系统动力学特性分析与DSP实现
2021-03-01刘天明阎慧臻马晨光杨飞飞曹颖鸿
刘天明,阎慧臻,马晨光,杨飞飞,曹颖鸿
(大连工业大学 信息科学与工程学院,辽宁 大连 116034)
0 引 言
近年来的分数阶微积分的相关研究表明,相比于整数阶微积分,分数阶微积分可以更好地描述客观物理世界[1],因此针对分数阶微积分的研究成为热点。针对Chen系统[2]、Liu系统[3]和简化Lorenz系统[4]等非线性混沌系统的研究发现,相比于整数阶混沌系统,分数阶混沌系统具有更为复杂的动力学特性[5-6]。
目前,分数阶混沌系统的求解算法主要有频域法(FDM)[7]、预估校正法(ABM)[8]和Adomian分解法(ADM)[9]。这些算法普遍采用的是黎曼-刘维尔定义和卡普托定义,但它们都存在一些问题:首先是其不能满足整数阶微积分所满足的一些重要性质[10],例如乘积法则和链式法则;其次,计算过程非常复杂[11-12]。因此,Khalil等[13]提出了一种新的分数微积分定义——可整合分数微积分。该分数阶微积分定义和性质与ADM算法相结合可以很好弥补现有算法求解分数阶微分方程的不足[14-15]。CADM算法改进ADM算法,降低了计算的复杂程度,并具备较快的收敛速度、计算速度和较小的资源消耗等优点[10]。CADM算法求解分数阶混沌系统正逐渐成为研究的热点[16-18]。
分数阶混沌系统的应用[19-21]实际依赖信号处理的软硬件技术。数字信号处理器(DSP)以其性能优越、处理方便等优点在工程上得到了广泛的应用。基于此,本研究利用DSP技术,对提出的四维分数阶混沌系统进行了硬件实现。
本研究在一个四维Sprott-B混沌系统的基础上,利用可整合微积分定义构造该四维混沌系统的分数阶形式。基于CADM算法求取该分数阶系统的数值解,对其动力学行为进行了分析,利用0-1测试验证产生混沌最小阶数,同时用SE和C0复杂度算法分析了该系统随机性。最后运用DSP技术对该系统进行了硬件实现。
1 分数阶混沌系统数值分析
1.1 分数阶混沌系统CADM求解算法
设一个分数阶系统方程为
(1)

(2)
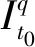
(3)
将系统非线性项进行分解:
(4)
式中:i=0,1,2,…;j=1,2,…。则方程数值解为
(5)
式中:
(6)
1.2 分数阶混沌系统求解
在文献[22]提出的Sprott-B系统的基础上设计了一个新的四维自治混沌系统如式(7)所示。

(7)
式中:x,y,z,w为状态变量;a,b,c为系统参数。
根据分数阶微积分定义,式(7)对应的分数阶系统为
(8)
式中:q为系统阶数。分解式(8)可得其中的线性项、非线性项和常数项分别为
(9)
(10)
(11)
根据式(4)对系统非线性项进行分解,在保证精度的基础上取前6项可得
(12)
(13)
(14)
设该分数阶混沌系统的初值为x0=[x1(0),x2(0),x3(0),x4(0)],展开式第一项为
(15)
同时令
(16)
(17)
令h=t-t0为步长,同时
(18)
则第二项可表示为
(19)

类似地,可得其他5项展开式分别为
(20)
(21)
(22)
(23)
(24)
由此可得此时分数阶混沌系统解为
(25)
2 分数阶混沌系统动力学特性分析
2.1 系统仿真
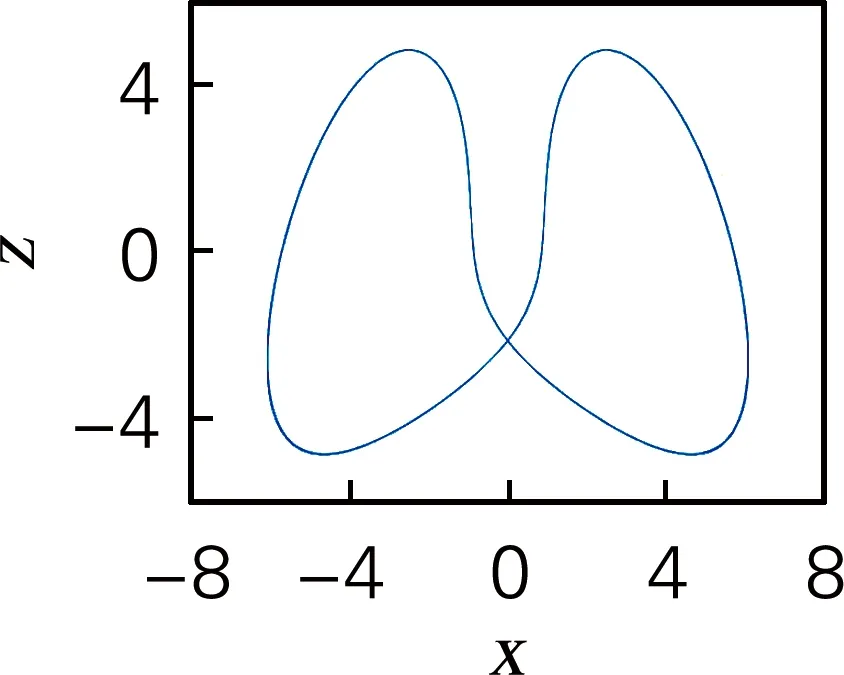
取式(7)系统参数a=4、b=9、c=5和q=0.8,步长h=0.01,x0=[1,1,1,1],系统相图如图1所示。此时李雅普诺夫指数为L1=1.017 0、L2=0、L3=-12.547 9和L4=-16.720 6,系统维度DL=2.09。系统有一个正的李雅普诺夫指数,表明此时系统为混沌态。
此时系统Poincaré截面如图2所示,图中Poincaré截面既不是有限点集,也不是封闭曲线,是一些成片的具有分形结构的密集点,这种结构具备混沌系统的典型特征。

图2 系统y-x平面的Poincaré截面(q=0.8)Fig.2 Poincaré section of the system on the y-x plane (q=0.8)
2.2 系统稳定性分析
(26)
取a=4、b=9和c=5,此时系统平衡点为S1,2=(±3,±3,0,0),系统特征方程为
λ32+9λ24+29λ16+126λ8+360=0
(27)
求解特征方程特征值,若其满足
(28)
则系统在平衡点是渐进稳定的[23]。其中M是分数阶分母的最小公倍数。将特征值代入式(28)得
(29)
表明此时系统特征值满足式(28),所以系统在平衡点S1,2处是稳定的。
2.3 系统参数变化对动力学特性的影响
2.3.1 参数a对系统动力学特性影响
取参数b=9、c=5和q=0.8,仿真步长h=0.01,系统初值x0=[1,1,1,1],当a∈[1,5]时,系统的李雅普诺夫指数谱和分岔图如图3所示。为了更好观察系统特性变化,在图3(a)中舍去了最小的两条李雅普指数曲线。当a在[2.98,3.03],[3.46,3.5],[4.27,4.33]和[4.34,5]范围内取值时,系统最大的李雅普诺夫指数为零,所以a在这些区间内取值系统是周期态。在其他范围内,最大的李雅普诺夫指数为正,系统是处于混沌态。表1总结了当系统随参数a变化时所具有的复杂动力学行为。

(a) x-y平面相图
(a) a=5.00

(a) 李雅普诺夫指数谱

表1 参数a变化的系统状态Tab.1 The system status with a
由表1可知,参数a∈[1,5]时,系统中出现了一种典型的混沌吸引子和6种不同类型的周期态。图4中分别取了周期1(a=5)、周期2(a=4.4)、周期5(a=4.16)和混沌态(a=4)时的相图和0-1测试,图中可以看到当系统处于周期态时,p-s平面上是有界的规则的运动;当系统处于混沌态时,p-s平面上是类似于布朗运动的无界运动。
2.3.2 参数b对系统动力学特性影响
取参数a=4、c=5和q=0.8,仿真步长h=0.01,系统初值x0=[1,1,1,1],图5是系统参数b∈[7,11]变化时的李雅普诺夫指数谱和分岔图。图5(a)同样舍去最小的两条李雅普诺夫指数曲线。从分岔图中可以看到,随着参数b增加,系统通过倍周期分岔从周期态进入混沌状态,同时当参数b在[8.53,8.59]和[10.21,10.25]处时出现两个较为明显的周期窗口,这与李雅普诺夫指数谱是相对应的。

(a) 李雅普诺夫指数谱
如表2所示,系统参数b∈(7,11)时,系统出现了各种不同的动力学行为,有多种类型的周期态和混沌态出现,说明参数b的变化对系统动力学特性有较大的影响。

表2 参数b变化的系统状态Tab.2 The system status with b
2.3.3 阶数q对系统动力学特性的研究
取a=4、b=9和c=5,步长h=0.01,系统初值x0=[1,1,1,1],q∈[0.5,1]。系统随阶数q变化的指数谱和分岔图如图6所示。从图6(a)李雅普诺夫指数谱中可见,当q∈[0.53,1],系统处于混沌状态。当q<0.52时,在分岔图和李雅普诺夫指数谱中均没有数值,系统处于发散状态。

(a) q=0.53

(a) SE复杂度
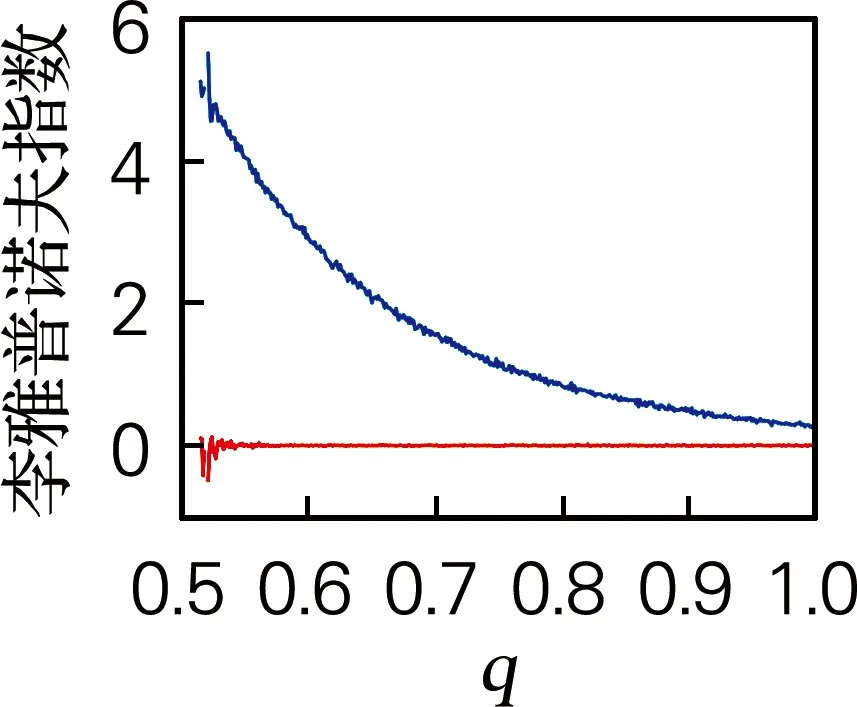
(a) 李雅普诺夫指数谱
为了进一步分析系统适用于保密通信等领域的参数选择范围,更好的观测混沌系统的动力学特性[24-27]。取系统阶数q∈(0.5,1),序列长度N=50 000,此时系统SE复杂度和C0复杂度如图7所示。由图(7)知,当q大于0.52时,SE复杂度和C0复杂度的变化趋势是逐渐减小的,当q=1时,复杂度的值达到最小。可见,分数阶混沌系统是比整数阶混沌系统更为复杂,随着阶数减小,系统复杂度会相应变大,说明该系统的分数阶状态比整数阶状态具有高的应用价值。
由图6可知q<0.52时,系统是发散的,为了验证系统产生混沌的最小阶数,引入了0-1测试。0-1测试的结果如图8所示,当参数q=0.53时,测试结果为类布朗运动,说明系统是混沌的。如图8(b)所示当参数q=0.52时,测试结果为稳定点,说明系统是非混沌的。由此可得系统产生混沌的最小阶数0.53×4=2.12。
3 分数阶混沌系统DSP实现
完成分数阶混沌系统的硬件实现是其实际应用的基础。首先对DSP进行初始化,并进行系统初始设置。然后对系统式(8)进行迭代,将迭代结果数据推送入硬件系统后处理并将结果从DSP中输出,最后使用数据进行初始值的替换并进行迭代,直到结束为止。在数据处理环节,DSP产生的数据被传送入DAC8552中转换成模拟信号传送给示波器。
DSP硬件平台中采用的DSP-芯片为TMS320F28335,采用16位双通道D/A转换器DAC8552对由DSP产生的时间序列进行转换。D/A转换器由DSP通过SPI(串行外围接口)控制,把数字信号转化为模拟信号传送到示波器上显示。
图9为通过DSP平台得到的混沌系统信号相图。此处系统参数a=4、b=9和c=5,系统阶数q=0.8,步长h=0.01,将其与计算机仿真得到的系统相图进行比较,二者结果是一致的。
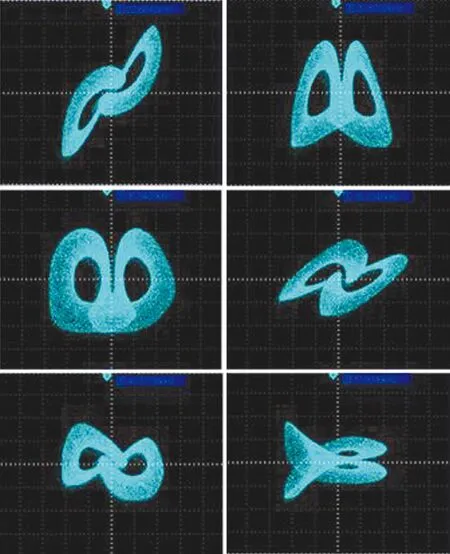
图9 DSP实现系统相图Fig.9 The system phase diagram of DSP implementation
4 结 论
设计了一种四维分数阶系统,采用CADM分解算法求解了该四维分数阶混沌系统的数值解并分析了该系统动力学特性。结果表明,该分数阶混沌系统具有复杂的动力学行为。系统产生混沌的最小阶数为2.12,而且通过复杂度分析可知,当q=0.53时,系统复杂度最高,此时混沌序列随机性最好,安全性能最高。最后在DSP平台上完成了该系统的硬件实现,结果体现了CADM算法的正确性以及分数阶混沌系统的物理可实现性。研究结果为分数阶混沌系统运用于保密通信等领域,提供了理论和实际应用基础。
