核模糊聚类划分子种群的双种群遗传算法

孙雨萌，柏丽娜，张旭秀

(大连交通大学 电气信息工程学院，辽宁 大连 116028)

0 引 言

传统单种群遗传算法[1]在其寻优进化过程中易出现个体多样性下降过快，在进行种间交配时，易出现高适应度种群交配池，造成种群中部分基因信息丢失，产生遗传算法早熟现象。2005年Martikainen等[2]将单一机制的种群进化过程演变成双种群并行进化，选取合适时机进行种间交流。双种群遗传算法正不断应用于工程实践中，例如：时间轨迹优化[3]、配电网参数辨识[4]、作业车间调度[5]和控制器参数优化[6]等。

标准双种群遗传算法在其进化初期采用随机分配的方式对子种群进行划分，变异后以迁移的方式进行种间交流，但其在进化后期仍存在双种群种间同质化的严重缺陷，造成双种群陷入相同的局部最优解。文献[7-9]引入蜂群繁殖结构，在迭代过程中以不断引进新种群的方式来构造双种群，并进行种内斗争获取最优个体作为蜂王与其他个体进行交配，采用个体融合的方式进行种间交流；文献[10-12]引入小种群探测结构，即依据迭代经验，在进化达到一定程度时，取适应度值最高的个体集合，随机对其进行划分成i个并行遗传的小种群，以进化所得最优解替换原集合的方式进行种间交流；文献[13-14]引入战争淘汰结构，采用初始单种群取反的方式构造双种群，迭代过程中以个体斗争淘汰的方式进行种间交流。

蜂群繁殖结构属于嵌套循环结构，小种群探测结构属于经验划分，战争淘汰结构需在个体转化为二进制条件下进行，因此，算法计算过程较为复杂，且严格限制了缺乏经验的工程人员的应用。吸取上述双种群遗传算法改进思路，为解决种群同质化的严重缺陷，同时加快迭代进化所需时间，本研究给出一种核模糊聚类划分子种群的双种群遗传算法(KFC-2PMGA)，使子种群划分不再是一种随机行为，而是以个体适应度值为依据，利用核模糊聚类算法将满足不同约束条件的个体划分到子种群中，并对个体中基因位分别采取改进的自适应交叉及变异策略，使得改进后的双种群遗传算法更易保留基因多样性，同时具备局部及全局搜索能力。

1 标准双种群遗传算法

标准双种群遗传算法[2]在单种群遗传算法的基础上，对初始群体进行随机划分，得到个体数目相等的两个子种群，分别按照不同的交叉及变异概率进行遗传操作。其中子种群1交叉及变异概率均较小，称为开发种群，用于发掘个体中局部最优值，提高收敛速度；子种群2交叉及变异概率均较大，称为探测种群，用于扩大搜索面积，提供新的可行解，克服过早收敛。在进化过程中，两个子种群均独立进化，并引入迁移算子进行种群间基因交换，算法具体步骤为：

步骤1初始化染色体个数2N个，随机划分双种群，确定交叉概率Pc1、Pc2及变异概率Pm1、Pm2；

步骤2计算群体中染色体适应度值；

步骤3判断适应度值是否满足收敛条件，若满足收敛条件则输出其全局最优解，若未满足则转步骤4；

步骤4并行子种群按照交叉概率Pc1、Pc2进行交叉操作；

步骤5并行子种群按照交叉概率Pm1、Pm2进行变异操作；

步骤6进行中间迁移，产生新一代种群，转步骤2。

2 基于核模糊聚类算法的双种群遗传算法

2.1 双种群划分方式的改进

传统双种群遗传算法在进行种群间划分时，往往将初始种群随机分割为两个子种群，虽在一定程度上对传统单种群遗传算法做出优化，但未能避免迭代后期出现子种群同化的现象[15]。

核模糊聚类算法(KFCM)以模糊聚类算法(FCM)为主要依据，利用核函数替换传统FCM算法中欧的距离，使聚类效果更加完善[16-17]。将核模糊函数引入遗传算法子种群划分中，将个体适应度值作为聚类划分的约束条件，取{xi，i=1，2，…，n}表示种群内个体适应度值集合，m为预设聚类子种群数目，{vj，j=1，2，…，m}为子种群聚类中心，φ为非线性映射函数，φ(x)为高维空间中x的原象，则向量的欧氏距离定义为

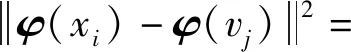
K(vj，vj)

(1)

其中K(x，v)=φ(x)Tφ(v)为核函数向量内积，结合高斯核函数，可得式(2)，K(x，x)=1。

(2)

取zij函数表示第i个样本点隶属于第j个聚类程度，取c为模糊加权指数，决定本次聚类效果的模糊程度。c取值为常量，则KFCM目标函数定义为

(3)

将高斯核函数引入目标函数可得

(4)

(5)

更新后新种群聚类中心为

(6)

根据推导公式，利用核模糊C均值算法聚类划分双种群步骤为

步骤1设定参数n，m，c初始值，初始化聚类中心vj，初始隶属度函数zji，使其满足规定约束条件；

步骤2计算核矩阵K(x，y)；

步骤3利用式(5)更新后的隶属度函数；

步骤4利用式(6)计算该隶属度函数下的聚类中心；

步骤5利用式(3)计算KFCM目标函数，如果目标函数数值变化小于某一设定阈值，则算法停止，输出聚类划分后双种群，适应度值较高的种群称为精英种群，适应度值较低的种群称为平民种群，否则跳转至步骤2。

2.2 自适应基因位交叉策略

聚类划分所得双种群在进行种群内部交叉时，基于单点交叉方式，应用一种简单的单点横向交叉方式[18]，交叉概率依据种内个体基因相似度采取一种动态自适应的交叉算子。

为提高种群的局部搜索能力，在进行种内交叉时，精英种群交叉概率与种内个体相似性正相关，提高精英种群搜索最优解的效率。平民种群交叉概率与种内个体相似性负相关，扩大搜索范围，以便寻求新的搜索空间，有关基因相似性的求解参考文献[19]。

2.3 自适应多位变异策略

为确保种群内样本个体的多样性，遗传算法引入变异操作，将交叉后的部分个体基因进行按位取反。针对交叉操作所得的双种群，采用一种改进的自适应多位变异算子。对于精英种群，在算法早期极少的基因位发生变异，充分发挥相似个体间高交叉概率的性质，进行空间搜索，在算法迭代到一定次数，交叉作用不显著时，增大变异位数，防止算法过早陷入局部最优解。对于平民种群，算法早期引入大变异算子，增加样本的多样性，当算法趋于稳定，减小变异位数，保留部分当前代数平民种群中产生的高适应度基因。在逐次迭代过程中，可依据新的核模糊聚类中心，进行精英种群与平民种群间的基因流动。同时依据个体的适应度情况决定变异位数，适应度值与变异位数呈反比，减少对优秀基因的破坏。改进的自适应变异位数如式(8)所示，

(8)

其中bit1表示精英种群变异位数，bit2表示平民种群变异位数，Sn表示最终稳定的变异位数，Sc表示交叉效果不显著时的迭代次数，t表示当前迭代次数，f表示当前个体适应度情况，fmin与fmax分别表示适应度最小与最大值。

2.4 改进双种群遗传算法流程

基于核模糊聚类划分子种群的动态自适应双种群遗传算(KFC-2PMGA)具体迭代步骤为

步骤1初始化种群规模P，子种群个数K，核模糊C均值聚类算法各初始参数，终止迭代次数T。

步骤2计算种群中所有个体适应度值。

步骤3求取满足条件的KFCM目标函数，进行种群内部所有个体核模糊聚类分析，划分双种群。

步骤4依据其个基因间相似度进行自适应交叉操作。

步骤5依据自适应多位变异算子进行自适应变异操作。

步骤6未收敛或未达到迭代次数，将双种群进行合并，转步骤2，否则转步骤7；

步骤7输出最优个体作为最优解，进化过程结束。

3 实验仿真及结果分析

3.1 测试函数及参数设置

为验证所改进双种群遗传算法的可行性与有效性，分别选择一元单峰、多峰测试函数及二元单峰、多峰测试函数进行仿真验证，并对比标准双种群遗传算法[2](2PMGA)及自适应双种群遗传算法[20](A-2PMGA)，测试函数见表1。

表1 测试函数Tab.1 The test function

实验算法中群体规模设置为200，维数设置为30维，函数f1、f4、f6最大迭代次数为200代，函数f5、f7最大迭代次数为100代，函数f2最大迭代次数为1 000代，函数f3最大迭代次数为400代。参数设置为：标准双种群遗传算法中，Pc1=0.1、Pc2=0.9、Pm1=0.01、Pm2=0.6。

3.2 仿真结果分析

对每种算法独立运行100次，并对100次的运行结果进行统计，仿真结果见表2、图1～7。

表1中，函数f1～f3为一元测试函数，其中Sphere函数为一元单峰函数，函数结构较为单一；Ackley函数为一元多峰函数，该测试函数存在大量的由余弦调制波构成的多峰或多孔，曲面起伏不平，函数搜索十分复杂，易落入局部最优陷阱；Girewank函数为一元多峰函数，各变量之间影响严重、显著相关。依据表2中f1、f2数据可得，3种优化算法虽均未寻到其全局最优解，但改进算法KFC-2PMGA平均收敛代数远小于其余2种算法，且平均收敛值精度较高，依据图1～2可得，KFC-2PMGA算法具有更快的搜索速度。依据表2f3可得，KFC-2PMGA在迭代过程中可跳出局部最优点，搜索到全局最小值。

函数f4～f7为二元测试函数，其中Bohachevsky 函数为二元单峰函数，各变量之间相互独立；Holder Table函数全局最优解周围存在很多局部极值点，因此难以找到全局最优；Drop-Ware函数具有多模态，函数结构高度复杂；Shuber函数各变量之间的相关性较强，且存在误导算法方向的梯度信息，全局共存在760个局部极值点。依据表2f4～f7数据可得，2PMGA在其收敛时产生“早熟”现象，A-2PMGA及KFC-2PMGA算法在求解多峰问题时有更好的收敛精度，KFC-2PMGA算法收敛精度最高；依据图4～7可得，KFC-2PMGA算法具有较快的收敛速度。

表2 函数f的运行仿真结果Tab.2 Simulation result of function f

综上可得核模糊聚类子种群的划分方式降低了种群间同化的可能性，依据个体间相似度进行自适应交叉操作增加了算法的收敛速度，引入多基因位自适应变异算子使得种群内个体多样性得以提高，改进算法中后期性能。

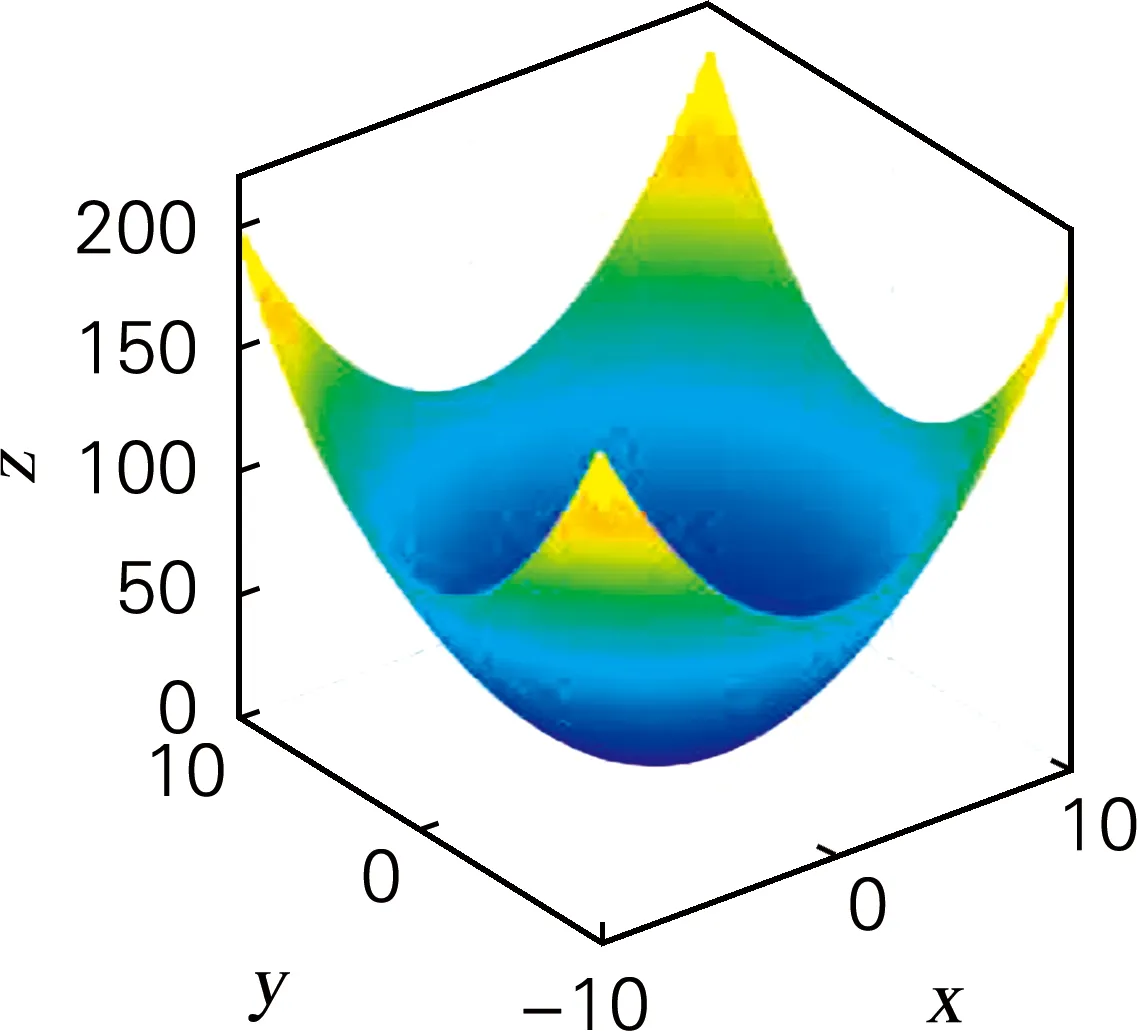
(a) 函数Sphere三维图

(a) 函数Ackley三维图

(a) 函数Griewank三维图

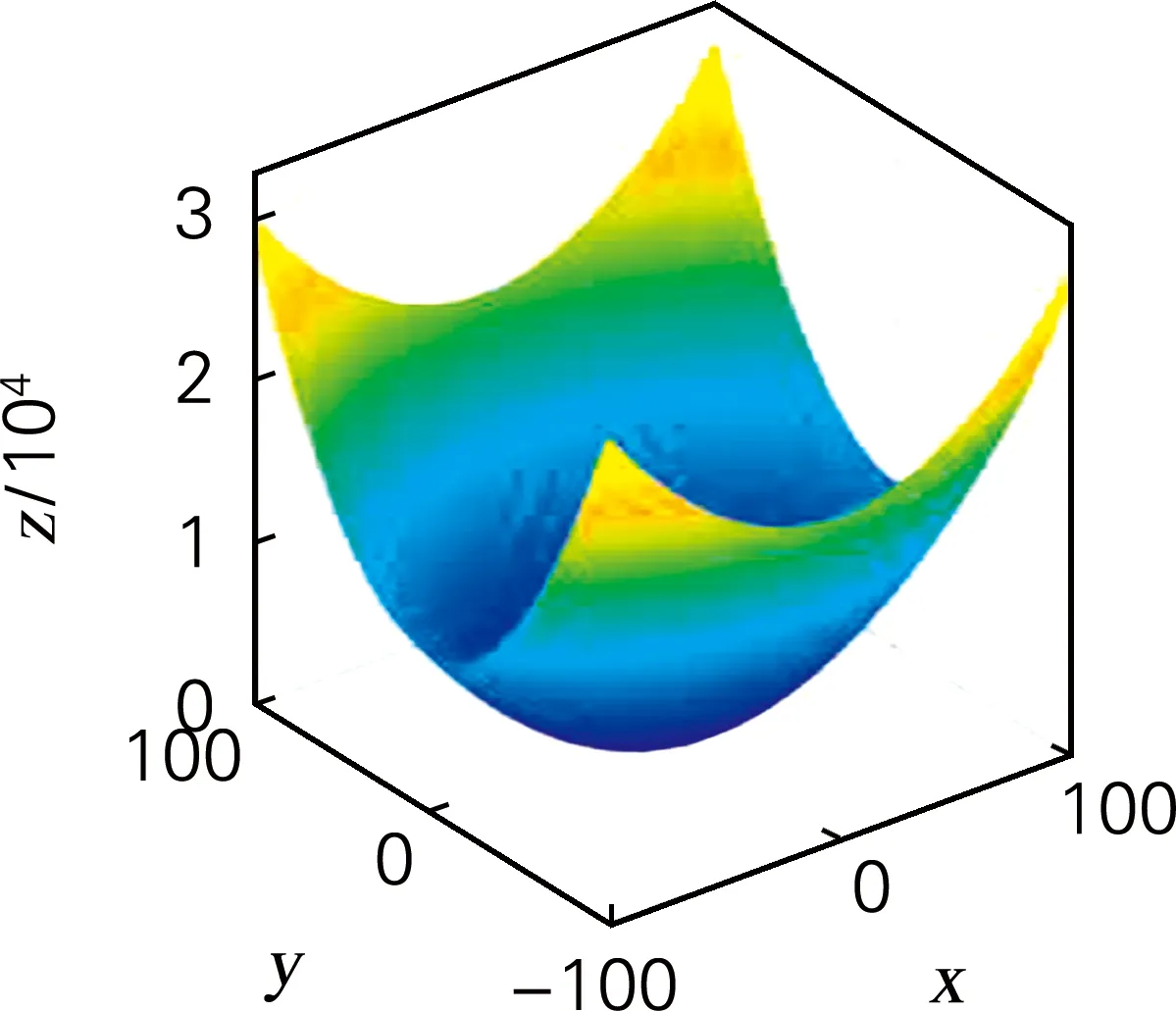
(a) 函数Bohachevsky三维图

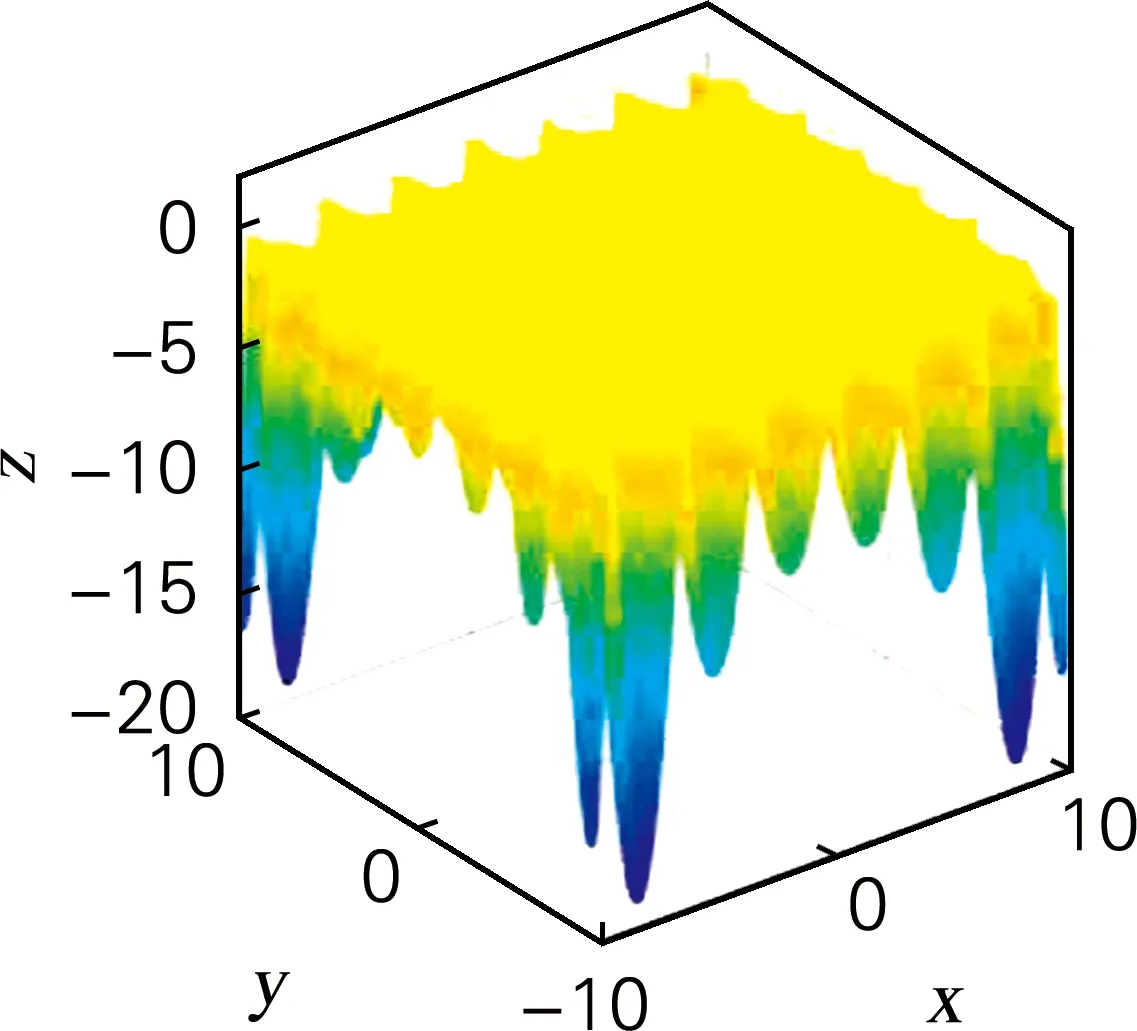
(a) 函数Holder三维图

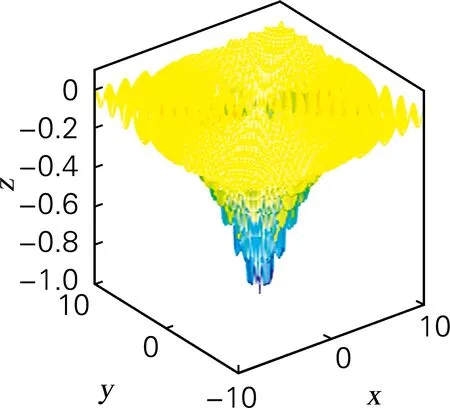
(a) 函数Drop-Wave三维图

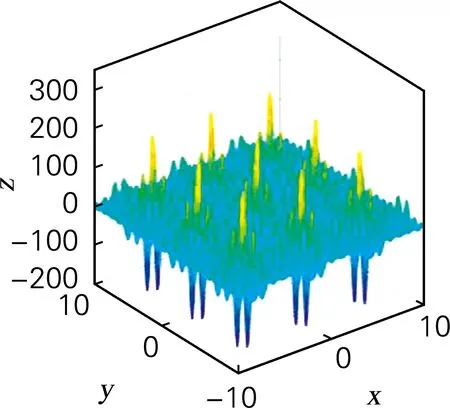
(a) 函数Shubert三维图

4 结 论

提出了一种核模糊聚类划分子种群的双种群遗传算法，将其个体适应度值设定为核模糊聚类算法的输入，依据KFCM目标函数将初始种群进行划分，分为精英种群与平民种群，子种群内依据个体相似度进行自适应交叉操作，引入多基因位变异算子，扩大种群搜索范围，将变异操作后子种群进行种间合并，重复上步骤，实现子种群间精英与平民个体的相互流动，将双种群遗传算法本身的并行性充分发挥出来。采取一元、二元、单峰及多峰测试函数进行验证，结果表明改进的KFC-2PMGA算法能有效避免子种群陷入同质化，在收敛速度及收敛精度上有了显著提升，对比传统2PMGA算法及A-2PMGA算法能更加高效地搜索到全局最优解。