基于中微尺度耦合模式的风电场风资源评估方法研究

应 有， 申新贺， 姜婷婷， 陈广宇， 陈 晨

（1.浙江运达风电股份有限公司， 浙江 杭州 310012； 2.浙江省风力发电技术重点实验室， 浙江 杭州 310012）

0 引言

风资源评估是风电场开发的核心环节，对风电场效益及风电场投资的成败起着重要的作用，因此， 对风电场的风资源特性进行准确评估，是当今风电工程领域不可忽视的问题。 随着我国风力发电的上网电价逐年下调，风电场的盈亏几乎触及平衡点，对风资源评估方法的精确性提出了更为苛刻的要求。

风资源评估可以分为宏观和微观两个尺度。宏观尺度的评估是指在一个较大的区域范围内，采用中尺度气象模式（Weather Research Forecast，WRF）对宏观大气流动进行模拟，以获得该区域风资源的时空分布特性[1]。 中尺度模式对于分析宏观的风资源分布有很好的指导作用[2]，[3]，然而其空间分辨率较大（1 km 量级），无法求解大气边界层与风电场甚至风力机间的相互作用，无法精确评估风电场内风电机组的风资源状况。 微观尺度的评估是指在风电场范围内，采用计算流体力学（CFD）方法获得风电场内部区域的流动问题和风资源状况。 学者对微尺度风资源评估方法开展了深入的研究，在湍流计算、尾迹流动计算、复杂地形计算等方面均提出了较为成熟的方法和模型[4]～[6]。 CFD 方法的优点是可以实现10 m 量级的分辨率， 精确评估各风电机组的风资源状况，然而其计算入流边界条件时大多采用假设的入流风廓线模型， 无法考虑大范围大气环流对风电场内风流的影响， 因而无法评估真实大气边界入流条件下风电场的流动及运行特性， 导致相关研究成果在工程应用上存在局限。因此，必须将中尺度评估与微尺度评估相结合， 才能实现风电场风资源的精准评估。

风电场中微尺度耦合数值模拟主要有3 种模式。 第一种是在中尺度框架下结合微尺度模型进行降尺度计算。 方艳莹[7]将WRF 与CFD 软件Meteodyn WT 相结合， 开展了海岛地区的风资源评估研究。何晓凤[8]将MM5 与CFD 软件相结合开展了复杂地形的风能资源评估研究。该模式中，中尺度模拟结果向微尺度模型提供虚拟测风数据，实际上并未改善微尺度模型的入流边界条件，因此并非真正意义上的耦合。 第二种模式是将中尺度模式与大涡模拟方法进行嵌套耦合。 Talbot C[9]利用WRF-LES 将模式水平分辨率由10 km 降至50 m。 Liu Y[10]通过六层嵌套对某实际风电场开展了大涡模拟对于风电场模拟结果的影响研究。 限于大涡模拟方法庞大的计算量， 该模式不能采用较精细的计算网格， 限制了其在风电工程领域的发展。 第三种模式是将中尺度模式与基于RANS（Reynolds-Averaged Navier-Stokes Equations）方法的CFD 模型进行嵌套耦合， 利用中尺度模式为CFD 方法提供真实边界条件，从而实现对风场的精细化模拟。 Virk[11]和程雪玲[12]的研究结果表明，中尺度模式与微尺度CFD 模型的耦合模式具有较好的发展前景，然而，现有的研究成果较少，特别是针对嵌套耦合模式、入流边界条件构建方式以及上述方法在实际风电场中的验证和应用的研究还不够深入。

针对这一现状， 本文基于中尺度WRF 模式和微尺度CFD 模型，研究两种方法的耦合模式和入流边界条件的构建方式，建立基于中微尺度耦合模式的风电场风资源评估技术。 同时，通过某复杂地形风电场，结合多测风塔互推的验证方式，对中微尺度耦合风资源评估技术进行分析和验证，以期为风力发电评估提供参考。

1 中尺度和微尺度风资源评估方法介绍

1.1 基于WRF 模式的中尺度数值模拟方法

本文中尺度模式内核采用WRF 计算模型。WRF 是一个被广泛使用的气象模型，可以在绝大多数的并行计算机上使用，并且可以实现灵活的内存划分和支配。 目前，有两个不同的WRF 求解器模型，用于科学研究的WRF-ARW 模型和用于业务的WRF-NMM 模型。 本文选择使用WRFARW 模型，因为从数值模拟计算层面来讲，该模型已经被广泛地验证了其有效性，而WRF-NMM模型则在某些方面还存在着争议 （尤其是在Arakawa 分类中使用E 类型网格计算的时候）。

1.2 基于CFD 方法的微尺度风资源评估方法

微尺度CFD 风资源评估计算方法将现场测风数据和CFD 仿真计算相结合评估风电场风况，进而评估发电量。

通常按风向等角度划分为至少12 个入流风向进行CFD 仿真计算。CFD 仿真采用运达股份基于开源OpenFOAM 软件自主研发的风电场流动仿真分析软件。 采用雷诺平均方程和修正的k-ε两方程湍流模型求解风电场大气边界层流动，采用SIMPLE 算法求解输运方程， 采用结构化网格对风电场计算域进行离散化。 在大气边界层中的表面边界层中， 计算模拟区域的入口风廓线呈对数律形式， 而在上边界层中则由Ekman 法则定义。对于底层网格，地表摩擦力的影响通过在动量方程中引入吸收项来实现。

原始测风数据通常来源于风电场内的测风塔， 测风时长在1 a 以上。 根据流场雷诺相似原则，结合由CFD 仿真得到的测风塔与风力机的风况相关关系以及测风数据， 计算风力机轮毂高度处的风况信息。

风力机发电量AEP 根据风力机轮毂高度处的风速、风速分布频率和动态功率曲线计算得到。

式中：P[uh（t）]为动态功率曲线；T 为1 a 或多年的10 min 或60 min 间隔时间序列；uh（t）为每个时间点的轮毂高度处的风速。

2 基于中微尺度耦合模式的风资源评估技术

2.1 中微尺度耦合风资源评估计算流程

基于中微尺度耦合模式的风资源评估技术的计算流程如图1 所示。

图1 基于中微尺度耦合模式的风资源评估技术计算流程Fig.1 Wind resource assessment process based on meso-microscale coupling model

基于中尺度WRF 模式和微尺度CFD 方法，建立基于中微尺度耦合模式的风资源评估技术的原理如下。

①以气象再分析数据作为背景场， 采用中尺度WRF 数值模拟技术对包含风电场区域的大范围区域进行计算，获得水平分辨率为1～3 km 的中尺度气象分析数据， 本文主要采用EC 再分析数据源。

②基于中尺度模拟结果提取微尺度建模计算边界附近的风速廓线信息，为微尺度CFD 模型提供更真实准确的入流边界条件。

③驱动CFD 模型进行数值模拟，进而进行风电场风资源评估。

2.2 入流边界条件的构建方式

从中尺度模拟结果中提取微尺度建模计算边界附近的风速廓线，并构建入流边界条件。

①提取中尺度模拟结果。 针对不同风向的微尺度计算，计算区域的入口被分割多段，应用不同的风速廓线， 在每一段中沿着风向在计算域边界上游6 km～下游2 km 内选取中尺度点，如图2 所示。

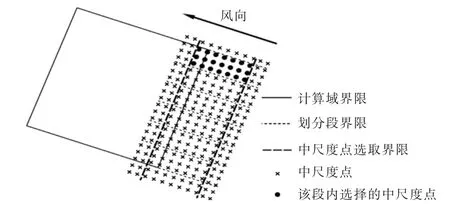
图2 微尺度计算提取中尺度风廓线示意图Fig.2 Schematic diagram of mesoscale wind profile extraction

②基于中尺度模拟结果构建风速廓线。 基于中尺度模拟提供的不同位置、 不同高度的风速信息，对上述多段位置对应的入口风廓线进行计算。在每一个高度内， 一点处的速度由不同方向插值得到， 平均风速由这些点与段之间的距离加权计算得到。

③构建入流边界条件。 对每一条廓线进行归一化处理， 然后通过不同段之间的插值计算得到每一个微尺度计算网格的风速， 从而构建入流边界条件。

3 风电场实例验证及分析

本文针对河南省某大范围复杂山地风电场，分别采用传统微尺度风资源评估方法和中微尺度耦合方法进行了风资源评估， 并采用多测风塔互推的验证方式， 验证中微尺度耦合技术的精确性和可靠性。

3.1 风电场概况

风电场示意图如图3 所示。 选择风电场范围内的6 个测风塔作为验证测风塔，分别是1181#，1524#，1525#，1526#，1527#和7768#，测风塔的测风时间均在1 a 以上。

图3 风电场示意图Fig.3 Diagram of the wind farm

3.2 计算参数设置

中尺度WRF 模拟采用三层嵌套网格技术，网格分辨率和网格格点数如表1 所示。

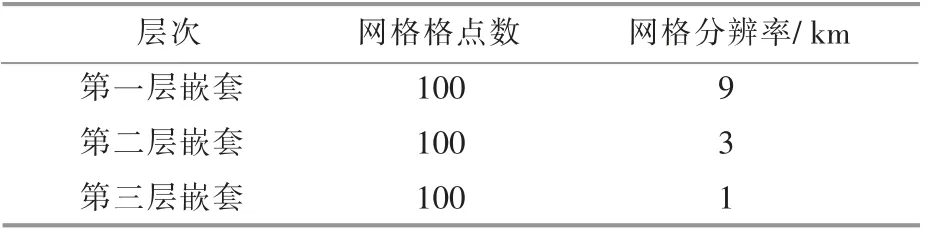
表1 WRF 计算网格方案Table 1 The grid scheme of WRF

计算时须要特别关注大气边界层（ABL）和近地层（SL）的参数化方案，根据众多研究成果[13]，确定了最优参数化方案，其中，近地层的参数化方案采用Monin-Obukhov 方案[14]，大气边界层则采用YSU 方案[15]，其他参数化方案选择如表2 所示。

微尺度CFD 计算模型的高度为1 km。 CFD计算时，按风向等角度划分了12 个入流风向进行计 算，分 别0，30，60，90，120，150，180，210，240，270，300°和330°。

3.3 入流边界条件对比与分析

在中微尺度耦合计算中， 根据中尺度模拟结果构建微尺度计算边界处的入流风速廓线， 并与传统大气对数风廓线模型进行对比。 针对不同风向，分别提取风廓线；针对特定风向，微尺度计算区域的入口按照水平间隔3 km 被分割成多段，每段提取一个入流风廓线。 以主风向D150 为例，共提取8 段入流风廓线，基于30 m 高度的风速进行归一化，并与传统大气对数风廓线进行对比，结果如图4 所示。

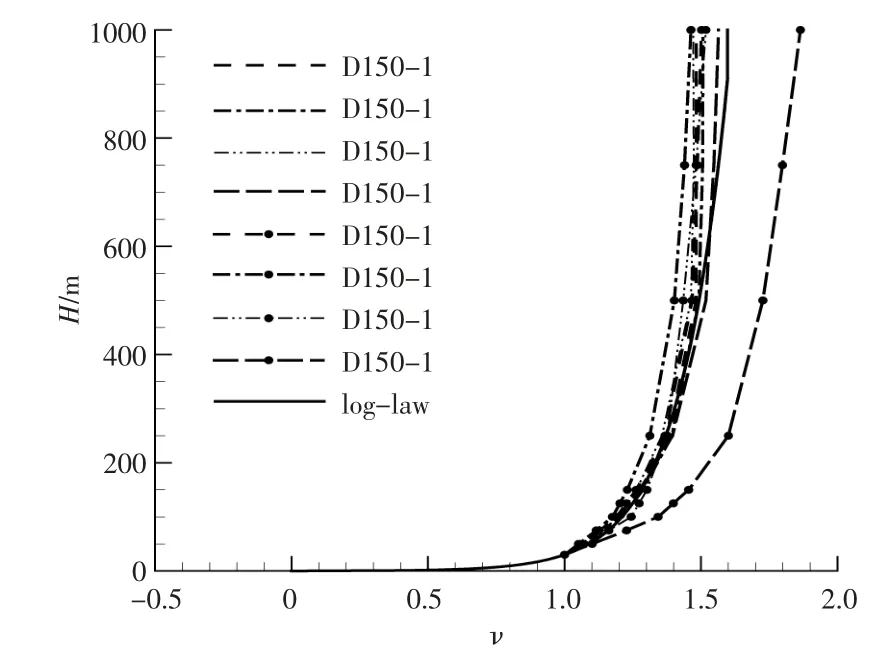
图4 D150 风向的入流风廓线与传统对数风廓线对比Fig.4 The vertical profile comparison of WRF and tradational log-law method at direction 150

不同风向下，基于30 m 高度的风速进行归一化， 取各风向下的第1 段风廓线并与传统大气对数风廓线进行对比，结果如图5 所示。

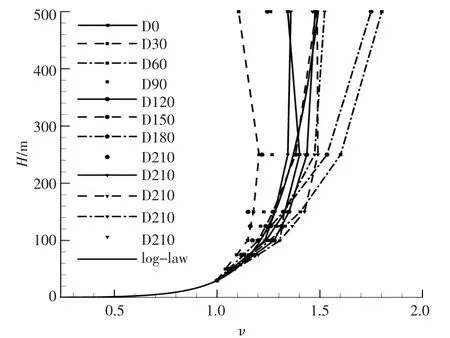
图5 不同风向下的入流风廓线与传统对数风廓线对比Fig.5 The vertical profile comparison of WRF and tradational log-law method at different direction

由图4，5 可知：不同风向下，入流风廓线存在较大差异；同一风向、不同水平位置处，入流风廓线也存在差异，差异幅度相对较小；由于受到大气和地形的影响，大气风廓线存在较大变化，并不能由统一的风廓线模型进行描述。

3.4 风资源评估结果对比与分析

首先，采用微尺度CFD 风资源评估方法在中性热稳定度下进行风资源计算， 并根据计算结果和实际测风数据计算风速评估误差，结果见表3。表3 中，第一行数据代表由测风塔1181 外推至其他各测风塔， 通过评估结果和实际测风结果计算出风速误差，以此类推。 整体平均误差为3.89%。

采用中微尺度耦合风资源评估方法对该风电场进行风资源评估。 各测风塔互推的风速误差如表4 所示，整体平均误差为2.82%。

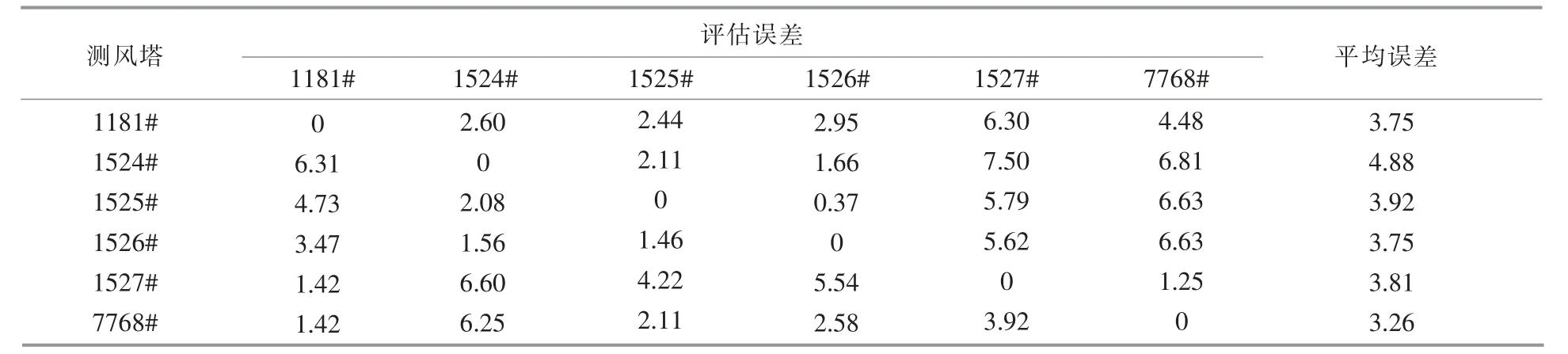
表3 微尺度CFD 风资源评估方法的风速评估误差Table 3 Error of the CFD wind resource assessment method %

表4 中微尺度耦合风资源评估方法的风速评估误差Table 4 Error of the meso-microscale coupling model %

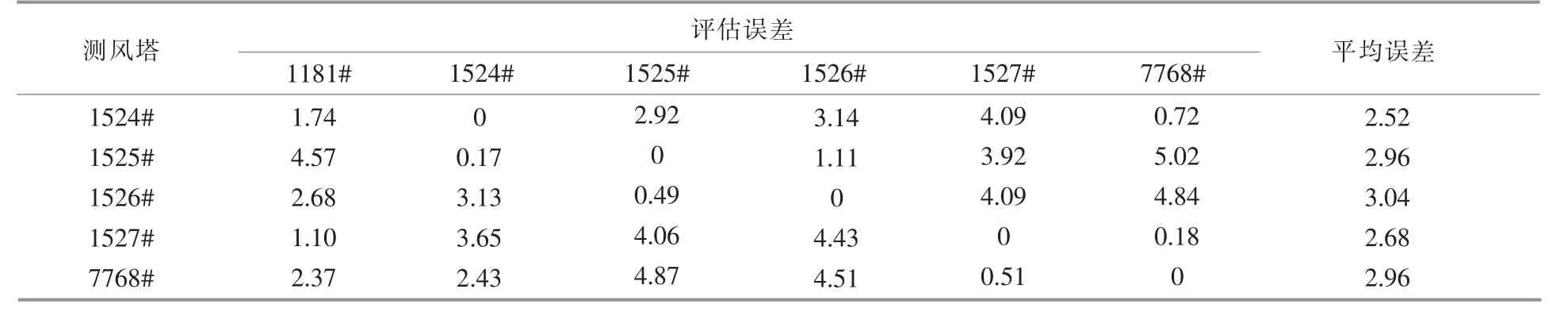
续表4

实测数据验证结果表明， 相比于传统微尺度CFD 风资源评估方法，中微尺度耦合方法降低了风速评估误差，能够改善微尺度CFD 模拟的入流边界条件。

4 结论

本文基于中尺度WRF 数值模拟方法和微尺度CFD 数值模拟方法，研究了中尺度和微尺度的耦合原理， 构建了从中尺度模拟结果中提取微尺度建模计算边界附近的风速廓线的方法， 最终建立了基于中微尺度耦合模式的风电场风资源评估方法。在复杂地形风电场中，采用多测风塔互推的验证方式， 对中微尺度耦合风资源评估方法进行了分析和验证。结果表明，中尺度模拟结果可以有效地对微尺度CFD 模型的边界条件进行校正，使边界条件更接近实际情况， 从而提高风资源评估的准确性。