含分布式发电并网虚拟发电厂鲁棒优化经济调度方法
2021-02-27李国号卢小海周哲民
潘 斌, 方 嵩, 李国号, 卢小海, 周哲民, 王 鹏
(1. 广东电网有限责任公司中山供电局, 广东 中山 528400; 2. 清华大学 电机工程与应用电子技术系, 北京100084; 3.北京清大高科系统控制有限公司, 北京102208)
0 引言
近年来,电力系统中涌现了数量众多、种类丰富的分布式发电资源(Distributed Energy Resources,DERs), 其灵活可调的运行特性以及出力的波动性为电力系统带来了机遇和挑战[1],[2]。当分布式发电在电力系统中的配置较为集中时, 一般采用微电网或者主动配电网的形式进行集成管理; 当分布式发电的分布不适合构成一个统一的系统时,采用传统的微电网或者主动配电网形式难以实现管理。 在这种情况下,虚拟发电厂(Virtual Power Plant, VPP) 作为整合相对分散的分布式发电资源并实现管理的重要手段得到了蓬勃发展[3]~[5]。
VPP 采用先进的量测技术和自动化技术实现了对分布式发电的运行状态采集、 能量管理指令发布和制定、继电保护整定实施等功能。与微电网不同的是,VPP 中分布式发电在实际的分布中可能并不适合看作一个整体的模块, 一般通过智能电网技术将以上资源整合为一个模块实现管理。同时,VPP 中不仅包含分布式发电并网,也配置了包括储能设备、 需求侧管理资源等灵活可调的源荷资源实现对系统的调节[6],[7]。
目前,已有一些文献针对VPP 制定了经济调度模型。文献[8]将VPP 的运行计划和参与电力市场的竞价策略进行协调, 考虑了与系统中需求侧管理资源的互动效应。文献[9]针对VPP 运行问题制定系统内各个分布式发电资源的出力分配计划, 运用模仿者动态算法对所建立的模型进行求解,有效提高了内部功率分配效率。 文献[10]侧重于VPP 参与电力市场的竞价过程制定参与策略,该VPP 在包含传统发电资源的基础上还面向电动汽车,充分利用了电动汽车的调节特性。 然而,目前还很少有文献采用鲁棒优化理论建立VPP最优经济调度模型。 鲁棒优化作为一种考虑区间不确定性的模型, 能够提升系统运行计划的鲁棒性[11],[12]。
本文针对VPP 最优经济调度问题,采用鲁棒优化理论构建系统经济调度模型。以VPP 综合运行收益最大为目标函数,计及机组组合约束、储能充放电约束、 功率平衡约束等必要约束条件建立模型。 基于风光出力区间不确定性构建自然决策者和系统决策者的博弈过程, 采用两阶段松弛法将鲁棒优化模型转化为有限可解的步骤, 最后通过一个算法验证了模型的有效性。
1 VPP 最优经济调度
1.1 目标函数
VPP 最优经济调度模型的目标函数为最大化系统在调度时间内的综合运行收益, 该收益主要来自VPP 向电力系统供电获得的电费收入和可再生能源发电补贴, 并减去包括发电机组的运行成本、环境折算成本、发电机组的启停成本、风电光伏机组运行维护成本在内的VPP 运行成本。
目标函数为
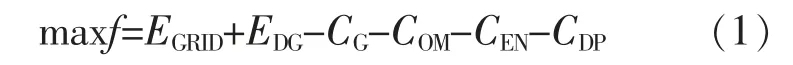
式中:f 为目标函数;EGRID为VPP 与电力系统交换功率获得的收益;EDG为VPP 获得的可再生能源发电补贴;CG为火电机组运行成本;COM为设备运行维护成本;CEN为环保折算成本;CDP为设备折旧成本。


1.2 约束条件
①功率平衡约束
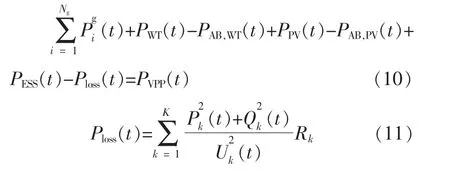
式中:PESS(t)为t 时段储能充放电功率,大于零为放电;Ploss(t)为t 时段网损功率;PVPP(t)为t 时段电力系统能量管理中心分配给VPP 的出力;Pk(t),Qk(t)分别为t 时段馈线k 的有功和无功;K 为馈线数目;Rk为馈线k 电阻;Uk(t)为t 时段馈线k 电压幅值。
②发电机组运行约束
该约束包括机组启停约束、 机组爬坡率约束以及机组出力约束。

③弃风弃光约束

2 区间不确定性与鲁棒优化建模
2.1 VPP 鲁棒优化经济调度
光伏出力和风电出力采用区间形式进行不确定 性 描述[13],[14]。

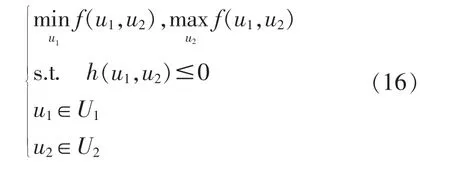
将VPP 能量管理中心看作系统决策者,将VPP 中风电出力和光伏出力不确定性看作自然决策者。 令两者进行博弈,得到VPP 最不利情况下的优化运行场景。 考虑到系统决策者和自然决策者之间的博弈,得到基于鲁棒优化的VPP 最优经济调度模型为式中:博弈的支付f()即为式(1)所示的VPP 运行成本, 对于系统决策者来说需要制定策略最小化该成本, 对于自然决策者来说需要制定策略最大化该成本;u1为系统决策者的控制变量,包括机组启停计划、机组出力计划、储能充放电计划与电力系统交换功率计划;u2为自然决策者的控制变量,包括满足区间不确定性的风电出力和光伏出力。

2.2 两阶段松弛法与鲁棒优化求解
针对基于鲁棒优化建立的VPP 最优经济调度模型采用两阶段松弛法设计求解流程[12],具体的求解步骤如下。

式中:λ 为对偶变量;σ 为辅助松弛变量。
不等式约束f (u1,u2,i)-λh (u1,u2,i)≤σ 有n个,每一个均对应VPP 最优经济调度模型中的整组约束。 求解得到模型的最优解以及控制变量为(u1,n,λn,σn)。
③基于步骤②得到的(u1,n,λn,σn),以自然决策者的视角求解如式(20) 所示的最大值规划问题,得到最优解为u2,n+1,同时得到目标函数f(u1,n,u2,n+1)-λnh(u1,n,u2,n+1)。
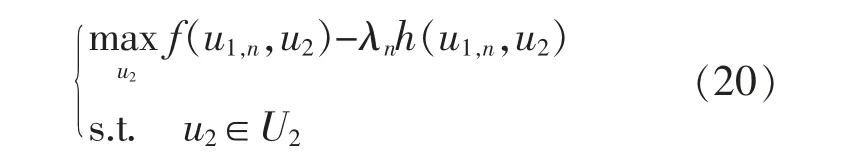
④如果存在足够小的正数ξ,使得f(u1,n,u2,n+1)-λnh(u1,n,u2,n+1)≤σn+ξ,则求解流程结束,得到u1,n,u2,n+1为鲁棒优化模型的最优解; 否则,令迭代次数n=n+1,返回步骤②,在式(19)中增加式(21)所示的约束。
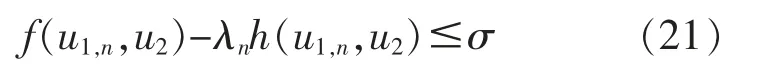
以上基于两阶段松弛法设计的模型求解流程能够在有限步骤内收敛[15]。
3 算例分析
3.1 仿真算例设置
以某地区典型的VPP 为对象,基于所建立的VPP 最优经济调度鲁棒优化模型制定优化运行计划。 该VPP 中配置的分布式风电容量为500 kW,分布式光伏发电容量为600 kW,储能设备容量为1 MW, 储能最大充放电功率为250 kW,储能充放电效率均为0.95,自放电系数为0.02。VPP中配置了G1 和G2 两台燃气发电机组,其中,G1的容量为1.5 MW,G2 的容量为1.8 MW。 燃料成本 函 数 中,G1 的a1,b1,c1分 别 为0.039 1,273,700;G2 的a1,b1,c1分别为0.020 3,264,580。两台机组的污染物排放系数以及环境折算成本系数如表1 所示。电力系统对VPP 的电费支付遵循分时电价机制[16]。 以1 d 为调度时间,以0.5 h 为一个调度时段,对VPP 制定运行计划以满足电力系统对出力计划的要求。
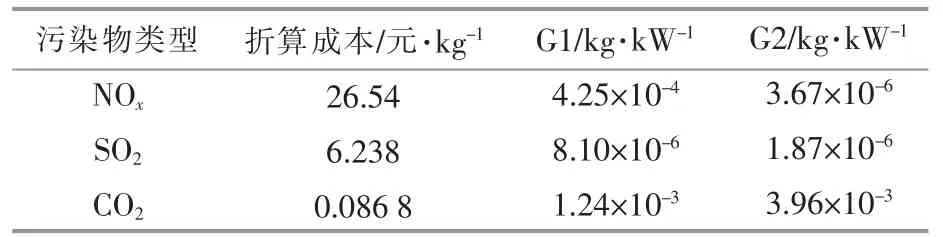
表1 环境折算成本系数与污染物排放系数Table 1 Environmental conversion cost coefficient and pollutant emission coefficient

图1 风光出力的区间不确定性以及系统要求VPP 出力曲线Fig.1 Interval uncertainty of wind power output and power output curve of virtual power plant required by the system
图1 为VPP 调度时间范围内典型运行日下1 d 各时段分布式风电和光伏出力预测基准功率区间不确定性以及电力系统对VPP 要求的出力计划。
3.2 鲁棒优化运行方案及其分析
运行所建立的鲁棒优化模型,得到的VPP 在1 d 之内的最优经济调度计划如图2 和图3 所示,其中,图2 为机组出力及储能充放电计划,图3 为机组启停计划。 事实上,在该运行方案下,分布式风电和分布式光伏出力全额消纳, 消纳率达到了100%,没有出现弃风弃光现象。
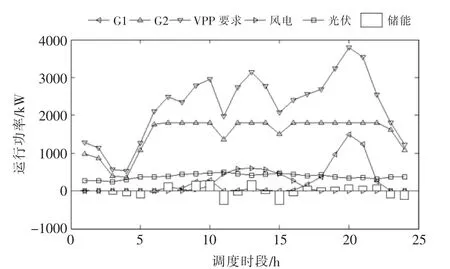
图2 VPP 典型调度日内运行计划Fig.2 Operation plan of virtual power plant on a typical dispatching day
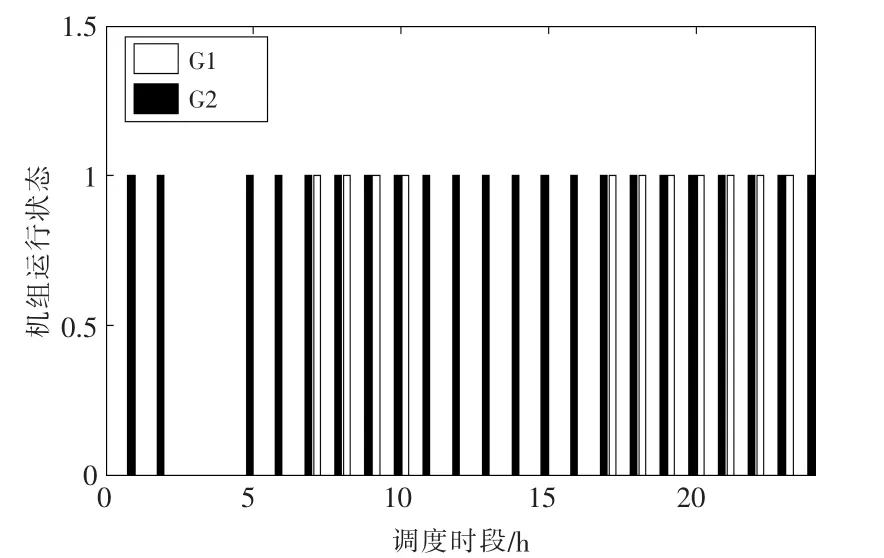
图3 VPP 典型运行日内各时段机组组合计划Fig.3 Unit commitment plan of virtual power plant on a typical operation days
从图2 和图3 中可以看出,VPP 通过合理地安排系统内机组的组合计划以及出力计划, 配合储能充放电出力,使得VPP 满足电力系统输出功率的要求。 在第1~4 时段,VPP 要求出力水平处于低谷,VPP 安排燃料成本相对较为低廉的G2发电,在满足VPP 出力曲线的同时,将多余的电能通过储能设备进行存储, 为后续的放电过程做好准备。 在第5~16 时段,VPP 要求出力水平较高,VPP 主要通过G2 的出力结合可再生能源发电出力基本上能够满足VPP 出力曲线的要求。 在阶段性的高峰时段,VPP 控制储能设备处于放电状态,以便对出力曲线进行调节。在个别可再生能源出力和G2 无法满足VPP 出力要求时,VPP 不得不增开G1,并尽可能安排G1 的发电时段较为连续集中, 从而降低机组组合成本。 在第17~23时段,外界电力系统达到负荷高峰,则进一步增加了对VPP 要求的出力功率。 在该时段,分布式风电和分布式光伏出力较低,VPP 在G2 运行的基础上增开G1,并令储能放电以满足出力要求。 燃料成本相对较低的G2 处于满发状态,G1 和储能则对VPP 出力曲线进行有效调节。在该运行计划下,VPP 的综合运行成本为52 013.69 元,在发电经济效益为76 852.47 元的情况下,发电净收益为24 838.78 元。
事实上,以上VPP 运行计划是基于鲁棒优化理论得到的, 即考虑到系统决策者和自然决策者的博弈达到均衡, 能够面对自然决策者采用对VPP 最不利策略下实现最优运行。 自然决策者的策略如图4 所示。
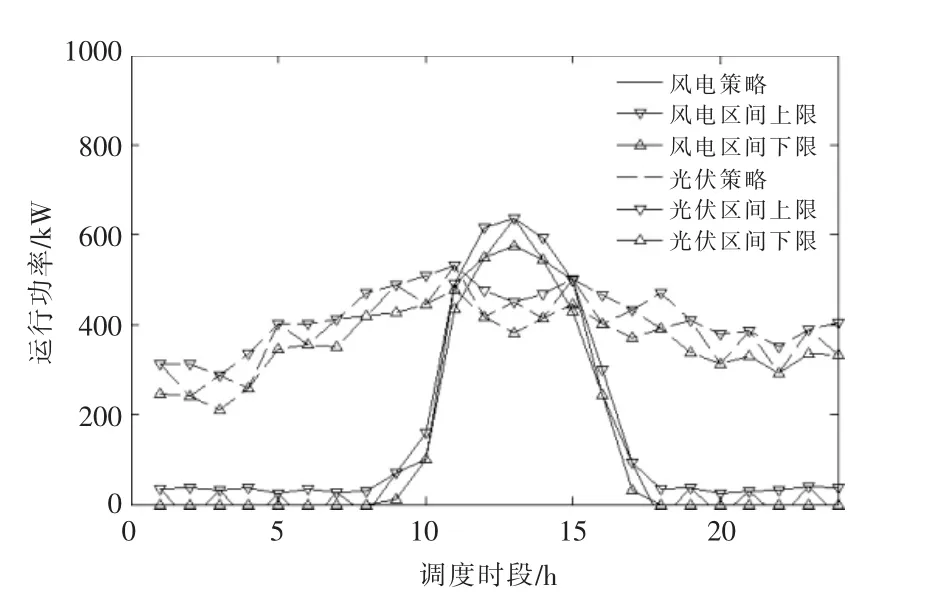
图4 鲁棒优化框架下自然决策者的风电光伏出力策略Fig.4 Wind power photovoltaic output strategy of natural decision maker under robust optimization framework
从图4 中可以看出, 自然决策者的策略通过安排分布式风电和分布式光伏出力的较大波动增加VPP 频繁启停机组的可能性,从而增加系统运行成本。
VPP 通过先进的智能电网技术实现了对电力系统中多个发电资源的整合, 能够统筹协调不同设备的运行功率实现经济效益的最优, 有利于电力系统降低运行成本。为了对比VPP 和传统的按发电容量进行分配功率的方式,在同样的VPP 出力要求下, 分别在两种方式下制定各个发电设备的出力计划并得到综合运行成本对比,见表2。
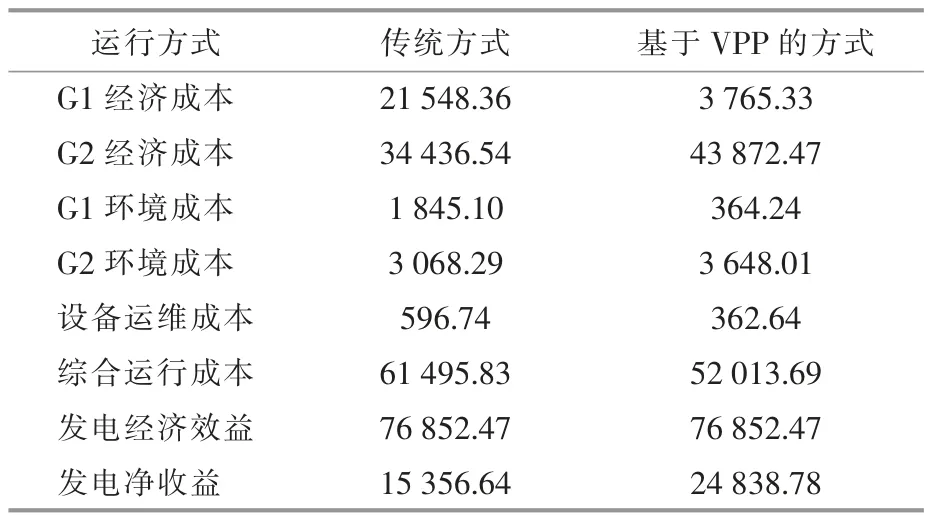
表2 两种方式下VPP 运行经济指标对比Table 2 Comparison of economic indexes of virtual power plant under two modes 元
从表2 中可以看出: 与传统的各个发电资源进行调度的方式相比,VPP 方式下系统1 d 的综合运行成本从61 495.83 元下降到了52 013.69元;在相同的发电经济效益情况下,发电净收益从15 356.64 元上升到了24 838.78 元, 具有较为显著的经济效益。
为了验证本文所建立的模型相比于传统的VPP 最优经济调度模型的优势, 设置两种运行场景分别进行优化。其中:场景一为采用传统的优化方法,不考虑风光出力的不确定性;场景二为基于本文所建立的VPP 最优经济调度鲁棒优化模型。两种场景下VPP 运行指标对比如表3 所示。
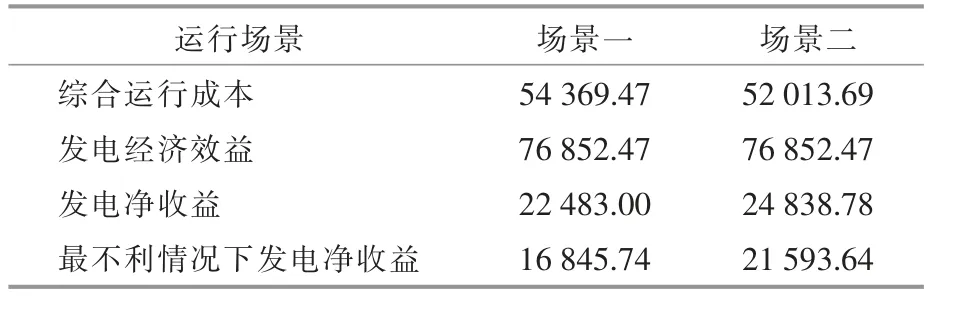
表3 两种场景下VPP 运行指标Table 3 Operation indexes of virtual power plant under two scenarios 元
从表3 中可以看出,场景二相比于场景一,由于考虑了风光出力的不确定性, 系统的运行方案更加具备适应性,因此综合运行成本更低、发电净收益更高。 同时, 采用鲁棒优化理论构建的VPP经济调度模型使得运行方案能够应对风光出力最不利的情况, 该情况下场景二的发电净收益显著高于场景一,增加幅度达到了28.18%。
4 结论
①本文采用鲁棒优化理论建立了VPP 最优经济调度模型,并基于该模型针对典型VPP 制定机组组合计划和发电运行计划。
②仿真算例表明, 相比于传统的分布式发电资源调度方式,基于VPP 的最优经济调度模型能够降低系统综合运行成本,提升发电净收益。
③采用鲁棒优化理论建立VPP 最优经济调度模型,相比于传统的不考虑不确定性的方式,系统的运行计划具备更优的适应性和鲁棒性。
