基于马氏距离相似度量的光伏功率超短期预测方法的研究

杨 茂， 冯 帆

（东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室， 吉林 吉林 132012）

0 引言

受昼夜更替和天气不确定性的影响， 光伏功率具有随机性、间歇性等特点。 因此，大规模的光伏发电并网会对电力系统的稳定运行产生影响。 准确预测光伏功率可以有效提高光伏发电并网时电网的稳定性、 增强电网消纳光电能力、减小由于弃光限电造成的经济损失、提高运营管理效率[1]。

光伏功率预测方法大致分为两种，一种为基于持续法及晴空预测模型的基础预测方法，另一种为基于云图及数据驱动的超短期预测方法。 文献[2]采用机器学习方法对大气气溶胶光学厚度进行估计，同时，修正了光伏电池面板接收的太阳辐射强度数据，提高光伏功率的超短期预测精度。 文献[3]通过对地基云图进行处理与分析，实现对云团未来运动状况的预估，进而预测太阳辐射强度和光伏功率，此方法在一定程度上提高了预测精度，但地基云图仪和天空成像仪造价较为昂贵，不易普及应用。 此外，还有基于时间序列、神经网络算法、支持向量机（SVM）算法、深度学习预测算法等的预测方法[4]～[8]。 同时，基于相似日的光伏出力预测方法也很常见。

寻找相似日的方法中，基于欧氏距离寻找的方法较为普遍， 但通过此方法得到的相似日和预测日的各气象数据与光伏功率的拟合度较低，不能有效提高预测精度。

本文提出了一种基于马氏距离相似度量的光伏功率超短期预测方法。首先，本文采用Elkan Kmeans 聚类分析方法对天气类型进行划分；然后，计算各气象因素与光伏功率在不同天气类型下的灰色关联度， 并取灰色关联度相对较高的3 个气象因素作为影响光伏功率的主要因素；其次，基于马氏距离寻找与预测日满足一定阈值要求的样本日作为相似日；最后，将相似日的光伏功率作为预测模型的训练集， 对预测日的光伏功率进行超短期预测， 并通过模拟结果验证了本文方法的有效性。

不断刷新自身时尚形象的青岛啤酒，每切入一个细分市场，都紧扣年轻人多元化、个性化的需求，于是青啤与年轻人站到了一起。

1 天气类型的划分

1.1 光伏功率的变化曲线

由于昼夜交替变换， 光伏功率具有明显的周期性特点。但在不同天气类型下，光伏功率的变化趋势各不相同。 本文根据每日光伏功率的变化趋势，将天气类型分为3 类，分别为晴天、多云天气和阴雨天气（不考虑一天内出现不同天气类型转换的情况）。 图1 为不同天气类型下，光伏功率随时间的变化曲线。

图1 不同天气类型下，光伏功率随时间的变化曲线Fig.1 Variation curve of PV power with time under different weather types

由图1 可知，晴天时，光伏功率曲线先平缓上升再平缓下降，波动性较小，这是由于光伏电站出力主要受日升日落的影响；多云天气时，光伏电站仍有明显出力，但与晴天相比，光伏电站整体出力偏小，且存在较多骤降点，波动性较强，这是由于光伏电站出力虽然主要还受日升日落的影响，但同时也受云层的影响，云层遮挡太阳时，光伏电站接收太阳辐照强度变小，造成光伏电站整体出力偏小，从而出现骤降点；阴雨天气时，光伏电站整体出力偏低，且有一定的波动性，这是由于阴雨天气时，云量和雨量的变化程度较大，光伏电站接收的太阳辐照强度较小，此时，光伏电站出力受日升日落的影响并不显著。 综上可知，不同天气类型对光伏电站出力的影响不同，存在一定的波动性。

1.2 Elkan K-means 聚类分析方法

本文利用Elkan K-means 聚类分析方法对天气类型进行划分，Elkan K-means 聚类分析方法是对K-means 聚类算法中的距离计算过程优化后得到的聚类方法， 其主要算法流程和K-means聚类算法类似：首先，输入样本数据集D，确定聚类数k 及最大迭代次数N， 并随机选择k 个初始聚类中心{μ1，μ2，...，μk}，便形成了k 个簇；然后，划分出λ 个初始化簇Cλ=Φ （其中，λ=1，2，...，k；Cλ为第λ 个初始簇的集合；Φ 表示空集），计算样本xj（j=1，2，...，k）与各个聚类中心μi之间的距离d（xj，μi）。 d（xj，μi）的计算式为

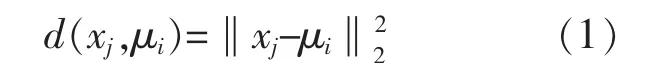
其次，根据d（xj，μi）将样本xj划分到与其距离最近的聚类中心所属的簇中；最后，计算新的聚类集的聚类中心，进行下一次迭代，直到聚类中心不再变化或者达到最大的迭代次数为止[9]。

Elkan K-means 聚类分析方法的优化目标为最小化平方误差J。 J 的计算式为

式中：μi为第i 个聚类中心；n 为在第i 个聚类中样本的个数；rji为最小化平方误差J 每一项的计算系数，符合0～1 分布。

rji的表达式为

在利用Elkan K-means 聚类分析方法过程中， 若样本为xj，2 个类型的聚类中心分别为μp，μq，这2 个聚类中心的距离记为d（μp，μq），样本xj到2 个聚类中心的距离分别为d（xj，μp），d（xj，μq），若2d（xj，μp）≤d（μp，μq），则 表 明d（xj，μp）≤d（xj，μq），此时，无须计算d（xj，μq）。

在理工类院校的专业学习中，C语言是计算机及其相关专业的基础学科，其学习效果直接影响更为专业的学习课程。院校要高度重视C语言的学习，在课程设置、教师选用、学习效果考核等方面强化投入和管理，但总体感觉成效并不理想。C语言是一种非常抽象且对逻辑性要求特别高的课程，教学难度非常大，为此，有必要对教学模式进行改革，从根本上提升其教学质量。

（3）可以使物流企业的设备的更新换代速度更快，因为营业税改成增值税后，购买机器设备和交通运输工具等的进项税额就可以凭票抵扣，然后物流公司就可以安心地购买新机器设备了，不用担心税负沉重，因为抵扣进项还可以使企业当年少交增值税，所以最终的结果就是企业可以不断更换新的工具和机器使生产运作效率更优。

2 基于马氏距离的相似日选择方法

2.1 光伏功率的主要影响因素

结合数据库技术与应用课程特点及教学体验，按照“案例导向、项目驱动”的教学方法[7]，选择专题项目作为案例，通过项目案例将数据库技术与学科专业关联起来，将理论学习与实践训练融为一体。课堂教学按教学线进行，以讲解基础知识为基石，介绍项目案例为主，讨论为辅。实践教学按实践线进行，以项目开发为主，模拟企业的项目管理和开发过程，以项目开发带动数据库课程的理论学习，每一个子项目按照“任务实现→问题分析→知识储备→项目实践”的模式，使学生可以循序渐进地学习数据库的知识和技能，更好地掌握所学内容，并与学科专业相融合。

2.2 灰色关联度计算

合格率r2的计算式为

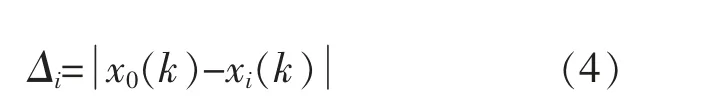
计算出求差序列Δi的两极最大值和最小值，分别记为MAX=max Δi（max），MIN=min Δi（min）。则关联系数γoi（k）的计算式为

2017年，黑龙江省建设高效节水灌溉工程6.75×104 hm2、推广节水控制灌溉技术1.8×105 hm2。工业以高耗水行业为重点，大力实施节水技术升级和系统改造。推广非常规水源开发利用，切实推进城市供水管网漏失改造。加强对省市县三级重点用水户的监控管理，推行非居民用水超计划、超定额累进加价制度。推进中小学生节水教育社会实践活动，推进省级机关节水型单位建设。

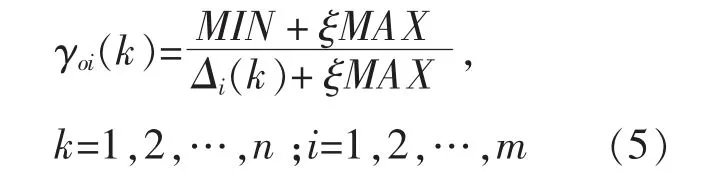
式中：ξ 为灰色关联度的分辨系数，取0.5；m 为参考序列、比较序列中xi（k）或x0（k）中元素的个数。

由γoi（k）可得到参考序列与比较序列的灰色关联度γoi。 γoi的计算式为

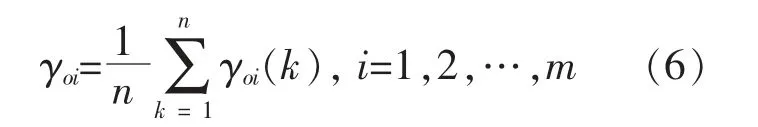
灰色关联度的值越大， 代表气象因素与光伏功率的相关性越高。 各天气类型下的主要气象因素与光伏功率的灰色关联度如图2 所示。

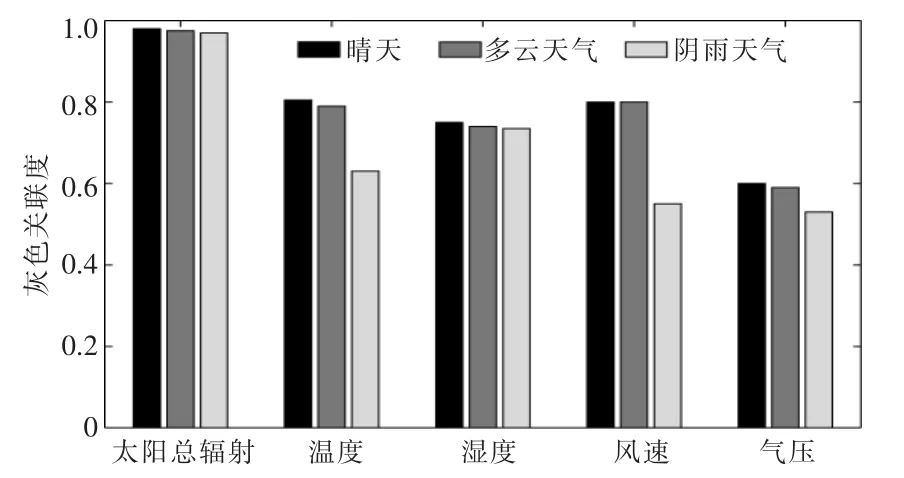
图2 各天气类型下的主要气象因素与光伏功率的灰色关联度Fig.2 Gray correlation degree between main meteorological factors and PV power under various weather types

由图2 可知，晴天和多云天气时，影响光伏功率的主要气象因素为太阳总辐射量、温度、风速；阴雨天时， 影响光伏功率的主要气象因素为太阳总辐射量、温度、湿度。

2.3 基于马氏距离的相似日选取方法

欧氏距离为各变量与变量平均值之间的几何距离，该方法没有考虑变量之间的相关性。为解决这一问题， 印度著名统计学家马哈拉诺比斯提出了一种基于多元统计的马氏距离计算方法， 马氏距离的计算是建立在多元正态分布理论基础之上，该方法考虑了多种因素之间的相互作用，不仅可以计算出2 个未知样本集之间的相似度， 还可以进行多元样本分析[12]。

式中：μx=E（xi）；μy=E（yi）。

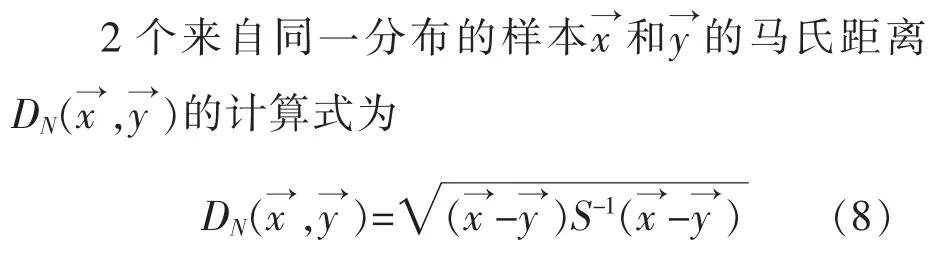
最后， 选取与预测日距离满足一定阈值要求的样本日作为相似日。

3 光伏功率超短期预测模型

为了验证本文方法的有效性， 本文将基于马氏距离和欧氏距离这2 种方法得到的相似日的光伏功率分别输入到极限学习机（ELM） 预测模型中，对同一时段的光伏功率进行超短期预测，并对基于马氏距离和欧氏距离方法得到的预测结果进行比较。

3.1 预测模型的介绍

ELM 是一种单隐层前馈神经网络，ELM 通过随机确定输入权重和偏差，用于分析、计算输出权重。 极限学习机可对难以求解的非线性问题进行优化，如将计算输入权重、隐层偏差、输出权重的过程转化为求解最优输出权重的过程以简化运算[13]。

ELM 算法具有在学习过程中，无须调整隐含层节点参数和输入层至隐含层的特征映射的特点，还具有可以随机或人为给定的特点。由于仅须求解输出权重， 因此，ELM 在本质上是线性参数模式，其算法易实现全局收敛[14]。

若ELM 的学习数据样本为{xj，tj}M，xj和tj分别表示模型的输入、输出数据，且xj，tj均属于实数集R，则单隐层神经网络的表达式为

式中：Kcon为隐含层节点数；βi为输出权重；g 为激活函数；wi为输入神经元和第i 个隐层神经元之间的连接权值；xj为数据样本；bi为第i 个隐含层神经元的偏差补偿值；tj为输出向量；M 为样本总数。

设T 为输出向量的矩阵形式， β为输出权重向量，则可以得到输出向量的表达式，即T=Hβ的形式，其中，H 为ELM 神经网络的隐含层输出矩阵。

H 的矩阵式为

ELM 模型的训练过程：首先，确定神经元个数，随机分配节点参数；然后，计算隐含层的第M行第K 列的输出矩阵；最后，求解误差函数最小的输出权重。

3.2 评价指标

预测结果的均方根误差RMSE 的计算式为

预测准确率r1的计算式为

王老师：听起来似乎有一些道理。凭借良好语感和模仿，学生在一开始的确不会出现太多的病句，因为他们基本上都是在套用句式。但即便他们说对了、写对了，他们也不知道“为什么对”，而只是“我感觉对”。脱离模仿造句阶段后，学生最终还是要依靠理性来分析句子而不只是凭感觉来判断。因此，在语感培养达到一定基础之后，第二个阶段就需要补充语法知识，这样才能帮助学生在交流时做到“准确地表述”，而不仅仅只是“表述”。遗憾的是，我们现在主张“淡化语法”，让学生的语言学习永远处在“跟着感觉走”的状态，导致现在学生的交流、表达中存在大量的语病，这反而影响了学生的表达热情。

式中：PMi为预测光伏功率；PPi为实际光伏功率；Np为预测点的个数；Cap为光伏电站开机容量。

本文采用相似日的光伏功率作为预测模型的训练集[10]。 输入的气象数据与输出的光伏功率相关性越强，表明相似日的选择效果越好。 因此，在选择相似日时， 为了避免选择结果受一些次要气象因素的影响，本文在不同天气类型下，分别选择了主要影响因素。 具体方法：在各天气类型下，分别计算太阳总辐射量、温度、湿度、风速、大气压强等气象因素与光伏功率之间的灰色关联度， 并选取灰色关联度较大的3 个气象因素作为对应天气类型下的主要影响因素[11]。

将上述2 组相似日的光伏功率分别输入到ELM 训练模型中， 对光伏功率进行超短期预测，并比较预测结果。 以此探究相似日选取的准确性对预测结果的影响。

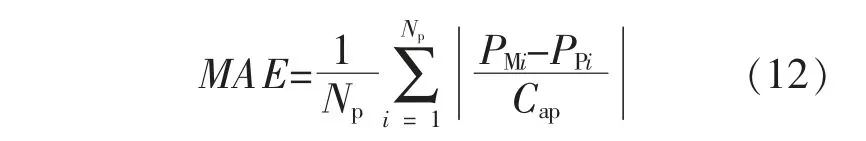
在路面施工中会使用到较多的大型机械设备，例如摊铺机、装载车等等，这些大型的机械设备需要在施工现场进行交叉作业，设备管理的难度增大，如果调度出现问题，可能会引发交通事故。

将气象数据、光伏功率进行归一化处理后，本文以光伏功率作为参考序列X0={x0（1），x0（2），...，x0（n）}，以 各 气 象 数 据 作 为 比 较 序 列Xi={xi（1），xi（2），...，xi（n）}，得到两者的求差序列Δi的计算式为

式中：Bk为符合0～1 分布的随机变量。

Bk的表达式为

4 算例分析

本文以常晖红星光伏电站2018 年1 月1日-2018 年8 月31 日的实测光伏功率以及气象数据作为样本，数据采样时间间隔为15 min，该电站的装机容量为30 MW。 分别选取8 月15 日（阴雨天）、8 月26 日（多云天气）和8 月30 日（晴天）作为预测日， 对各时段的光伏功率进行超短期预测时， 样本为2018 年1 月1 日-2018 年8 月31日常晖红星光伏电站各参数的实测数据， 取值时间间隔为15 min。 模拟过程中的输入数据为相似日和预测日光伏电站发电功率实测数据。

本文以晴天为例，选择太阳总辐射量、温度、风速为主要影响因素， 分别求得各样本日和预测日的马氏距离和欧氏距离， 选择与预测日距离最近的34 个样本日作为相似日。分别在以上2 组相似日中随机选取7 d，并绘制光伏功率散点图。

所谓的“三分法”是指经济后果观存在零经济后果、正经济后果、和负经济后果。零经济后果实质上就是“信息中立”，其内涵是会计信息与所反映的客观经济事实的价值运动相一致，不带有任何偏见，客观独立公正。正经济后果是指会计信息系统充分考虑利益相关者的信息需求，该信息具备相关性、可靠性，有利于利益相关者的投资及其相关决策，能够帮助他们作出科学合理的决策，维护他们的利益；而负经济后果是指会计信息扭曲了企业的财务状况、经营成果及其现金流量状况，误导利益相关者的投资决策，导致其投资失当，造成资源浪费。

图3 为基于欧氏距离得到的相似日光伏功率散点图。

与K-means 聚类算法相比，Elkan K-means聚类分析方法在不影响聚类效果的前提下， 利用了三角形两边之和大于第三边， 两边之差小于第三边的性质，在求J 的极小值的过程中，计算过程更为简单，同时也减少了迭代次数，提高了聚类的速度。

随着我国的食品安全标准与国际标准不断接轨，越来越多的食品企业在推进食品安全体系建设与完善的路上已越走越稳。而现阶段奖惩分明的市场环境，也让食品行业企业不敢、不想、不愿“犯错”。种种向好态势，让我国食品安全未来可期。

图4 为基于马氏距离得到的相似日光伏功率散点图。

由图3，4 可知， 基于欧氏距离求得的各相似日的光伏功率的分布比较分散， 说明其和预测日的光伏功率分布相似度较低。 而基于马氏距离求得的相似日的光伏功率散点集中分布在预测日光伏功率曲线附近，与前者相比，能够更加准确地反应预测日的光伏功率特征。

其中草菇料酒和茶树菇料酒中总糖含量偏高，茶树菇料酒中的总酸含量最高，茶树菇料酒、平菇料酒、海鲜菇料酒和草菇料酒的氨基酸态氮含量超过了1 g/L，酒精度较高的是杏鲍菇料酒和灰树花料酒，香菇料酒的非糖固形物含量较高，草菇料酒的pH值含量较高。由此可见，各食用菌同料酒共同发酵其营养物质不同，其对应的理化指标表现的风味活性成分的含量也不同。

为了验证马氏距离相似度量的有效性， 本文基于上述2 种方法寻找8 月26 日-31 日这10 个相似日， 并统计各相似日和预测日的光伏功率的均方根误差及其平均值。 各相似日和预测日的光伏功率的均方根误差的平均值如表1 所示。 由表1 可知，除28 日外，其余5 d 基于马氏距离相似度量得到的各相似日和预测日的光伏功率的均方根误差的平均值均小于基于欧氏距离得到的。 8 月29 日，2 种方法的均方根误差的平均值相差最大，为4.39%；8 月27 日，2 种方法的均方根误差的平均值相差最小，为0.54%。 由此验证，基于马氏距离相似度量得到的相似日的方法效果更优， 获得的相似日和预测日的光伏功率的相似程度更高。

20例患者均接受MRA与MRI检查，应用日本东芝1.5T超导磁共振扫描仪，扫描参数设置：3D TOF MRA方法，其中TR=42ms，TE=8ms，Ta=35°，或者采用3DPC方法，其中TR=24ms，TE=11ms，Ta=15°，层厚：1mm，行连续扫描。其中原始图像应用最高强度的投影MIP方法实施自动化处理，重建后获得患者三维血管图像。接受MRI检查患者均在其头部MRI实施平扫基础上采取3D血管成像扫描检查，其轴位显示野：20cm×20cm。

平均绝对误差MAE 的计算式为

在预测过程中，为了更加客观、全面地考量预测结果，须要排除一些干扰因素。 一方面，无日照（光伏功率为零）时对预测结果的影响较小，因此，本文只对有日照时段进行预测；另一方面，预测时段选取不同，预测结果不同，因此，本文逐点滑动地选取32 个时段分别进行预测。

图5 为8 月30 日（晴天）8：00-12：00 光伏功率的预测结果。

本文采用改进神经网络PID控制器研究车辆转向控制系统,建立车辆转向机构运动简图模型,推导车辆摆动角速度与转角之间关系式.修改传统PID控制器,添加人工神经网络模型,引用改进PSO对PID控制器参数进行优化和在线调整,在Matlab软件中对优化后人工神经网络PID控制器参数进行仿真,并且与PID控制器进行比较.仿真曲线显示:常规工况路面,PID控制器和改进人工神经网络PID控制器都能很好地实现摆动角速度跟踪任务,但是对于复杂工况路面,改进人工神经网络PID控制明显优于PID控制器,能够快速、精确地实现跟踪任务,提高车辆行驶的稳定性.

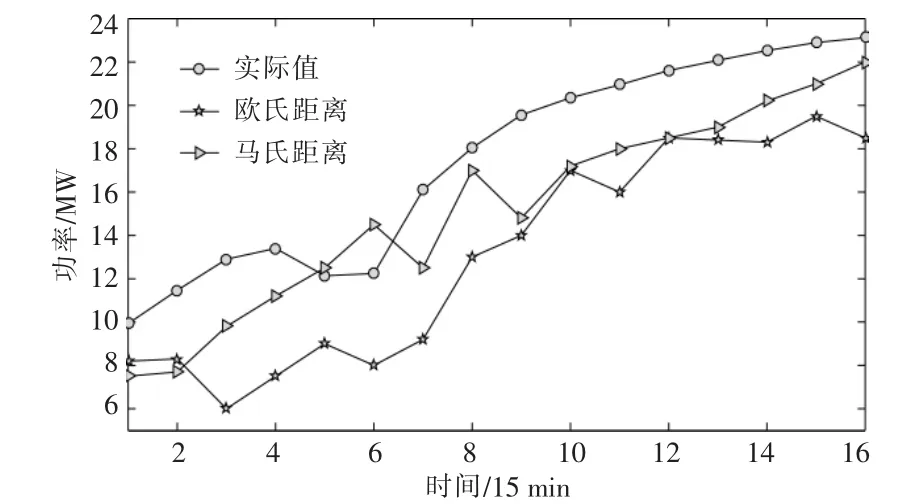
图5 8 月30 日（晴天）8：00-12：00 光伏功率的预测结果Fig.5 Forecast results of PV power on August 30 （sunny day） from 8：00-12：00

由图5 可知，本文方法预测值更加接近真实值。 为了直观地反应预测结果，本文分别采用均方根误差、平均绝对误差、准确率和合格率4 个指标评价预测效果，表2 为基于马氏距离和欧氏距离相似度量的光伏功率超短期预测的各评价指标。

表2 基于马氏距离和欧氏距离相似度量的光伏功率超短期预测的各评价指标Table 2 Evaluation indicators for ultra-short-term prediction of PV power based on Mahalanobis distance and Euclidean distance %

由表2 可知，基于马氏距离相似度量得到的相似日的光伏功率作为预测模型的输入时，得到的预测效果更好， 其中均方根误差降低了2.29%，平均绝对误差降低了1.30%，准确率提高了2.29%。 晴天，逐点滑动32 次对光伏功率进行超短期预测， 预测结果的均方根误差和平均绝对误差结果如图6 所示。

图6 晴天，逐点滑动32 次对光伏功率进行超短期预测，预测结果的均方根误差和平均绝对误差结果Fig.6 On a sunny day, the results of the root mean square error and the average absolute error of the ultra-short-term prediction of PV power by sliding 32 times point by point

由图6 可知， 基于本文方法对光伏功率进行超短期预测时， 得到的各误差值均较小， 由此可知，本文方法对晴天有日照的各时段均适用，可减小预测误差，提高了预测准确率。

基于本文方法， 分别统计了各天气类型下预测结果的均方根误差和平均绝对误差， 统计结果见表3。

表3 各天气类型下预测结果的均方根误差和平均绝对误差Table 3 Root mean square error and average absolute error of forecast results under each weather type %

由表3 可知，各天气类型下，当预测模型的输入分别为基于马氏距离或欧氏距离相似度量得到的相似日的光伏功率时， 前者预测误差均小于后者， 由此证明了基于马氏距离相似度量得到的相似日的光伏功率作为预测模型的训练集时， 可以提高预测精度。由表3 还可以看出，多云天气和晴天的预测误差较小，这是由多云天气和晴天，光伏功率趋势性、规律性较强导致的；而阴雨天气的预测误差较大， 这是由阴雨天气， 光伏功率波动剧烈，时常出现陡升或陡降的波动导致的。

这样就可以理解:本为表示味觉属性状态的“甘苦”为什么会用于借指美好的处境和艰苦的处境，也可以指称在工作或经历中体会到的滋味,多偏指苦的一面；本为汉字构造部件的“丘八”为什么旧时被用于称呼士兵了,八十八岁为什么会被称为“米寿”,一百零八岁为什么会被称为“茶寿”了。

5 结论

本文提出一种基于马氏距离相似度量得到的相似日并进行光伏功率超短期预测的方法， 通过提高相似日和预测日的光伏功率的相似度来提高超短期预测的精度， 并通过算例分析可以得到以下结论。

①不同天气类型下， 影响光伏功率的主要气象因素不同。为避免其他次要因素的干扰，本文通过计算灰色关联度衡量各气象因素对光伏功率的影响程度。 在晴天和多云天气的主要影响因素为太阳总辐射量、温度和风速；阴雨天气的主要影响因素为太阳总辐射量、温度和湿度。

②由于马氏距离是建立在多元正态分布理论基础之上， 并且光伏功率受到多种因素影响，因此， 基于马氏距离相似度量得到的相似日的光伏功率散点更加集中在预测日的光伏功率曲线附近，与预测日的相似度较高。

③预测模型输入的训练样本与预测日的相似程度对输出的预测结果会产生一定的影响， 根据本文方法得到的相似日的光伏功率作为预测模型的训练集，提高了光伏功率超短期预测的精度，减小了预测误差。