“六连环状教学模型”在高中数学教学中的运用——以《等差数列的前n项和公式》为例

◎ 黄美珍

“六连环状教学模型”是在对学生学习内容、学习方式、学习过程和学习结果等方面研究的基础上，在尊重和利用学生的认知发展规律的条件下，以学习过程为中心、以学生的学习结果为最终目标而构建的教学框架[1]。该教学模型包括“启动、自学、交流、展示、运用、总结”六个教学环节。将以《等差数列的前n项和公式》一课为例，阐述这种新型的教学模式在数学课堂教学中的应用。

一、启动：创设情境、激发动机

启动，是指学生状态的启动，激发学生学习的好奇心和兴趣，让学生以尽快速度投入本节课内容的学习。启动所用的时间不宜太长，可以以学生已有的相关背景知识为课堂的开始，甚至可以根据教学内容的需要创设活动场景，从而开启本节课的学习。

以《等差数列的前n项和公式》这一内容为例，教师可创设以下情景，进入课堂的启动环节。

据说，200多年前，高斯的算术老师提出了下面的问题：

有一次，老师与高斯去买铅笔，在商店发现了一个堆放铅笔的V形架，V形架的最下面一层放一支铅笔，往上每一层都比它下面一层多放一支，最上面一层放100 支。老师问：高斯，你知道这个V形架上共放着多少支铅笔吗[2]？

高斯的算法：(1+100)+(2+99)+(3+98)+…+(50+51)=101×50=5050

【设计意图】通过回顾历史中高斯的小故事，激发学生的好奇心和学习兴趣，调动学生学习积极性，为本节课的学习奠定愉快的学习氛围，从而开启本节课的学习。

二、自学：自主探究、验证猜想

自学，是指学生根据教师预设的问题，对本节课的学习内容进行自主探究。强调的是学生对知识的主动探索与主动发现，最终化为自己的知识。所以，教师在备课的时候，要根据本节课的教学内容，创设好问题，便于学生自主探究。

问题1：为什么(1+100)=(2+99)=(3+98)=…=(50+51)呢？这是巧合吗？试从数列角度给出解释。

问题2：你能用上述方法计算1+2+3+…+101吗？

问题3：你能计算1+2+3+…+n吗？

Sn=1+2+3+…+n，Sn=n+(n-1) +(n-2)+…+1

将上述两式相加，得

2Sn=(n+1)+[(n-1)+2]+[(n-2)+3]+…+(n+1)=(n+1) +(n+1) +(n+1)+…+(n+1)=n(n+1)

所以Sn=1+2+3+…+n=

【设计意图】通过问题引导以及学生小组合作探究的方式激发学生的学习思维，培养学生合作探究能力和归纳分析能力，发展学生数学抽象和数学建模的核心素养。

三、交流：合作交流、归纳总结

交流是指学生之间交流自主学习的成果。教师在课堂上是引导者，学生才是课堂的主体，教学活动的主要参与者，要倡导发展学生的自主学习和合作精神。教师可以适时组织学生进行小组合作学习，让学生亲自参与到探索新知识的过程中，提高学生学习的积极性。

问题4.上述方法的妙处在哪里？这种方法是否适用于求所有等差数列{an}的前n项和？

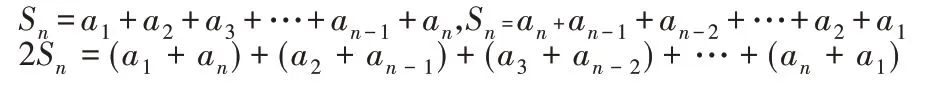
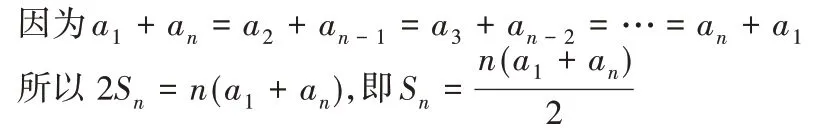
四、展示：知识总结、加深理解

展示，是指学生根据前面的自主探究以及合作交流，展示本节课的学习内容。教师可先由学生进行展示，再进行补充。通过这一环节，学生可以在积极的状态中接受新知识，突出学生的主体地位。

归纳总结：等差数列的前n项和公式：Sn=和Sn=

五、运用：例题讲解、巩固训练

运用，就是要学以致用，把建构的知识、强化的技能与多个知识点联合起来，解决实际的问题，完成相关任务，实现再创造的过程。

例1.已知数列{an} 是等差数列，

1.若a1=7，a50=101，求S50；2.若a1=14.5，d=0.7，an=32，求Sn；总结：

(1)利用基本量求值：等差数列中五个基本量，知三求二，利用公式列出基本量a1和d的方程组，解出a1和d，便可解决问题。

(2)结合等差数列的性质解题。例2.已知一个等差数列{an}前10 项的和是310，前20 项的和是1220。由这些条件能确定这个等差数列的首项和公差吗？

【设计意图】通过设置具有代表性、覆盖性强、梯度性好、难度适中的例题，采用教师讲解、学生思考的方式进行，加深学生对等差数列求和公式的理解，发展学生的学科素养。

课堂训练

设Sn是等差数列{an}的前n项和，若a1+a3+a5=3，则S5=____

已知等差数列{an}中，已知d=2，n=15，an=-10，求a1和Sn。

已知等差数列{an}中，已知a1=20，an=54，Sn=999，求n和d。

【设计意图】通过设置有梯度的练习，满足了不同层次学生的要求。通过学生解决问题，发展学生数学运算、逻辑推理、直观想象、数学建模的核心素养。

六、总结：课堂小结、巩固重点

总结，就是在完成课堂教学内容后，对本节课知识和学习方法进行归纳总结，形成知识网络体系。这一环节可以帮助学生对本节课知识有梳理升华的效果，也能让教师从宏观上更好地把握课堂内容，对今后教学有参考的作用。

“六连环状教学模型”下的教学课堂，旨在实现课堂的“高质量”，让教师有高质量的教学过程，让学生有高质量的学习结果。通过“六连环状教学模型”设置《等差数列的前n项和公式》的教学，充分尊重和利用了学生的认知发展规律，优化了本节课的学习环境。重视与学生的交流和互动，实现了学生的主动学习和有效学习，使学生的学习效果和教师的教学效果更加凸显。