基于代理模型的大尺寸矩形截面超声变幅杆的优化设计∗

（昆明船舶设备研究试验中心 昆明 650051）

1 引言

超声变幅杆是超声系统的重要组成部分，其主要作用是传递并聚集能量。设计变幅杆时，要求其谐振频率尽可能接近超声系统的工作频率。当变幅杆的横截面尺寸远小于波长时，可忽略杆横向振动的影响，其设计主要基于一维纵向振动理论；当变幅杆的横向尺寸大于1/4波长时，由于泊松效应，杆的横向振动较大，若基于一维纵向振动理论设计，变幅杆谐振频率的偏差较大［1］。关于大尺寸矩形截面变幅杆的设计，相关研究主要是基于横、纵耦合振动理论将变幅杆谐振频率修正到系统工作频率附近［2～4］。然而，大尺寸矩形截面变幅杆在实际应用中，仅修正谐振频率远远不够，还需要抑制其横向振动，使变幅杆输出端振幅分布更均匀才能适应实际使用需求。实际应用中，为了抑制矩形截面变幅杆宽度方向上的横向振动，会根据经验在变幅杆上开一些细长窄缝［5］。细长窄缝的增加会改变变幅杆的谐振频率和振动模态，而通过解析法求解变幅杆窄缝的结构参数与变幅杆谐振频率的关系较为困难。目前，关于窄缝结构参数对变幅杆谐振频率的影响，鲜有相关研究。

本文考虑通过在变幅杆上增加窄缝的方式，在抑制大尺寸矩形截面变幅杆横向振动的同时，修正其谐振频率。先基于一维纵振理论设计较为常见的大尺寸矩形截面指数形变幅杆。再采用三种方法构建根据窄缝的结构参数预测变幅杆纵振谐振频率的代理模型。接着，评价模型精度并选取精度较高的模型，结合遗传算法对变幅杆窄缝结构参数进行优化。最后，通过仿真实验验证优化结果的正确性。

2 变幅杆设计

2.1 设计理论和设计参数

变幅杆一维纵向简谐振动方程如下：

式中，x为沿杆长度的质点坐标值；ξ（x）为质点位移函数；k为圆波数；S（x）为变幅杆的截面积函数。本文以工程上较为常用的指数形变幅杆为例进行分析，指数形变幅杆的截面积函数为

变幅杆采用7075铝合金材质，大端（输入端）尺寸为27mm×80mm，小端（输出端）尺寸为3mm×80mm，系统工作频率和输入振幅分别为20KHz和7μm。变幅杆的设计目标为通过在矩形截面变幅杆宽度方向上增加两个窄缝，使其纵向振动的谐振频率与系统工作频率的偏差小于20Hz。

2.2 变幅杆的初步设计和分析

基于变幅杆一维纵向振动理论，计算出半波长矩形截面指数形变幅杆的谐振（20KHz）长度为133.2mm，所得变幅杆二维图如图1所示。

图1 半波长矩形截面指数形变幅杆二维图

采用COMSOL有限元分析软件对所设计的变幅杆进行模态分析，搜索变幅杆在系统工作频率（20KHz）附近的纵向振动的谐振频率，图2为变幅杆的纵振模态。由模态分析可知，变幅杆纵振谐振频率为19367Hz，与系统工作频率偏差较大，其主要原因是变幅杆宽度方向的尺寸大于1/4波长（62.88mm），杆的横向振动会引起谐振频率的偏移。

图2 半波长矩形截面指数形变幅杆纵振模态

借助COMSOL软件，通过调整指数形变幅杆的总长度修正其纵振谐振频率。模态分析结果显示：当指数形变幅杆总长为128.5mm时，其纵振谐振频率为19993Hz，与系统工作频率较为接近。

采用COMSOL软件对频率修正前后的变幅杆（总长133.2mm和总长128.5mm）进行谐响应分析，求解变幅杆受高频振动激励时（输入端振幅为7μm，激励频率为其纵振谐振频率，输出端无负载），输出端的纵向振动幅值沿宽度方向的分布情况，如图3所示。

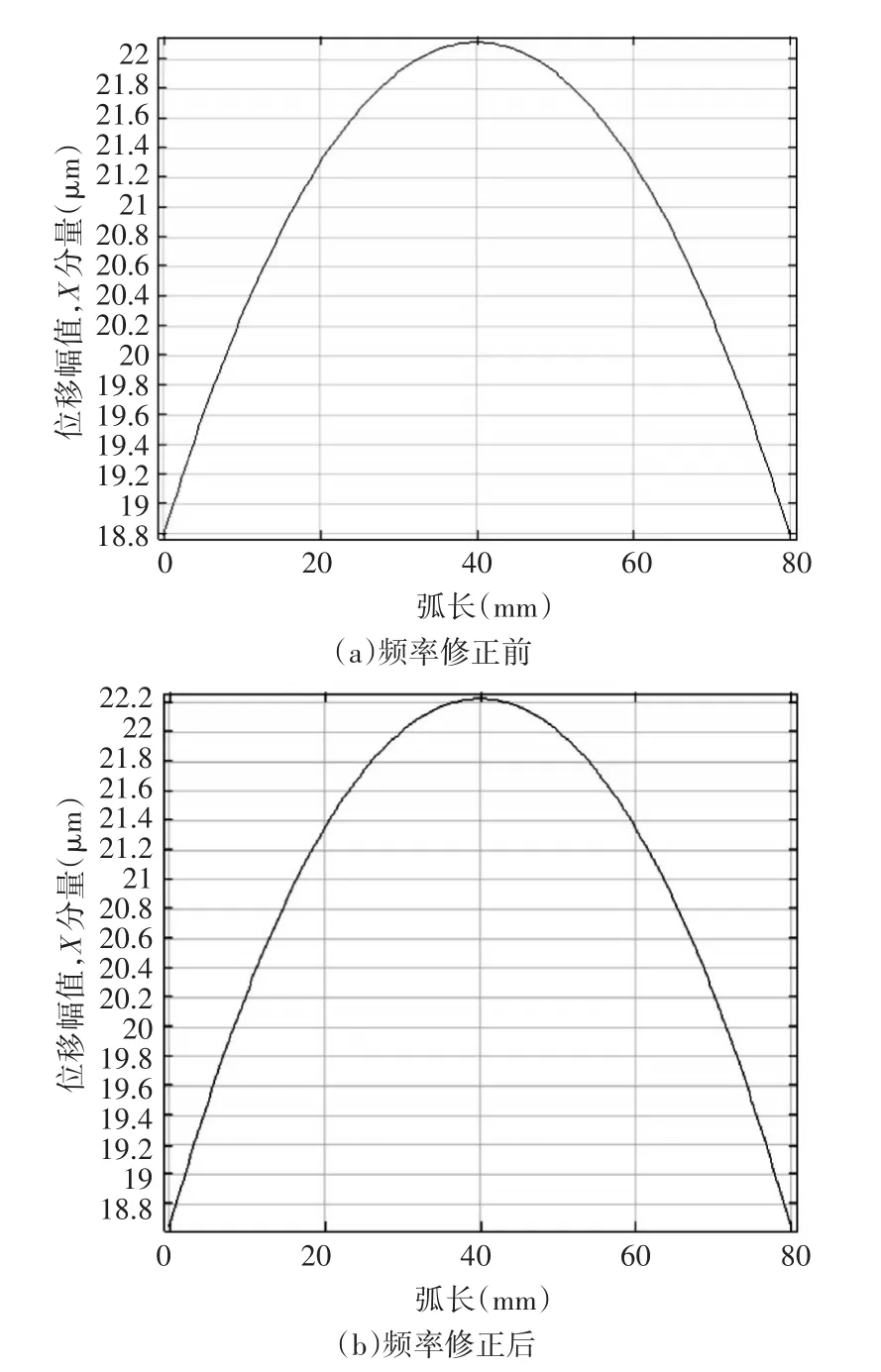
图3 变幅杆输出端位移幅值沿宽度方向的分布

由图3可知，改变变幅杆长度虽然修正了谐振频率，但是变幅杆输出端的振幅分布变化不大，即变幅杆的横向振动并没有得到抑制。因此考虑通过在变幅杆宽度方向上增加两条窄缝的方式抑制变幅杆的横向振动并修正其谐振频率。图4为增加窄缝后变幅杆的二维图。如图4所示，两条窄缝沿变幅杆中心位置对称分布，设窄缝长度为a，宽度为b，窄缝间距为d。

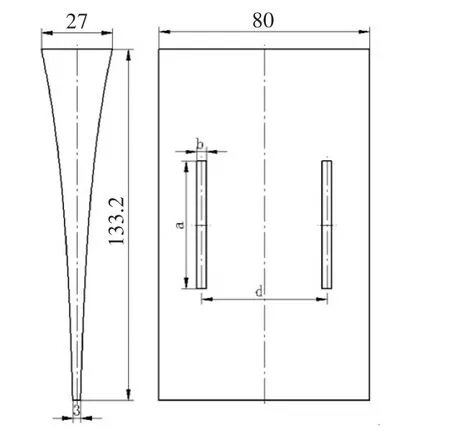
图4 半波长矩形截面指数形变幅杆（带窄缝）二维图

3 代理模型的构建及评价

3.1 代理模型理论

若要通过增加窄缝的方式将变幅杆的纵振谐振频率修正到系统工作频率附近，则需先求出变幅杆窄缝的结构参数和变幅杆纵振谐振频率之间的对应关系。然而，通过解析法直接求解较为困难。代理模型方法能够基于有限的实验数据，构建反映输入与输出关系的近似函数模型［6］。常用的代理模型方法有克里金法［7］（KRG）、多项式响应面法［8］（PRS）、支持向量回归法［9］（SVR）等。相关研究表明，针对具体的问题需要比较不同代理模型方法的建模精度才能判断该问题所适用的方法［10］。因此，需分别采用上述三种代理模型方法，建立反映窄缝结构参数与纵振谐振频率函数关系的代理模型，接着，评价建模精度并择优。

本文选用决定系数（R2）和均方根误差（RMSE）作为评价建模精度的标准：

式中，n表示验证样本数，yi表示纵振谐振频率的仿真值，表示纵振谐振频率的预测值，表示纵振谐振频率仿真值的均值。判定系数（R2）的取值范围为0～1，其用于度量模型的拟合优度，判定系数值越接近于1，说明代理模型的预测精度越高；均方根误差（RMSE）主要用于判断预测值与仿真值的误差，均方根误差值越小说明代理模型的预测精度越高。

3.2 实验设计和仿真实验

本文的设计空间即窄缝的设计变量和取值范围：40mm ≤ a≤ 100mm、0.2mm＜b≤ 8mm、20 mm＜d≤60 mm。在众多实验设计方法中，最优拉丁超立方抽样法［11～12］能够利用较少的样本点数据反映整体设计空间。本文选用最优拉丁超立方抽样法在设计空间内分别抽取30组训练样本点和15组验证样本点。

表1 样本点数据和对应的变幅杆的谐振频率

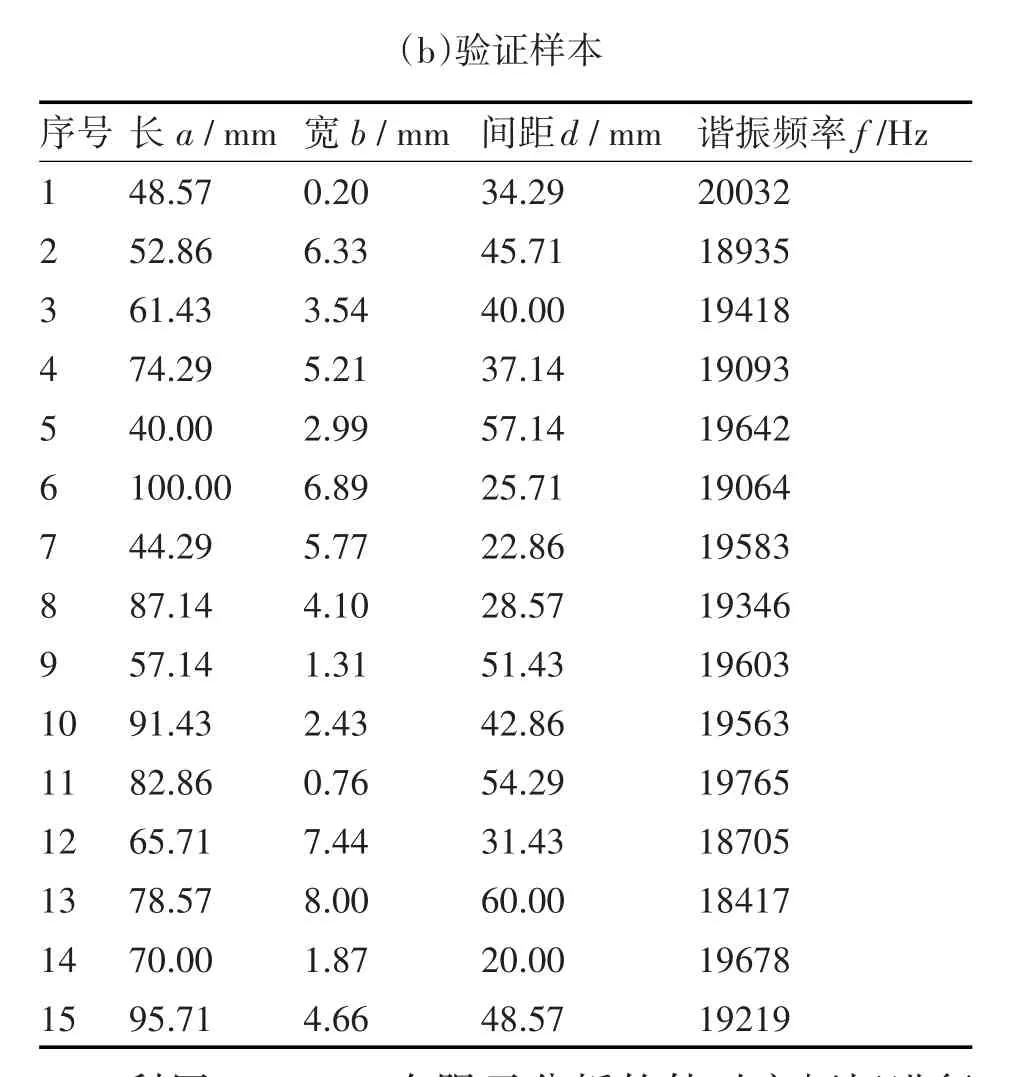
（b）验证样本谐振频率f/H z 2 0 0 3 2 1 8 9 3 5 1 9 4 1 8 1 9 0 9 3 1 9 6 4 2 1 9 0 6 4 1 9 5 8 3 1 9 3 4 6 1 9 6 0 3 1 9 5 6 3 1 9 7 6 5 1 8 7 0 5 1 8 4 1 7 1 9 6 7 8 1 9 2 1 9序号1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5长a/m m 4 8.5 7 5 2.8 6 6 1.4 3 7 4.2 9 4 0.0 0 1 0 0.0 0 4 4.2 9 8 7.1 4 5 7.1 4 9 1.4 3 8 2.8 6 6 5.7 1 7 8.5 7 7 0.0 0 9 5.7 1宽b/m m 0.2 0 6.3 3 3.5 4 5.2 1 2.9 9 6.8 9 5.7 7 4.1 0 1.3 1 2.4 3 0.7 6 7.4 4 8.0 0 1.8 7 4.6 6间距d/m m 3 4.2 9 4 5.7 1 4 0.0 0 3 7.1 4 5 7.1 4 2 5.7 1 2 2.8 6 2 8.5 7 5 1.4 3 4 2.8 6 5 4.2 9 3 1.4 3 6 0.0 0 2 0.0 0 4 8.5 7

利用COMSOL有限元分析软件对变幅杆进行模态分析，分别获取了45组样本点对应的变幅杆的纵振谐振频率。其中12、21、28号训练样本点所对应的变幅杆在15KHz～25KHz范围内未搜索到纵振模态，因此判定其无效样本点。表1为样本点数据及对应的谐振频率。

3.3 代理模型的构建及评价

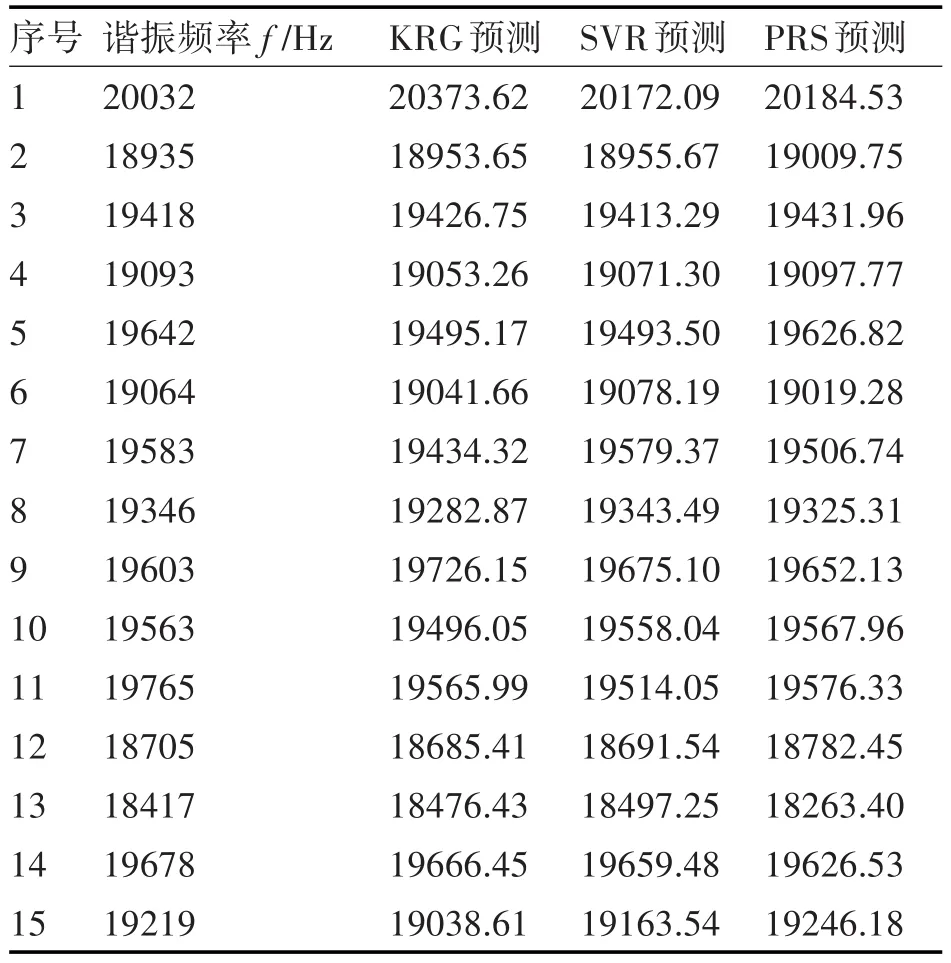
表2 变幅杆谐振频率的仿真值和三种代理模型的预测值

本文中预测变幅杆谐振频率的模型是利用Matlab中的代理模型工具箱SRGTS Toolbox构建的。选取表1（a）中的27组有效训练样本作为训练数据，采用三种代理模型方法构建根据变幅杆结构参数预测其谐振频率的代理模型。完成建模后再取表1（b）中15组验证样本作为验证数据来验证模型的预测效果。表2为变幅杆谐振频率的仿真值和三种代理模型的预测值。

将表2数据代入式（3）、（4）中分别计算三种代理模型的预测精度结果见表3。由表3可知，PRS法构建的代理模型预测精度较高。因此选用PRS法构建的代理模型用于后续优化设计。

表3 三种代理模型对变幅杆谐振频率的预测精度

4 基于遗传算法的变幅杆优化设计

遗传算法源于达尔文的进化论、魏茨曼的物种选择学说和孟德尔的群体遗传学说。它是一种自适应全局优化搜索算法，通过循环选择、交叉、变异等步骤持续优化种群，解码末代种群的最优个体即可得到最优解［13］。本文采用遗传算法对矩形截面变幅杆的窄缝结构参数进行优化，从而实现对变幅杆纵振谐振频率的修正。算法中计算个体的适应度值所需的变幅杆谐振频率由上文PRS法构建的代理模型预测得出。遗传算法的优化流程如图5。

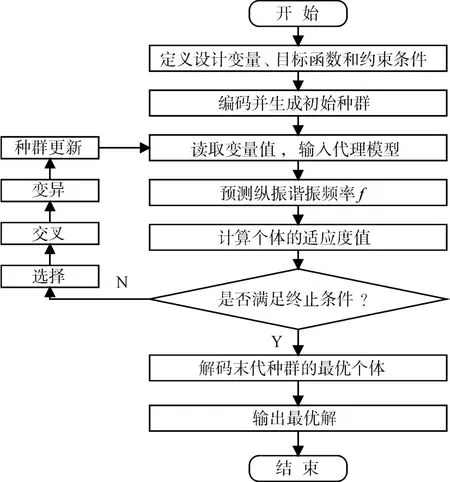
图5 结合代理模型的遗传算法优化流程图

4.1 优化模型的建立与优化求解

本文优化目标为变幅杆纵振的谐振频率与20 KHz的偏差小于20 Hz。设计变量、目标函数和约束条件如下：

式中，f是PRS法构建的代理模型对变幅杆谐振频率的预测值。在Matlab优化工具箱的遗传算法优化模块中，设定初始种群规模为200；限定遗传算法的迭代次数范围：50～99；设置选择、交叉、变异算子分别为比例选择、算术交叉、自适应变异。设置优化的终止条件为在迭代次数范围内，若适应度值的平均变化率小于0.01%则终止优化，否则迭代99次后终止。

图6为优化结果和部分优化设置。由图6可知，经过61次遗传算法迭代后得到变幅杆窄缝结构参数的最优解（保留两位小数）为a=43.04、b=0.82、d=47.87。

图6 优化结果和部分优化设置

4.2 优化结果的验证及分析

根据优化后的窄缝参数对变幅杆进行三维建模，将模型导入COMSOL Multiphysics 5.2软件进行模态分析和谐响应分析。根据模态分析结果可知：优化后，变幅杆的纵振谐振频率仅偏离系统工作频率9Hz，符合设计要求。根据谐响应分析结果可知：优化后，变幅杆输出端的纵向振动幅值沿宽度方向的分布更为均匀，即变幅杆的横向振动得到了抑制。图7为优化后变幅杆的纵振模态，图8为优化前后变幅杆的输出端的纵向振动幅值沿宽度方向的分布。

图7 优化后变幅杆纵振模态

图8 优化前后变幅杆输出端振动幅值沿宽度方向分布

5 结语

本文基于变幅杆一维纵向振动理论设计了大尺寸矩形截面指数形变幅杆，并通过增加两条窄缝的方式，在抑制变幅杆横向振动的同时修正了其纵振谐振频率。通过对设计、建模和优化的过程进行分析得出以下结论。

1）基于一维纵向振动理论设计的大尺寸矩形截面指数形变幅杆的纵振谐振频率与系统工作频率有较大偏差，仅通过调整变幅杆总长可修正其纵振谐振频率，但是变幅杆横向振动未得到抑制。

2）基于本文的样本数据，采用多项式响应面法（PRS）构建的代理模型对矩形截面变幅杆谐振频率的预测精度优于支持向量回归法（SVR）和克里金法（KRG）。

3）根据模态分析和谐响应分析结果可知：经遗传算法优化窄缝结构参数后，矩形截面变幅杆的纵振谐振频率得到了修正，且变幅杆的横向振动得到了抑制。