基于数字气象预报与动态规划的无人艇航路优选∗

李 伟 李天伟 周 兵

（1.海军大连舰艇学院航海系 大连 116018）（2.海军大连舰艇学院办公室 大连 116018）

1 引言

新世纪以来，无人艇（Unmanned Surface Vessel，USV）技术以其独特的优势受到世界各国的青睐，相继研发出性能优越的产品并大量装备部队。最近十年，世界主要军事强国继续把无人艇做大做强，使其航程和载荷出现大幅增加，能够执行越来越复杂的任务［1］。但是，随着航程的增加，航行途中的安全问题逐渐突显，海面恶劣的海况随时为形体较小的无人艇带来灭顶之灾，所以，进行航路优选以规避恶劣海况、保证无人艇的航行安全成为一个重要的研究课题。

2 需求与可行性分析

在世界范围内，美国2018年服役的“海上猎人”型反潜无人艇是典型的首款远程无人艇，该艇长约40m，自重140t，采用三体结构，最高航速可达31节，在12节的巡航速度下可连续航行10000海里［2］。“海上猎人”主要用于侦察和跟踪潜艇，装有声呐和光电传感器，能与反潜巡逻机、侦察机、反潜声呐浮标等组成传感器网络，可用于全球海域的长时间海洋监视。在性能上，虽然美军方声称该艇“能在四级海况下工作”，但是无人艇毕竟是小型海上装备，又加之其独特的三体结构，更使其大风浪航行时的稳性毫无保障，而一旦船体倾覆则造成装备尽毁，任何使命任务均无从谈起。

从公开发表的实验数据看，排水量小于50t的小型海上船舶，在四级海况以上、尤其是侧浪航行时具有极高的倾覆风险。在远海打击的情况下，无人艇从脱离母舰或基地到接近目标一般距离较远［2］，在宽阔的洋面上有多种航行路径可以选择，如果能够事先根据海洋预报信息选择相对安全的航路将能大幅提高无人艇的海上生命力，对于完成既定使命任务意义重大，而近年来蓬勃发展的数值气象预报技术使这种设想成为可能。

3 基于数字气象预报的航行安全性评估

数字气象预报，从专业角度讲就是利用各种大型气象模拟软件对特定海域海洋环境信息进行处理所得的数值预报产品，可以获得任意尺度、任意层高、任意时间（段）的温湿度、气压（差）数字信息，进而推知海区的浪高浪向、风力风向，然后据此判定无人艇航行的安全或危险指数。

浪高浪向：一般来说，在两米以下浪高时舰船航行安全有较高保障，随着浪高增大，其对舰船的破坏力和航行安全影响呈几何级数增加；顶浪或顺浪航行时舰船安全性较好，侧浪航行时危险性最大。

风力风向：风对舰船航行的影响总体弱于浪，横风时影响较大。

当温度长期极低时洋面结冰，无人艇不能破冰航行。

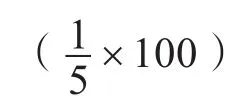
当各个航段的航行危险指数悉数求得以后，整条航路（包括多个航段）的危险指数便可累加获得，如果航路有多种可能，可用动态规划理论进行优选。整个过程可用图1表示。

图1 基于数字气象预报与动态规划的无人艇航路优选过程

4 动态规划建模分析

根据无人艇海上航渡的实际情况和动态规划的建模要求，可以把问题描述为以下几个方面［3］。

4.1 将航渡过程划分为若干个状态节点和航渡阶段

动态规划模型要求把任务的整个过程划分为n个状态节点和n-1个阶段，在这样的要求下，可以把无人艇海上远程航渡的过程分为脱离母舰、到达一岛链、到达二岛链、到达三岛链和攻击完成5个状态和接近一岛链航渡、接近二岛链航渡、接近三岛链航渡、抵近突防4个阶段。

4.2 确定状态变量

令sk为第k(k=n-1'n-2'…1)个阶段开始时无人艇所处的地理坐标，则sk即为状态变量。根据问题实际，除了首尾2个状态以外，其余状态均有可能有多种选择（本例中即为某岛链上不同的海峡水道），状态变量的集合即为此状态所有可能的选择，用Ak表示。

4.3 确定每阶段的允许决策集合和决策变量

允许决策集合Dk(sk)即为在状态sk时向下一状态推进时可以选择的不同地理坐标，显然，有Dk(sk)⊆Ak+1。决策变量xk(sk)表示在sk位置上时做出的选择，同时也成为下一阶段的初始状态。

4.4 状态转移方程

本例所指状态变量是离散的且是确定性的，故状态转移方程sk+1=xk(sk)。

4.5 指标函数、最优指标函数与递推方程

设Vkn表示指标函数，则：

其中，dj(sj'sj+1)即为从sj到sj+1的航段危险指数。每一个航段的危险指数在形式上都可以表示为浪高浪向因子w、风速风向因子g、海区温湿度因子m等的函数，故定义

最优指标函数fk(sk)表示在第k阶段处于sk位置上，采用最优航路完成航渡的最小危险指数。

递推方程为：

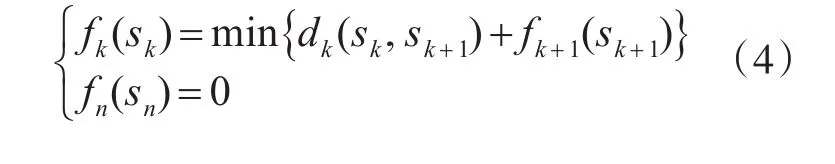
5 算例

假设某无人艇需要横跨三道岛链才能最终接敌完成特定任务，从离开母舰（A）开始，在第一岛链有3种航门水道可选（B1、B2、B3）、在第二岛链有2种航门水道可选（C1、C2），在第三岛链有3种航门水道可选（D1、D2、D3），最终从第三岛链上某处抵近攻击（E），任意两个相邻状态之间的危险指数经测算并标于状态之间的连线之上。

动态规划路线图如图2所示。

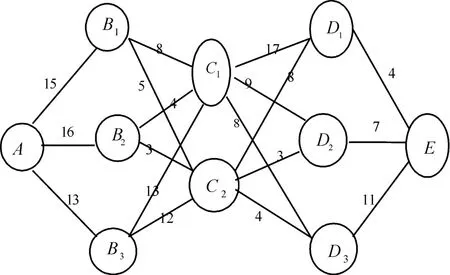
图2 动态规划路线示意图

下面按照递推方程示范优选过程。

1）从第三岛链至攻击完成阶段。

当k=4时，因s4可取D1、D2、D3三种状态，应分别计算。

所以x4(D1)=E，最安全路线为D1→E。

同理，f4(D2)=7，x4(D2)=E，当前最安全路线为D2→E。

f4(D3)=11，x4(D3)=E，当前最安全路线为D3→E。

2）从第二岛链至第三岛链阶段。

当k=3时，因s3可取C1、C2两种状态，应分别计算。

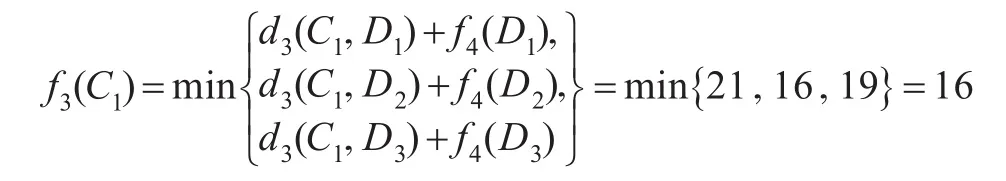
所以x3(C1)=D2，当前最安全路线为C1→D2。

同理，f3(C2)=min{12'10'15}=10，所以，x3(C2)=D2，当前最安全路线为C2→D2。

3）从第一岛链至第二岛链阶段。

当k=2时，因s2可取B1、B2、B3三种状态，应分别计算。

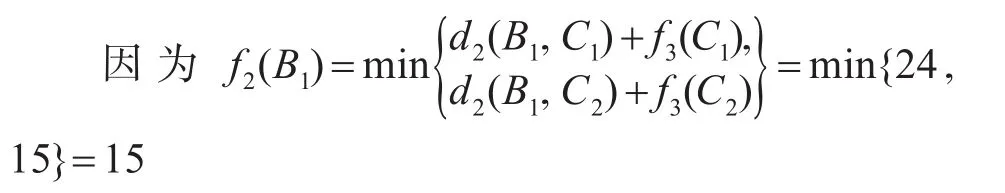
所以x2(B1)=C2，当前最安全路线为B1→C2。

同理，f2(B2)=min{20'13}=13，x2(B2)=C2，当前最安全路线为B2→C2。

f2(B3)=min{29'22}=22，x2(B3)=C2，当前最安全路线为B3→C2。

4）脱离母舰至第一岛链阶段。

当k=1时，s1只有A一种状态，故

所以x1(A)=B2，当前最安全路线为A→B2。

综上，逆向推导可得最佳航路为A→B2→C2→D2→E，最低危险系数为29。

6 结语

基于数字气象预报和动态规划的航路优选办法能够为无人艇优选一条最平稳的航路，具有计算速度快、易编程、易扩展等优点，是海面无人装备航路设计的有益参考［4］。在无人艇远程航渡接敌阶段，航行安全是最大的安全，只要能够安全接近目标，就能实施侦察或有效消耗敌方作战资源，为己方其他方面作战赢得主动［5］。航路规划是未来无人艇智能化的重要一环，它能够显著提高无人装备的海上生命力，对于装备发展具有重要意义。