基于改进量测划分策略的概率假设密度滤波器∗

（商丘职业技术学院机电系 商丘 476000）

1 引言

概率假设密度（Probability Hypothesis Density，PHD）［1］滤波器克服了传统目标算法中的数据关联困难，近年来引起了目标跟踪领域学者的广泛兴趣。高斯混合PHD（GaussianmixturePHD，GM-PHD）滤波器［2］是PHD滤波器的一种解析式。GM-PHD滤波器能够稳定地从目标后验强度中抽取目标状态估计，被广泛应用于多目标跟踪领域［3～5］。

目标跟踪场景中的杂波强度对多目标滤波器的滤波性能具有较强的干扰［6～8］。基于一个经验门阈值的量测门技术，文献［9］提出一种量测驱动的多Bernoulli（MD-Bernoulli）［10］滤波算法。MD-Ber⁃noulli滤波器首先利用测量驱动方法将每一时刻量测集划分为杂波集和目标量测集，然后使用目标量测集更新目标预测强度。与PHD滤波器相比，MD-Bernoulli滤波器的计算负担相对更小。同样基于经验门阈值的量测门技术，PHD滤波框架下文献［11］提出一种量测驱动新生目标强度估计算法。该算法避免了利用每一时间步量测集中的所有量测来建模新生目标强度，从而有效地提高了标准GM-PHD算法的计算效率。文献［12］提出一种最近邻量测驱动的GM-PHD（NMD-GM-PHD）滤波器。该算法首先为每个目标选择一个距离最近的量测，然后基于这些目标量测构建用于目标预测更新所用的新的量测集。与GM-PHD滤波器相比，NMD-GM-PHD滤波器不仅具有较高的目标状态估计精度，而且其计算效率得以较大的提升。

本文提出一种基于改进量测划分策略的概率假设密度（IMPS-GM-PHD）滤波器。通过利用一个与目标权重相关的非经验门阈值的量测门方法，IMPS-GM-PHD滤波器能够有效地从量测集中选择目标的真实量测，且一定程度上避免了由经验门阈值的量测门技术导致的量测漏选问题。

2 GM-PHD滤波器

PHD滤波器通过迭代传递目标强度实现多目标状态及数目估计。由于PHD滤波器更新步中含有集合积分运算，因此该滤波难以计算闭合解。线性高斯噪声系统中，GM-PHD滤波器利用一定数量的高斯分量的加权和近似目标强度。GM-PHD滤波器主要由预测步和更新步组成［2］。

预测步：k-1时刻，假设目标后验强度由Jk个高斯分量的混合表示为

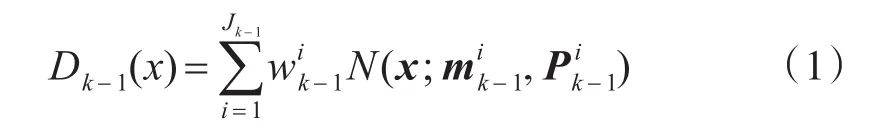
其中为N(·)一个高斯密度。则k时刻目标预测强度的高斯混合为

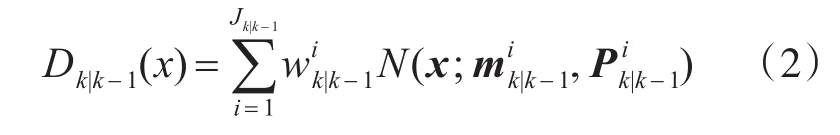
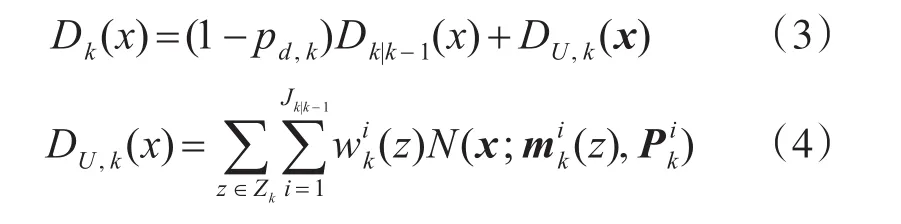
其中pd'k为检测概率。

3 IMPS-GM-PHD滤波器

3.1 改进的量测划分方法

由式（3）可知目标后验强度Dk(x)由两个目标强度构成。第一部分为由检测概率因素表示可能的目标漏检强度；第二部分为目标预测强度Dk|k-1(x)经更新后得到的目标后验强度。式（3）右侧的第二项常规更新项中，目标预测强度Dk|k-1(x)的更新是基于该时刻量测集Zk中的所有量测。由于受杂波干扰，式（3）左侧的目标后验强度并不精确，因此，目标状态及数目将难以正确地估计。

量测门技术是一种建立目标与其对应量测间关联的方法，已被应用多目标跟踪领域［13］。现有的多目标跟踪滤波器采用的量测门技术基本上都是基于固定经验门阈值的量测门方法。该类方法的不足为门阈值的大小通常难以正确设定，且一个不合理的门阈值将导致目标强度难以被正确更新。基于固定经验门阈值的量测门技术，本文提出一种改进的量测划分方法。该方法将目标权重与固定经验门阈值进行融合，充分体现了最能代表目标重要程度的权重参数在目标-量测关联中的作用。改进的量测划分方法能够有效地从量测集中选择目标的真实量测，且一定程度上避免了由经验门阈值的量测门技术导致的量测漏选问题。

其中Hk为量测矩阵，Rk为量测噪声协方差矩阵。

从量测集Zk中抽取目标量测集Ztar'k后，杂波量测集Zclu'k可表示为

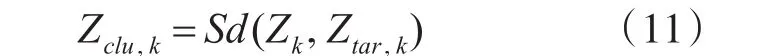
其中Sd(Zk'Ztar'k)表示求集合Zk与集合Ztar'k的差集。

3.2IMPS-GM-PHD滤波器的核心步骤

预测步：k时刻，目标预测强度由式（2）表示，其中第i个高斯分量的权重、均值及协方差分别为

其中ps'k为存活概率、Fk-1为目标状态转移矩阵、Qk-1为目标状态噪声协方差，和分别为k-1时刻第i个高斯分量的权重、均值和协方差。

量测划分步：基于3.1改进的量测划分方法，划分k时刻量测集Zk，生成目标量测集Ztar'k和杂波量测集Zclu'k。

更新步：基于目标预测强度Dk|k-1(x)和目标量测集Ztar'k，目标后验强度Dk(x)为

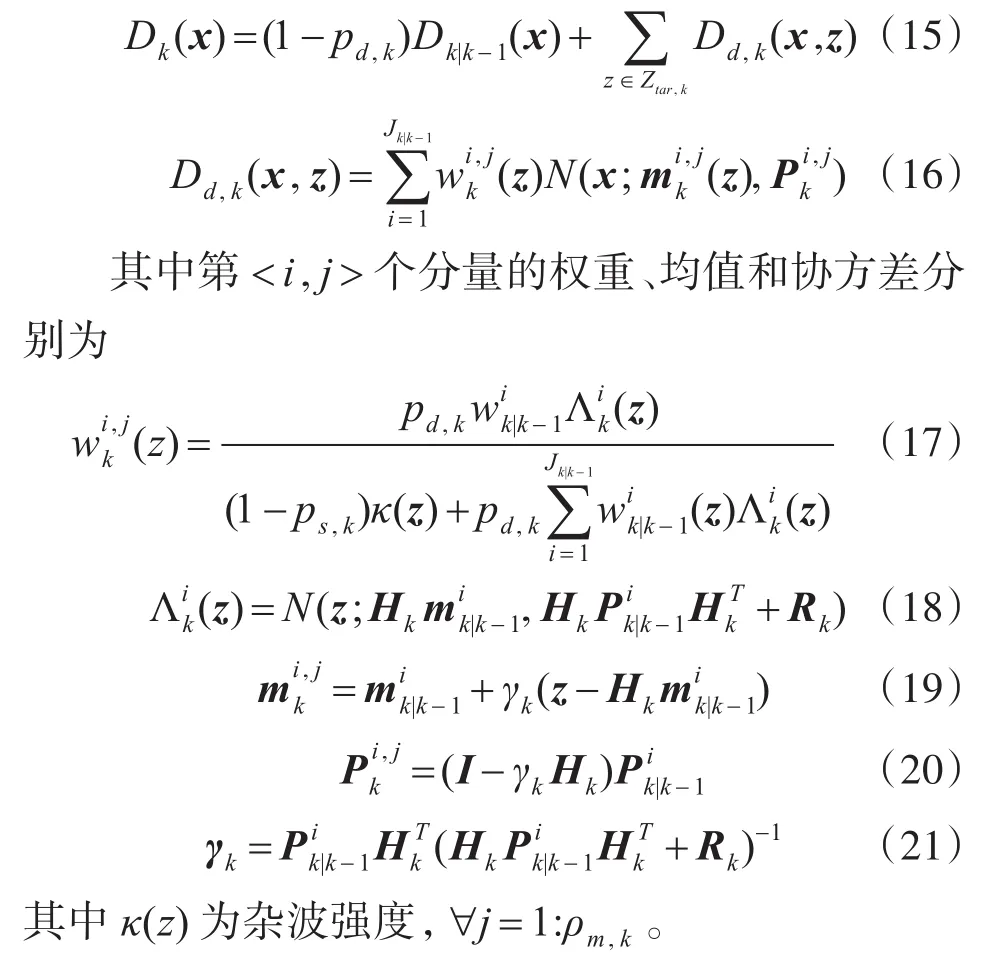
4 实验结果与分析

图1给出了一个二维区域内目标轨迹及量测的仿真，其中杂波均值为15、检测概率为0.99和存活概率为0.98。基于OSPA距离［14］和运算时间两个性能指标，IMPS-GM-PHD滤波器分别与GM-PHD、MD-GM-Bernoulli和 NMD-GM-PHD 滤波器进行对比。

图1 多目标跟踪仿真场景

图2给出了四个多目标滤波器的OSPA距离和运算时间对比。可见，GM-PHD滤波器不仅OSPA距离相对最大，而且运算时间相对也最高。这表明GM-PHD滤波器的目标状态估计精度较低。与GM-PHD滤波器相比，MD-GM-Bernoulli、NMD-GM-PHD和IMPS-GM-PHD滤波器均取得相对较小的OSPA距离和较低的运算时间。尤其是，IMPS-GM-PHD滤波器在保持较低的运算时间的同时，取得了最小的OSPA距离。

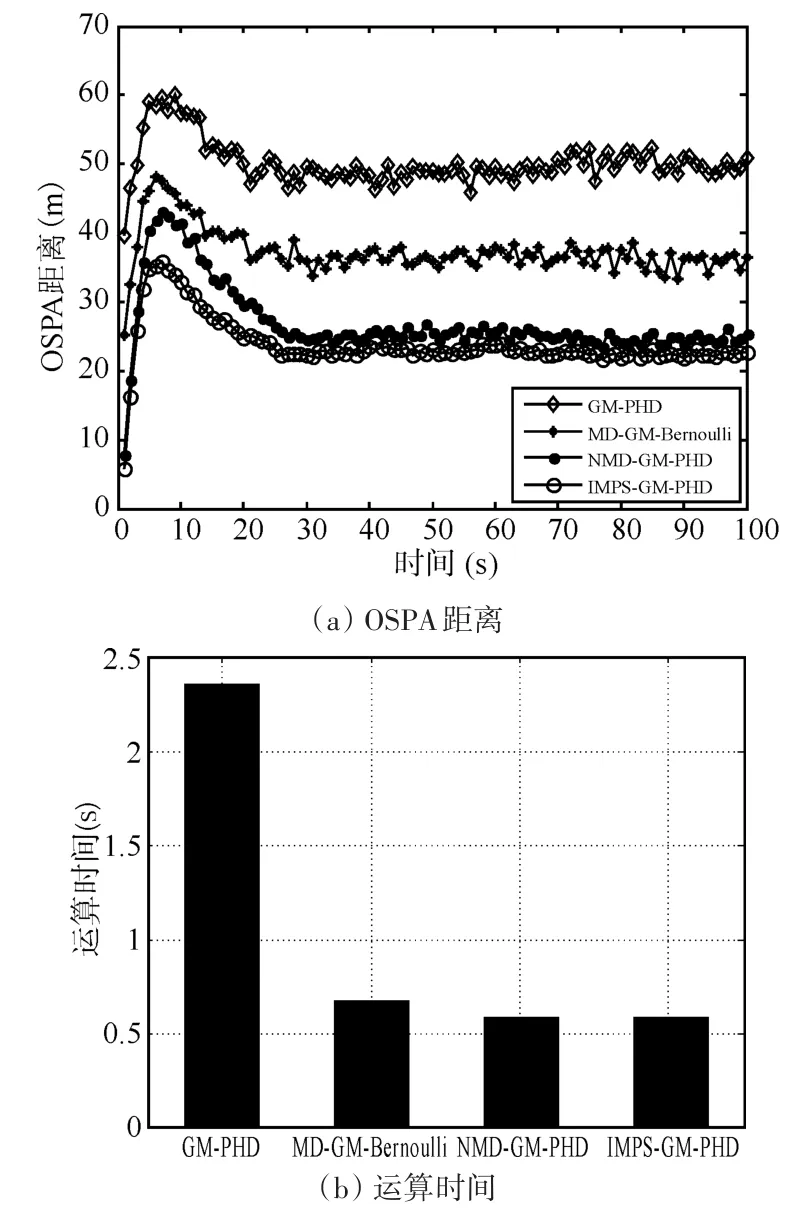
图2 四个多目标滤波器的性能对比

图3给了 GM-PHD、MD-GM-Bernoulli、NMDGM-PHD和IMPS-GM-PHD滤波器在不同杂波数目下的性能对比。随着杂波均值的逐渐增大，GM-PHD和MD-GM-Bernoulli滤波器的OSPA距离也逐渐增大。然而，NMD-GM-PHD和IMPSGM-PHD滤波器的OSPA距离并没有随杂波均值的增大而改变。此外，IMPS-GM-PHD滤波器的OSPA在各杂波均值处均相对最低。同时，GM-PHD滤波器运算时间同样随着杂波均值的增大而不断增多。然而，MD-GM-Bernoulli、NMDGM-PHD和IMPS-GM-PHD滤波器的运算时间在各杂波均值处基本维持不变。

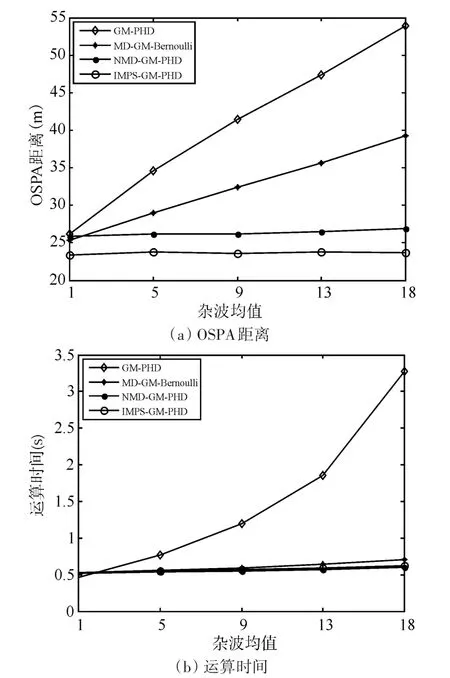
图3 不同杂波均值下四个多目标滤波器的性能对比

5 结语

针对密集杂波场景下标准PHD滤波器的计算负担大及滤波精度低等问题，通过对基于经验门阈值的量测门技术的改进，本文提出一种IMPS-GMPHD滤波器。该滤波器首先将表示目标重要程度的权重参数与经验门阈值进行融合得到一个融合阈值，然后使用该融合阈值作为目标量测划分的门阈值对各时刻量测集进行划分，最后采用从量测集中抽取的目标真实量测来更新目标预测强度。实验结果表明，IMPS-GM-PHD滤波器具有较高的目标状态估计精度和较低的运算时间。未来将研究基于多传感器的GM-PHD滤波器在群目标跟踪中的应用。